В прямолинейном канале при очень малой скорости потока отдельные струи движутся параллельно друг другу, без видимого обмена жидкостью, содержащейся в них. Такое упорядоченное установившееся движение называется ламинарным (или струйчатым). В ламинарном потоке скорость в каждой точке со временем не меняется.
В ламинарном потоке скорость по сечению распределена по параболическому закону, у стенки канала она равна нулю. Средняя скорость по сечению канала составляет половину максимальной скорости.
При увеличении скорости потока параллельное движение струек нарушается, их пути становятся неправильными, извилистыми и, наконец, струйки распадаются на отдельные элементарные объемы жидкости— моли. Последние независимо одна от другой увлекаются беспорядочными движениями и перемещаются по индивидуальным неправильным криволинейным траекториям. В результате беспорядочного движения частиц происходит интенсивное перемешивание жидкости. Такое неупорядоченное неустановившееся движение называется турбулентным.
В частности, в случае движения одного слоя жидкости вдоль другого при наличии поперечного градиента скорости появляются возмущения, приводящие при достаточно больших числах Ке к возникновению турбулентности. Граница раздела между ними неустойчива. В этой области возникает вихревое движение, превращающее первоначально равномерное движение в хаотическое. Вдоль по течению область распространения хаотического движения расширяется.
В процессах горения важное значение имеет турбулентное движение.
В турбулентном течении благодаря интенсивному перемешиванию жидкости скорость по сечению распределяется более равномерно, средняя скорость по сечению канала составляет 80—85% максимальной скорости. Наибольший градиент скорости наблюдается около стенки в очень тонком пограничном слое, толщина которого уменьшается с увеличением скорости течения.
Таким образом, турбулентное движение можно представить как беспорядочное движение отдельны^ молей жидкости. По размерам моли жидкости могут быть от самых больших, соизмеримых с поперечными размерами потока, до самых малых. Моли постоянно возникают и исчезают, существуя как индивидуальные образования ограниченное время. В результате непрерывного беспорядочного передвижения молей жидкости в каждой точке турбулентного потока скорость во времени изменяется по величине и по направлению нерегулярно, колеблясь около некоторого среднего значения. Пульсирует и поле давлений.
Отклонение значения истинной скорости от средней по времени
И-Ю = и’ (6-10)
Называется пульсационной скоростью.
Пульсационная скорость непрерывно изменяется и по величине, и по направлению. По абсолютной величине £/’ преимущественно меньше средней скорости, она доходит до ±30% О и более. Пульсационная скорость по направлению одинаково часто меняется вдоль и поперек потока и может быть положительной и отрицательной. Среднее значение пульсационной скорости за достаточно большой промежуток времени по определению равно нулю.
Движение жидкости в турбулентной области неустановившееся. Если осредненные величины скоростей и напряжений остаются постоянными во времени, то такое движение называют установившимся пуль- сационным или в среднем установившимся движением.
Несмотря на совершенно произвольные колебания, при установившемся пульсационном движении П в каждой точке за достаточно продолжительный период времени принимает определенное значение и на — 86
Правление, характеризует собой статистический результат произвольных изменений скорости и обусловливает постоянный осредненный поток.
|
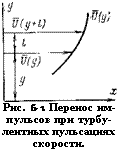
Рис. 6-1. Перенос импульсов при турбулентных пульсациях скорости. |
 В технических расчетах пользуются осредненными, среднестатистическими скоростями; истинное пульсирующее поле скоростей заменяется осредненным прямолинейным движением и ‘рассматривается распределение осредненных скоростей.
В технических расчетах пользуются осредненными, среднестатистическими скоростями; истинное пульсирующее поле скоростей заменяется осредненным прямолинейным движением и ‘рассматривается распределение осредненных скоростей.
Рассматривая плоский равномерный поток с осью х, направленной вдоль движения, можно осредненную скорость выразить в зависимости от ординаты у (рис. 6-1). Можно представить, что в таком потоке отдельные слои двигаются параллельно друг другу с осредненной скоростью.
Частица (моль) газа, имеющая в данном месте скорость и, проскакивая поперек потока отрезок, равный длине пути смешения, попадает в слой, где значение средней скорости отличается от П на величину:
Йу
В формуле:
/т — длина пути смешения;
Йи]йу — местный градиент скорости.
Слияние этой частицы с массой нового слоя сопровождается скачкообразным изменением, т. е. пульсацией скорости на величину
У’ = Д£/ = /1-^.. (6-12)
Следовательно, продольная пульсационная скорость есть не что иное, как относительная скорость, которую имеют частицы, попадающие из области одной скорости в область другой.
Применение принципа неразрывности к элементарному объему позволяет установить связь между осевым и поперечным компонентами пульсационной скорости. Из неизменности массы следует предположение о том, что пульсирующие течения в осевом и поперечном направлениях должны компенсировать друг друга, и, следовательно, в среднем осевые и поперечные компоненты пульсационной скорости должны быть одного порядка.
Таким образом, механизм турбулентности представляется в некоторой степени аналогичным механизму молекулярного движения. Различие заключается в том, что во втором случае перемешивание происходит в результате беспорядочного теплового движения молекул, в случае же турбулентного движения перемешивание совершается в результате беспорядочных движений молей газа. В соответствии с этой аналогией введено понятие длины пути смешения, имеющее для турбулентного движения такой же смысл, как понятие о средней длине пробега молекул в кинетической теории газов. Длина пути смешения есть расстояние, на которое перемещаются моли газа некоторого слоя до внедрения их в другой, или, другими словами, это путь, на протяжении которого частица сохраняет свою индивидуальность, т. е. движущийся моль газа проходит это расстояние, не распадаясь. В частности, это некоторая средняя поперечная длина, пройдя которую отдельные, перемещающиеся в потоке моли жидкости теряют свою
Скорость и приобретают скорость окружающей среды. Обычно величина, масштаба свободной турбулентности составляет некоторую долю меньшего размера потока.
Длина пути смешения по порядку совпадает с поперечным размером моля, движущегося в течение данного отрезка времени как единое целое, поэтому его можно представлять так же и как средний диаметр жидкого комка или вихря, а следовательно, как некоторый характерный масштаб турбулентности в данной точке потока. Следовательно, масштабом турбулентности является также осредненное значение длины пути смешения как величина, характерная для процесса турбулентного — перемешивания.
В непрерывной среде, состоящей из бесконечно большого числа частиц и обладающей исключительной подвижностью, сила тяжести и скорость турбулизируют поток. Наоборот, вязкость уменьшает подвижность частиц и тем самым действует как стабилизирующий фактор. Поэтому отношение сил инерции, к которым относится сила тяжести и сила, соответствующая кинетической энергии, к силам вязкости характеризует степень турбулентности потока.
Это отношение называют критерием Рейнольдса
= (6-13>
[XV у
В формуле:
Р — плотность среды, кг/м3;
XV — средняя скорость потока, м/с;
(і — коэффициент динамической вязкости, н-с/м2;
V — коэффициент кинематической вязкости, м2/с;
/—линейный параметр, характеризующий форму поперечного сечения потока, м.
Наличие стенок ограничивает свободу движения частиц и тем самым стабилизирует поток, поэтому в выражение критерия Рейнольдса входит также линейный параметр, характеризующий форму поперечного сечения потока.
Повышенное значение критерия Рейнольдса указывает на большую степень турбулентности. Экспериментально было установлено, что при значениях 1^е<1^екр=:::2320 в трубах и каналах движение имеет ламинарный характер, а при Ке>^екр—турбулентный. При значениях Ие значительно выше критического молекулярная вязкость перестает играть заметную роль, наступает область развитой турбулентности. Все выше сказанное о механизме турбулентного движения относится, к области развитой турбулентности, когда эффектом молекулярной диффузии и теплопроводности можно пренебречь по сравнению с турбулентным массо — и теплообменом.
Степень турбулентности
Колебания скорости в каждой точке турбулентного потока происходят вокруг некоторого среднего ее значения. Поэтому средняя скорость является одной из основных ^характеристик пульсирующей скорости.
Так как среднее значение пульсационной скорости равняется нулю,, то для оценки величины амплитуды отклонений истинной скорости от средней введено понятие среднего квадратичного отклонения пульсационной скорости Оц— YU’ * •
Величина ои Дает меру рассеяния случайной величины и является •основной характеристикой амплитуды пульсации скорости в фиксированной точке. Среднее значение квадрата пульсационной скорости за некоторый промежуток времени определяется следующим образом:
*
17^=— ^{и-йуМ, (6-14)
О
Где t — период осреднения.
Средние квадратичные отклонения двух других проекций скорости соответственно определяются как
0>,= |/’Р"и оа7 = 1/Р?. (6-15)
Таким образом, для характеристики пульсирующей скорости необходимо знать средние значения трех проекций скорости и средние квадратичные значения проекций пульсационной скорости.
Отношение средней квадратичной пульсационной скорости, принимаемой за меру пульсационной скорости, к средней скорости
£==Л^1 (6-16)
И
•называется интенсивностью или степенью турбулентности. Это отношение также называют числом Кармана. Критерий е выражает отношение дополнительных турбулентных напряжений к силам инерции и является первой характеристикой турбулентности.
Пульсации скоростей в различных точках связаны между собой статистическими связями. Основной количественной мерой связи между статистическими явлениями в теории вероятностей является коэффициент корреляции (связи)—отношение среднего значения произведения пульсационныд скоростей к произведению их средних квад
Ратичных значений.
Коэффициент корреляции между скоростями пульсации и и V’г •в двух точках осредненного плоского потока с основным направлением течения по х, находящихся одна от другой по оси у на расстоянии т) =
— У2—#1 в один и тот же момент времени,
К, = 77^77=- (6-17)
Корреляция пульсационных скоростей в точках, близких друг тс другу, большая. При совпадении сравниваемых точек коэффициент корреляции между одноименными проекциями скорости равен единице, Т. е. При Г|=0 #, = 1.
С увеличением расстояния взаимозависимость пульсаций в этих точках ослабляется, так как эффективное влияние турбулентных возмущений распространяется на весьма малую область. Если расстояние между рассматриваемыми точками велико по сравнению с турбулентными перемещениями, то связь между пульсационными скоростями теряет функциональный характер, они становятся почти независимыми и поэтому осредненное значение их произведения становится равным нулю, т. е. при Т]—*оо ^=0.
Уменьшение корреляции с расстоянием означает, что закономерная связь между гидродинамическими величинами имеется в бесконечно малых объемах потока, для которых коэффициент корреляции между скоростями в двух точках равен единице. При конечных расстояниях связь между этими величинами теряет функциональный характер. С увеличением числа Ие коэффициент корреляции возрастает.
Распределение коэффициента корреляции в пространстве позволяет оценить границы областей возмущений, средние размеры этих областей, т. е. найти средний масштаб турбулентности.
Линейная величина
(6-18)
Представляет собой среднее расстояние, на которое распространяется корреляционная связь скорости в данной точке со скоростями в другие точках и поэтому является некоторым средним размером масс жидкости, формирующих поток, и характеризует средний эффективный размер перемешивающихся молей. Эта величина называется эйлеровым поперечным масштабом турбулентности.
Величина масштаба турбулентности является второй статистической характеристикой турбулентного потока и дает представление о пространственной структуре турбулентных возмущений, характеризует размеры больших вихрей в турбулентном потоке.
|
О |
![]()
![]() Можно составить коэффициент корреляции также и для точек, лежащих на оси х на расстоянии ^ = х2—х± одна от другой, и соответственно вычислить продольный эйлеров масштаб турбулентности:
Можно составить коэффициент корреляции также и для точек, лежащих на оси х на расстоянии ^ = х2—х± одна от другой, и соответственно вычислить продольный эйлеров масштаб турбулентности:
И’,и’‘ с£. (6-19)
Коэффициент корреляции между двумя составляющими пульсаци- онной скорости в одной и той же точке
К = — Г^У — — (6-20)
У И’,2
Характеризует величину дополнительных турбулентных напряжений.
Корреляция одного и того же компонента в данной точке в разные моменты времени позволяет определить эйлеров макромасштаб времени для данной оси:
Г1£=]к1£(()<к, (6-21)
0
Где
И’2
|
И’. |
Эйлеров макромасштаб времени представляет собой время, в те-
Е
Чение которого крупные моли со средней скоростью О проносятся через фиксированную точку пространства.
При однородной турбулентности осциллограмма мгновенной скорости, снимаемая в данной точке потока по времени, практически идентична мгновенному распределению скорости по направлению потока (ось х), поэтому коэффициенты корреляции /?, и Ях тождественно
Равны друг другу при наличии связи х—ТЛ.
Соответственно
Ь .
ХЕ хЕ
Если некоторая частица жидкости в момент 4 прошла через заданную точку потока, имея скорость II'({о), ТО В момент (А) + ^) ее скорость
Составляет £/'(£0 + ^) и лагранжев коэффициент корреля
Ции по оси I равен:
$ _ (М У’г’ (и 0 22)
Соответственно лагранжев макромасштаб времени:
СО
^ (6-23)
О
.а лагранжев макромасштаб длины, являющийся макромасштабом вихревой диффузии:
(6-24)
Лагранжев масштаб длины Ь. характеризует расстояние, на которое
Перемещаются моли, сохраняя свою индивидуальность, а лагранжев
Макромасштаб времени I. — время, в течение которого моль проходит
Это расстояние.
Частота пульсаций
За средний период пульсации принимается отношение і/М, где N — число максимумов или минимумов мгновенной скорости за период осреднения І.
Величина, обратная периоду пульсации,
“= -7-. (6-25)
Показывающая число пульсаций скорости в данной точке за секунду, называется частотой пульсаций.
Частота пульсаций скорости является третьей основной характеристикой турбулентности. В турбулентных потоках наблюдаются широкие спектры частот. Поэтому за меру частоты пульсаций принимают либо частоту, более всех повторяющуюся, либо некоторую среднюю частоту. Различают низкочастотную (крупномасштабную) и высокочастотную (мелкомасштабную) турбулентность.



 9 апреля, 2013
9 апреля, 2013  doctype
doctype  Опубликовано в рубрике
Опубликовано в рубрике