Как было ранее сказано, при нормальном распространении пламени фронт пламени (зона горения) имеет малую толщину и делит массу газа на две части; впереди него находится слабонагретая горючая смесь, позади — сильно нагретые продукты сгорания. Из-за этого в пламени происходят энергичные процессы диффузии. Поэтому передача тепла от фронта пламени прилежащим слоям смеси совершается не только за счет молекулярной теплопроводности, но и за счет диффузии продуктов сгорания в исходную смесь, которая сопровождается одновременным отводом некоторой части этой смеси в зону горения. Диффузия продуктов сгорания вызывает такой же нагрев смеси, какой получился бы, если бы это же количество продуктов сгорания образовалось в результате химической реакции. В процессе диффузии из зоны горения в свежую смесь проникают также промежуточные активные продукты: атомарный водород и кислород, гидроксильные радикалы ОН и другие нестойкие соединения, получаемые в ходе реакции.
В зоне горения температура изменяется от начальной температуры исходной смеси Г0 до температуры горения Гг, причем одновременно изменяется и концентрация реагирующих веществ. Химические реакции происходят при всех температурах в этом интервале, но с различной скоростью. Скорость реакции экспоненциально увеличивается с ростом температуры, но так как одновременно с повышением температуры концентрация исходной газовой смеси падает, то скорость химической реакции достигает максимума при температуре несколько ниже температуры горения. Чем больше скорость химической реакции, тем больше скорость распространения пламени и меньше время пребывания газа в зоне горения. Для протекания реакции при высокой температуре этого времени достаточно, тогда как в интервале низких температур прореагирует лишь незначительная часть смеси. Основная часть исходной смеси реагирует при температурах, близких к температуре горения, и поэтому скорость распространения пламени должна соответствовать ей. Следовательно, в пламени химические реакции протекают в основном в малом интервале температур А Г, близком к температуре горения, в смеси, сильно разбавленной продуктами сгорания [Л. 19, 20].
Таким образом, распространение пламени связано с химическим реагированием, сопровождающимся расходом исходных веществ и вы- 128
делением тепла в среде, в которой имеет также место перенос тепла теплопроводностью и вещества—диффузией.
Поэтому для изучения процесса распространения пламени необходимо одновременно рассматривать уравнение теплопроводности и диффузии. Для простоты изложения рассмотрим случай установившегося режима горения в системе координат, связанной с пламенем. Если при этом будет рассматриваться случай распространения пламени в неподвижном газе, то система координат будет движущейся в пространстве. В случае же, когда газ продувается сквозь стационарное пламя, она будет неподвижной. Распределение температур в выбранной системе координат в обоих случаях будет стационарным.
|
Рис. 8-5. Распределение температуры и концентрации в пламени. Т — изменение температуры; С — концентрации горючей смеси; ИР —скорости реакции. |
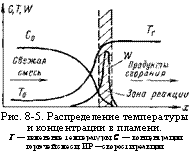 Так как толщина зоны горения мала по сравнению с кривизной поверхности фронта пламени, можно считать, что температура и состав газа внутри зоны горения являются функциями одной координаты, перпендикулярной элементу пламени. На рис. 8-5 показано распределение температуры и концентрации, а также изменение скорости реакции в пламени.
Так как толщина зоны горения мала по сравнению с кривизной поверхности фронта пламени, можно считать, что температура и состав газа внутри зоны горения являются функциями одной координаты, перпендикулярной элементу пламени. На рис. 8-5 показано распределение температуры и концентрации, а также изменение скорости реакции в пламени.
Эти зависимости имеют форму плавных, но резко изменяющихся кривых. На большей части зоны горения происходит нагрев смеси, а химическая реакция протекает на незначительной ее длине, в малом интервале температур, примыкающем к температуре горения.
Выделим в зоне горения элементарный слой йх и составим для него уравнение теплового баланса, отнесенное к единице сечения потока и единице времени. При установившемся режиме горения в элементарном слое выделяется тепла в количестве:
ЙС1Р = Ф(Т, С)ёх. (8-18)
При отсутствии теплопотерь часть этого тепла расходуется на нагрев реагирующей смеси, а остальная часть отводится из слоя теплопроводностью. На нагрев смеси тепло расходуется в следующем количестве:
|
С1Т |
|
ИрСр-^ёх. (8-19) |
|
■Т + £._Т |
|
(КЗ. л — ирСрТ^+ах — ирСрТ х — и? С[ |
В формуле (8-19):
Ф(Т, С) —объемная скорость тепловыделения, кВт/м3; и, р, ср и Г— соответственно скорость движения газов, м/с, плотность смеси, кг/м3, теплоемкость, кДж/(кг-К), и температура в рассматриваемом сечении.
•
|
11 * йГ, —-г— Я — т— ах, ах ах |
![]() Тепло, отводимое Из слоя за счет теплопроводности, можно определить как разность между тепловыми потоками, проходящими навстречу движению газовой смеси через плоскости х и х + (1х, отстоящие друг от друга на расстоянии йх, т. е.
Тепло, отводимое Из слоя за счет теплопроводности, можно определить как разность между тепловыми потоками, проходящими навстречу движению газовой смеси через плоскости х и х + (1х, отстоящие друг от друга на расстоянии йх, т. е.
|
СНЗт— *[37)^,,.- [~~Я0 |
![]() ‘йТ г л
‘йТ г л
Ёх
(8-20)
Х+йх |_ / X
Где % — коэффициент теплопроводности, кВт/(м • К). Напомним, что в формуле (8-19)
Ир= ипро,
Где ро — плотность исходной смеси; принято, что массовая теплоемкость реагирующего газа равна теплоемкости исходной смеси.
Приравнивая выражение (8-18) сумме (8-19) и (8-20) с учетом (8-21) и относя к единице объема, получаем уравнение теплопроводности для точки пламени, лежащей в зоне горения, в следующем виде:
В результате химического превращения и диффузии в пламени наряду с изменением температуры изменяется также и концентрация горючего вещества. Для того чтобы в уравнении (8-22) учесть зависимость тепловыделения как от температуры, так и от концентрации, необходимо совместно с уравнением теплопроводности решить уравнение диффузии.
Уравнение диффузии выражает равенство расхода вещества на реакцию ИР(Т, С)<1х общему количеству вещества, вносимого в элементарный объем конвекцией и диффузией, соответственно составляющих:
С учетом изложенного и (8-21) |уравнение диффузии может быть написано в следующем виде:
В уравнении (8-23):
С — концентрация реагирующего вещества;
№(Т, С) —объемная скорость реакции;
Э — коэффициент диффузии.
Граничные условия:
При х=—оо Т=То и С=Со]
При х = + оо Т = Тт, ^ = ^ = 0иС = 0.
Сложная зависимость интенсивности тепловыделения от Г и С создает трудности в интегрировании системы уравнений (8-22) и (8-23).
Задача о тепловом (нормальном) распространении пламени с учетом зависимости скорости реакции от температуры и концентраций реагирующих веществ была решена Я — Б. Зельдовичем и Д. А. Франк-Каменецким [Л. 19], краткое содержание этого решения заключается в следующем.
Ввиду чрезвычайно малого времени пребывания смеси в пламени можно считать, что процесс протекает адиабатически. В адиабатических условиях температура горения равна:
= ^ + (8-24)
^ Сх)
В выражении (8-24):
С0 — начальная концентрация горючего газа в смеси, кг/м3;
@ — теплота сгорания горючего газа, кДж/кг;
С-о — теплоемкость смеси, кДж/(м3*К);
Го — начальная температура смеси, К.
Си
Где С — текущая концентрация горючего газа в смеси в процессе неполного горения.
Подстановка значения Q/cv, определенного из выражения (8-24), в уравнение (8-25) после некоторых преобразований дает связь между промежуточными значениями концентрации и температуры в следующем виде:
* Г л О
При этом принято, что теплоемкость исходной смеси равна теплоемкости продуктов сгорания и пренебрегается зависимостью теплоемкости от температуры.
При равенстве коэффициента диффузии и коэффициента температуропроводности (И = а) в пламени химическая энергия распространяется с такой же скоростью, как и тепловая. Поэтому соотношение (8-26), вытекающее из закона постоянства суммы тепловой и химической энергии в процессе адиабатического горения и смешения, при условии И = а останется в силе и для условий протекания химического реагирования в пламени.
Полученное соотношение (8-26), в котором установлена связь между текущими значениями концентрации и температуры в пламени, позволяет в уравнении (8-22) интенсивность тепловыделения выразить как функцию одной только переменной температуры и перейти от системы двух дифференциальных уравнений (8-22) и (8-23) к одному в следующем виде:
Трудность решения этого уравнения связана с его нелинейностью.
Я. Б. Зельдовичем и Д. А. Франк-Каменецким уравнение (8-27) рассматривается раздельно для зоны, где реакции практически не протекают, и для зоны, где реагирует основная масса газа в малом интервале температур А Т.
В самой зоне химического реагирования скорость тепловыделения столь велика, что расходом тепла на нагрев смеси в небольшом интервале температур протекания реакций в пламени можно пренебречь и приближенно написать уравнение для зоны реакции в следующем виде:
Т. е. приближенно можно считать, что все тепло из зоны реакции теплопроводностью отводится непрореагировавшему газу.
Для интегрирования вводится новая переменная
Тогда
= (8-30)
Подстановкой выражений (8-29) и (8-30) уравнение (8-28) преобразуется к виду:
Ус1у=—ХФ (Т)йТ. (8-31)
Введенная переменная у представляет собой поток тепла, переносимого теплопроводностью через единицу поперечного сечения потока смеси, а уравнение (8-31) характеризует его зависимость от температуры.
Интегрирование уравнения (8-31) в пределах температур Гг—АТ и Гг и соответствующих тепловых потоков дает:
Гг-ДГ
В конце зоны горения вследствие окончания химического реагирования, а следовательно, и тепловыделения г/2 равняется нулю. Принимая также, что X не зависит от температуры, получаем:
1 = -|/ 21 | Ф(Т)йТ. (8-33)
1/ гГ-дг
В зоне низких температур, где реакции практически не протекают, величина Ф(Т) ничтожно мала и ею можно пренебречь и написать для этой зоны уравнение (8-27) в следующем виде:
Та же подстановка (8-29) преобразует уравнение (8-34) к виду
Йу=ипр0Срс1Т, (8-35)
Интегрирование которого в пределах температур Г0 и Гг—АТ и соответствующих тепловых потоков г/о = 0 и г/1 дает:
У1 = ипроСр[{Тг — АТ)— Т0]. (8-36)
Для установившегося процесса на границе раздела зон, т. е. в той плоскости, где Т—Тг—АТ, тепловые потоки (8-33) и (8-36) должны быть равны.
Приравнивая выражения (8-33) и (8-36) с учетом того, что АГ<С <СГг—Го, и выражение, стоящее в квадратных скобках в уравнении (8-36), приближенно принимая равным Гг—Г0, получаем:
 Проверка показала, что вычисленная по формуле (8-37) скорость распространения пламени в смеси СО с воздухом близка к значениям, полученным из опыта. Однако эта формула еще не нашла широкого применения для определения ип, так как для этого необходимо знать конкретный вид кинетического уравнения и значения констант, которые для многих реакций еще неизвестны.
Проверка показала, что вычисленная по формуле (8-37) скорость распространения пламени в смеси СО с воздухом близка к значениям, полученным из опыта. Однако эта формула еще не нашла широкого применения для определения ип, так как для этого необходимо знать конкретный вид кинетического уравнения и значения констант, которые для многих реакций еще неизвестны.
Вместе с тем теория теплового распространения щламени позволила более точно объяснить зависимость ип от состава смеси и физических параметров, в частности от температуры и давления.
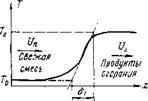
Рис. 8-6. Упрощенная схе — Основные результаты этой теории получе-
Ма структуры пламени. ны Д. А. Франк-Каменецким без интегрирова
ния дифференциального уравнения (8-27). С целью упрощения задачи он заменил истинное распределение температур во фронте пламени ломаной линией, проведя касательную к кривой действительного распределения температур в точке перегиба и продолжив ее до пересечения с прямыми, параллельными оси абсцисс и отвечающими температурам Г0 и Гг,(рис. 8-6).
Расстояние между точками пересечения 61 представляет собой ширину зоны, в которой происходит изменение температуры от Г0 до Гг и называется тепловой шириной фронта пламени.
Максимальное значение градиента температур во фронте пламени равняется:
АТ __ Тг То
В зоне разогрева, занимающей основную часть толщины пламени, химические реакции практически не протекают, поэтому поток тепла, поступающий теплопроводностью из зоны химического реагирования,
(М9)
Расходуется на нагрев поступающей в пламя горючей смеси от температуры Г0 до температуры Гг и может быть также выражен в виде
Ц = СррЦп (Гг Го), (8-40)
Где ср — теплоемкость горючей смеси при постоянном давлении; р — плотность горючей смеси.
Приравнивая выражения (8-39) и (8-40), получаем уравнение для нормальной скорости распространения пламени:
Где 1к/срр = а — температуропроводность.
Так как в пламени химические реакции протекают при высоких температурах, в малом интервале температур, то химическая ширина зоны пламени бз составляет небольшую часть ширины тепловой зоны
62 = Ф6ь (8-42)
Где Ф — безразмерный множитель, меньший единицы, численное значение которого зависит от температур Г0 и Гг и от кинетики реакции.
Химическую ширину зоны пламени в свою очередь можно выразить
Как
Б2=ипх, (8-43)
Где т — время химической реакции во фронте пламени.
Преобразуя формулу (8-41) с учетом соотношений (8-42) и (8-43) для скорости нормального распространения пламени, окончательно получаем:
|
И |
![]() „ = УФЛ.. (8-44)
„ = УФЛ.. (8-44)
Из формулы (8-44) видно, что ип зависит от физических свойств смеси и ее реакционной способности.
Из выражения (8-41) следует, что
(8‘46)
Т. е. чем больше иП} тем меньше толщина пламени и время разогрева.



 12 апреля, 2013
12 апреля, 2013  doctype
doctype  Опубликовано в рубрике
Опубликовано в рубрике