Если нужно вычислить распределение в потоке скорости, давления, касательных напряжений, являющихся функциями координат точки и времени, то в жидкости выделяют элементарный объем и заменяют действие окружающей среды на выделенную часть соответствующими силами. Применяя к выделенному объему уравнения механики, полу­чают дифференциальные уравнения гидродинамики, в которые в каче­стве неизвестных величин входят искомые па­раметры: скорость, давление, касательное на­пряжение и др. Однако получающиеся диффе­ренциальные уравнения в частных производ­ных не всегда интегрируются.

В ряде случаев бывает необходимым опре­делить суммарное силовое взаимодействие в конечном объеме жидкости, внутри которого нельзя пренебрегать изменением параметров и не требуется определять распределение этих параметров во всем ее объеме. В этих случаях Рис. 7-2. К выводу закона пользуются способом конечных объемов, сохранения импульса. В жидкости выделяют некоторый конечный

106

Объем и к нему применяют теоремы механики, относящиеся к системе материальных точек. Ниже таким образом рассматривается теорема импульсов.

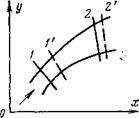
В установившемся потоке, в элементарной струйке, сечениями 1 и 2 выделим произвольный объем жидкости (рис. 7-2). Если рассма­тривать объем 1—2 как состоящий во все время движения из одних и тех же частиц жидкости, то поверхности, ограничивающие выделенную массу жидкости, должны перемещаться вместе с находящимися на них частицами. Так как скорости зависят рт координат, то при перемещении объем будет деформироваться.

Пусть за время йх выделенный объем переместится из положения 1—2 в положение Г—2′. В общей части V—2 объемов, занимаемых выделенной массой жидкости до и после перемещения, количество дви­жения не изменяется, так как скорость во всех ее точках со временем не изменяется. Изменение суммарного количества движения можно подсчитать как разность количества движения двух элементарных масс жидкости, ограниченных сечениями 2—2′ и 1—1′, которые одинаковы и далее обозначены через с1т, а именно

СШтих = (£/^ — V йт, (7-36)

Где и^ и и — проекции на ось х скорости потока в сечениях 2 и 1.

Элементарная масса жидкости

С1т=тсс1х, (7-37)

Где тс — масса секундного расхода жидкости.

Подставляя выражение (7-37) в уравнение (7-36) и учитывая, что согласно теореме импульсов изменение количества движения матери­альной системы равно импульсу приложенных к ней сил, т. е.

С1(ти)=11Рс1х, (7-38)

Получаем:

«с (У*-£/„) = ЕР,. (7-39)

Равенство (7-39) выражает теорему Эйлера об изменении количе­ства движения жидкого объема, т. е. является гидродинамической фор­мой уравнения количества движения.

Уравнение Эйлера показывает, что приращение секундного количе­ства движения на каком-либо участке струи жидкости равно сумме про­екций всех сил, приложенных на этом участке.

В случае прямолинейной струйки постоянного сечения при отсут­ствии трения

2 Р= (р1—р2)Р, поэтому уравнение (7-39) запишется в виде

Ти1=ти2+(р2—р1)Р, (7-40)

Где р2—Р1 — возрастание давления на рассматриваемом участке 1—2.

Из (7-40) следует, что в цилиндрической струйке при отсутствии трения давление может измениться при изменении скорости течения, которое может наступить под влиянием подвода или отвода тепла.

Применительно к затопленной турбулентной струе уравнение (7-39) сохранения количества движения записывается в следующем виде:

Для начального участка:

VI

2риЬ0 = 2р£/», (Ь0 — ух) + 2 Л рПЧу -|- (А — Р») Л н; (7-41)

. Уз

У%

26„р{/!. = 2р Г игйу + (р, — р,), Р, Н. (7-42)

О

В случае свободной затопленной струи, в которой статическое дав­ление можно считать постоянным, уравнения (7-41) и (7-42) упроща­

Ются и записываются в виде:

Для начального участка

1

ИЬо = и2 о фа у г) Ь ^ и*с1ц, (7-43)

О

Для основного участка

1

И2Л = Ь (7-44)

О

Для изобарической спутной свободной струи уравнение сохранения количества движения принимает вид:

Р

ГУ, (II, — и.) <&. = Г и (и — {/,) <1Р. (7-45)

О О