В предыдущих параграфах задача о горении однородной газовой смеси в турбулентном факеле рассматривалась в одной из двух частных постановок. В первой из них газодинамический расчет фронта пламени — поверхности теплового скачка — дополняется предположением о максимальном отклонении потока. Во второй скорость турбулентного горения на фронте считалась заданной априори, Тем самым в неявном виде в основу расчета была положена квазигетерогенная схема. В обоих случаях введение дополнительного условия приводило к отбору единственного решения — для местоположения фронта и для всей задачи в целом.
Рассмотрим в заключение более общий и последовательный расчет факела на основе сочетания методов теории турбулентных струй и теплового режима горения Ш. 30]. Для облегчения задачи введем ряд упрощений, оправдавших себя в теории и расчете диффузионного факела. К числу их относится прежде всего квазигетерогенная модель фронтального горения горючей смеси при конечной скорости реакций. При замене этой схемой реального процесса с протеканием реакций в некотором объеме возникает
необходимость введения нового дополнительного условия для определения местоположения фронта пламени. Это условие легко, однако, выбрать из простых физических соображений. Достаточно сделать вполне правдоподобное предположение о том, что фронт пламени располагается в факеле в месте, отвечающем максимально возможной температуре (и, соответственно, полноте сгорания), как задача получает единственное решение и в принципе доводится до конца. Это значит, что решение позволяет определить координату фронта пламени, а с нею и скорость распространения турбулентного горения, профили характерных величин, полноту сгорания и, наконец, критические условия воспламенения и потухания и их зависимость от основных параметров. И хотя практическое осуществление такого расчета для конкретных условий сопряжено
Со значительными тех* а) б) ническими трудностями,
Принципиальная возможность его представляет несомненный интерес.
Качественную картину горения турбулентного гомогенного факела
Рис. 7-7. Схема гомогенного факела. представим в следующем
Виде. Допустим, что струя стехиометрической горючей смесн вытекает в неограниченное пространство, заполненное воздухом или инертным газом (рис. 7-7, а). Пусть турбулентный фронт пламени занимает некоторое среднее положение. Скорость реакции будем считать при этом конечной, но столь большой, что фронт пламени можно схематически рассматривать как поверхность.
|
|
Допустим, как было сказано выше, что температура максимальна на фронте. Это, конечно, не требует доказательства, так как наличие максимума температуры вне зон горения — в области, в которой источники тепла отсутствуют и происходит одно только перемешивание,— физически нереально. Этим не ограничивается сделанное допущение. Необходимо пойти дальше и допустить, что фронту пламени отвечает максимально возможная в данных условиях температура, т. е. наибольшая скорость сгорания и, соответственно, наибольшее количество сгорающего газа. Действительно, легко представить себе, что фронт горения, не удовлетворяющий этому условию, будет неустойчив. Любое отклонение в этом случае привело бы к повышению скорости сгорания и к «автоматическому» смещению фронта в положение, соответствующее возможному максимуму температуры. Устойчивость этого положения может нарушиться лишь тогда, когда скорость подвода горючей смеси превысит возможную скорость сгорания. Тогда произойдет обычное лотухание ІЛ. 21 ]. Это условие (критическое), как и
всегда в задачах теории теплового режима, также содержится в результатах расчета.
Если же целью расчета является только построение профилей температуры, скорости и концентрации для интенсивного горения вдали от срыва, то достаточно определить местоположение фронта пламени. Его нельзя было бы, однако, найти (без специального допущения) в предположении о бесконечно большой скорости реакции. В этом случае все мыслимые положения фронта равноправны и всем им отвечает одно и то же значение температуры горения. При конечной скорости реакции только одному положению фронта отвечает максимум температуры и полноты сгорания; это положение и является решением задачи.
Количественный расчет проведем на простейшем примере автомодельной задачи о горении стехиометрической смеси в свободном турбулентном плоскопараллельном пограничном слое (см. рис. 7-1).
Имея в виду главным образом качественную сторону, поступим проще — пренебрежем изменением плотности, т. е. будем решать систему уравнений (6-1) для случая р = const. При заметном сокращении выкладок это не внесет существенного искажения в конечные результаты расчета.
Как и при рассмотрении плоского фронта пламени в задаче о диффузионном факеле (см. § 6-1), из уравнений движения и неразрывности находится единое для всего поля течения решение динамической задачи.(профиль скорости). Уравнения энергии и диффузии интегрируются раздельно для областей по обе стороны фронта пламени (поверхности слабого разрыва), а затем полученные решения смыкаются на фронте.
Граничные условия запишем в виде: на внешних границах факела
|
Дг |
|
Д с |
|
= 1, |
|
Д с |
|
Дг |
|
+ « Дс |
|
(7-19) |
|
Дг |
|
= 1. |
|
= 0, |
|
Дг |
|
Д с |
= 1 при у — + оо,
1 при у = — оо;
|
Дс |
— РфОф 1 |
Дс |
|
Ду |
Ду 2 |
|
|
Дс |
Дс |
|
|
Ду |
— Рф^ф 1 |
Ду |
|
На фронте пламени при у.— г/ф Д с = 0, Ді = 0, |
|
Я Р-А |
|
= xk0W (с) ехр |
|
(7-20) |
|
RT ДТ Ду |
|
ДТ |
|
=) |
|
(7-21). |
|
Ду |
Где * —функция, учитывающая отличие среднего значения константы скорости реакции от значения ее при средней температуре в турбулентном потоке; W (с) — функция концентраций реагентов, вид которой определяется порядком реакций; индексы + со и — оо относятся соответственно к горючей смеси и окружающему
Факел газу (продуктам сгорания), индекс «ф» указывает, что значение заданной величины берется на фронте пламени, индексы 1 и 2 относятся к потокам, подходящему к фронту и отходящему от него.
Заметим, что расчет в квазигетерогенном приближении ограничен по физическим предпосылкам (интенсивное горение) областью вблизи максимальной температуры. В этой области различие между средней константой реакций и ее значением, рассчитанным по средней температуре, невелико. Поэтому в дальнейшем примем значение 1 и в расчете в первом приближении пренебрежем эффектом, связанным с влиянием турбулентных пульсаций температуры. Роль его, как указано в § 5-3, особенно велика при низких значениях температуры — вблизи области воспламенения (и, конечно, при высоких значениях интенсивности турбулентных пульсаций).
Для простоты решения примем Т+<п = ~ Тоо, ср = const, т. е. At = срАТ, а также W (с) = рс. Последнее отвечает простой реакции первого (суммарного) порядка. Решение автомодельной задачи известно [см. формулы (6-12) — (6-17)].
Для определения неизвестных из газодинамического расчета значений температуры и концентрации на фронте пламени используем условия (7-20) и (7-21) — уравнения материального и теплового баланса, которые легко привести к виду (6-21) и (6-22), обычному в теории теплового режима горения [Л. 21 ].
Стационарные значения температуры и концентрации определяются из условия равенства теплоотвода и тепловыделения в зоне горения:
Фі = Ф.. (7-22)
В это уравнение входит неизвестная еще величина срф — координата фронта пламени. Задавая значения ср^ из соотношения (7-22), можно определить величину стационарной температуры горения для заданных условий (м+оо, с+оо, Т+к и т. д.).
Зависимость температуры на фронте от координаты срф схематически показана на рис. 7-7, б. Согласно развитым в начале параграфа представлениям, примем для обеспечения единственности решения условие
= 0. (7-23)
%
Применяя условие (7-23) к соотношению (7-20), получаем связь между Максимальной температурой горения и координатой срф:
9 = lnf ‘ І * (?"24) t Х [erf (if У*г)]ф J
Используя выражения (7-22) и (7-24), приходим к трансцендентному уравнению, определяющему местоположение фронта пламени, в виде зависимости координаты фронта фф от теплотворности смеси:
________________ !________________________________ !________ х
J______________ і___________ » і + erf (<Рф ут}
X———————————— ——————————— . (7-25)
In————————— =———— ]-в„
, Ji [‘+erf (уф УЧ)]
[ т Ы(^т)|ф
Следует отметить, что уравнение (7-25) имеет три корня. Два из них, как известно из теории теплового режима, определяют устойчивые режимы: горение и медленное окисление. Третий корень, соответствующий промежуточному режиму, отвечает неустойчивому состоянию системы (рис. 7-8). В связи с этим при решении уравнения (7-20) необходимо выбирать корень, отвечающий верхнему режиму — горению.
|
Рис. 7-8. Зависимости ifo (Є) и г|>2 (6) при различных значениях параметра ft (стрелкой указано направление возрастания ft). |
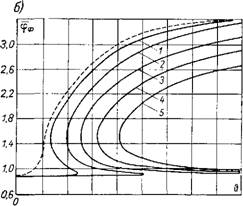
Результаты расчета местоположения фронта пламени в зависимости от теплотворности смеси, скорости потока и других параметров приведены на рис. 7-9. Как видно из графика, повышение теплотворности смеси вызывает смещение фронта пламени к внутренней границе пограничного слоя. Этот результат подтверждает высказанное Г. Н. Абрамовичем [Л. 1 ] предположение о расположении фронта пламени при горении высококалорийных смесей вблизи границы области смешения. Увеличение приведенного коэффициента турбулентной структуры струи и повышение реакционной способности смеси k0 приводят также к смещению фронта пламени в сторону набегающего потока. Противоположное по характеру влияние оказывает на местоположение фронта пламени увеличение скорости струи.
|
145 |
Для примера на рис. 7-9, б пунктиром нанесена также зависимость хрф = f (8) при другом значении начальной температуры смеси: = 0,064. Как видно из рисунка, в случае увеличения начальной температуры смеси процесс горения может проходить и в бескризисном режиме. Последнее находится в полном соответст-
6 Заказ М 2565
вии с известными положениями теории теплового режима [Л. 211. Зависимость температуры горения от теплотворности смеси приведена на рис. 7-9, б.
Значительный интерес представляет вопрос о влиянии параметров процесса на полноту сгорания. На рис. 7-10 показана зависимость полноты сгорания от а* начальной скорости исте
Чения газа и теплотворности смеси. Из этого графика видно, что увеличёние скорости или уменьшение теплотворности приводит к снижению полноты сгорания.
Приведенные выше качественные выводы проиллюстрируем следующим примером.
Рассмотрим горение смеси углеводородного топлива с воздухом, характеризующееся стехиометри — ческим соотношением 2 = = 15-5 (по воздуху), теплотворностью 104 ккал/кг и энергией активации Е = = 4-Ю4 ккал/моль-град. Значение приведенного кинетического комплекса k0 положим равным 12-10е. Для данных условий величина безразмерной характеристики теплотворности составляет 0,092. Этому значению теплотворности газовой смеси (при —— = 20 м/сек) соответствуют значения фф = 2,26 и 0ф = = 0,148. Принимая коэффициент турбулентной структуры струи при горении равным 0,05, получаем величину угла наклона фронта к оси arctg (у/х) = 5°30′.
|
0.16 |
|
0.12 |
|
0.08 |
|
0,02 0,04 0,06 0,08 0.1 0,12 |
|
От |
|
0,02 0,04 0,06 0,08 0,1 0,12 0,14 0.16 |
|
Рис. 7-9. Зависимость температуры горения Оф (а) и координаты фронта пламени фф (б) от теплотворности смеси 1 — при «„ = 1 м/сек’, 2 — при = 2,71 м/сек; в — при U „о = 7,3 м/сек-, 4 — при = 21 м/сек-, 5 — при = 54,2 м/сек. |
|
А) |
|
0,5 |
|
12.5 |
|
25 |
|
37,5 м/сек |
|
|
На рис. 7-11 приведена фотография турбулентного гомогенного факела, полученная на бунзеновской горелке с диаметром сопла 30 мм. Сплошной линией показано рассчитанное по соотношению (7-25) местоположение фронта пламени. Из рисунка видно, что имеется качественное соответствие расчета с опытом Следует отметить. что результаты расчета цают возможность определить ос — редненное значение скорости турбулентного распространения пламени. Действительно, зная фф, можно по правилу В А. Михель — сона нзйти значение ит из соотношения (7-18). Определенная таким образом скорость tj рбулентного горения учитывает факторы как газодинамической, так и кинетической природы. Косвенно (через
Посредство эмпирической постоянной а) на ней сказывается также уровень турбулентности потока и др
На рис. 7-12 представлены расчетные данные по влиянию скорости набегающего потока на местоположение фрпнта пламени и на величину скорости тур булентного распространения пламени. Как видно из графика, увеличение скорости истечения смеси приводит к уменьшению угла наклона Фронта по отношению к направлению движения потока и росту скорости турбулентного распространения пламени ГТри этом зависимость ит ■- f(uj может быть аппроксимирована (как это обычно делается в теории горения) в виде
Ыт = kul К. — "’)- (7-26)
Как следует из сопоставления выражения (7-26) и соотношения (7-18), показатель степени п да 0,75.
Приведенные графики иллюстрируют глаьным образом расчет местоположения фронта, а также влияние скорости потока и
теплотворности на скорость турбулентного распространения пламени. Все необходимые данные для построения профилей скорости, температуры и концентрации имеются в приведенных выше расчетных формулах. Вид основных профилей для гомогенного факела внешне мало отличается от вида профилей для диффузионного факела, если расчет выполняется в упрощающем предположении р = const. Последнее, конечно, совсем необязательно. Заметим в связи с этим, что расчет по методу подобия ри2 (как в § 7-3) приводит к заметному увеличению на фронте пламени продольного компонента скорости по сравнению с его значением в потоке свежей смеси (их2 > их1). Отсутствие надежных опытных данных не позволяет проверить справедливость этого результата, согласующегося с оценкой, полученной из газодинамического расчета, и указать оптимальный путь детального расчета. Несмотря на это, развитая в этом параграфе расчетная схема гомогенного турбулентного факела при конечной скорости реакции в принципе является законченной и качественно отвечает эксперименту.



 13 августа, 2012
13 августа, 2012  admin
admin 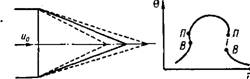


 Опубликовано в рубрике
Опубликовано в рубрике