Для теоретического исследования продольных акустических колебаний в опытных установках, двигателях или топках иадо задаться некоторой идеализированной схемой. При теоретическом анализе рассматриваемого явления будем считать, что все перечисленные выше устройства допускают сведение их к длинной цилиндрической трубе, которую можно разбить на ряд участков, разделениях короткими зонами, внутри которых происходит процесс теплоподвода. Движущийся по этим участкам газ (воздух или продукты сгорания) в отсутствии колебаний пе претерпевает никаких изменений. Обычно достаточно рассмотреть два таких участка — один, соответствующий подводящему трубопроводу, а другой —камере сгорания. IJa первом из названных участков не будет учитываться возможпое изменение проходных сечений, наличие гидравлических нотерь, изменение состава газа вследствие введения в поток горючего и т. п. На втором участке не учитывается догорание и смешение газов в части камеры сгораяпя, прилегающей к выходному соплу, а также гидравлические потери, потерн тепла, связанные с теплоотводом через стенки камеры сгорания, и т. п.
Процесс горения в пршгятом здесь представлении осуществляется в одной или нескольких областях малой про-
К р о к к о Л у л Д ж п и Ч ж о п С и її ь-и, Теория пеустопчи BOCTU горения в жидтсостиых peaкти вных двигателях, 11 Л, Москва, 1058.
Тяженностп. Эту малость областей горения следует понимать как малость по сравнению с длпнамп волн продольных колебаний, а следовательно, п по сравнению с общей длилой трубы (установки). С целью упрощения постановки задачи будем пренебрегать протяженностью зон горения, замеппв эти области поверхностями сильных разрывов.
Таким образом, теоретическая расчетная схема соответствует одномерпому газовому течению в цилиндрической трубе, разделенному в общем случае одной или несколькими поверхностями сильных разрывов. Свойства поверхности разрыва 2 существенно зависят от процесса горения в той области, которую эта поверхность представляет. Эти существенные свойства можно сформулировать лишь отказавшись ет упрощенного одномерного рассмотрения процессов, идущих п зоне горенпя.
Поэтому при рассмотрении процесса распространения возмущений между поверхностями разрывов будет использоваться одномерная схема, а нрп формулировании свойств поверхности разрыва — трехмерпая схема явлепия. Характеризуя свойства зоны тспдододвода, будем, как правило, пренебрегать гидравлическими сопротивлениями и изменением агрегатпого состояпня топлива нригорепин. (Примеры процессов, когда этого делать нельзя, проведены в последней, десятоіі главе.) Поверхности разрыва могут вводиться не только для описання процесса горения, но и в других случаях, когда параметры течения претерпевают сильное изменение па коротком участке.
Помимо свойств поверхности 2, разделяющей течение на два участка, следует определить свойства течепия на концах трубы. В зависимости от рода подлежащей исследованию задачи краевые условия приобретают тот или иной вид. В одном случае это будут обычные акустические условия, в другом —условия, характеризующие идеализированные свойства сопла Лаваля или аналогичных устройств.
Так как основным содержанием последующих глав является исследование колебательных процессов, имеющих акустическую природу, ниже будет применяться метод малых возмущений. Осповпой задачей исследования является, как правило, изучение устойчивости газового течения в трубе оппсаиного тина по отношению к малым возмущениям. Если процесс в идеализированной схеме окажется колебательно-неустойчивым, то будет сделано естественное предложение, что подобная неустойчивость приводит к автоколебаниям.
Как известно, для полного решения задачи об автоколебаниях требуется учет существенно иелинеиных зависимостей. Задача такого рода рассматривается в главе VIII. Главным упрощающим предположением служит допущение, что все существенно нелииейиые зависимости содержатся в свойствах поверхности разрыва 2. Что касается процессов распространения возмущений между поверхностью разрыва и концами трубы, то будот предполагаться, что эти процессы достаточно хорошо описываются линейными уравнениями и па режиме установившихся автоколебаний.
Рассматриваемые ниже автоколебания акустического тииа можно охарактеризовать как вызванные наличием обратной связи. В случае возбуждения автоколебаний процессом горения (вибрационное горение) обратная связь будет приводить к шняишо акустических колебании па процесс горения. Поэтому в специальной главе будет рассмотрен целый ряд физических явлегши, приводящих к замыкапшо подобной обратной связи. Однако в больппш — стве теоретических расчетов обратная связь не конкретизируется, а вводится чисто формально, как зависимость существенного параметра в зоие горения (яа поверхности разрыва 2) от величины колебательной составляющей скорости пли давления.
Прежде чем переходить к систематическому изложению предмета, иолезио сделать ряд предварительных замечаний, имеющих отношение к методу изложения, принятому в sosл&дукщих главах.
Ниже будут различаться режимы колебаний, характеризуемые возрастанием амплитуды некоторой величины Ь со временем /, постоянством амплитуды и, наконец, убыванием ее. Ути три случая изображены на рис. 3 (а, б и в). Первы/t случай является примером неустойчивого, последний — устойчивого, а средний — нейтрального процесса.
При изменении какого-либо существенного параметра колебательная система может из устойчивой превратиться в неустойчивую и наоборот. Всюду будет делаться предположение. что ири таких переходах (ecbra они совершаются непрерывно), колебателыгая система обязательно нройдет через режим нейтральных колебаний. Этох_4>еяшм часто называется границей устойчішости. —
""Обычно задачей теоретического анализа является нахождение границы устойчивости. Зпая эту границу, условие
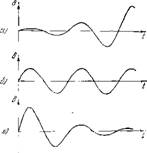
1’ис. 3. НеустоіЬпзвио, лгштральпые и затухающие колебания.
Устойчивости системы можно сформулііровать в виде некоторого неравенства, что весьма удобно для практики. Исследование режима нейтральных колобагпгй оказывается обычно ироще исследования режимов с измешшщимнси амплитудами. Это связано с тем, что при нейтральных колебаниях изменения переменных синусоидальны.
Здесь следует указать, что не всякий режим с постоянными амплитудами колебаний является нейтральным и соответствует границе устойчивости. Тем же свойством обладает и режим установившихся автоколебаний, хотя оп соответствует области неустойчивости. Одиако в отличие от нейтральных колебаний автоколебания описываются нелинейными системами уравнений н сам факт анализа нелинейной системы в дальнейшем пзложептш будет особо оговариваться.
Известпая трудность возпикает при сравнении опытпых данных с теоретическими расчетами. Дело в том, что если в опыте установилась некоторая частота и амплитуда колебаний, то это практически всегда означает, что в системе возникли автоколебания, т. е. явленпе, описываемое пели — нейными соотношениями. В то же время замеренные в этих опытах частоты п даже относительные амплитуды колебаний будут нередко сравниваться с теоретическими соотношениями, справедливыми лтшіь для линейных процессов. Такое упрощение возможно потому, что рассматриваемый ниже тин автоколебаний близок по своему характеру к малым колебаниям, описываемым ли — иейиыми системами уравнений.
Достаточпо иолное представление о нроцессе колебаний можно иолучить, имея кривые пзменеиия всех иеремеиных в фуик — ции времени. На рпс. 4 показан соответствующий пример. Здесь бі», bp, 6Q — возмущения скорости, даплепия и теилоиодвода соответственно. Имея ири — вадепный график, можно судить о периоде колеба — яий Т, амплитудах колебании 6с0, бр0 и 6<2о и о фазовых сдвигах между приведенными переменными. Так, если сравнивать фазы другпх колебаний с фазами колебания давления 6р, то фаза 6г> будет отличаться от фазы Ьр па <р,, а фаза 6Q на ср.2.
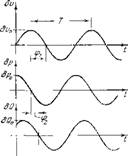
Ряс. 4. Уаяпснмости колебательных составляющих параметров течения от времени.
У
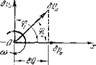
Рис. 4.
В тех случаях, когда частота колебании (или однозначно связанный с нею период колебаний) особого интереса не представляет, а существенными являются относительные а мнлитуды колебаний отдельных переменных и их взаимные фазовые сдвиги (иначе говоря, нужны только амплитудно — фазовые соотношения), можно применить более наглядный способ графического изображения режима колебании. Он представлен на рис. 5, где изображен тот же процесс, что и на рис. 4. Как видно пз рис. 5, указашшй способ сводится к построению векторной диаграммы. Каждая переменная изображается в виде вектора, длина которого равпа амшштуде колебаний, а углы между векторами равны фазовым сдвигам между переменными. Если мысленно скрепить эти векторы между собою и придать им общее вращение вокруг центра О с частотой со, то, наблюдая
За проекциями векторов на некоторое направление, например на ось х, можно получить синусоидальное изменение переменных во времени, с заданными амплитудами и фазовыми сдвигами. Положение векторов па рис. 5 соответствует моменту времени? = 0 на рис. 4; путем вращения совокупности изображенных векторов но часовой стрелке можно нолучпгь зна-
Рис. 5. Векторная диаграмма чегаш 6v> ЬР 11 6Q ви все нроцесса, изображенного на следующие моменты времени.
В тесной связи с последним способом изображения
Процесса колебаний стоит вопрос о способе аналитической занисн соответствующих выражений. Переменную величину, имеющую амплитуду и фазу, можно изобразить в виде вектора. Аналитически вектор можно записывать, пользуясь методами векторного анализа нлп плоскостью комплексного церемонного. В дальнейшем изложении будут использованы оба эти способа записи неремепных. При этом надо всегда иметь в виду, что если сумма или разность двух комплексных чисел вполне может быть заменена суммой или разностью соответствующих векторов, то этого, как известно, нельзя сказать об их произведении. Следовательно, особую осторожность надо проявлять тогда, когда приходится рассматривать произведение переменных или пронзведонне переменного на некоторый коэффициент, осли последний изменяет не только величину, но п фазу.



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике