В двух предыдущих параграфах были рассмотрены некоторые общие свойства волн возмущений и теперь можно вернуться к рассмотрению задачи о распростране­нии возмущений, начатому в § 5 для простейшего случая.

Рпс. 12. Эшори мгновенных значении и, се и. v.

Оказывается, что решения задачи с учетом начальных н Краевых YCYhHULH в той форме, как это делалось в § 5, обычно можно избежать. В огромном большинстве практи­чески интересных случаев возбуждения акустических
колебаний теплоиодводом решение задачи с учетом на­чальных условий интереса не представляет.

Это связано главным образом с тем, что обычно коле­бания возникают в результате развития каких-то весьма малых — и неопределенных пачальпых возмущений, кото­рые всегда присутствуют в впде неизбежной флуктуации параметров течения. Вне зависимости от характера этих начальных флуктуацнй акустические колебания в потоке в процессе своего развития (при условиях, благоприят­ствующих такому развитию) достигают заметных ампли­туд, рост которых в конце концов останавливается. В ре­зультате колебательная система выходит на режим уста­новившихся акустических колебаний, характер которых, как правило, пе зависит от конкретного вида начальных возмущений. Пример такого процесса будет приведен в главе VI.

Указанное обстоятельство упрощает исследование во­проса, поскольку позволяет отказаться от формулиро­вания начальных условий — задачи почти невыполни­мой вследствие крайней неопределенности малых началь­ных возмущепнй течения.

В теории колебаний описанный ход явления известен как случай мягкого самовозбуждения автоколебаний.

Для того чтобы система возбуждалась указанным об­разом, она должна быть неустойчивой по отношению к ма­лым возмущениям течения. Процесс самовозбуждения можно представить себе следующим образом. В началь­ный момент времени существует некоторое малое возму­щение течения, удовлетворяющее краевым условиям. Это возмущение можно представить как наложение гармо — пик системы1), причем численное зпаченне амплитуды каждой гармонпкп [например, чисел Аик в суммах (5.5)) определяется впдом начального возмущения. Поскольку начальные возмущения могут иметь самый различный вид, следует предположить, что амплитуды всех гармоник отличны от пуля. Если среди гармоппк системы хотя бы одна неустойчива, то ее амплитуда будет возрастать со

‘) Здесь и ішже не будет делаться разипцы между попятиямн гармоштка п стоячая волна, соответствующая ей, в тех случаях, когда пе может возникнуть путаницы.

Временем, возмущение течения перестанет быть малым и неустойчивая гармоника, обогнав в своем развитии есє остальные, придаст всему процессу колебаний свойствен­ные ей черты, вне зависимости от вида начального воз­мущения.

Таким образом, оказывается, что начальные условия сформулировать не только трудно, но и нецелесообразно. Одиако, если не учитывать начальные условия, в матема­тическом решении задачи должна появиться некоторая неон р еде л еппо сть. Эта неопределенность скажется в том, что начальные амплитуды стоячих волн (числа Avk и останутся неизвестными. Легко сообразить, что в огром­ном большинстве случаев это не может помешать отыс­канию результата, представляющего действительный ин­терес, поскольку выше было указано, что основным является вопрос о том, нет ли среди гармоник системы неустойчивых, амплитуды которых со временем стре­мятся к пеограинчеиному возрастанию (этому возраста­нию ставят предел нелинейные свойства системы, никак пе зависящие от начальных условий). При этом вопрос о начальной величине амплитуды, которая стремится беспредельно возрастать, является совершенно второ­степенным.

Основываясь на сказаппом, можно следующим образом сформулировать задачу, подлежащую исследованию.

Нужно найти решение системы уравпеннй возмущен­ного движения, удовлетворяющее заданным краевым усло­виям, п дать количественную оценку устойчивости (или неустойчивости) каждой гармопнки решеиня, предполагая, что в момент времени т=0 все гармоники имеют некоторые отличные от нуля начальные значения амплитуд возму­щения.

Решения задач о колебаниях в потоке газа, движуще­гося по трубе с двумя открытыми концами или по трубе с одним закрытым концом, приведенные выше, дали для всех гармоник синусоидальные колебания, амплитуды которых не возрастают и пе убывают с течением времени. При желапни получить более общий результат следует воспользоваться краевыми условиями более общего вида, не ограничиваясь случаями узлов давлеппя или скорости.

Для того чтобы не усложнять выкладки, рассмотрим сравнительно простую задачу о возбуждении колебаний в том случае, когда на выходе из трубы имеется узел дав­ления, а на входе выполняется однородное условие р = Ви.

Таким образом,

P = Bv при £ = (), | — (8.1) р = 0 пря 1 = 1. J

Поскольку условия (8.1) не содержат возмущения энтро­пии 5, задача может быть решена для двух первых урав­нений системы (4.10) независимо от третьего. Решение задачи проведем по той же схеме, что и в предыдущих параграфах. При I = 0 фг/(і) = 1, ф2(£) =0. Тогда формулы (4.13) вместе с первым из краевых условий (8-1) дадут

При |=1 условие р = 0 вместе со вторым равенством (4.13) и с учетом только что полученной связи между Ар и А0 даст соотношение

Ч>г(1) + В<р1(1) = 0,

Если отбросить тривиальный случай Ар — AV = Q.

Обратившись к формулам (4.14), сразу получаем урав­нение для нахождения р:

«рт<8-2>

Пусть число В будет вещественным. Это допущение не искажает общей картины изучаемого явлеппя, но сильно упрощает выкладки.

После подстановки p-v-j-ішв уравнение (8.2) нетрудно прийти к следующей системе, связывающей только вещест­венные переменпые:

2v 2(0 1 +в К

2v. 2ш — (8-3)

Второе уравнение сразу определяет ряд частот, пз которого ножно выбрать частоты, удовлетворяющие и первому уравнению. Этот ряд дается равенством

(1-М*)if- (/< = 0, 1,2,3, …).

Нетрудно видеть, что по все эти частоты удовлетво­ряют системе. Действительно, показательная функция ехр —2v а может принимать лишь положительные значе-

Ппя п, следовательно, знак cos н знак дроби ^ должны быть одппнковыми. Знак же cos зависит от того, четные нлн нечетные значения к берутся.

Таким образом, окончательное выражение для частот системы га можно записать в следующем виде:

, f /с = 0,2,4, …. если f±!>0, " = -Вв (8.4)

| 7с= 1, 3, 5, . . ., если ffrfcO.

Поскольку знаки дроби | п велпчппы cos всегда совпадают, a cos ^ 110 абсолютной велпчіиіе

Равен едппице, пз первого уравнения системы (8.3) можно найти v

1 — м* , 114-в і.„ ..

V = 2 ІП ‘ <8’5>

Прежде чем подвергнуть анализу полученный резуль­тат, следует сказать о физическом смысле величины v. С зтон целыо удобно вернуться к решению (4.13). Если рассмотреть процесс колебаний в некотором произвольном сечении трубы 1 = 5], то стоящие в прямых скобках выражения примут постоянные значения, нір можпо будет записать в виде

Где At и А2 — некоторые постоянные (для избранного сечеппя) величипы.

Поскольку обе величины изменяются в зависимости от временя одинаково, рассмотрим более подробпо поведе — J В. в. Раугаеабак
пне одной из них, например v. Подставив (3 = v-[ ш), получим:

V = A^evx (cos cot + і sin сот).

Стоящее в скобках выраженио показывает, что вели­чина v колеблется около значения г>=0. Показательная функция времени, стоящая множителем при величине А1} характеризует изменение амплитуды колебаний со вре­менем.

Если v>0, то показательная функция будет неогра­ниченно возрастать со временем и это будет указывать на неустойчивость процесса — амплитуды возмущений v, р п других параметров течения будут иметь тенденцию к беспредельному росту; величину v в этом случае часто называют инкрементом возрастания колебания.

Если v<0, то показательная функция будет убывать со временем, приближаясь к нулю. Следовательно, имеет место устойчивость течения, всегда можно указать отрезок времени т15 в течение которого амплитуды возмущений станут по абсолютному значению меньше любой наперед заданной как угодно малой положительной величины. В этом случае число v называют декрементом затухания колебаний.

Случай v=0 является промежуточным. При v=0 ампли­туды колебаний не возрастают и не убывают со временем. Это состояние — режим установившихся или нейтраль­ных колебаний — представляет особый нптерес потому, что его можпо рассматривать как режим, соответствую­щий границе устойчивости. Действительно, если устой­чивость системы изменяется непрерывно при непрерывном изменении какого-либо параметра системы, то переход от устойчивости к незгстончдвостн пли наоборот связан с переходом через режим v=0.

Таким образом, в дальнейшем можно будет восполь­зоваться следующими признаками устойчивости:

V >• 0 — течение неустойчиво, v <С 0 — течение устойчиво, v = 0 —установившиеся колебания, -.^V граница устойчивости.

После :>того краткого отступления вернемся к рас­смотрению полученного выражения для v.

Из (8,5) следует, что прп В — 0 процесс нейтрален, так как ему соответствует v=0. Этот результат совпадает с по­лученным ранее выводом, поскольку равенство £=0 означает, как это следует из краевых условии (8.1), что ие только на выходе, по и на входе находится узел давле­ния j=0. Такой же результат (v = 0) дает и подстановка

V>0

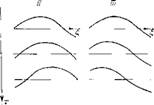
Рис, 13. Эюоры волл | it | и I к; І для неустойчивого (v>0) в устойчивого (v<0) течения.

Z? = со (иодобиое условие означает существование узла скорости на входе в трубу).

В отличие от пазванных случаев при всех других В величина v принимает значения, отличные от пуля. При В > О v > 0 її течение неустойчиво. При В < 0 течение будет устойчивым (v < 0).

Таким образом, введение несколько более сложного краевого условия, чем использованные в предыдущих параграфах узлы скорости пли давления, сразу приводит к качественно новой картине. В зависимости от числа В течеппе может стать как устойчивым, так и неустойчивым.

При ф О эпюры амплитуд возмущений получаются ОТЛИЧНЫМИ от тех, которые приведены в двух предыдущих параграфах. Чтобы не перегружать текста, приведем лить эпюры И и wj, воспользовавшись формулами (*.12). Для каждого заданного г получатся кривые, представленные на рис. 13. Стрелкноколо кривых указы­вают направление движения волн и и w.

Для неустойчивого течения (v > 0) амплитуды [ и | п I w I в направлении стрелок уменьшаются; это можно истол­ковать в том смысле, что вышедшие позже акустические импульсы имеют бблыпую амплитуду, т. е. система уве­личивает амплитуды со временем. Для устойчивого тече­ния (v < 0) наблюдается обратная картина. Следует также заметить, что эпюры на рпс. 13 построены для некоторого фиксированного момента времени. Для каждого последую­щего момента времени эпюры для v > 0 будут соответст­венно увеличивать свои ординаты, для v < 0 — умень­шать.

Обычно в акустике рассматриваются системы, которые характеризуются лнбо колебаниями с достоянной ампли­тудой (v— 0), либо убывающими со временем амплитудами (v < 0). Первый случай соответствует идеализированной схеме явления, в которой ire учитываются неизбежные потерн, а второй —реальным процессам, связанным с дис­сипацией энергии. В рассмотренном примере при В > 0 получено v > 0, что является, быть может, неожиданным для привычных акустических явлений. Здесь происходит не рассеивание акустической энергии в среде, которое неизбежно во всякой реальной системе, а как бы зарож­дение все новых и новых количеств акустической энергии, затрачиваемых на все более интенсивную раскачку среды. Вопрос об источнике этой эпергпн будет подробно рас­смотрен в следующей главе. Здесь хотелось бы только подчеркнуть выявившуюся принцип пальную возможность самовозбуждения акустических систем рассматриваемого типа. При этом полезно обратить внимание на то, что причина самовозбуждения системы локализована в рас­смотренном примере во входпом сечении Труб. Конечно, реальный физический процесс, который был формально

Выражен в виде краевого условия p — Bv, происходит в некотором объеме в области, прилегающей ко входному сечению, но важно то, что если путем надлежащей идеали­зации этот процесс удастся свести к некоторому соотпо- щенпго, справедливому для одного сечения потока (здесь входного), то открывается путь к сравнительно простому математическому описанню явления в целом. Это обстоя­тельство будет широко использовано в настоящей кипге.

Пользуясь иеремепными и и w, можио более наглядно истолковать результат, полученньтіі в настоящем пара­графе. Если записать краевые условии (8.1), воспользо­вавшись формулами (4.9), при помощи переменных и и w, то они примут следующий вид:

Таким образом, импульс двинувшись от левого конца (5 = 0) к правому концу (|=1), отразится от последнего, ие изменив величины. II в виде импульса Wl = Ui пойдет влево. У левого конца трубы пришедший импульс Wi отразится в виде импульса иц, причем ііцфті._В зави­симости ОТ величины В отраженный импульс 11ц будет по абсолютной величине больше пли меньше пришедшего. Если #>0, то 1 «и | > | W[ |, а так как этот процесс отра­жений импульсов от обоих концов трубы будет продол­жаться, то амплитуды возмущений будут иметь тенденцию к неограниченному возрастанию. Прп каждом отражении от левого конца пришедшие импульсы будут испытывать как бы дополпительпип внешний толчок. В случае #<0 процесс отражения у левого конца трубы имеет обратный характер ■— импульсы у мен [.та ют свою интенсивность.

Этот вывод повторяет результаты, полученные в виде формулы (8.5), Кроме того, проведенное рассуждение подтверждает локализацию причины возбуждения си­стемы или гашения колебаний во входном сечении прп 1=0.

Чтобы проиллюстрировать приведенные выше рас — суждеппя, рассмотрим реальный случай течения, в ко­тором краевое условие па входе приобретает вид (8,1) или (8.7).

На испытательных стендах для исследования процес­сов горения или другпх целей нередко применяется сле­дующая схема течения (рпс. 14). По трубе АВ от соответ­ствующей воздуходувки но дается воздух под нужным давлением. Участок трубы ВС предназначен для проведения различных опытов, например, связанны*

С организацией процесса гореппя в концевой части тру­бы ВС. Чтобы процесс горенпя, который может сопро­вождаться хлопкамп прп включении системы зажигания, быть неустойчивым п т. д., не влнял на работу воздухо­дувки, в сечении ВВ делается сужение, причем настолько сильное, чтобы справа от ВВ образовалась небольшая область со сверхзвуковыми скоростями течения. Тогда, как известно из гидромеханики, никакие возмущения (если только они не разрушают области сверхзвукового течения) не могут передаться из участка трубы ВС вверх по течению в участок АВ. Этим достигается то, что воз­духодувка работает в заданном установившемся режиме вне зависимости от того, какие нестационарные про­цессы имеют место на участке ВС.

Таким образом, образо­вание сверхзвуковой зоны течения в окрестности се­чения ВВ способствует спокойной работе возду­ходувки. Поставим теперь вопрос о том, как скажется наличие подобного сужения па процессах, идущих в правой части онытяон установки, в частности, как это скажется на характере акустиче­ских колебаний в ней. На конце С краевое условие можно написать сразу: р=0, так как открытый конец трубы со­общается с впешптш пространством. Это приближенное краевое условие справедливо в тех случаях, когда в се­чении С пе возникает звуковой скорости течения (кри­зиса), связанного с большим теплоподводом па участ­ке ВС. Что касается краевого условия на входе в тру­бу ВС, то оно не является очевидным.

Рнс. 14. Трубопровод с критиче­ским сужением.

После сужения В В возникает, как уже говорилось, сверхзвуковое течение. Это сверхзвуковое течение тормо­зится затем в некоторой достаточно сложной системе скачков уплотнения, характер которой предсказать пра­ктически невозможно. Поэтому попытка записать крае­вое условие путей! анализа газодинамической картнпы течения не может быть прпзпапа целесообразной. Здесь деожно .воспользоваться ^ем, что перед сечением ВВ поток
всегда невозмудеп и поэтому параметры его течения посто­янны и пе зависят от акустических колебаний, происхо­дящих справа от ВВ. В частности, секундный расход воздуха, пересекающего сечение ВВ, постоянен. Если объем области, в которой тормозится сверхзвуковое те­чение мал, и мгновенное количество массы воздуха, заключенного в пем, не меняется, то можно считать, что и в лежащем несколько правее ВВ сечении, где скорость потока вновь дозвуковая, секундный расход воздуха иостоянеп, несмотря на наличие колебаний давлення и скорости. Следовательно, на входе в трубу ВС будет выполняться условие

OV = const.

Вудем считать процесс на входе в трубу ВС изоэнтро — ничным. Тогда после линеаризации этого соотношения и перехода к принятой системе безразмерных перемешшх нетрудно получить краевое условие на входе:

(8.8)

Р +

И = 0.

М

Сравнивая его с первым краевым условием (8.1), сразу 1

Получаем В= —

Таким образом, в рассматриваемом случае имеет место неравенство В<0 и, следовательно, течение всегда устой­чиво. Этим рассмотренный тип течеппя существенно отличается от течения в трубе, открытой с двух концов или закрытой с одного конца, где колебаппя получались нейтральными (v=0). При создании стендовых установок по счече. приведенной на рис. 14, в области ВВ будет н[ю||слс|д!!ть демпфирование колебаний, и это будет спо­собствовать более устойчивому протеканию процесса, идущего в трубе ВС (напрпмер, горения).

Таким образом, точению в трубе, характеризуемому постоянством расхода газа на входе, присуще демпфиро­вание акустических колебаний. С точки зрения получе­ния спокойного горепня, менее склонного к внбрацпям, это свойство является полезным. Поэтому создание стен­дов по схеме рпс. 14 для целей изучения закономерностей стационарпого процесса горения будет правильным.

Однако в тех случаях, когда целью опытов является изу­чение процессов возбуждения колебаний, создание уста­новок с постоянным расходом газа па входе может ока­заться нецелесообразный!.

Если поставить вопрос о физических процессах, проис­ходящих на входе в трубу и ведущих к рассенванню энергии, то в каждом конкретном случае механизм рас­сеивания эпергпи может быть своим.