Рассмотрим процесс, характеризуемый условием bv} = = 6i> = 6i>2. Тогда dbv = 0 н согласно формуле (11.17) два первых члепа в равенстве (11.19) дадут нуль. Это означает, что вся энергия акустических колебании заимствуется пз кинетической энергии течепия. Наоборот, при процессе, характеризуемом условием Ьрх = bp = bp2, вся энергия акустических колебаний будет заимствоваться из тепловых члепов — внешнего тенлоподвода п внутренней энергии, перепоспмой течением. В каждом пз этих двух случаев колебательная система будет использовать какой — либо один источник энергии, п с этой точки зрения процессы в зоне теплоподвода, характеризуемые условиями Ьі^ = б:»= 6а, п Ьр1 = др — др2, можно назвать элементарными. Нетрудпо, однако, показать, что к элементарптлм процессам следует отнести более широкий класс процессов в зоне теплоподвода.
С точкп зренпя запмствопаштя энергии пз располагаемых источников приведенные _выше процессы и..зоне теплоподвода, характеризуемые условиями 6^ = 6v = 6f2 и б/?, = bp = б/?2, эквивалентны более общим процессам, характеризуемым равенствами = и Ьр1 = Ьрг. Действительно, сравним, например, процессы с 6t’r = 6с’2 и с floj = bv = 6у2.
Если предположить, что на границах области о все величины в обоих случаях изменяются одппаковым обра — т т
Зом н значения ~ АР dt и — ^ совпадают, то
О 6
Правые части равенств (Л. 17) и (11.18) будут численно совпадать. Одинаковыми будут, следовательно, и стоящие слева иптегралы. Таким образом, процесс заимствования энергии для иоддержаиия колебаний из располагаемых источников энергии не связан с характером изменения bp и bv вдоль области а, а однозначно определяется значепиями переменных на границах области а при условии, что задана величина изменения среднего значе — т
Пня теплоподвода — ^ AQ dt=AQcv (предполагается Р = 0). 6
Из (11.11) очевидно, что условия Ьр1 = Ьрй и 6t>x = 6a> совпадают с условиями 6Х = 0 и ЬЕ=-0.
Будем изучать, основываясь на сказаппом, следующие элементарные процессы.
Первый элементарный процесс характеризуется условием 6/^ = 6^2, или 6.Х = 0. Заимствование энергии происходит из внешнего теплоподвода и потока внутренней энергии.
Второй элементарный процесс характеризуется условием 6а1 = 6и3, или 6Zs = 0. Заимствование энергии происходит нз потока кинетической энергии.
Рассмотрим более подробно первый элементарный процесс, в котором вся энергия для поддержания автоколебаний заимствуется из тепловых члепов (теплоподвод и впутреппяя энергия). Условие Ьрі = Ьрг при сохранении неизменной величины Д(?ср выделяет целый класс процессов с одинаковым палучением акустической энергии областью о. Для фактического вычисления потока акустической эпсргпн -4s = Лх является безразличным, какой из конкретных процессов этого класса рассматривается»
Поэтому конкретизируем измепепия бр штутри а следующим образом: Ьр1 = Ьр= 6р2. Тогда, согласно (11.18) (при р = 0), последний член правой части равенства (11.19) дает после интегрирования пуль н поэтому суммарный поток акустической энергии для первого элементарного процесса представится в виде г
[bQ + biQWji-QWJz)]*^
О
Т
BPdbv]dt
Ї 6 а
Поскольку вдоль области a 6/j = const, имеем: ^ бр dbv = bp (6t>2 — bVj),
Ст
Что приводит к равенству
Т т
О о
Последнее выражеппе паипсано с помощью условий (11.11).
Физический смысл полученного соотношения весьма
Прост, Величина ЬЕ = — (bv2 — 6аА) характеризует колебательную составляющую процесса расширения некоторого объема, поресекающего о, a bp является колебательной составляющей давления в малой окрестности а. Поэтому величина Ах есть средняя работа расширения, сообщенная системе в процессе колебаний. Она будет положительной, еслп сдвпг по фазе между ЬЕ и bp пе
Превышает ~ по абсолютной волпчипе. Последний вывод следует из формулы
Л = ^ | ЬЕ ‘I bp I cos ti, 1
Где —фазовый сдвпг между ЬЕ и bp, (12.2) получается совершенно так же, как (11.5).
Как уже говорилось, равенства такого тни а удобно записывать в виде скалярных произведений входящих в них векторов. В частности,
A^-^bpbE. (12.3)
Чтобы построить диаграмму областей устойчивости, воспользовавшись равенствами (12.2) или (12.3), поступим следующим образом. Пусть излучение акустической энергии из открытых концов трубы отсутствует. Как было

Рис. 17. Диаграмма границ устойчивости для первого элементарного процесса (потери отсутствуют).
Показано в предыдущем параграфе, вектор bv в этом случае перпендикулярен к вектору bp. Направим вектор бр по оси х (рис. 17), п вектор бр — по оси у. Так как б t’j может і го совпадать с bv2, то условимся наносить па диаграмму б*;,. Положение бЕ на этой диаграмме полностью определяется углом Hj)j. Что касается абсолютных величин бр, bv и ЬЖ, то они могут быть в известном смысле неопределенными — Действительно, если задача решается без формулирования начальных условий, то, как было указапо в § 8, решение не дает величии амплитуд. Это иол о же ни е можно уточнить в том смысле, что решение для каждой гармоппки получается с точностью до неопределенного множителя; — амплитуда колебаний
каждой гармоники остается неопределенной, хотя соотношения между амплитудами б/;, б у и других переменных определяются однозначно. Проиллюстрируем это извест — пее нз теории дифференциальных уравпепип обстоятельство простым примером. Пусть при § = в течепип расположен узел давления /? = 0. При заданной частоте р фупкщш Фі (Іі) и Фг(£і) (4.14) определены однозначно.
,, An Фа
Второе уравнение (4.13) дает при этом = ~<р ) • Следовательно, хотя амплитуды Ар и А0 остаются неопределенными, отношение между ппми определеио.
Таким образом, диаграмма, приведештая на рпс. 17, может быть построена с точпостыо до масштаба. Одну из величин можпо выбрать произвольно, другие же определятся одпозначно. Пусть, например, 6/?=1 и б р направлено по оси х. Тогда каждый из векторов 6v и ЬЕ будет иметь но только определенное паправление, но и определенную величину. Такая диаграмма удобна тем, что дает наглядное представлеппе об относительных величинах н фазовых сдвигах возмущенных параметров процесса.
(12./,)
Нанесем на диаграмму, построенную на рис. 17, границу устойчивости. Границей устойчивости будем называть годограф таких значений вектора ЬЕ, при которых колебания происходят с постоянной амплитудой. В рассматриваемом случае (отсутствие потерь) условия (И.9) п (11.10) примут следующий впд:
Ах = 0 — граппца устойчивости, Аг > 0 —неустойчивость, Ах < 0 — устойчивость.
Из равенства (12.2) следует, что грапицеп устойчивости будет ось у — правая полуплоскость диаграммы будет соответствовать значениям бЕ, которые возбуждают систему, а левая полуплоскость таким ЬЕ, при которых возппкшие колебания гасятся. Следует ігапоміштг,, что векторы 6р п 6t> будут перпопдикулярпы лишь при,4, = 0. Поэтому прп положениях когтца вектора бЕ в точках нлоекостп {ху), не лежащих на граппце устойчивости, вектор не будет более совпадать с осью у.
Соотношения (12.4), формула (12.2) и приведенная диаграмма позволяют следующим образом сформулировать условия возбуждения в первом элементарном процессе.
Прп 6Х = 0 (6^ = б/л,) п при отсутствии потерь акустической энергии система будет возбуждаться, если между ЬЕ и колебательпой составляющей давления Ьр
V _ Я
Фазовый сдвиг по абсолютному значению менее —; если абсолютное зпачеине этого сдвига заключено между и л, то колебапня будут гаспться.
Полученный результат является обобщением критерия Рэлея на случай движущейся среды. Дело в том, что фаза бЕ и фаза колебательной составляющей теплоподвода bQ совпадают лишь для пенодвпжиой среды. В неподвижной среде расширение нагреваемого объема, которое характеризуется величиной ЬЕ, точно следует за процессом виешпего теплоподвода бQ. Этот факт настолько очевиден, что пе нуждается в особом доказательстве. Поэтому для неподвижной среды можпо вместо ЬЕ брать bQ (если речь идет о фазовых сдвигах) и тогда приведенное выше условно возбуждения совпадет с критерием Рэлея. Для движущейся среды фазы ЬЕ и bQ могут отличаться. Это будет показано в следующей главе. Таким образом, сформулированные здесь условия возбуждения охватывают более общий случай, чем критерий Рэлея.
(12.5)
Найдем условия возбуждения в первом элементарном процессе для случая, когда потери акустической эпергнп R отличны от нуля, и, следовательно, область о постоянно излучает акустическую энергию для компенсации этих потерь. В таком случае вместо соотношений (12.4) следует написать:
А2 — Я — граница устойчивости, Ах > R — неустойчивость, Ах < R — устойчивость.
Взяв Лх по формуле (12.2) п положив |6jd[=1, получим для границы устойчивости
т. е. проекция вектора а{ЬЕ на ось х остается постоянной п равной 2R. Это дает диаграмму, приведенную на рпс. 18. Границей устойчивости является прямая, перпендикулярная к оси х и отстоящая от начала координат па расстоянии 2R.
Важным отличием подученной здесь диаграммы устойчивости от "диаграммы устойчивости, приведенной на рис. 17, является то, что теперь нельзя сформулировать условия возбуждепия, го — иоря лпшь о фазовых сдвигах между ЬЕ її Ьр. При и1 ЬЕ < 2R возбужденно вообще певозмоншо, независимо от фазового сдвига — фі (следует помнить, что речь идет здесь об относительных величинах a ft Е и R, так как при построении диаграммы принято [ Ьр | = 1).
Условия возбуждения в рассмотренном случае трудно сформулировать так же просто, как и при Я = 0. Поэтому приведем их в виде аналитических соотношений, воспользовавшись формулой (12.3).
При 6Х = 0 и потерях акустической эпергнп R система возбуждается, если ~-ЬрЫ£ > R; колебания гасятся, если Ьр ЬЕ < R.
Эта формулировка является наиболее общей для первого элементарного процесса.

Рпс. 18. Диаграмма границ устойчивости для первого элементарного процесса при наличии потерь.
В заключение следует обратить внимание на одну особенность возбуждения в первом элементарном процессе. Пусть колебательная составляющая теплоподвода bQ будет точно синусоидальной, а средний уровень суммарного теплоподвода Qn Fe изменит своего значепия после начала акустических колебаний. Тогда AQcp = 0 и вся энергия 7 Б. В, Раушенбах
на поддержание акустических колебаний будет заимствоваться из потока виутрепней энергии. Интересным является в данном случае то, что мыслим процесс возбуждения акустических колебаний теплоподводом, при котором внешний теплоподвод пе используется в качестве источника эпергин для поддержания колебаний. Такой процесс невозможен, конечно, в неподвижном газе.
Обратимся теперь к рассмотрению второго элементарного процесса. Поскольку изучение этого типа возбуждения акустических колебаний теплоподводом во многом будет аналогично проведенному выше, изложим соответствующие результаты более кратко.
Как уже говорилось, второй элементарный процесс характеризуется условием 6£ = 0 илн 6t»i = flu2. Для фактического вычисления потока акустической энергии в этом случае (обозначим его А2) конкретизируем измепепие 6v вдоль а следующим образом: = bv = 6а2. Тогда согласно формулы (11.17) два первых слагаемых в правой части равепства (11.19) дадут после интегрирования пуль и поэтому суммарный поток акустической энергии А^ = А2 будет равен
■г т
[ -^(т-т)] dt = T П SШЬр]dt
О о О
По условпго 6i> = const. Следовательно, т т
A^-^Ubp^dp^dvdt^^ ^dXbvdt. (12.6) о о
Последнее выражение написано с помощью условий (11.11).
Физический смысл полученного соотношения также весьма прост. Величина 6Х’= характеризует
Колебательную составляющую сопротивления, действующего на течение в области a, a 6v является колебательной составляющей скорости в малой окрестности о. Поэтому работа А2 является работой сопротивления. Возбуждение системы в рассматриваемом случае зависит от того, может ли переменное сопротивление дать поло — жительиую работу, пе обходимую для поддержания колебании.
Для вычисления потока акустической эпергии Л2 можпо написать формулы, аналогичные формулам (12.2) и (12.3):
А = 16Х||б^|со5ф3( (12.7)
(Здесь а|)2 — фазовый сдвиг ЬХ и би.)
Построим для второго элементарного процесса диаграммы областей устойчивости по типу рассмотренных выше диаграмм.
При отсутствии излучепия акустической энергии из концов трубы векторы Ьр и bv взаимно перпендикулярны; направив их так же, как па рпс. 17, получим диаграмму, приведенную на рпс. 19. В целях единообразия
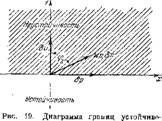
Сти для второго элементарного процесса (потери отсутствуют).
Эту диаграмму можно построить в масштабе Ьрх=> 1. Область устойчивости отделяется от области неустойчивости па основании очевидных критериев:
= 0 — граница устойчивости, Лг > О — неустойчивость, ^а < 0 — устойчивость.
(12.9)
Первое пз написанных здесь условий вместе с формулой (12.7) плп (12.8) показывает, что границей устойчивости является ось х, а второе условие (12.9) указывает на то. что положение конца вектора 6Х в верхней полуплоско с тп соответствует неустойчивому процессу.
Таким образом, условия возбуждения колебательной системы при реализации в зоне теплопровода второго элементарного процесса можно сформулировать следующим образом.
Прп дЕ—0 (bvl~6v.2) и нрн отсутствия потерь акустической энергии система буДот возбуждаться, если между 6Х и колебательной составляющей скорости 6v фазовый сдвпг по абсолютному значенню мепее у ; если абсолютноо значение этого сдвига заключено между Y и я, то колебания гасятся.
В том случае, когда суммарные потери акустической энергии R отличны от нуля, вместо соотношений (12.{J)
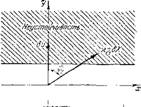
Устои
Рис. 20. Диаграмма границ устойчивости для второго элементарного процесса при наличии потерь.
Следует написать критерии, аналогичные (12.5). Онп дают следующие условия возбуждения для второго элементарного процесса: при 6£ = 0 н потерях акустической
Энергии R система возбуждается, если ЬХ Ьг> > R;
Колебания гасятся, если ~±6Xbv<R. При этой*
Диаграмма областей устойчивости примет внд, изображенный на рис. 20. Граница устойчивости пройдет параллельно оси х на некотором расстоянии от начала координат.



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике