В предыдущей главе было рассмотрено возбуждение колебательной системы при реализации элемептарпых процессов в зоне теплоподвода.
Рассмотрим в настоящем параграфе метод построения границ устойчивости наподобие тех, которые строились в § 12, но теперь для процесса в зопе теплоподвода, который не является элементарным. Однако предварительно получим некоторые следствия из найденных в настоящей главе выражений.
Прежде всего следует убедиться в том, что введепные ранее элементарные процессы в зоне теплоподвода могут реализоваться фактически, и поэтому проведенные выше рассмотрения пельзя считать отвлеченными теоретическими схемами.
Как следует нз формул (17.3) и (17.4), условия 6£ = 0 или ЬХ = 0 действительно могут быть реализованы. Пусть, например, заданы возмущения переменных перед зопоп теплоподвода vx, Pi и Эти три величины определят 6Х0, п для того, чтобы ЬХ обращалось в нуль, необходимо выполнение условия ЬХ’——ЬХ1У Таким образом, в зоне теплоподвода будет реализован первый элементарный процесс, если величина 6Х’ будет иметь вполне определенный модуль и аргумент. Это можно осуществить
самым различным образом, поскольку для получения нужного значения ЬХ’ можпо воспользоваться четырьмя независимыми параметрами: Jlf /2, /3 и Q. Если рассматривать для оиределешюстп простейший случаи возбуждения акустических колебаний в трубе Рийке-, то вдіє с го четырех свободных параметров сохранится лить (J* — безразмерное возмущение внешнего теплоподвода. Равенства (16.1) и (17.4) показывают, что первый элементарный процесс в трубе Рийке будет реализован при
7)*—
Вполне определенной колеблющейся составляющей теплоподвода. Точно такое же рассуждение можно провести и для обоснования реальности второго элементарного процесса (6£ = 0).
Вторым обстоятельством, которое нужно отметить, является то, что в движущейся среде фазы ЬЕ и колеблющейся составляющей теплоподвода Q ие совпадают. Действительно, рассматривая, например, простейшпй случай колебанпп в трубе Рийке, можно на основании формул (16.1), (17.3) и (17.4) написать
6E = &EQ-{-2blsM*Q*.
Поскольку фаза ЬЕ0, вообще говоря, не совпадает с фазой Q*, высказанное утверждение доказано. Это обстоятельство позволило рассматривать условия возбуждения, полученные в § 12 для первого элементарного процесса, в качестве обобщения критерия Рэлея (последний оказывается справедливым лишь при совпадении фаз ЬЕ н Q*).
Рассмотрим теперь некоторые свойства, которыми могут обладать процессы в зоне теплоподвода и которые позволяют во мпогпх случаях получать восьма наглядные диаграммы областей устойчивости.
Как уже указывалось выше, грапица устойчивости определяется равенством (11.9) = В общем случае из (13.2), вводя безразмерный поток акустической энергии по формулам
J=—; Л = (19.1)
У-а^Рх ка-іРі
1
As = ~ (і^б^-f і^ЬХ + ЬЕЬХ). (19.2)
Условие существовании границы устойчивости запишется в виде
(19.3)
Равенства (19.2) п (19.3) показывают, что при заданных рг и Vi существует сложная совокупность значений 6JE и ЬХ, удовлетворяющих условию, определяющему границу устойчивости. Этой совокупности трудно придать наглядность, так как связь между искомой величиной и двумя векторами сводится, как известно, к связи этой величины с четырьмя скалярными переменными. Кроме того, не следует забывать, что п величины рх и г?-, могут изменяться (при перемещении поверхности разрыва Z вдоль стоячей воліпл, возникшей в спстеме).
Анализ условии возбуждения обычно сильно упрощается в тех случаях, когда величины ЬЕ и ЬХ оказываются функциями одной и той же комплексной переменной, єсліі ие считать зависимости их от и sx. Приведем
Несколько примеров таких процессов в зоне топлоподвода.
В качестве первого прпмера рассмотрим все те случаи, когда процесс в зоне теплоподвода может быть представлен как процесс подвода тепла в некоторой области, неподвижной относительно стенок трубы и имеющей пренебрежимо малую протяженность в направлении осп трубы (труба Рнйке и т. п.). Малая протяженность области теплоподвода при условии ее неподвижности приводит к тому, что,/j =/3 = ,/3 = 0 и, следовательно, как показывают формулы (16.1) и (17.4),
ЬЕ’ = 2b13M2LQ*, )
![]()
В случае горепия вместо 2MQ* может стоять величина Q.
Получим
Вторым примером будет случаи постоянного теплоподвода на подвижной поверхности пламени. Как видно из
Формул (16.2), (16.3) и (16.4), /3, 72 и 73 будут фупк — 1 д т.
Дней величины которую можно представить
Как сумму vL и Ux или Uх офф. Таким образом, величины ЬЕ’ и ЬХ’ окажутся функциями v1 и возмущения эффективной скорости распространения фронта пламени относительно холодной смеси:
ЬЕ’ ^gev^ ЬЕи13фф, | ЬХ’ = axv1 + bxUl эфф, )
Где as, йх, Ье, — некоторые числеипые коэффициенты.
Величина V], вошедшая в формулы (19.5), не мешает считать ЬЕ’ и ЬХ’ функциями одной переменной £/1Эфф. Дело в том, что Vy (как и рх) обычно задается, кроме того, г входит в формулу (19.2) непосредственно и содержится в членах 6Х0 и ЬЕ0. Таким образом, свободным параметром, который можпо варьировать произвольно и влияние которого па устойчивость имеет смысл изучать, является комплексная переменная £/10фф.
В качестве третьего примера рассмотрим процесс, в котором как Jlt J2 и /3, так и т)СР и qY отличны от пуля. Пусть, например, в зону горения поступает смесь с перемеппым коэффициентом избытка воздуха а. Такая смесь будет характеризоваться отличным от нудя. Если предположить, что полнота сгораиия т]С1, однозначно определяется a, и plt и положение фронта иламепи, а следовательно, и Jlt /2 и /3 также являются функциями a, t)i и ръ то величины ЬЕ и ЬХ будут зависеть только от а, в том же смысле, в каком выше говорилось о зависимости ЬЕ и ЬХ только от £/"1Эфф.
Количество подобных примеров можно было бы увеличить. Для всех приведенных случаев анализ условий возбуждения упрощается потому, что зависимость As от одного комплексного параметра может быть хорошо представлена на плоскости. Это позволяет осуществить построение наглядных диаграмм границ устойчивости. Чтобы не быть связанным с каким-либо одним конкретным примером, будем рассматривать задачу в более общей постановке—будем считать, что величины ЬЕ и ЬХ зависят от некоторого комплексного параметра Y (безразмерного возмущения какой-то существенной величніш Y), а также от Рі п Cj. Формулы (17.4) показывают, что можно ожидать зависимости ЬЕ и ЬХ и от sx, но обычно течение в холодной части трубы, до пересечепия потоком воздуха ЗОНЫ теплоподвода НЗОЭНТрОПИЧНО и поэтому Sj = 0.
Следовательно, в рассматриваемом случае первые два уравнения (17.5) можпо записать в следующем виде:
Где aik — некоторые численные коэффициенты [отличные от обозначенных таким же образом коэффициентов уравнений (17.5)]. _
Вычисление Л2 по формуле (19.2) в рассматриваемом случае пе имеет смысла, так как соотношения (19.6) не содержат ЬЕ и ЬХ, выраженных непосредственно через Y. Воспользуемся поэтому формулой (13.1), которая при переходе к безразмерным переменным примет следующий вид:
Л2 — у (19.7)
Здесь, как и ранее, п — ~, т = .
% ад
Рассматривая входящие в равенства (J9.fi) переменные v, р и У как векторные велпчипы, возьмем скалярное произведение этих равенств друг на друга.
Р%*>2 = «ІІ^І^І 4- fif/^pl Н — anai3 У2 4-
+ (йыд22 + а]2а21) рхРг +
+ (anajs 4 «13я43) і?! У + (пІ2й, з + «13а,2) рТ.
Используя (19.7) и последнее равепство, получим пз (19.3) следующее соотношение, эквивалентное условию устой — чивоети:
Л У’2 Вр, Т-f CvjT+Dp* + FpLv} — R^ 0, (I’J.8)
Где А, В, С, D, Е и. F —численные коэффициенты,
1 п 1
= — nmav/i.2:}, D = — пта12а22,
Я = -1 пт (йх.,а.,3 -t-ff^rc^). Е = дтаиа21, С = ^ (аиЯгз + я13а21), ^ = у [лт (ЛцО^Н — а]2а21) — 1J.
Воспользуемся условием (19.8) для построения диаграммы граипц устойчивости. Построение начнем с наиболее простого случая, характеризуемого отсутствием потерь акустической энергии.
Пусть слепа и справа от зоны теплоподвода потери акустической энергии равны нулю (например, слева и справа от указапиой зоны расположены узлы скорости или давления). Тогда, как это было показано в § 11 при обсуждении формулы (11.7), векторы р и v должны быть ортогональны и поэтому = jp3?, = 0. Поэтому вместо равенства (19.8) получим
А Г2 + Вр^Г -1- Сг, У + Dp] + ЕЇ = 0. (19.9)
Границу устойчивости будем строить в прямоугольной системе координат (х, у). Пусть векторы рг, і и Y приложены к началу координат и вращаются вокруг него с частотой со (см. § 2). Выберем такой момент времени, когда вектор р, будет направлен по оси х, а ось у направим по вектору rv Вектор I" будет расположен некоторым произвольным образом относительно осей координат. Границей устойчивости в плоскости (х, у) будем называть геометрическое место концов векторов Г, удовлетворяющих (19.9). Введем обозначения для векторов Рх, vі и Y через их проекции на оси х и у. Опп будут выражаться следующим образом: (рг, 0); (0, Vx) (Yx, Yv). Запишем теперь сумму скалярных произведений (19.9) через проекции сомножителей;
^ (П + П) + Врг¥х + Cv, V„ + Dp’ + Evx = 0. (19.10)
Нетрудно видеть, что при заданных и vx уравнение (19.10) указывает па движение копца вектора Y но
окружности, положение и радиус которой зависят от рг и vv Следовательно, множество векторов У, возбуждающих колебания, отделяется от всех остальных па плоскости (х, у) годографом, имеющим форму окружности. Поскольку размеры и положение этой окружности изменяются с изменением рг и vv различным положениям плоскости теплоподвода 2 по длине трубы — ближе
Или дальше от узла давления, — или различным частотам колебаний, т. е. различным рг и i>, могут соответствовать различные границы устойчивости. Таким образом, условия возбуждения системы могут изменяться при изменении положения 2, или частоты колебания. На рис. 2(5 изображена граница устойчивости
Pi п 1»!.
У
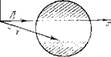
Для заданных Pi и vi
Vj
Рис. 26. Диаграмма устойчивости Для некоторых заданных
Ma основании проделанных выкладок можно ут вер-
Ждать только то, что при положении конца вектора У на изображенной окружности колебания будут нейтральными. Вопрос о том, по какую сторону окружности лежит область устойчивости, а по какую область неустойчивости, требует дополнительного исследования. В большинстве практических случаев не возникает необходимости проводить такое исследование, поскольку ответ бывает ясен из физпческой сущности задачи.
Однако апализ этого вопроса не представляет больших трудностей н в тех случаях, когда физические соображения не дают сразу очевидного решения.
Можно провести, например, следующее качественное рассуждение. Пусть величина Y такова, что процесс нейтрален. Сохраним значение рг и vx и изменим песколько Y (таким образом, чтобы конец этого вектора сошел с гра-
Ницы устойчивости). Тогда равенство (19.10) нарушится, причем, основываясь на рассуждениях, проведенных прп выводе уравнения (19.8), можно будет написать
А (УІ + ?l) + BPlYx + Cv1Yy + Dp + Az.
Прп отсутствии потерь в системе границе устойчивости соответствует А? = 0, > 0 дает неустойчивость, а < 0 — устойчивость процесса. В начале координат Yx = Yy = 0 н А% = Dpx— bvv Следовательно, еслп
Dp*±Ev*<Q, (19.11)
То процесс в окрестности начала координат устойчив, а значит неустойчив внутри окружности.
Условимся штриховать область неустойчивости. Тогда при выполнении неравенства (19.11) внутренняя часть окружности на рис. 26 будет заштрихована. Такая именно картина наблюдается, например, в тех случаях, когда акустические колебания возбуждаются теплоподводом, сконцентрированным в одной, неподвижной относительно стенок трубы плоскости (труба Рийке и т. п.).
Нестрогость приведенного здесь качественного рассуждения заключается в том, что при А% ф 0 колебания перестают быть гармоннчеекгши, приведенные выше формулы для потоков акустической энергии становятся неправильными, а угол между векторами рх и начи — jt
Нает отличаться от — у — .
Если стреїситься к более точному анализу, то это обычно проще всего сделать путем фактического вычисления декремента затухания колебаний для какой-либо точки диаграммы, например, начала координат. Соответствующие методы будут развиты в следующих главах.
Сравнивая полученный здесь и приведенный на рпс. 26 результат с рассмотренными в предыдущей главе условиями возбуждения в двух элементарных процессах, легко отметить усложнение условий возбуждения. Это усложнение выражается в том, что, во-первых, фазовые соотношения между Y и рх пли I’j пе могут быть сформулированы так просто, как для элементарных процессов;
Во-вторых, помимо фазовых соотношении, приходится учитывать и амплнтудпые, т. е. величину | Y и, в-третьих, условия возбуждения зависят от положения плоскости разрыва 2 по длипе трубы (от рх и vt). Следует заметить, что такое усложнение уел опий возбуждения не связано с переходом к параметру Y вместо ЬХ и ЬЕ. Рассмотрение задачи о границах устойчивости при заданных Pv vlt ЬХ Ф 0 и переменном ЬЕ (или при заданном ЬЕф О и переменном 6Х) показывает, что и при таком подходе фазовые соотношения усложняются, начинает играть существенную роль абсолютная величина переменного параметра (ЬЕ или б А’) и условия возбуждения становятся функцией положения плоскости 2 по длипе трубы (функцией Pi и с/,). Таким образом, в отлнчне от элементарных процессов (при ЬЕ пли ЬХ, равном пулю) все остальные процессы по своей физической сущности дают сложные условия возбуждения. Причина кроется в том, что в этих случаях происходит заимствование энергии из двух источников одновременно, что приводит к сложной картине их взаимодействия. Несколько подробнее этот вопрос будет освещен ниже.
Гравица устойчивости, изображенная на рпс. 26. получена в предположении, что значения рх и vx заданы. Однако здесь уже неоднократно подчеркивалось, что в зависимости от положения зоны теплоподвода нс) длине трубы (точнее, в зависимости от ее положения относительной стоячей ВОЛНЫ возмущения) значения р, И V! могут изменяться, а следовательно, б}гдет смещаться и изменять свои размеры окружность на рис. 26. Поэтому естественно поставить вопрос о нахождеппп семейства таких окружностей, соответствующих всем МЫСЛИМЫ)! для данной трубы значениям рх и vv
Здесь речь идет, конечно, не об абсолютных значениях и с,, а о соотношении между ними. Как уже говорилось, применяемый метод дает все величины С ТОЧНОСТЬЮ до масштаба.
Решение задачи о колебаниях в переменных и, w показывает, что при нейтральных колебаниях обе эти величины остаются постоянными по абсолютному значе — нию для любых сечений трубы, если между этими сечениями нет поверхностей разрыва. Такому условию удовлетворяет, в частности, отрезок трубы, по которому течет холодный газ. Поэтому можпо написать, что на этом участке
I Wj | = const, ] w, І = const
Пли
= const, u = const. Соотношения (4.9), связывающие переменные и. w иp, v, позволяют на этом основанпп написать: + Pi — const,
Vf — 2 v2Pi — f р* = const. Отсюда получаем связь между р и і’ в случае нейтральных колебаний
1І +" Р — const — Написав скалярные квадраты через проекции векторов, найдем
+ = const. (19.12)
Уравнение (19.10) показывает, что положепио центра окружности, изображенной на рис. 26, определяется координатами:
— 1 в ~ 1 — о ~л Pi>
ЛС_ (19.13)
Сравнивая равенства (19.12) и (19.13), можпо видеть, что центры окружностей уа) будут гіеремеїцаться но дуге эллипса. Надо лишь добавить, что центры (zQ, уа) будут располагаться пе на всей дуге эллипса, а лишь на одной из четвертей его дуги. Действительно, в выбранной системе координат рг и ц всегда положительны. Положение искомой четверти дуги эллипса зависит от знаков численных коэффициентов ^ и ~. Расчеты показывают, что, например, для случая возбуждения колебаний переменным тепЛОИОДВОДОЛІ (У = Q) этой четвертью всегда будет четвертая четверть.
Проводеииый анализ позволяет утверждать, что семейство всех границ устойчивости составлено множеством окружностей, центры которых перемещаются по четверти дуги эллипса. Огибающая этого семейства ограничит
Область, изображенную на рис. 27 (эта область построена для определенности применительно к случаю У=0. При попадании конца вектора Y в заштрихованную область возбуждение системы становится возможным.
Реализация этой возможности связана с тем, находится ли конец вектора Y внутри той из окружностей семейства, которая соответствует фактическому положению поверхности разрыва 2 (фактическим рх н flj). Внутри заштрихованной области может существовать подобласть, принадлежащая всем окружностям семейства. На рис. 27 она заштрихована в клетку. При попадании конца вектора Y в эту подобласть возбуждение становится возможным вне зависимости от положения поверхности 2 вдоль осп трубы. В этом смысле можно говорить о значениях вектора Y, прп которых, возбуждение особенно вероятпо. Положение конца вектора Y вне заштрихованных областей всегда соответствует устойчивости системы.
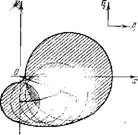
Рис. 27. Диаграмма устойчивости для произвольных pj ii vx.
Чтобы правпльно понимать смысл построенных диаграмм, укажем на одно важное обстоятельство. Каждая окружность — граница устойчивости—строилась для заданных, неизменных значений рх н vv Но это не означает, что все режимы, соответствующие точкам такой окружности, могут быть фактически реализованы в одной и той же трубе. Действительно, пусть режим колебапий, соответствующий одной из точек некоторой границы устойчи-
востп, реализован в трубе с областью теплоподвода, расположенной на расстоянии Ьх от входного конца п Ь2 от выходного. Примем, что на концах трубы расположены узлы давления. Перейдем теперь мыслеппо в соседнюю точку той же окружности — границы устойчивости. Тогда рх п vx не изменятся, а частота со не сможет измениться, так как иначе нарушится краевое условие па входе. (Это видно, например, из формул (4.13) и (4.14).) Таким образом, при переходе в соседнюю точку границы устойчивости процесс колебаний во входном участке пе меняется. Перемещение но окружности границы устойчивости означает в этих условиях только изменение вектора У".
Как видно из уравнений (19.6), изменение Y при непз менных р1 И vx неизбежно приводит к изменению р., И Vc,. Поскольку размерная частота колебаний одинакова для обеих частей трубы, частота колебаний в горячей части трубы не может измениться. Но тогда функции ц>х и ср2 для горячей части тоже останутся неизменными и краевое условие па выходном конце нарушится в енлу изменения величии р2 и 1?2 в плоскости теплоподвода [величины Av и Л в равенствах (4.13)]. Чтобы сохранить краевое условие па выходе, необходимо изменить длину Ьг. Таким образом, двигаясь по окружности границы устойчивости, приходится мысленно изменять какую-либо характеристику трубы, например длину Lv
Этот страппый, па первый взгляд, результат вполне естествен, так как при построении граппц устойчивости были использованы только энергетические соображения и краевые условия никак не оговаривались.
Еслп краевые условия заданы, то при измен сипи У будут меняться не только р2 и i? a, но ирj. и частота колебаний, а граппца устойчивости для подобной трубы фиксированных размеров будет составляться точками, принадлежащими разпым окружностям уже найденного в настоящем параграфе семейства. При этом область неустойчивости окажется внутри заштрихованной части диаграммы па рис. 27.
В заключение следует обратить внимание на вид грапиц устойчивости рассматриваемого тина в тех случаях, когда плоскость 2 находится точно в узлах скорости плп давления. Следует, правда, оговориться, что термин «точно» имеет смысл лишь для элементарных процессов, так как в общем случае возмущенно давления или скорости при
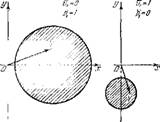
Рис. 28. Диаграммы устойчивости при положении плоскости теплоподвода 2 в узле скорости и узле давления.
Пересечении области теплоподвода а пе остается неизменным. Если условиться считать положением плоскости 2 в узле совпадение ее с сечением, Где /.>!= О или ut= О, то соответствующие границы устойчивости займут, согласно формул (19.13), положения, указанные на рнс. 28. Слева дана диаграмма для положения Z в узле скорости, а справа — в узле давлеппя.



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике