Настоящий параграф посвящен рассмотрению диа­грамм устойчивости для некоторых типичных случаев. Основной задачей будет анализ изменения конфигурации граииц устойчивости в зависимости от особенностей про­цесса теплоподвода в зоне а. Однако прежде чем переходить к такому апализу, сделаем одно замечание.

Приведенная на рис. 27 диаграмма является характер — ной для случая возбуждения колебаний теилоподводом

(У = 0. Следует отметить интересную особенность такого случая — начало координат пе попадает в заштрихован­ную область. Это означает, что для возбуждепия системы надо иметь конечное значение вектора Q-, при Q, по абсо­лютному значению меньшем некоторой величины, система вообще никогда не возбудится. Следует подчеркнуть, что конечность Q не означает необходимости конечного воз­мущения теплоподвода в начальный момент времени. Дело в толі, что прп построении диаграмм типа приведенных на рпс. 26 и 27, значение суммы v]-~р условно прини­мается равным единице, подобно тому, как это делалось при построении диаграмм устойчивости для элементарных процессов. Следовательно, в общем случае, говоря о вели­чине Y, следует понимать, что речь пдет о соотношении между величиной Y и величиной, принятой за единицу. В начальный момент, когда истпппая амплитуда возму­щения давлення (условная единица) мала, тот же порядок малостн имеет, очевидно, и Q.

Рассмотрим теперь несколько частных случаев диа­грамм устойчивости. Построенная па рис. 27 диаграмма соответствует возбуждению колебаний при /j = /2 = /3 = 0, т. е. за счет одного лишь возмущения теплоподвода Q. Она построена для самого общего случая. Предположим, что в установившемся движении подогрев газа при пере­сечении им поверхности 2 пренебрежимо мал, так что в уравнениях (15.7) — можно положить^ =М„ = Л/ = а2; это соответствует в первом приближении возбуждению звука в трубе Рийко. Тогда систему (15.7) можно запи­сать в следующем виде:

Щ + Мр2 — МЇ2 = + Мрг — МІг, 2Mv2 + (1 + М2) р2 — М% =

= 2Mvx + (1 + М*) __ А/2" + ДГ2р* + м (л/2 + Р, — М-% + 0,

(20.2)

1

Где для трубы Ринке

Q = 2Мз()*.

Полная симметрия левых и правых частей уравнений. (20.1) (с точностью до слагаемого Q и при Р* = 0) дела­ет исключение переменных чрезвычайно простым. Не­сложные алгебрапчеекпо выкладки позволяют получить:

(20.3)

Сравнивая полученные равенства с равенствами (19.6), вндпм, что aJ2 —с?21 = 0, а это приводит в уравнении (19.8) к D-=E — 0. Но равенство нулю D и £ указывает, что окружность, определяемая уравнением (19,10), всегда проходит через начало координат. Таким образом, при малом подогреве в области о все окружности, являющиеся границами устойчивости, пересекаются в одной точке, и эта точка является началом координат. Соответству­ющее построение приведено на рис. 29, б, причем для полноты картины рядом (рис. 29, а) приведено такое же построение для случая конечного подогрева (ЛУ1<Д/2), аналогичной диаграмме на рис. 27. Сравнение диаграмм а и б указывает, что при малом подогреве система стано­вится ліеиее устойчивой в том смысле, что возбуждение ее возможно сколь угодно малыми относительными возму­щениями теплоподвода Q*.

Рассмотрим, наконец, третий случай из этой серии. Пусть М, = М„ = 0, т. е. в основном дпиженнп газ непо­движен. Тогда уравнения (20. о) дают

(20.4)

Теперь в уравнении (19.8) в нуль обращается А, С, D и Е, а уравнение окружности (19.10) вырождается в прямую Уж = 0, т. е. границей устойчивости становится ось у вне зависимости от и vt. Этот вид диаграммы границ устойчивости показан на рис. 29, в. Очевидно,
последний "случай является случаем Рэлея, поскольку система возбуждается, если фазовый сдвиг между воз­мущенной составляющей теплоподвода Q и периодической

Составляющей давления р, менее — у. Этот результат можно

Было предвидеть, поскольку второе равенство (20.4) ука­зывает на реализацию в рассматриваемом случае первого элементарного процесса.

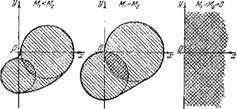
Ряс. 29. Влияние скорости течения на конфигурацию границ устойчивости.

A) ft BJ

Если сравнить три типа диаграмм устойчивости, приве­денных на рпс. 29, то, рассматривая их в обратном поряд­ке, можно видеть, как усложняются условия возбуждения сначала при возникповешш теченпя, а затем при сильном стацпопарном подогреве. При этом область, заштрихован­ная в клетку, все более уменьшается, т. е. наряду со свой­ствами процесса теплоподвода все большую роль начинает играть и положение плоскости 2 относительно стоячей волны, образовавшейся в трубе.

Путем построения аналогичных диаграмм устойчиво­сти для того типа теплоподвода, при котором фронт пла­мени свободно колеблется вместе с течением, можно пока­зать, что при подвижном фронте теплоподвода колеба­тельная система в известпом смысле более склонна к воз­буждению. Обратимся с этой целыо к системе уравнсптш (16.12). Исключив из левых частей этой системы s2 и учтя, 11 в. в. РаушснОах

ЧТО В ХОЛОДЦОМ течении 5] = 0, придем к спстеме аз двух уравнений, содержащих ув, p.,, v^ u Uv Если исклю­чить из них г?2 и при этом учесть формулы (15.9) и (15.10), ТО петрудпо убедиться, ЧТО коэффициент при 1>J в уравне­нии, определяющем/^, обращается в пуль. В обозначениях (19.6) это означает д2] = 0, что приводит в уравнениях (19.8) п (19.9) к Е = 0. Но тогда при рх = 0 граница устой­чивости проходит через начало координат. Сравнивая этот

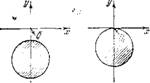
Рис. 30. Диаграммы устойчивости при воз- оуждешти системы теплоподводом И подвшк — ным пламенем (р1 = 0).

Случаи с рассмотренным выше (рис. 30), можпо видеть, что возбуждение акустических колебаний за счет подвижности фронта пламени (С/,) более вероятно, чем за счет колеблю­щегося теплоподвода (Q). Следует, правда, отметить, что это различие представляет скорее академический, чем практический интерес.