В отличне от задачи, рассмотренной в предыдущем параграфе, поток акустпчоской энергии, излучаемой областью теплоподвода а, не будет равен потоку эпоргии того же вида, возвращающемуся в область сг после отражения акустических воли от концов трубы. Поэтому в среднем за цикл колебания будет наблюдаться течение акустической энергии от области а к концам трубы. Аналитически это выразится в том, что амплитуды и и w перестанут быть равными друг другу.
В § 30 приводились формулы для учета потерь, связанных с излучением акустической энергии из открытых концов трубы. Там, в частности, был введен коэффициент £ (определенный равенством w = использование которого вместо пмпеданца z целесообразно при решении задач в координатах (и, w). Прп излучении акустической энергии во внешнее пространство, средний поток ее направлен в положительную сторону оси х в горячей части трубы и в противоположном паправлепии в холодной части трубы. Поэтому, вспомнив выражение для потока
акустической энергии (30.7), будехм иметь l^^l,
После сделанных здесь вводных замечании нетрудно построить методику расчета для рассматриваемого в настоящем параграфе случая. Ход решения задачп мало чем отличается от того, который подробно описан в предыдущем параграфе. Все отличия, которые следует иметь в виду, являются следствием новых краевых условий. Прп нахождении углов уі и Va между векторами н01 и w01; нц2 и ш02 нельзя пользоваться формулой (41.3), которая получена из предположения, что и и ш на концах трубы совпадают. Равенство
W = tu (42.1)
Показывает, что они, вообще говоря, сдвинуты на некоторый угол 0, который можно определить пз соотношения (30.5):
= arctg ( — t ) ,
Где г и х — вещественная и мнимая части нмпеданца Z = J’ IX. При этом следует иметь в виду, что знак числителя стоящего справа выражепня, пропорционального sin 0, определяет четверть, в которой лежит угол 0.
Таким образом, вместо формулы (41.3) надлежит пользоваться следующей:
Точно так же, прп переходе к равенствам, пе содержащим угла а и величин ш01, »02, ш02, вместо условий I Koil= I ">ot I и 11іо2І ~ І шо21 надо пользоваться следствиями новых краевых условий вида (42.1):
Кі!1м!"01!’} («-з)
КаІЧЄгІКаІ. J
Причем величина легко находится пз формулы (30.6).
Кроме того, фазовый угол 6q относительно м01 при отсутствии запаздывания (д = 0), обозначенный выше
24 в.
Через р, не будет более равен я + , поскольку вектор bv
В. Раутенбая
Не будет располагаться по биссектрисе угла у|. Из рпс. 85 видно, что теперь р = я + 7р где
. I Ci I sin v,
І (отсутствие потерь на концах) угол у, coll 2
V, = arclg, іv і—-— •
При
Впадает, как это и следовало ожпдать
Опуская громоздкие выкладки, напишем окончатель — пую систему уравнении, соответствующую системе (41.5)
!/

Рис. 85. Определение направления вектора bq при наличии потерь.
С учетом равенств (41.6), (42.2) и (41.9) для рассматриваемого численного примера: и01 [0,000508 | (1 + cos Yl) cos (у, + y[) —
— 0,00106 (1 + cos Yl) cos = — 0,385 4- + 0,792 I £ J cos Yl — 2,58 |»2 (1 + cosYl) cos YJ —
0,583 I Ј21 cos Ya +0,175 IE! J It. I cos (Yl + y2) +
+ l,24|?2|V2(l + coSYl)cos (Ys+Y;). 424
И01 [0,000508 |(1 +cos Yl) sin (Ys + Y;)- ( ‘
0,00106 (1 + cos Yl) sin Yl"] = 0,7921 ] sin Yl —
2,58 j/ 2 (1 + cos Yl) sin yl — 0,583 11, sin y2 +
+ 0,175 I tj 11 1 sin (Yl + y2) + + 1,2411 V2 (1 + cos Yl) sin (Ya + YJ).
Приведенная система решалась графически путем построения кривых гг01 = C0j) и и01 = /2 (Wj) аналогично тому, как это делалось в предыдущем параграфе. Расчеты..гі, ,
Велись для разных отношенпи — j — (а—-диаметр труоы,
L — ее длина), которые, как это видно пз формулы (30.8), определяют потери на излучение.
Результаты расчетов для трех первых гармоник приведены на рис. 86. Наиболее четко влияние потерь на
1-я гармот/са 2-я гармоника 3-я гармамша
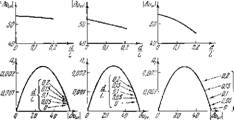
Рпс, 86. Амплитуды автоколебании бг'(111 при разлитых потерях эпергии па излучение (параметр d/L).
Характеристики автоколебаний видно па примере третьей гармоники, поскольку потерп увеличиваются пропорционально со2. Значения углов fr, для которых производился расчет, были следующими: для первой гармоники fr = 270°, для второй fr = 90°, для третьей # = 0°. Эти углы соответствуют полученным в предыдущем параграфе областям самовозбуждения. Частоты колебаний здесь не приводятся. Онп почти не изменяются после введения в расчет потерь на концах; наблюдается лшнь незначительное уменьшение частот автоколебапий.
В верхней части рпс. 86 дано изменение амплитуд колебания скорости |6у01|=Л(1 в функции Как видно из хода кривых, увеличение (увеличение потерь) сопровождается некоторым уменьшением амплитуд установившихся колебаний скорости.
В нижней части рпс. 86 приведены графики принятой в расчете зависимости А2 = f (AJ, на которых помочепы точки, соответствующие найденным амплитудам колебаний скорости. Эти графики показывают, что если при отсутствии потерь = значение Av а следовательно и колебательной составляющей тепловыделения б (/близко к нулю, то при наличии потерь (—-^О^она быстро возрастает, особенно для третьей гармоники. Результат этот вполне естествен, поскольку для принятой схемы процесса в области о только достаточно большая колебательная составляющая теплоподвода способиа осуществить восполнение потерь акустической энергии на концах трубы.
Интересно отметить, что при достаточно больших потерях величина амплитуды колебательной составляющей скорости |6i>01| становится меньше у0 = 50 м/сек, т. е. явление заброса пламепп против потока, о котором говорилось выше, может не наблюдаться. Правда, чтобы это произошло, труба должна быть достаточно «короткой».
Из этого следует, что в некоторых специальных случаях можно путем увеличения потерь получить вибрационное горение без заброса пламени
При достаточпо больших потерях возбуждение некоторой заданной гармоники может оказаться вообще невозможным. В рассматриваемом численном примере этому соответствует факт сужения диапазона значении fr, для которых возможно возбуждение автоколебаний по мере увеличения параметра Так, для третьей гармоники
Системы прп ~ = 0 возбуждение было возможным (прп принятых в расчете значениях д) для О = 330°, 0°, 30", 60° и 90°. При -^- = 0,2 автоколебания становятся возможными лишь при ft = 0° и 30°, для 0 = 330°, 60° и 90° система (42.4) решений не имеет.



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике