Большое число механизмов обратной связп, описан­ных в гл. VII, н возможность перехода от одного меха­низма возбуждения к другому в одном опыте, о котором шла речь в предыдущем параграфе, ставят вопрос о за­кономерностях, определяющих механизм возбуждения и поддержания колебаний в каждом конкретном случае.

Совершенно ясно, что условия опыта определяют неко­торое множество вероятных механизмов обратной связи.

Так, если происходит горение однородной и заранее под­готовленной смеси, то механизмы, связанные со смесе­образованием, не смогут проявиться. Однако такие огра­ничения (если опи существуют) все же оставляют доста­точно большое число вероятпых механизмов обратной связи.

Более того, если даже известен олшдаелшй механизм возбуждепия, то почти всегда остается открытым вопрос о том, каковы будут амплитудные и фазовые соотношения между колебаниями газовых масс и процесса горения. Как правило, эти соотношения расчету не поддаются. Действительно, очепь трудно, например, рассчитать фазу отрыва вихря в подводящем канале и его размеры. Если и можно рассчитать, папример, фазу колебания состава смеси к моменту подхода ее к стабилизаторам, то учесть все многочислепные факторы, от которых зависит воспла­менение этой смеси, сейчас невозможно. Невозможно рас­считать все периоды индукции, предсказать видоизме­нение конфигурации поверхности иламепи и т. д. Таким образом, на пути предсказания вероятности вибрацион­ных режимов работы двигателя или камеры сгорания встают серьезные трудности.

Однако, с другой стороны, множественность вероят­ных механизмов обратной связи и большое число «степе­ней свободы» у процесса горенпя (в том числе возможность возбуждения колебаний с различными частотами), делаю­щих возможными реализацию самых различных соотно­шений амплитуд стоячих волн и фазовых сдвигов между процессом колебания газов и горением, могут облегчить задачу прогноза вибрационных режимов и указать на эффективные меры их подавления. Дело в том, что оба указанных обстоятельства (большое число возможных механизмов обратпой связн и большая свобода в реали­зации амплитудных и фазовых соотношений) позволяют колебательной системе как бы выбирать механизм само­возбуждения и амплитудно-фазовые соотношения.

В этой связи можпо выдвинуть следующую гипотезу: в процессе развития вибрационного горения колебательная система стремится реализовать такой механизм возбуж­дения и такие амплитудные и фазовые соотношения, которые дают в конкретных условиях опыта максимум величины акустической энергии излучаемой областью горения.

Сформулированная здесь гипотеза может быть пояс­нена следующим образом. Пусть одновременно существует множество различных возможных механизмов возбужде­ния, причем каждый пз них имеет известную свободу в реализации амплитудно-фазовых соотношений. Тогда тот из них, который в конкретных условиях опыта дает наибольшую секундную работу обгонит в своем раз­витии остальные и в конце концов станет решающим ме­ханизмом возбуждения для данного конкретного случая.

Приведенное пояснение дает возможность указать на одну существенную деталь: очевидно, здесь ндет речь об отборе механизмов возоуждения но нрнзнаку .А^—-^шах в процессе разгона колебаний. Когда колебания установи­лись, величина потока акустической энергии опреде­ляется потерями. При этом предполагается, что к моменту установления колебаний процесс, дающий в условиях

Опыта /12=-4шах» уже усиел обогнать в своем развитии другие возможные процессы.

Надо отметить, что выдвинутая гипотеза предпола­гает отсутствие (ггли малость) потерь акустической эпер­гии. Если потерями пренебрегать нельзя, то прпведепная выше формулировка требует уточнений. При наличии по­терь нельзя просто говорить о наибольшем потоке энер­гии генерируемой в области теплоподвода, а следует нз этого потока вычитать указанные потерн. В связи с этим получим следующую уточненную формулировку гипотезы о максимуме акустической энергии: колебатель­ная система стремится реализовать такой процесс, кото­рый в конкретных условиях опыта дает максимум вели­чины акустической энергии, излучаемой областью горе­ния, за вычетом потерь.

Приведенное уточнение является совершенно необхо­димый!, так как иначе из предложения о стремлении колебательной системы реализовать условие As=Aшах следовало бы, что система должна стремиться осуществить процесс с наибольшими потерями, поскольку наиболь­шим потерям соответствует наибольшее значение в установившемся режиме колебаний. Ниже, при рассмот­рении пекоторых теоретических положений и при анализе опытных данных приведенное уточнепие но использует­ся, поскольку всюду делается предположение об относи­тельной малости потерь.

Рассмотрим некоторые следствия из гипотезы о макси­муме энергии Пусть характеристики процесса гореипя (величины бЕ и 6.Х) будут функциями одной и той же не­ременной, способной менять фазу п амплитуду, напри­мер, теплоподвода Q* или эффоктивпой скорости распро­странения пламени Uv пли какой-либо другой величины. Тогда можпо, чтобы ие быть связанными конкретной за­висимостью ЬЕ и ЬХ от одной из названных величии, ввести, как и в § 19, неременную Y, записав условия, связывающие колебания слева и справа от зоны теплопод­вода в виде равенств (19.6):

(45.1)

Если привести ути зависимости к каноническому виду (17.1), то их можно будет записать следующим образом:

(45.2)

В приведенной записи произведен переход от комплекс­ных переменных к векторным, а одинаково обозначенные вещественные коэффициенты преобразований (45-1) и (45.2), конечпо, отличаются друг от друга.

Связь между коэффициентами преобразований (45.1) и (45.2) весьма проста п находится в процессе числеп — ного приведения равепств (45.1) к каноническому виду. ІІпже в настоящем парагафе будут всюду использоваться коэффициенты преобразования (45.2).

Пусть фазовый сдвиг между г и pt будет -у, т. е.

Г^! —0. Это предположение соответствует случаю, когда средний поток акустической энергии в холодной части
течения равен нулю (например, прп схеме процесса, изображенной на рпс. 3’1).

Найдем для этого случая, воспользовавшись форму­лами (19.2) и (45.2), поток акустической энергнп, излу­чаемой зоной теплоподвода:

■Ті ^ 1: + + ftЈ (VY) = T 1 + a**№ 4

+ [а2Я (1 + яп)Н-а21аі8]VjYH-ais^s^2)- (45,3)

Поскольку фазовый сдвиг между рх и vx равен, то

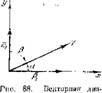
Удобно перейти к диаграмме того же типа, что и пред­ставленная на рнс. 26. Для рассматриваемого случая она дана на рис. 88. Если обозначить проекции вектора Г па оси х и у через Yx и У, то выражение для (45.3) примет следующий вид:

= {{«12 (1 4- 4 «21 (1Н — «11Ї v 4

4 [«13 (Н — «02) 4 «іаМ РіУХ + [«23 (1 +«jj) 4 «21«І. і] ^y-l — 4 «ізй23 4 Уу)}- (45.4) Здесь pv vvYx и Уу —скалярные (вещественные) вели­чины; первые две являются абсолютными величинами векторов И поскольку эти векторы но условию всегда направлены но осям х и у.

Сделаем теперь наиболее простое предположение о пол — поп независимости У2 от рх 11 l’i л найдем такие значе­ния У, которые соответствуют максимуму Для этой

ДЛ? дЛ2

Цели приравняем нулю производные _~ н —.

&¥х OYy

__ Несложные вычисления дают искомые значения Ух~Ух0′ Yv = Yvo> соответствующие Л2 = УІтах:

Т? _ __ йіз(14°аг)-1-Діабаз ~ х0~ 2аіаа2* Рї

У _ »23(^4<7n) + fli3«2I "

~ Ji

" 13 23

25 Б. В. РаушенЛах

Формулы (45.5) указывают, что если предположение об Л2 = Лшах справедливо, колебательпая система будет всегда стремиться иметь Г", лежащие в одной четверти диаграммы, представленной на рис. 88. Действительно, поскольку рг и но условию всегда положительны, то вне зависимости от их величины знаки Уя0 и Уу0 пол­ностью определяются выражениями, СТОЯЩИМИ перед Pi и а следовательно, определяется и четверть, в кото­рой расположен вектор Y. Числепные расчеты показы­вают, что для Y = Q* и Г = исгор (где Ucr0p — безраз­мерная вариация скорости распространения фронта пламени, отличающаяся от lfL знаком), такой четвертью является четвертая.

Следовательно, хотя диаграммы границ устойчивости (рис. 27) указывают на возможность возбуждения коле­баний при У, лежащем в первой, третьей и четвертой чет­вертях, в случае справедливости высказаппой гипотезы колебательпая система будет стремиться реализовать только последний случай.

Полученные для Уж0 л Уи0 формулы (45.5) требуют знания р1 и vv Однако и эти величины, быть может с большим оспованием, чем Yх и Yу, колебательная система способна «выбирать», сообразуясь с условиями возбуждения. Действительно, соотношение между рх и vx определяется положением сечения теплоподвода 2 отно­сительно стоячей волны, образовавшейся в холодной части течения. Последнее же определяется не столько геомет­рическим положением 2 по оси трубы (оно обычно задано), сколько номером возбуждаемой гармоники. Найдем поэтому соотношение между Pi и Vlt которое соответствует Лх = Атах и предполагает, что условия экстремума (45.5) уже выполнены.

В рассматриваемом случае рх и vx связаны усло­вием (19.12). Входящая в это соотношение постоянная определяет амплитуды колебаний; обозначим ее с2, т. е. положим

(45.6)

Формулы (45.6) и (6.3) показывают, что можпо написать такие выражения для vL и

(45.7)

Где <р—некоторый свободный параметр. Найдем <р, при котором As принимает экстремальное значение. Физически это озпачает, что ищется определенное соотношение между и Vi в сечении, і "до расположена плоскость теплопод­вода 2. Реализация этого соотношения возможна лишь при возбуждении соответствующей гармоники; таким образом, по сути ищется та гармопика, возбуждение кото­рой даст максимум потоку энергии

Здесь следует заметить, что задание ф (т. е. задание /?, и и,) определяет номера гармоник лишь в том случае, если одновремеппо задано краевое условпе на левом конце трубы. Но не следует забывать, что надо, кроме того, удовлетворить еще краевому условию на правом конце. При заданных свойствах поверхности теплоподвода 2 и при ограниченном числе гармоник, которые фактически могут быть реализованы, среди: найденных гармоник может не оказаться такой, которая одновременно точио удовлетворяла бы и краевому условию на правом копце. Поэтому все последующие рассуждения справедливы для реальных систем лишь в первом прпб^шжешш. Они дают тенденцию поведения колебательпой системы, а не точное решение краевой задачи. Это замечанпе следует постоянно иметь в виду при чтении настоящей главы.

(45.8) 25»

Если подставить значения Уж0 и У 0 (45.5) в выра­жение (45.4), то сразу находится следующая формула для

Jz = CilA — г c2vl

Где Cj и е., — некоторые вещественные коэффициенты. С учетом выражений (45.7) последнее равенство можно записать так:

Ле = с2 (с, COS2 ф + c2sin2cp).

«•’І*

ВзЯ! і производную — — и приравняй ее пулю, найдем

Значения ф, которые соответствуют экстремумам Лv. Легко

^ n Jt Зл

Видеть, ЧТО еслп Cj ф Со, зто оудут — J — , Л, .

Поскольку по условию ^ п не могут быть отрицатель­ными величинами, у і-о л ф дол жоп удовлетворять соотно­шению 0 < откуда следует, ЧТО ПОТОК энергии УІ2

Достигает экстремальных значении только при гр = 0 л

И <р=-2 .

Численный анализ, произведенный для типических значений коэффициентов преобразований (45.2), показал, что максимуму А? соответствует ф=0. Таким образом, еслп колебательная система имеет возможность свобод­ного выбора как величины ц фазы Y, так и номера возбуждаемой гармоники, она будет стремиться реали­зовать такой процесс, при котором фазы Y и рг будут совпадать 1). Этот результат в какой-то мере напоминает гипотезу Рэлея, хотя, но-существу, имеет совершенно иное содержание.

Надо сказать, что возможность свободного выбора величины и фазы Y, а также номера возбуждаемой гар­моники свойственна далеко пе всем реальным процессам горения. Скорее это надо рассматривать как исключи­тельный, предельный случай. В реальных процессах амплитуда Y может быть ограничена физическими свой­ствами явления, которые не позволят достигнуть теоре­тически «оптимального» значения Y, а фаза Y может оказаться связанной, например, с колебанием скорости. Наиболее четко это прослеживается для трубы Рийко, в которой теплоотдача от нагретой сетки к воздуху однозначно определяется частотой н амплитудой коле­бания скорости воздуха, обтекающего элементы сеткп,

Последнее следует, jiiinpusii’iu и.-і рцлелств (45.5). При f = 0 Vi=0 л, следовательно, У,/() = 0, т. е. направление Виктора Г совпадает с направлением р{.

И но может быть «выбрана» системой каким-либо ииым образом.

Процессы сгорания плюют, копечно, зпачптельио больше «степеней свободы», чем теплоотдача от сетки, поскольку горение зависит от скорости течения, от различных периодов индукции, процесса вихреобразования и многих дру­гих взаимно независимых пара­метров. Однако п здесь может не наблюдаться полной неза­висимости Y от процесса коле­баний.

Чтобы показать, как в та­ком случае будет вести себя колебательная система, рас­смотрим следующий пример. Пусть возбуждение происходит вследствие подвижности фронта пламени, которая предполагается зависящей от колебания скорости потока. Допустим, для простоты, что эта зависимость может быть выражена линейным соотношением | Y | = Ь v Чтобы учесть возможное запаздывание, введем сдвиг по фазе между Y и vv рав­ный углу (5 (рпс. 88). Тогда очевидно

Ух = Ь Sin [Ц; Yy = Ь cos fj (45.9)

^ = оЙ — г Ч-і — — і — а4Ъ, Уу + о5 (У* + У£), (45.10)

Где коэффициенты alf а2, . .., а. находятся из сравнения написанного равенства с равенством (45.4). Использовав формулы (45.7) и (45.9), придадим соотношению (45.10) форму

Az

= cos2 ф + a3b sin (5 sin ср cos ф — f

-f («2 + я4 b cos.(З + аф’1) sin2 ф. (45.11)

Грамма для расчетного при-

Если допустить, что зависимость Y от процесса акустических колебапий задана, т. е. заданы & п р, то колебательная система сохранит возможность выбора номеров гармоник, которые в рассматриваемом случае
определяются углом <р. Найдем значения ф, удовлетворяю­щие условию А^ = Атах, для различных фиксированных зиаченвй Ь и р. Поскольку масштабная постоянная с не может повлиять на искомый результат, положим се

DA*

Равной единице. Приравняв нулю производную > найдем соотношения, определяющие ф, соответствующие экстремуму As’.

Tg 2ср ^ІІіР—^ . (45.12)

Условие максимума < 0 даст неравенство

(а0 — ci-l — j — a4b cos (5 + abb~) cos 2ф — a^b sin p «in 2qj < 0,

(45.13)

Позволяющее отделить ф, соответствующие максимуму от ф, соответствующих минимуму этой величины.

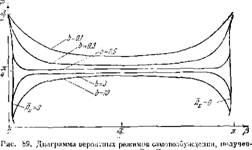
Воспользуемся полученными формулами для численного расчета типического случая, характеризуемого Мj=0,1; Л/2=0,25. Пусть возбуждеиие колебательной системы происходит за счет подвижности фронта пламени, кото­рую будем выражать через Ucгор — Тогда зависимость цз от р, при разных by удовлетворяющая условию может быть представлена семейством кривых, изобра­женных на рис. 89. Указанное семейство построено для всех практически интересных значений (3, изменяющихся от 0 до я. Пределы изменения величины b взяты от 0,1 до 10. Чтобы оценить вероятные численные значепия коэф­фициента Ь, проведем такое рассуждение. В рассматривае­мом примере Y= f7"m, p, следовательно | t-‘crop ~bvv При установившемся режиме гореипя £/СГор — і т — эффек­тивная стационарная скорость распространения нламенп численно равна установившемуся значению скорости те­чения. Если допустить, что и вариации этих величин имеют один порядок, то вероятное значение коэффициента b должпо быть близким к едпнице. Диапазоп изменения b от 0,1 до 10 перекрывает, по-видимому, с запасом, вероят­ные значення этого коэффициента.

На рис. 89 приведены не только упомянутые выше кри­вые ф=ф (Р; Ь), по и ограничивающие их линии 0. Действительно, наличие максимума As еще вовсе не озна­чает, что сама величина А£ при этом положительна, в то же время ясно, что возбужденно колебательпой системы воз­можно только при Л*2>0. Поэтому линии Л2=0,отде­ляющие области значений (р, ср, 6), соответствующие А^> 0,

Пых из условии Л=Л„

От областей, для которыхМ£ < 0, представляют несомпеп — ный пптерес. На рис. 89 нанесены лишь те участки кривых ф = ф (Р, Й),’соответствующих ^s — ^max, для кото­рых A-z > 0.

Рассмотрение крпвых, приведенных на рис. 89, по­зволяет сделать следующие выводы. Прежде всего видно, что, еслп не считать небольшого участка, соответствую­щего малым £», при р, песколько превышающем я, то диаграмма охватывает всю область, отвечающую усло­вию самовозбуждения системы Л2 > 0. Прп этом легко сообразить, что полученные кривые полностью соответ­ствуют диаграммам граппц устойчивости, примеры кото­рых приводились в гл. IV (см., например, рпс. 27). Изме­нение р от 0 до зх означает, что вектор Y находится в первой и четвертой четвертях, т. е. именно в тех, в кото­рых лежат основные области неустойчивостп.

Главпой особенностью кривых, соответствующих ре­жимам Л max п прпведеппых па рис. 89, является сле­дующее. Если исключить сравнительно узкие области, близкие к р=0 и р = я (онп представляют ограниченный интерес хотя бы потому, что соответствуют малым Ay, поскольку прилегают к лнния. м Лх=0), то для всех р п Ь паблюдается стремление кривых приблизиться к пря­мой ф ‘ образом, в первом приближении можпо

Говорпть, что вне зависимости от величины запаздывания в зоне горения (Р) и количественной зависимости возму­щений скорости распространения пламени от возмущепня скорости течения (6), колебательная система будет стре­миться возбудить такую гармоппку, которой соответст — я

Вует ф = т.

Значению = соответствуют амплитуды колебаний pL и vv удовлетворяющие, как это видно из (45,7), усло­вию Pi=vv Это означает, что сечение 2 должпо лежать приблизительно по середине между узламп давления п скорости.

Физический смысл полученного результата достаточно ясен. Выше уже было показано, что прп полной незави­симости Y от амплитуд п фаз колебаний газа в сечении перед 2, оптпмальное значенпе ф, которое «выберет» коле­бательпая система, будет <р=0. Этому соответствует узел скорости іл,=0, или, что то же самое, пучность давления. s Еслп предположить, что отличие Г" от нуля связано с су­ществованием перавиого пулю возмущения скорости 0 (|17! = то сразу становится ясным, что прежний ре­зультат в рассматриваемом случае становится неприме­нимым. Здесь будет происходить борьба двух тенденций. С одной стороны, будет действовать только что упоминав­шаяся тенденция приблизить плоскость теплонодвода 2 к пучности давлеппя, а с другой стороны, появится повая тепдепция сместить 2 к пучности скорости, чтобы увели — чнть (при заданном Ь) амплитуду Т. Как показывает расчет, это приводит плоскость 2 приблизительно на се­редину между указанными пучностями (или, что то же самое, узлами). С точки зрония этого рассуждения вполне закономерно н распределение кривых, соответствующих разным Ь, на рпс. 89. Чем больше Ь, тем ниже идут кри­вые, т. е. тем ближе плоскость 2 к пучности давления (ф=0), так как с увеличением Ь те же значения Y можно получить прп меньших но абсолютной величине возмуще­ниях скорости и j.

Совершенно аналогично поддается рассмотрению и тот случай, когда амплитуда 1′ зависит не от v}, а отpv Это может иметь место, например, при подаче топлива мало — напорными устройствами, которые изменяют количество вводимого в зону горения топлива в зависимости от про­тиводавления окружающей среды. Не конкретизируя рассматриваемого процесса, положим, что |1r = bpi, а запаздывание характеризуется углом а (рис. о8). Тогда режим, соответствующий максимуму положительных зна­чений As, определится следующими условиями:

TOC o "1-3" h z. у rt4bsiaa v

» ™ ~~ «j — нг—а3Ь cos ‘

(a. i — — a3b cos a — f/5Z>3} cos2cp — а±Ь. sin asin2cp<0, /(45.14) Az> 0. I

Анализ условий (45.14), аналогичных соответствую­щим условиям, рассмотренным песколько выше, тоже целесообразно провести па основании численных расчетов. Для того же примера (ЛД —0,1; Л/3=0,25) получающиеся соотношения настолько просты, что но представляется необходимым построение графиков, подобных тем, кото­рые прпведепьт на рис. 89. Вне зависимости от того, пола­гается ли Y— и0ГСф или л практически, впе зави­симости от а, числитель первого из соотношений (45.14) оказывается по абсолютной величине много меньше зна­менателя, а с учетом второго соотношения (45.14) угол ср оказывается близким к нулю. Это указывает на то, что колебательная система стремится в таких случаях возбудить гармоники, при которых плоскость теплопод­вода будет находиться в пучности давления.

Таким образом, если существенный параметр Y, ха­рактеризующий горение, возмущается колебапиямп ско­рости, то плоскость 2 как бы стремится оказаться между пучностями скорости и давления, еслп же он возмущается давлением, то плоскость 2 как бы стремится оказаться в пучности давления. Этп общие результаты довольно хорошо прослеживаются при сопоставлении эксперимен­тально полученных эшор стоячих волн давления с поло­жением области теплоподвода относительно этих эпюр.

§ 46. Экспериментальная проверка гипотезы о максимуме акустической эпергии

Хотя полученные в предьідущелі параграфе следствии пз гипотезы о максимуме акустической эпергии, излучае­мой областью теплоподвода, и могут быть подтверждены рядом качественных наблюденпй, желательно более чет­кое подтверждение этого предположения.

С целыо подобного рода экспериментальной проверки можно, например, задержав процесс вибрационного го­рения на второй стаднп (поскольку колебаппя с ограни­ченными амплитудами легче подвергнуть эксперимен­тальному исследованию), зарегистрировать амплитуды и фазы колебаний и сравнить их с теми, которые пред­сказываются высказанной гипотезой.

Если провести эксперимент по предложенной здесь схеме, то даже положительный результат не даст, конечно, полного подтверждения высказанной выше гипотезы. Это следует уже из того, что, как указывалось в § 45, гипотеза о максимуме акустической эпергии указывает на отбор механизмов возбуждения по признаку 4s=4max в про­цессе разгона колебаний. В то же время эксперимент, поставленный по предложеппой схеме, даст все соотно­шения для процесса установившихся колебаний. Поэтому оказывается необходимым принять дополнптельное пред­положение, что и в установившихся колебаниях, когда поток акустической энергии определяется потерями, со­храняет свое доминирующее значение механизм, отвечаю­щий условию Л2 = ^шах — Прп установившихся колебапиях это будет означать стремление колебательной системы реализовать в копкретпых условиях опыта процесс, даю­щий максимальные амплитуды колебаний.

Почти очевидно, что, измерив и эксперименте ампли­туды колебаний скорости, давлення и, если это необхо­димо, других параметров, невозможно утверждать, что они являются наибольшими из всех возможных в конкрет­ных условиях опыта. Поэтому проверку гипотезы можпо, по-впдпмому, провести в несколько менее общей поста­новке.

Наблюдая возникшее вибрационное горение с вполне определенным механизмом обратпой связи и произведя необходимые измерения, можно затем путем теоретиче­ского расчета установить, были ли паблюдавшиеся коле­бания такими, что амплитудно-фазовые соотношения удо­влетворяли условию Aшах — Таким образом, при этой постановке задачи можно установить лишь то, насколько амплитудно-фазовые соотношения возникшего тнпа вибра­ционного горепия соответствуют гипотезе о максиму­ме Лг, но нельзя установить, «выбран» ли колебатель­ной системой сам тип вибрационного горепия (тип механизма обратной связи) в соответствии с указаппой гипотезой.

Следовательно, высказанную выше гипотезу о макси­муме А 2 применительно к предложенному эксперименту надо заменить ее следствием: в опыте реализуется такая величина и фаза возмущения существенного параметра зоны теплоподвода I", которая прп зарегистрированных в опыте возмущениях />j и і;, дает наибольшую вели­чину As.

Чтобы проверить это теоретическое предположение, были поставлены специальные опыты. Опытная установка представляла собою трубу общей длиною 8 м с диаметром 100 мм. В эту трубу подавался зарапее подогретый воздух, в котором было предварительно испарено необходимое количество беизииа. Горение происходило ири относи­тельно малых длинах камеры сгорания, ее протяжен­ность имела порядок 800—900 мм. Пламя удерживалось стабилизатором, имевшим форму уголкового элемента, иоставлеииого вершиноп навстречу потоку.

Как впдпо из этого краткого описання, в установке такого рода не могли проявиться механизмы обратпой связи, обязанные своим существованием смесеобразова­нию. Надо было ожидать, что главным будет механизм обратной связи, обусловленный периодическим впхре — образованием за стабилизатором, а следовательно, суще­ственным параметром зоиы теплоподвода, возмущения ко­торого акустическими колебаниями замыкают обратную связь, будет эффективная скорость распространения пла­мени Uv

Чтобы убедиться в этом, Степки камеры сгорапня были выполнены из кварцевого стекла, и скоростная киносъем­ка процесса вибрационного горенпя дала типичные картипы периодического мощного вихреобразовапия за стабилизатором. Подкрашенное пламя, которое регистри­ровалось киносъемкой, позволяло записывать интеграль­ную светимость ближайшей окрестности стабилизатора па шлейфовый осциллограф, па который одновременно записывались и колебапия дпвлеппя. Полученные осцил­лограммы показали, что колебания светимости имели частоту, совпадающую с частотой колебаний давления. Скоростная кипосъемка убедила в тої/, что упомяпутые колебания светимости связаны с изменением объема, за­нятого горящими (светящимися) газами, которое, как из­вестно пз гл. IV, может быть сведепо к изменению эффек­тивной скорости распространения пламени Uv

Для вычисления Az по данным опыта следовало преж­де всего пайтн фазу и амплитуду Y=UX и других величин, необходимых для расчета величины потока акустической энергии.

Как видпо из уравнепий (45.1) условия, связывающие колебания слева и справа от зоны теплоподвода, содер­жат шесть коэффициентов н пять переменных. Все шесть коэффициентов находятся, в конечном итоге, если задапы

И М2. Первая из этих величин легко измеряется непо­средственно, а вторая столь же легко определяется, как только произведено измерение температуры газов за зоной теплоподвода. Таким образом, пахождеппе коэффициен — тив Дц, «12, . .., «2з П0 данным опыта труда не представ­ляет. Измереппе колебании давления непосредственно перед зоной гореппя и сразу за пен (рх п р.2) также не пред­ставляет технических трудностей. Из остальных трех ве­личин — у,, v2 и Y=U1 — ліннь первая поддается изме­рению при помощи термоанемометра. Но коль скоро из­мерены рх, рг и vv две другие величины, z>2 и £/",, могут быть вычислены, поскольку в спстеме двух равенств (45.1) останутся лишь дна неизвестных. Вычисление проще всего произвести затем по формуле (19.7)

= y {nmptV^PjVi).

Таким образом, замер соответствующих величин дает возможность пайти поток энергии А2, наблюдавшийся и опыте. Чтобы решить вопрос о том, подчиняется лп этот ПОТОК энергии Аъ условию Az=Am! yz, можпо произвести следующие дополнительные расчеты. Поскольку в про­цессе определения экспериментального значения Л*; най­дена п экспериментальная величина U,, можно проанали­зировать, как стало бы пзмепяться Л а, еслп бы Ux харак­теризовалось другими амплитудами п фазами нри тех же самых рх и vx. При этом вариации £/, следует произвести в окрестности значеппя Uv найдеттпого из обработки опыт — пых данных.

Результаты соответствующих расчетов приведены па рпс. 90 н 91. На этих графиках дано изменение Av для разных, наблюдавшихся в опыте, частот, в зависимо­сти от величин II пли (3 (амплптуды и фазы ^озхтущригтя скорости распространения нламепи относительно степок трубы iVT). Велнчипа # = Z7, однозначно определяет (прн заданном значении возмущение скорости распро­странения пламени Ux. Приведенная выше связь между jV п Ux показывает, что для целой, поставленных в пасто- ящем^параграфе, переход от И1 к N ничего не меняет: надо будет убедиться в том, соответствует ли эксперимен­тально зарегистрированному_режиму равенство AS=A тах, т. е. лежат ли Л2 для IV, отличных от тех, которые
вычислены пи опытным даниьш, ниже Л2, зарегистрирован­ного в опыте.

Шгещ Ж.

Er,

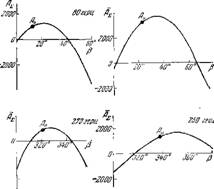
Рис. 90. Положение экспериментальных точок (А9) па кривйх AZ = AS(P).

Suffsem

Кривых панесены точки Л0, которые соответствуют опыту. Оценка точпостн эксперимента показала, что фазы реги­стрировались осциллографом с точностью ±15°, а точ­ность вычисления II, определяемая точностями замера

На рпс. 90 и 91 приведены кривые пзмепенпя в функции |N | и фазы N, обозначенной |3; на этих

ІЮгещ

-то

Pv vL и р2, имеет порядок +3 условных единицы, отло­женных но осям абсцпсс на рис. 91.

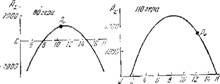
Если учесть точность определения {S и Н в опытах, то можно говорить о том, что для всех наблюдавшихся частот,

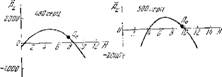
Рис. 91. Положенно эксперимента л иных точек (Л0) на кривих

Фактически реализованных колобательиой системой, режимы впбрациоипого горении лежат в окрестности ма­ксимумов кривых Зг=1з|(Р) и ~Аъ="А£(Н), что следует рассматривать как подтверждение одпого пз следствий
из гипотезы о стремлении колебательной системы реали­зовать режим, соответствующий максимуму акустической энергии, излучаемой областью теплоподвода.

Чтобы оценить степепь достоверности изображенных на рпс. 90 н 91 диаграмм, приведем пекоторьте допол­нительные данные. Кривые на этих диаграммах строились следующим образом. По замерам в опыте рх, vx и р2 прп иомощн равенств тппа (45.1) находились v2, Y=N и по­ток энергии Ал. Затем производилась вариация амплптуды N (обозначенной II) и фазы N (обозначенной (5) прп неиз­менных p. j, и для этпх измененных N вновь отыски­вался поток эпергяи As, который, как уже говорилось, оказывался меньшим, чем для фактически реализован­ного режима. Следовательно, существенный параметр, характеризующий зону горения У, оказывался всякий раз реализованным таким образом, что все другие значе — ішя У (при тех же рх, у,) давали меньшее зпачевие Совершенно ясно, что па результаты этих вычислений могли новлпять как точность измерений рх, vx и р2, так н точность определения коэффициентов аи, а1й, в равенствах (45.1). Что касается первого источника оши­бок, то с наименьшей точностью производилось измере­ние измерения р1 и р2 производились практически совершенно точно. Коэффициенты равенств (45.1) можпо было определить по формулам гл. IV, зная Мх н Мг п предполагая, что в зоне горепия происходят колебания плоского фронта пламени, за которым температура мгпо — веігпо достигает расчетного значення. Можпо было, с дру­гой стороны, уточнить как конфигурацию пламепи в зоне горения (по данным киносъемки), так н учесть постепен­ность нарастания температуры в факеле. Этот подход давал, конечно, несколько иные численные зааченпя а11» а12» а23> чем более простой, упомянутый выше.

Численный анализ показал, что хотя ошибка в измере­нии vx н возможные отличия в коэффициентах равепств (45.1) в сальной степени влияют на вычисленную величину Л2> это не может изменить сделанных выводов. Хотя чис­ленные лпачеиин. lv п изменялись, кривые Лх—Av{Ii) и = ((J) сохраняли своп вид и, главное, точки Ли практически пе смещались па этих кривых относительно их максимумов. Следовательно, вывод о стремлепип коло — бательпой системы реализовать режим Ay = Лшах пе пзме — пплся бы при более тщательпых измерениях и более точ­ной обработке опытных данных.

Относительно описанных расчетов следует сделать еще одно замечание. Как видно из методики построения кри­вых на рис. 90 и 91, при вариации Y=N не налага­лось требование выполнения краевого условия па выход­ном конце трубы. Приведенные расчеты надо рассматри­вать как выявление тенденции, а по как точные вычи­сления.

Рассмотренные здесь опыты следует расценивать в ка­чество экспериментальной иллюстрации гипотезы о мак­симуме А^, их объем явпо недостаточен для того, чтобы можно было с полной уверенностью говорить о подтвержде­нии гипотезы, Поэтому всякие новые эксиоримемтальные исследования в этом направлении представляют иесом — неииый интерес.

Надо сказать, что ряд явлении, которые наблюдаются при вибрационном горении, могут, вероятно, трактоваться с то шеи зрения стремления колебательной системы к реа­лизации режимов, характеризуемых = Дпах-

В частности, описывавшиеся в предыдущих главах скачкообразные изменения частот колебаний по мере пе­ремещения зоны горения по длине трубы можно объяснить и с точки зрения выдвинутой гипотезы. Опытные данные ие опровергают предположения, что переход с одной ча­стоты колебаний на другую связан с тем, что па повой частото количество генерирз’олюй в зоне теплоподвода акустической энергии превосходит ее количество, генери­ровавшееся па старой частоте колебаний.