Прп работе жидкостного реактивного двигателя всегда наблюдаются колебания давлення в камере сгорания, колебаппя в расходе топлива и т. п. Это приводит к колебаниям тяги, что воспринимается конструкцией, па которой установлен двигатель, как некоторая механическая вибрация. Надо сказать, что эти вибрации не представляют какой-либо опасности для конструкции, пе снижают эффективности двигателя, и их следует считать столь же естественным явлением, как и вибрации п шум автомобильного двигателя. Однако было замечено, что при известных условиях нерегулярные колебания, о которых здесь шла речь, резко изменяют свой характер. Они зиачительно увеличивают свою амплитуду, становятся строго периодическими и тем самым становятся весьма опасными для конструкции двигателя. Поэтому требования успешного развития ракетной техники привели к необходимости подробного исследования автоколебаний в каморах сгорания жидкостных рсактпвпых двигателей. Неудивительно, что в периодической литературе появился ряд статей, посвященных этой проблеме, а недавно была выпущена весьма цепная монография Крокко и Чжепа1).
Авторы указанной монографии, в полном согласии с рядом других исследователей, выступавших со своими работами в периодических изданиях, различают два вида автоколебаний в жидкостных реактивных двигателях. Одни из этих видов принято называть нпзкочастотпыми автоколебаниями, другой — высокочастотными. Разница между пимн сводится к следующему.
Низкочастотные колебания вызываются тем, что система, состоящая из камеры сгорания и топливоподающих устройств, становится неустойчивой по отношению к малым возмущениям. При этом механизм возникновения этой неустойчивости обусловлен влиянием периодических колебапий давления в камере сгорания на подачу топлива и на величину времени запаздывания воспламенения. Характерным для этого вида автоколебаний является то, что при их исследовании можно пренебрегать протяженностью камеры сгораиия, рассматривая ое как некоторый объем, во всех сечепиях которого давление изменяется одппаковым образом.
Высокочастотные колебания также вызываются тем, что система становится неустойчивой по отношению к малым возмущениям и в этом случае также определенную роль играет взаимодействие колебаний давления
в камере сгоранпя с процессом подготовки и воспламенения горючей смеси. Однако, в отличие от предыдущего случая, здесь уже нельзя пренебрегать протяженностью камеры сгорания и нельзя считать, что во всех сечениях объема камеры сгоранпя давление и другие параметры изменяются одинаковым образом.
С точки зрения механики, первый случай во многом аналогичен обычным динамическим системам (описываемым обыкновенными дифференциальными уравнениями), а второй случаи связан с распространением возмущении по сплошной среде, т. е. с явлениями акустического тина (описываемыми системами дифференциальных уравнений в частных производных). Поскольку настоящая книга посвящена изучению процессов возбуждения продольных акустических колебаний, то естественно, что здесь будет рассматриваться только задача о продольных высокочастотных колебаниях. Хотя приводимое ниже изложение вопроса несколько отлпчается от того, которое да по в монографии Крокко и Чжена (это вызвано желанием быть более близким к содержанию предыдхтцих глав), осповпые идеи п результаты заимствованы пз названной монографии. Желающим более подробно познакомиться н с пизкочастотпыми колебаниями в жидкостных реактивны^ двигателях следует порекомендовать обратиться к работе Крокко и Чжена.
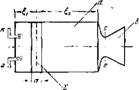
Рпс. \. Схема жидкостного рсак — тпвпого двигателя.
Прежде чем переходить к изложению вопроса, дадим краткое описание схемы жидкостного реактивного двигателя. Как известно, этот тип двигателя представляет собой цилиндрическую трубу а, с одной стороны которой устанавливается сверхзвуковое сопло б, а с другой — устройства для впрыска в камеру сгорания топлива (рис. 111). Последние включают, в частности, устройства для подачп и распыла горючего (трубопровод г на рисунке)
и окислителя (трубопровод в на рисунке). В замкнутый объем камеры сгоранпя следует, как известно, непрерывно подавать горючее (например, спирт) н окнсянтель (например, жидкий кислород). В совокупности горючее и окислитель принято называть топливом. Топливо пе всегда должно состоять из двух компонентов, как в только что рассмотренном примере. Существуют так называемые однокомнонептпьге топлива, способные к самовоспламенению при попаданпп в камеру сгорания двигателя. В этом случае вместо двух трубопроводов виг на рис. 111 сохранится лишь один. Закрытый конец камеры сгоранпя, вместе с расположенными здесь форсунками, служащими для распыла топлива, принято называть головкой, противоположный конец — соплом.
Горение в двигателе сильнейшим образом зависит от тех процессов, которые нропсходят у головки двигателя. Поскольку в камеру сгорания впрыскиваются жидкие компоненты, постольку смесеобразование играет весьма важную роль. Эффективность п быстрота сгорапия впрыснутого топлива зависят от качества распыла н смешения компонентов (если топливо не одиокомпонент — пое), от быстроты пспаренпя капелек топлива и от быстроты прогрева горючей смесп. Вся совокупность втих процессов требует для своего завершения известного времени, по прошествии которого только и может наступить интенсивная химическая реакция.
Не имея возможности дать этим процессам сколько — нибудь четкую количественную характеристику, введем в качестве некоторой суммарной характеристики время запаздывания, понимая его как время, прошедшее от момента впрыска топлива до мгновенного превращения его в продукты сгорания.
Примем для периода пндукцпн t„ соотношение (37.5), которое говорит, что период индукции связан только с давлением. В § 37 указывалось, что многие стороны фнзико-химических процессов, подвергающихся идеализации путем введения периода ипдукцпн действительно связаны с давлением. Но соотношению (37.5) можно приписать более общее значенпе. Если н другие факторы (например, относительные скорости капелек топлива и продуктов сгорания) пграют существенную роль, но их изменение закономерно связано с изменением давления, то влияние указаииых факторов можно, в конечном итоге, выразить через давлеппе. Прн переходе к безразмерным переменным соотношение (37.5) примет следующий вид:
(1 ~-рУ dt’= const. (52.1)
Воспользуемся полученной формулой для записи условий на поверхности теплоподвода (сечение потока, в котором капли топлива мгновенно превращаются в продукты сгорания).
Предположим, что количество подаваемого в камеру сгорания топлива постоянно, т. е. никак не зависит от возможных колебапий давления внутри камеры сгорания (физически это соответствует очепь большим давлениям подачи топлива).
Если секундный массовый расход топлива обозначить через т, а массу сгорающего в единицу времени топлива через wcr, то относительное возмущение массовой скорости сгорания можно определить так:
M = (52.2)
Если процесс сгорания топлива характеризуется периодом индукции тш то масса топлива, сгоревшая за время сіх, должна быть равна массе топлива, впрыснутой за время d(T— ти)
Mcv dx = md (т — ти)
Или
Mflr = m(l-^) . (52.3)
Переходя к безразмерному возмущению т, последнему равенству можно придать следующий вид:
Найдем выражение производной через известные величніш. Обратимся для этого к соотношению (52.1). Дифференцируя его по т н предполагая, что р зависит только от переменной интегрирования т’, по пе зависит от мгновенного значения тп, получим искомую величину по правилу дифференцирования интеграла с неременным верхним проделом.
Чтобы воспользоваться этим правилом, разобьем левую часть равенства (52.1) па два слагаемых:
X т
Т-ти « а
Где а —некоторая произвольная постоянная. Прн дифференцировании по т учтем, что ти является функцией т и поэтому дифференцирование второго слагаемого следует вести по правилу дифференцирования сложной функции, умножив производную от этого интеграла но выражению, взятому в качестве верхнего предела интегрирования, па производную от этого выражения по т. Итак: т
Т-ти
Поскольку равенство (52.1) имеет в правой части постоянную, полученное выражение равно пулю. Отсюда
Легко находится
Dx Ll + p(*-Tn)J
Второе слагаемое полученного равенства можно упростить, так как р < 1, а следовательно, и отклонения периода иидукцин от некоторого среднего за цикл значения ти вследствие колебания давления относительно невелики. Это позволяет написать, что
Г^їЦЛ’^і + Чр. рй)].
L 1+Р (т—т„) J
Здесь опущено обозначение зависимости р от т, а выражение р (т„) указывает лишь, что величина р берется в некоторый момент, предшествующий пастоящему на величину среднего периода нпдукцпи т1Г Таким образом,
(52.5)
Сочетание полученного равенства с найденным выражением (52.4) дает соотношение, могущее служить основой для формулирования свойств области теплоподвода:
M = r[p-p( т„)].
Найденное соотношение следует использовать прп написании уравнении, связывающих возмущенные параметры течения слева и справа от поверхности разрыва 2, являющейся, как известно, идеализированной неподвижной плоскостью теплоподвода. Чтобы написать свойства поверхности 2, используем зависимости, приведенные в гл. IV. Из сказанного выше ясно, что в уравнениях, описывающих процесс горения в жидкостных реактивных двигателях, не следует пренебрегать колебанием подачи газообразной массы в камеру сгорания, поскольку даже при постоянной подаче жидкого топлива сгорание (т. е. превращение в газ) может происходить с переменной скоростью. Пренебрегая объемом, занимаемым каплями топлива, можно считать, что моментом поступления массы в камеру сгорания является момент перехода топлива в газообразное состояние. Поэтому напишем уравнения для области горенпя о в впде (1.5.5), не пренебрегая членом ЬМ*.
(52.6)
В рассматриваемом случае в уравнениях (15.5) можно сделать следующие упрощения. Будем считать, что в установившемся процессе температура газа как слева, так и справа от области а (рпс. 111) одинакова, т. е. а1 = й,2. Это связано с тем, что и слева и справа от о пространство камеры сгорания заполпепо продуктами егорания. Кроме того, слева от а газ можно считать в средпем (в установившемся режиме) неподвижным и нзоэнтропичпым, т. е. полагать vL = 0 и б Sj = 0. Если учесть это, то, поделив первоо уравнение (15.5) на q2v2, второе
на q, o", а третье на q2o’ и учтя, что qsd2 = М*, можно получить следующую систему уравнений, записанных и "принятых я настоящей книге безразмерных переменных:
JgOs + ft-Sj^Oi + m,
2а, + ( М + + MJ-,
(52.7)
Здесь
(52.8)
М*
Сравнивая систему (52.7) с полученной ранее системой (15.7), можно видеть значительное упрощение соотношений на S для жидкостного реактивного двигателя но сравнению с соотношениями, справедливыми для горения движущихся газов. Ряд упрощений связан с тем, что г^ = 0, другие —с постоянством параметров газа в установившемся режиме для всей камеры сгорания. Последнее, в частности, приводит к тому, что ах = а2, q1^q2: 1 а ото в свою очередь дает ~ ^ q dV ^ 0 и
V
^ q (cvT — f q) dV = 0. Величину q можно положить рав — v
Ной нулю, так как вся газовая среда в камере состоит нз продуктов сгоранпя (при такой идеализации не
учитывается наличие в камере сгорания газоооразпых компонентов топлива).
Введем дальнейшее упрощающее допущение. Примем, что пространственное распределение горенпя не изменяется прп акустических колебаниях. Тогда /g = 0 и /3 = 0. Кроме того, учтем, что тепло, подводимое непосредственно в зону а, однозначно связано с подводом массы
(52.!))
Q* = qvm■
Тогда, исключая из системы (52.7) s2, можно получить свойства плоскости 2 в виде следующих двух равенств:
— , 1
Mt
(52.10)
М-
М(у. і
1 -| — . я — ггту] "-г+^тРГ-
М(х -1) 2 J 1 1 2
Если добавить к ппм соотношение (52.6), причем полагать, что входящее в пего р совпадает с [/, (это естественно, так как период индукции должен зависеть от параметров среды, через которую движутся капли топлива к области горепия о), то число переменных п системе (52.10) можно будет свести к четырем. Стоящая в правой части равенства (52.6) разпость р — р(т„) может быть выражена (ем. (4.13)) следующим образом:
F-fW = f(
Окончательно форма записи свойств поверхности S для рассматриваемого случая будет выглядеть так:
-рт„.
Mr ( і —
) Pi,
Щ + — Щ+ I
Їм
(52.11)
"(l-e-‘^Pi-
Теперь необходимо задать два краевых условия.
Одно из краевых условии получается сразу: у головки не может происходить колебаний скорости, т. е. (взяв начало отчета | на плоскости 2)
Прн £ = ^ Vj =0. (52.12)
Чтобы сформулировать второе краевое условие, обратимся к рассмотрению характера течения у выходного сонла. Если считать, что у двигателя «короткое» сопло, т. е. расстояние от сечения, соответствующего | = |2 на рис. 111 до критического сечения сопла (сечение ее) невелико по сравнению с длиной камеры сгорания ІІхІ + Іа (точнее, по сравнению с длиной стоячей волны возбужденных в камере сгорания колебаний), то в соответствии с проведенными выше для аналогичного случая рассуждениями (стр. 211)
= 0 npuЈ = ge. (52.13)
Пусть теперь £і = 0. а Ег= т — е- будем рассматривать горепие, происходящее в непосредственной близости от головки. Тогда в равенствах (52.11) можно будет принять = 0 и путем несложных преобразовании привести их к виду:
= Кз + «із» + а14/’е-е, и) pw, J,2 ^
Рго = (ааа + V + я24пГрти) р10. J
Здесь aih — некоторые постоянные, которые определяются в процессе преобразования равенств (52.11) к виду (52.14). Индексы нуль при переменных поставлены для того, чтобы подчеркнуть, что опн соответствуют 1 = 0.
Полученные соотношения почти буквально совпадают с рассматривавшимися рапее равенствами (26.4). Учтя, что краевое условие (52.13) совпадает с краевым условием, использованным в § 26, можно сразу, по аналогии с уравнением (26.5), написать следующее выражение, которое является характеристическим уравнением
рассматриваемой задачи:
(а» + а]аг + ЯипГ1*") (1 + ехр р) +
+ («и + <V + агіе-^) ( 1 — ехр ^ Р ) = 0. (52.15)
Отсюда следует:
(«12+ віаО (1 + ехр Y^p p")-H*M —аыг) С1 — охр 0
О„ ^ 1 + ехр j^j^P ) + вМ 1-ехр j-^P J
Здесь А н В — вещественная и мнимая части дроби, стоящей в средней части равенства.
Будем искать границу устойчивости. Как известно, на границе устойчивости = газ и, следовательно,
Г COS СОТи = Л (Г, СО), г sin <0ГИ = — В (г, ai),
Откуда находим
Г2 = А2(г, Ш) + В2(Г, СО). (52.18)
Задаваясь разними со, находим но уравнению (52.18) г, а затем по равенствам (52.17) ти.
Фактическое вьшолнеипе указаппых операций упрощается тем обстоят ель стволі, что, как впдно пз системы (52.11), численные коэффициенты при г и при ге~рт" отличаются лишь знаками. Поэтому и относительно коэффициентов соответствующих слагаемых равенств (52.14) можпо утверждать то же самое:
Аи — ~ аіз> а24— ~~ а23-
Но тогда равенству (52.16) (прп р = гсо) можно придать такой в’ид:
(52.17)
Г ехр (— іоот,,) = г + Ь + 1с, (52.19)
ЕД0
FlL+ai ‘ ~~ яі+дІ *
«і = («12 + «22) + («12 — «22) cos ГГ^й®’ 2
«2 = («13 + «2з) + («із — «зз) С03^Гд/2Ю.
A3=(al2-А22) sinj—j^ft),
«4 = («13 — «2з) sin со.
Переходя затем к уравнению типа (52.18), полу чим линейное относительно /• соотношение
Определив по формуле (52.20) величину г, сразу находим ти. Из сравнения мнимых и действительных частей равенства (52,19) следует:
Sin ШТи = — у, COSOJTn = 1 ■ (52.21)
Для теоретического анализа высокочастотных колебаний в жидкостных реактпвпых двигателях систему уравнений (52.7), описывающую свойства области теплоподвода, обычпо заменяют приближенной. Наппсав только первое уравнение, являющееся следствием закона сохранения потока массы, дополняют его двумя равенствами Рі — Рг и = = которые используются вместо второго и третьего уравнений (52.7).
Физически это связано с тем, что продукты сгоранпя в камере жидкостного реактивного двигателя имеют в основном одинаковую температуру по обе стороны фронта горения. Это существенно отличает процесс в двигателях рассматриваемого типа от процессов в топках и других устройствах, в которых подвод тепла к потоку холодного газа, пересекающего фронт пламени, обычно происходит без заметного увеличения массы текущего газа.
Если принять это допущение, то вместо системы (52.7) можно будет написать такую:
Ft = Pi-
Равенства (52.14) приобретают весьма простои вид:
=+м И1 — Є"е?«) -1] й„, Р 20 = Рм>
А коэффициенты уравнения (52.19) можно записать сразу в явном виде:
2
Sin jrp — О)
I>=- 1; с= 7 ^ v (52.24)
М(.1+СозТ=м5Г°0
Прежде чем идти дальше, оценим допустимость введенного здесь упрощения. С этой целыо построил; область неустойчивости для основного топа трубы по обеим методикам—точной и приближенной. Для этого возьмем следующий численный пример: х=1,2, М — 0,213, теплотворную способность топлива примем равной 2000 •
Следует заметить, что для приближенной методики зпанпе теплотворной способности топлива излишне.
Получив по формулам (52.20) и (52.21) пары значений г и ги, нанесем их на график, приведенный на рпс. 112. Крпвая 1 соответствует расчету но точной, а кривая 2—расчету по приближенной методике. Как видно из графика, обе границы устойчивости (штриховкой показана область неустойчивости) идут достаточно близко и поэтому допускаемое обычно упрощение надо считать вполне оправданным. В дальнейшем все результаты будут получаться по приближенной методике.
(52.22)
(52.23)
Если вернуться к диаграмме на рпс. 112 для того, чтобы понять основные свойства жидкостного реактивного двигателя как колебательной системы, в которой могут развиваться продольные акустические колебания, то
можно утверждать, что прн малых г (г < 0,5) самовозбу — жденне акустических колебаний вообще невозможно. Это связано с тем, что при малых г период индукции слабо зависит от давления. Наименьшим значением?•, при котором еще возможно самовозбуждение, является?-=0,5. Проще всего в этом убедиться следующим образом. Воспользовавшись равенствами (52.23), найдем выражение для потока акустической эпергии, излучаемой областью теплоподвода. Прп этом учтем, что О яо краевому условию, а температуры и давления газов по обе стороны фронта горения одинаковы. Тогда, следуя формуле (19.7), можно написать
— jpi0vi0 = M[(r-i) — r cos юти](52.25)
Поскольку рассматривается самовозбуждение системы, не имеющей потерь акустической эпергии па концах трубы, границе устойчивости будет соответствовать Л2=01 самовозбуждению > 0, а гашеншо колебапий ЛЕ<0,
Легко видеть, что стоящее в прямых скобках выражение отрицательно при малых г. Чтобы сделать его при заданпом г наибольшим, надо взять такое т,„ нри котором cos шт= —1. Тогда в прямых скобках будет 2г — 1. Указапноо выражение обращается в нуль при г = 0,5. Таким образом, наименьшим значением г, нрп котором может быть выполнено условие Аъ = 0, является г = 0,5, при г < 0,5 уі£<0, т. е. самовозбуждение невозможно.
Этот результат был получен сейчас не на основе численного примера, таким образом, утверждение, что при г < 0,5 колебательпая система не может возбудиться ни при какпх условиях, приобретает характер общей закономерности.
При >0,5 появляется область значений (г, тн), нри которых колебательная система будет возбуждаться. Интервал значений ти, допускающих самовозбуждение, увеличивается но мере роста г. Таковы общие закономерности, которые следуют пз выражения (52.25) и которые отображены на рис. 112.
Чтобы сделать эту диаграмму еще более наглядной, приведем порядок величин г и тн, наблюдавшихся в опыте,
По данным, полученным в эксперименте Крокко, Греем и Харджем[16]), величина г имеет порядок 1,3-г-1,7 (в зависимости от соотношения между количествами окислителя и горючего, поданных в камеру), а размерная величина периода ипдукцип содержится в интервале 0,15 — н 0,22 миллисекунд. Поэтому реально наблюдавшиеся значения г
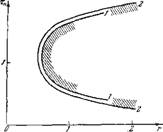
Рис. 112. Область неустойчивости, полученная точным (1) и приближенным (2) методом.
Делают возбуждение продольных акустических колебапий вполне вероятным.
Рассматриваемый тип акустических колебаний в некоторых пунктах принципиально отлпчается от научавшегося в предыдущих главах возбуждения колебаний теплоподводом и поэтому представляется целесообразным построить для него диаграмму границ устойчивости наподобие тех, которые строились в гл. Ill и IV. Наппшем равенства (52.23) в форме
По — Мр10 + Мт, ) Jho = PlQ — і
При такой записи возмущение т может зависеть не только от ри, по п от «10.
Возьмем скалярное произведение этих равенств друг на друга и учтем, что v20i>20 — 0, vl0$>10 = 0, потому что
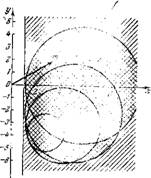
Рис. ИЗ. Диаграмма грапид устойчивости при самовозбуждении вследствие возмущения газообразования.
В системе нет потерт, акустической энергии. Тогда величины 2>]0 и ш будут связаны следующим соотношением:
Которое представлено графически на рис. 113 для |рго| = 1 в виде вертикальной прямой а;=1. Как впдпо из этой диаграммы, возбуждеппе системы стаиовнтся возможным только тогда, когда проекция безразмерного возмущения газообразования ш на ось х (иа направление plQ) ире — вышает абсолютную величину plQ. Поскольку при сделанных выше предположениях абсолютная величина т прямо пропорциональна абсолютной величине рїй
M = r(l-e~^)pv (52.26)
То условия возбуждения зависят от пх относительной величины и от фазового сдвига, т. е. в конечном итоге ет Г И Ти.
Принципиальное отличне рассматриваемого случая от изучавшихся раиее заключается в том, что вместо возмущения теплонодвода или скорости распространения пламени здесь появляется возмущение газообразования. Поскольку газообразованпе, вообще говоря, не обязательно должно быть связано с теплоподводом (горением), то этот тип возбуждения акустических колебаний мыслим в устройствах, в которых полностью исключено гореппе или теплоподвод, но в которых происходит газообразование (папрпмер, нспаренне сильно перегретой жпдкостп, которая впрыскивается в камеру с пониженным давлением), еслп, конечно, это газообразованпе будет тем пли иным образом зависеть от колебаний давления или скорости.
Надо сказать, что вместо построения приближенной границы устойчивости, изображенной на рис. 11В в виде вертикальной прямой, можно построить и точную, основываясь па уравнениях (52.10), а пе (52.22). В этом случае, как и в гл. III и IV, можііо получить семейство окружностей, центры которых движутся [в зависимости от нзмененпя взаимно связанных равенством (19.12) величин р10 и і?10] по частн дуги эллипса. Соответствующее построеппо приведено на рис. 113 для уже упоминавшегося численного примера. Все построенные окружпостп лежат справа от приближенной граппцы устойчивости и достаточно близко к пей. Таким образом, прямую 2 = 1 на диаграмме рис. 113 можно рассматривать как приближенную конфигурацию граппцы устойчивости при произвольном положении зопы горенпя вдоль осп камеры сгорапия двигателя. Прп этом расстояние между границей устойчивости и осью х равно корню пз постоянной в правой частп равенства (19.12), который совпадает с |р10| в пучности давлеппя (в построенном примере эта постоянная взята равной единице).
Из рассмотрения диаграмм устойчивости становится очевидным, что система пе может возбудиться, когда фронт горенпя будет располагаться в узле давления даже в том случае, если (например, под действием колебапий скорости) газообразование будет иметь отличную от нуля колебательную составляющую. Это видно нз того, что область неустойчивости не захватывает ни одного участка оси у, более подробный анализ показывает, что, например, нріг /?10=0; iQ = i окружность, соответствующая изображенной в правой части рпс. 28, имеет мппмый радиус.
После сделанных замечаний вернемся к обсуждению диаграммы, приведенной на рпс. 112. На этой диаграмме даны не все области неустойчивости, а лишь одна из них, соответствующая колебаниям основного топа п характеризуемая наименьшими значениями ти для этой гармоники Следует, правда, напомнить, что само понятие гармоники может прилагаться к системе, в которой свойства 2 переменны лпшь с известными оговорками (подробнее об этом см. § 27). Еслп условиться считать за собственные частоты системы те, которые получились бы при акустических колебаниях в той же камере сгорания и при том же потоке газа, но без взаимодействия с зоной горения, то они определяются формулой (5.4)
И = (1 — М2) Кл 1;2;3; .. .). (52.27)
В рассматриваемом случае такие частоты возникают при /-=0,5 и
OT„ = iVrt (iV=l, 3, 5, …). (52.28)
Проще всего убедиться в этом, используя первое равенство (52.23). Вспомнив, что па границе устойчивости (} = г£0, легко видеть, что при г = 0,5 и (отш определяемых по соотношению (52.28), и20 = 0, так как краевое условие дает v10 = 0. Следовательно, в этом случае краевые условия можно записать в виде v2 = 0 при і = 0 и У2 = 0 при £ = 1, т. е. сформулировать их для коицов трубы так, чтобы между концевыми сечоииямн пе было фронта горения (прп | = 0 краевое условие выражается теперь через v2, а пе и,). Полученная в § 5 формула
(52.27) выводилась в таком именно предположении — на концах трубы одинаковые узлы (оба давления или обе скорости), а между ними нет поверхностей разрыва. Впрочем, частоты, даваемые формулой (52.27), можно найтп п непосредственно из соотношений, полученных в настоящем параграфе. При (оти, определяемых формулой (52.28) (ее можно рассматривать как следствие равенства (52.21) для — 1 и /’ = 0,5), величина мнимой части равенства (52.19) должна быть равной нулю. Этому соответствует с = 0, или, по формуле (52.24),
2 2 sin о> = 0, что дает —= т. е. формулу
(52.27) Г л _2д,/а м = К ті не является решением для нечет
Ных к} так как в этом случае знаменатель в выражении
![]()
Для с (52.24) обращается в нуль и с— со
Следовательно, те частоты, которые обычно принято называть собственными частотами, возбуждаются лишь при вполне определенных г и ти. На рнс. 112 этому соответствует всего одна точка границы устойчивости — та, для которой г = 0,5. Легко убедиться в том, что эта точка получается нри К = і и = 1 в формулах (52.27)
И (52.28).
Для других точек, лежащих на границе устойчивости, частоты о отличаются от частот, определяемых выражением (52.27). Если оставаться в пределах значении г, показанных на рис. 112, то для крайних точек эти частоты будут отличаться от частоты, соответствующей г=0,5 на ± 10% (для верхней ветви границы устойчивости они будут мепыпе, для нижней — больше). Поскольку, как это впдно из приведенного примера, в довольпо широколі дпапазопе измепепий г возбужденные частоты близки к величинам, даваемым формулой (52.27), последним выражением можно пользоваться для приближенной оценки частот колебаний.
Изображенная иа рпс. 112 кривая не является единственной границей устойчивости в плоскости параметров (г; Ти). Действительно, если обратиться к выражению (52.19), то сразу видно, что если для него существует
хотя одно решение ТІ; ©*, то на его основе можно построить бесчисленное множество решений следующими двумя путями.
![]()
Во-первых, не пзменяя г и ничего не меняя в правой части равенства (в том числе и со*), можно сразу утверждать, что если решение существует для некоторого та, то оно будет существовать и для всех
= + fJV = 1. 2, З, …). (52.29)
Во-вторых, можно поступить следующим образом. Полагая N = const н сохраняй изменим аргументы входящих в коэффициенты b и с тригонометрических функций следующим образом:
![]()
1 — ЛЯ
2(АГ-1)я [К=і, 2, 3, . . .).
Здесь, как п в предыдущем случае, со* — частота, соответствующая /£ = 1 (первой гармонике), а со — частоты для всех гармоник.
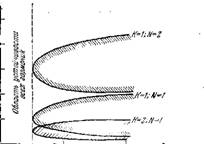
Приведенное здесь рассуждение можно приложить к каждой точке границы устойчивости, изображенной па рис. 112. Следовательно, всю границу можно перестроить и получить бесчисленное множество областей пеустойчпвости для всех комбинаций К н N.
Соответствующее построеппе для нескольких комбинаций значений К и N приведено на рнс. 114. Как видпо пз приведенной диаграммы, увелпченпе К опускает область неустойчивости, в то время как увеличение N поднимает ее. Если взять все возможные комбинации значений К и N, то практически вся область, лежащая справа от штриховой лпнип г=0,5, будет заполнена областями неустойчивости. Следовательно, прн?• > 0,5 и при любом ти (кроме, конечно. ти =0) колебательная система способна к возбуждению. В зависимости от ти н г это будет касаться той пли иной гармоники пли сразу нескольких гармоник.
До сих пор рассматривался почти исключительно тот случай, когда фронт горения расположен в непосредственной блпзостп от головки двигателя. Единственным исключением было построение диаграммы устойчивости на рис. ИЗ, которая остается справедливой для произвольного расположения фронта горения по длипе камеры сгорания.
При обсуждении указанной диаграммы говорилось, в частности, что в узле давления возбуждение системы
3
Г
Невозможно. По это лгу следует проанализировать более подробно вопрос о склонности рассматриваемой колебательной системы к самовозбуждению в завис им ости от положения фронта горенпя по длине камеры сгорания двигателя.
7
‘ 7 1 Т
Рис. 1М. Области неустойчивости для двух гар — мопик системы.
Чтобы осуществить такой анализ, следует пользоваться точными соотношениями для фронта горения (52.11), а не приближенными (52.22). Это связано с тем, что по мере перемещения к узлу давления (т. е. по мере уменьшения абсолютных величин рг и рг и увеличения vx и уй) пренебрежение членом, имеющим множителем У2 во втором |іаіірнстве_(52.7), является незаконным. Действительно.
Условие которое заменяет второе уравнение (52.7)
В соотношениях (52.22) (в них, кроме того, полагается s, = s2—0), можпо рассматривать как приближенную запись второго равенства (52.7) при s2=0, поскольку > 1. Однако при 0 и 0 такое утверждение становится ошибочным1).
Выше было показано, что возбуждение продольных акустических колебаний в жидкостных реактивных двигателях существенно связано с двумя параметрами: г и ти. Приступая к анализу влияния на самовозбуждение колебаний относительного расстояния фропта горения от головки двигателя надо условиться о предположениях, которые будут сделаны относительно г н ти. Величина г будот задаваться и оставаться постоянной. Параметр ти будем считать переменным и выбирать его так, чтобы cos соти = —1. Если выбирать т„ пз написанного условия, то будут обеспечиваться наилучшие условия для возбуждения колебаний. Это видно, например, из того, что при cos о)Ти = —1 вектор т па диаграмме рис. 113 располагается горизонтально (фазы тир будут совпадать) и поэтому возбуждение системы окажется воз-
*) В этом пункте в упоминавшейся книге Крокко п Чжена (а также в статьях названных авторов в церподической литературе) допускается неточность. Они пользуются приближенным соотношением тина (52.22) для произвольного положення фропта горе — пня н делают ряд упрощающих предположений, законность которых пе вполпе ясна. В результате полученные ими границы устойчивости {фиг. 29 названной книги л ряд другнх) вызывают сомнение. Это видно, в частности, из такого примера. Рассмотрим устойчивость основного топа при положешш фронта горепия В середине камеры сгоранпя, т. е. в узле давления. Если пользоваться соотношением тпца (52.22), то это даст рі^рч— 0 n f1=&2. или (учитывая, что п= 1 и т=) 6Я=0 и 6А’=0 (см. формулы (17.1)}. Тогда в системе без потерь тина рассматриваемой в настоящем параграфе будут нейтральные колебания. Это подробно показано в § 22 при обсуждении равенства (22.6). Следовательно, при положении фронта горения в середяие камеры сгорания система будет на границе устойчивости. В книге же Крокко и Чжена такому положению фронта горения соответствует устойчивость. Надо заметить, что возможные уточнения могут изменить лшпь количественную, но не качественную сторопу выводов Крокко п Чжепа.
Можным прп минимальной абсолютной величине т. Если указанное условие выполнено, а /’=0,5, то частоты колебаний даются формулой (52.27), т. е. совпадают с «естественными» акустпческпмп частотами. Поскольку ниже будут рассматриваться сравнительно близкие к 0,5 значения то и частоты колебаний должны быть близкими к частотам (52.27).
Таким образом, ниже будут рассмотрены колебания с частотами, близкими к обычным акустическим частотам, и при таких ти, которые в известной мере наибольшим образом содействуют возникновению автоколебаний.
Пусть г > 0,5. Тогда при положении фронта горения у головки колебательная система будет возбуждаться (это видно из рис. 114). Начнем перемещать фронт гореппя от головки и найдем положение, при котором само- возбуждеппе станет невозможным. Напишем выражение для потока акустической энергии, излучаемой зоной горения, и приравняем его нулю. При сделанных предположениях он будет равен
= у (Рго^ао -Wio) = у («іЙо + аА) = 0- (52.31)
Где ах и а2 — численные коэффициенты, которые легко получаются _ при почленном скалярном перемножении равенств (52.11), приведенных к впду (52.14), друг на друга с учетом того, что при Рти = гсотп, взятых по оговоренному выше условию, 1 —^Ти = 2.
Величины и v� связапы равенством (45.6) и поэтому абсолютные величины р10 и v10 могут быть записаны прп помощи формул (45.7). Тогда равенство (52.31) сведется к следующему уравпению относительно параметра ф, определяющего положение сечения X вдоль стоячей волны акустических колебаний:
Ах cos2 ф + а. г sin’- ф = 0
Или Откуда ^ „
Sin ф= j/ (52.32)
Построим для упоминающегося выше численного примера зависимость ср от г (коэффициент (i} является функцией /•). Резз’льтаты расчетов можпо представить следующей таблицей:
|
0,50 |
0,75 |
1,25 |
11,00 |
|
|
<е | |
0 Л 0 —я |
0,35 2,79 —0,35 —2,79 |
0,59 2,55 —0,59 —2,53 |
0,71 2,43 -0,71 —2,43 |
Чтобы придать этому расчету наглядность, яа рис. 115 изображена эпюра стоячей волны давления и скорости

Рис. 115. Эпюры стоячих волп давления и скорости в области неустойчивости для различных г.
При изменении ф от 0 до ли положення найденных сечений на ней. Как видно из диаграммы, по мере увеличе — ни я г увеличиваются области неустойчивости в окрестностях ф=0 и ф = л;. Это означает для первой гармоники, что иеустойчивость будет возникать в двух случаях: при положении фронта гореипя у головки и прп положении его у сопла. Пользуясь найденными величппамн,
1-М*"
Зл —
2л
?л
! 1 I I I
О 0.2 0.4 ч 0,5 0,8 1,0 4
Рис. Пв. Диаграмма распределения областей неустойчивости: для первых четырех гармоник, в зависимости от положения плоскости горения по длине камеры сгорания.
Можпо построить диаграмму распределения зоп устойчивого и неустойчивого процесса, в зависимости от положения фронта горения по длине трубы, паподобпе диаграмм рис. 48. Поскольку слева и справа от зопы горения температура газов одинакова, частота гармоники не будет изменяться при смещении плоскости горення вдоль камеры двигателя. На каждой стоячей волне можно отметить точки, соответствующие приведенным в таблице значениям параметра ф. В таком случае, отмечая, как и в предыдущих главах, области неустойчивости прямыми липнями, легко построить диаграмму, приведенную на рис. 116, для какого-либо зафиксированного значения г.
Из диаграммы на рис. 116 видно, что если процесс в камере сгорания склонен к вибрационному горению, то оно должно наступить вне зависимости от положения зоны горенпя по длине камеры сгорания. Разпида будет заключаться лишь в том, что в зависимости от координаты фропта горения 0 < < 1 будет возбуждаться та или иная гармоника.
Чтобы ввести дополнительную ясность в этот вопрос, напомним, что в па сто ищем параграфе рассматривается система без потерь. Еслп написать краевое условие у сопла более строго, с учетолі градиента скорости в нем, то, как показано в книге Крокко и Чжепа, демпфирующее влияние сонла будет возрастать с увеличением частоты колебаний. Поэтому возбуждение высших гармоник становится маловероятным, что характерно и для вибрационного горения газовых горючих смесей в трубах (см. гл. VI).
Приведенная па рис. 116 диаграмма напоминает аналогичные диаграммы рнс. 48, 49 и др. В обоих случаях рассматривается изменение номера возбуждаемой гармоники в зависимости от положения зоны горения по длине трубы. В конце гл. V рассматривалась и обратная задача: прп неизменных свойствах зоны горения и неизменной длине горячей части проследить влияние изменения общей длины трубы на характер колебаний. Там было показано, что общее удлинение трубы при сохранении горячей части ведет к тому, что система переходит к более высоким гармоникам, приблизительно сохраняя неизменной размерную частоту колебаппй.
Аналогичное заключение должно быть справедливым п для жидкостных реактивных двигателей. Это явление фактически наблюдалось Крокко, Греем и Харджем1). Постепенно удлиняя камеру сгорания, онп зарегистрировали переход колебаний с основного топа па вторую гармонику, а со второй на третью, что полностью согласуется с развитой в конце гл. V точкой зренпя.
В настоящем параграфе было дапо лишь элементарное изложение теории высокочастотных продольных акустических колебаний в жидкостных реактивных двигателях. Интересующимся более полным изложением вопроса следует порекомендовать обратиться к уже упоминавшейся
J) с г о с с о L., fir еу J., Н а г г і j е D. Т., Jet Propulsion, 1958. № 12.
Монографии Крокко и Чжена и к соответствующим статьям в периодической литературе.
В заключение настоящего параграфа сделаем одно замечание. Во всех предыдущих разделах многократно подчеркивалось, что в конечном итоге причиной возбуждения вибрационного гореппя является возмущение теплоподвода пли эффективной скорости распространения пламени. В — случае возбуждения акустических колебаний в жидкостных реактивных двигателях основным является возмущение газообразования (возмущение расхода некоторого источника массы, расположенного в зопе горения). Следовательно, вибрационное горение может иметь самую различную природу. В общем случае оно может возбуждаться за счет любого слагаемого, входящего в систему (15.5) и описывающего процесс внутри области а. Это может быть ЬМ* (рассмотренный только что случай), бQ* (труба Рийке), подвижность фропта пла — менп, т. е. отличие от нуля входящих во все три уравнения частных производных от интегралов по объему V (случай, рассмотренный в § 49), возмущение теплотворной способности смеси би полноты сгораппя bqx—bqz (пример, приведенный в § 25). Наконец, возбужденпе акустических колебаний может оказаться связанным с отличием от нуля слагаемого ЬРХ. Этот процесс реализуется, например, в тех случаях, когда в зопе а происходит периодический срыв вихрей (без горения). Тогда взаимодействие впхреобразования с акустическими колебаниями может привести к самовозбуждению колебательной системы. Поскольку этот случай никак не связан с процессом горенпя, оп в книге не рассматривался.
Такое разнообразие прпчпп возбуждения продольных акустических колебаний требует самого внимательного анализа всех входящих в систему (15.5) переменных до того, как будет принята схема идеализации процесса возмущенного горенпя.
Coward Н. F., Harfcwell F. J., Georgson Е. Н. М., опт. ої the Chexuicai Socioty, 1482, 1937.
[2] Мог к ТТ. J., Analysis of heat-driven oscillations of gas flows, Appl. Sncni. Ros., 1957, A6, № 4.
Термин механизм понимается здесь и шоке восьма широко. Это обычно ряд физических процессов, объединенных причшшой
СВЯЗЬЮ.
[4]) Настоящей параграф несколько выходит из общего плана главы. Ой помещен здесь, так как задача решается в вем эперге — тичесшш методом.
[5] Здесь и лижр индекс/л «единица» у р, v и о) опускаются.
12*
[6] Индекс «единица» у w далее опускается.
[7]) Напомним еще раз, что при [ v I со решение имеет лишь формальний смысл. Чтобы получить пстивнуто картину повеления системы при параметрах, дающих | v | -> со, следовало бы решить задачу с учетом начальных условий и нелинейных свойств сястсмы.
*) Л. Д. Л а н д а у и Е. М. Л и ф ш и ц, Механика сплошных сред, Гостехиздат, 1953.
[9]) Это ограничение может быть легко снято.
Ческой записью сделапного в самом начале предположения, что на стацпопарный плоский фропт пламепп наложено периодическое по времени н по коордпнате у возмущение.
Подставив значения переменпых, записанных в виде равенств (38.9), (38.10) и (38.11), д»яі = 0в условия, связывающие решения для холодного п горячего газов
[11]) См. экспериментальные графики рис. 50. Более подробное изложение этого явления будет дано в следующей главе.
) LoJm 010 условие TU. выполняется, то формула (48.10) становити несколько сложнее II лето получается пз (48.3) в (48 4). Оиычио уеловля (48.Я) выполняются.
[13]) Идельчнк U. К., Справочник до гидравлическому сопротивлению фасонных и прямых частей трубопроводов. Издание
Центрального аэрогидродинамического института им. Н. Е. Жуковского, 1У50.
[15] N і с h о 1 s о n Н. М., Й a d с 1 і f f е A., Pressure fluctuations in a jet engine. Brit. Journ. Appl. Phys., v. 4, N 12, 1953.
J) Luigi С г о с с о and Sin-J Cheng, Theory oЈ Combustion Instability in Liquid Propellant Rocket Motors. Butlerworth scientific publications, 1956. Русский перевод: Лупдяш Крокко и Ч ж е н С п п ь-и, Теория неустойчивости горешш в жидкостных реактивных двигателях, Изд-во ипостр. литературы, Москва. 1958,
[16] С г о с с о L., Grey J., Н а г г і і е D. Т., Jet Propulsion, 1958, № 12.
32 В. В. Раушепбах



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике