Процесс превращения тепловой энергии тела в лучистую называется тепловым излучением.
Тепловое состояние тела характеризуется его температурой.
Любое тело, имеющее температуру выше абсолютного нуля, непрерывно излучает лучистую энергию. В зависимости от температуры и состояния поверхности оно испускает то или иное излучение. Большая часть этого излучения при температурах, которые мы умеем получать, лежит в инфракрасной области.
Так, например, если принять всю энергию, излучаемую вакуумной лампой при температуре вольфрамовой нити 7 = 2500° К, за 100%, то только 7—12% лучистой энергии приходится на энергетическое излучение в видимой части спектра, а остальная часть энергии, за исключением небольших потерь в держателях нити накаливания, излучается в пространство в виде инфракрасных лучей.
Если температура объекта превышает 825° К, спектр излучаемой энергии содержит лучи, видимые невооруженным глазом. Изменение цвета объекта обусловливается его тепловым излучением в зависимости от температуры (табл. 1).
|
Таблица 1 Цвет объекта в зависимости от его температуры
|
Результаты простого наблюдения указывают на близкое родство тепловых лучей и лучей видимого света. Вместе с тем мы знаем, что при температуре ниже 825° К излучения становятся невидимыми.
Качественные особенности теплового излучения определяются различием в длинах волн, зависящих от температуры излучателей. При встречающихся в теплотехнической практике температурах передача тепла излучением происходит в ближней инфракрасной области спектра, простирающейся на длины волн от 0,77 до 3 мк, а в средней области спектра с длинами волн 3— 10 мк. Излучение в видимой области спектра с длинами волн 0,4—0,77 мк значительно заметно только в электрических излучателях с очень высокими температурами нити накала.
Излучение, испускаемое телом, называют монохроматическим, если оно соответствует узкому интервалу длин волны от Л, до Я + и интегральным (полным), если оно соответствует интегралу длин волн от Л = 0 до Я = оо.
Если лучистый поток падает на поверхность тела, то одна часть потока отражается (зеркально или диффузно), другая проходит сквозь тело и в зависимости от его коэффициента преломления изменяет свое направление, а третья часть целиком поглощается телом.
Отражательная способность тела (коэффициент отражения) характеризуется отношением отраженной телом лучистой энергии £отр к падающей энергии Епад:
J. Ертр
Епад
Пропускательная способность тела (коэффициент пропускания) характеризуется отношением пропущенной телом лучистой энергии к падающей энергии:
D = £проп . £пад
Поглощательная способность тела (коэффициент поглощения) характеризуется отношением поглощенной телом лучистой энергии Епогл к падающей энергии £пад:
Д _ -^погл
•Спад
Из сказанного следует, что между а, г и D существует зависимость, т. е.
A + r. + d= 1.
|
9 |
Отражение падающего потока может быть зеркальным (угол падения равен углу отражения) или диффузным (рассеяйным). Зеркальное отражение дают полированные поверхности, причем величина коэффициента отражения г зависит от степени полировки поверхности. Коэффициенты пропускания и поглощения зависят от химического строения и структуры вещества, а также от толщины слоя облучаемого вещества. Для жидких и газообразных веществ величина этих коэффициентов характе-
2—882
Ризуется размерами и количеством отдельных частиц составляющих эти вещества. Если
А = 1 и R. = d = 0,
То вся лучистая энергия, падающая на тело, поглощается им. Такое тело принято называть абсолютно черным. Если
Г — 1 и а = d = О,
То вся лучистая энергия, падающая на тело, отражается им. Такое тело принято называть абсолютно белым.
Если
D = 1, то а = г — 0.
В этом случае лучистая энергия, падающая на тело, проходит через него. Такое тело называется абсолютно прозрачным (диатермичным). t
В природе нет абсолютно черных, белых и прозрачных тел. Поэтому соотношения между а, г и D зависят от вида тел, характера их поверхности и температуры (наши обычные оценки цвета поверхности неприменимы к инфракрасному излучению; большинство поверхностей по коэффициенту поглощения может быть отнесено к разряду «черных»). Все твердые тела и жидкости (в слое толщиной в несколько мм) для области инфракрасного излучения практически не прозрачна Для них и a + r= 1. Газы; за исключением углекислоты и водяных паров, для этой области спектра диатермичны.
Следовательно, если данное тело хорошо отражает лучистую энергию, то это же тело плохо поглощает ее и наоборот. Однако существуют телэ, которые в определенном диапазоне волн и при определенной толщине их слоя являются прозрачными для лучистой энергий.
‘Например, кварц при толщине до 1 мм прозрачен для свето — ■ вых, ультрафиолетовых и инфракрасных лучей, но при толщине в несколько мм он уже становится непрозрачным для инфракрасных. Оконное стекло прозрачно для световых лучей (опять — таки до определенной толщины), но непрозрачно для ультрафиолетовых и инфракрасных с длиной волны Я более 5 мк. Каменная соль прозрачна для инфракрасных лучей и непрозрачна для ультрафиолетовых.
Аналогичное положение наблюдается также при поглощении и отражении лучистой энергии. Белые поверхности хорошо отражают видимые световые лучи и практически поглощают инфракрасные. Для поглощения и отражения инфракрасных лучей большое значение имеет состояние поверхности тела. Отражательная способность у гладких и полированных поверхностей во много раз выше, чем у шероховатых. Наибольшей поглоща — тельной способностью обладают тела, покрытые платиновой
|
• Таблица 2 Величним а, г и D для некоторых материалов
|
Чернью или сажей. В ограниченном интервале длин волн они поглощают до 90—96%’ инфракрасного излучения.
В табл. 2 приведены величины A, Г и D для некоторых материалов при облучении световыми и близкими к ним инфракрасными лучами.
Наиболее полно свойствами абсолютно черного тела обладает отверстие в стенке полого шара, предложенное русским физиком В. А. Михельсоном.
|
Рис. 3. Принципиальная схема абсолютно черного тела |
Это тело, схема’которого показана на рис. 3, представляет собой полый шар с небольшим отверстием и зачерненной внутренней поверхностью, поглощатель — ная способность которой равна 90%. Если направить поток лучистой энергии через отверстие шара, то при падении луча на внутреннюю стенку 90% энергии поглотится, отраженный же от нее лучистый поток (10%) снова попадает на стенку и при вторичном отражении снизит свою энергию до 1% первоначальной величины, а при последующем отражении до 0,1%. Если лучистый поток выйдет из отверстия после трехкратного отражения, то суммарная поглощательная способность полого тела будет равна 0,999, т. е. очень близка к единице. ‘
|
И |
Внутренняя поверхность полого тела не только поглощает, но при нагреве его до определенной температуры излучает как абсолютно черное тело. Эти особенности отражения и поглощения лучистой энергии в полом шаре проявляются и в практиче-
2*
ских условиях инфракрасного нагрева тел. Так, например, чем глубже впадины (шероховатость) на поверхности облучаемого тела, тем выше его поглотительная способность по сравнению
С более гладкой поверхностью данного тела. Этим можно объяснить увеличение поглощательной способности тел при увеличении их шероховатости или пористости.
При расчетах, связанных с лучистым теплообменом, применяются понятия о лучистом потоке Q, энергии излучения Е и спектральной интенсивности излучения /.
Лучистым потоком называется полное количество энергии, излучаемое поверхностью тела F в единицу времени, т. е.
Q = EF ккалч,.
Эта величина характеризует полную мощность излучателя.
Энергией излучения называется количество энергии, излучаемой единицей поверхности тела в единицу времени.
|
|
Эта величина характеризует удельную мощность излучателя.
Спектральной интенсивностью излучения называется удельная энергия монохроматического излучения, характеризующая спектральную удельную мощность излучателя, т. е.
|
/ |
DE% I а
= ——————————————— ккал М2-ч- мк.
D% ‘
Излучение любого твердого тела характеризуется непрерывным спектром распределения энергии излучения по длинам волн, однако сам спектр излучения является неравномерным и различным для разных тел.
|
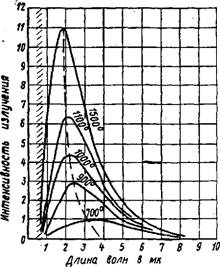
Рис. 4. Спектральное распределение интенсивности излучения абсолютно черного тела (заштрихованная часть— видимый свет) |
В основу теплотехнических расчетов при излучении положены универсальные законы излучения абсолютно черного тела, поглощающего излучения любой длины волны. Распределение интенсивности излучения абсолютно черного тела в зависимости
от его температуры и длины волны излучения показано кривыми на рис. 4. Характерными особенностями этих кривых являются: наличие разных максимумов интенсивности излучения для различных температур, резкий спад кривых в сторону коротких волн и пологий спад в сторону длинных волн. Это спра^ ведливо и для применяемых в практике излучателей (за исклкн чением газовых с пористыми излучающими насадками), интен-» сивность излучения которых показана на рис. 5.
■ 16
1 — солнце <>6000° С; 2 — инфракрасная лампа с вольфрамовой нитью /=]900°С; 3 — керамический излучатель с температурой поверхности 800° С: 4 — темный излучатель с температурой поверхности 500° С; 5 — радиаторы центрального отопления с температурой поверхности 98° С
Об особенностях спектра излучения газовых горелок инфракрасного излучения с пористыми насадками будет сказано ниже.
Закон Планка устанавливает зависимость интенсивности излучения для черного тела от длины волны Я и от абсолютной температуры Т
/х = ~ ккал1мг-ч.-мк,
Ил
Где /— лучеиспускательная способность; X — длина волны.
|
I |
Планк установил, что для абсолютно черного тела интенсивность излучения равна:
‘ і »V ‘,>’•’
Где Сі—постоянная, равная 3,22-10~16 ккал • м2/ч;
С2 — постоянная, равная 1,44-Ю-2 лі<°К.
Из выражения для /хо видно, что при % = 0 и %=оо Д0=0. Следовательно, черное тело испускает лучи с различной длиной волны при Т>0. Отсюда следует, что с повышением температуры тела интенсивность излучения увеличивается, достигая известного максимума в интервале между предельными значениями % = 0 — н оо. При малых значениях %Т последнее выражение может быть упрощено.
Графическое изображение закона Планка приведено на рис. 4, из которого видно, что каждой температуре Т отвечает своя кривая /хо, имеющая максимум тем больший, чем выше температура. С увеличением Т максимумы /хо смещены в сторону более коротких волн (Кт).
Закон смещения максимумов Ho сформулирован Вином до закона Планка. Закон Вина аналитически может быть получен, Dl
Если производную —— приравнять нулю и решить полученное DX
Уравнение относительно произведения %т Т. Таким образом, Можно получить математическое выражение этого закона.
2,9мк° К = const.
Следовательно, длина волны, при которой Ixo, Имеет максимум при заданной температуре
2 9
ГА. ~ — мк. т
Если это выражение подставить в выражение для /хо, то максимум интенсивности излучения, пропорциональный пятой степени температуры, резко возрастает с увеличением Т.
Пользуясь этим законом, легко определить длину волны, соответствующую максимуму интенсивности излучения абсолютно черного тела.
Закон Стефана — Больцмана устанавливает зависимость полной энергии излучения абсолютно черного тела от температуры. Количество энергии, излучаемой черным телом при любой длине волны при данной температуре Т, может быть найдено из выражения
^0 = Донесли это выражение проинтегрировать в пределах от Я=0 до Я=оо.
Таким образом, лучеиспускательная способность черного тела
00 QO
О о
Н
Решение этого интеграла может быть получено, если интегральную функцию —^ разложить в следующий ряд:
С 2 2 С 2 3 Cjs
Є — f — e ‘ — j — e +’ • •
Окончательное решение представится в таком виде:
Е0 = о0 Т4 Ккалімі • ч.
Чи’словое значение с0 при приведенных выше постоянных С і и С2 составляет:
С0 = 4,96-10-8 ккал/ж2-«-°К4.
Величина с0 называется коэффициентом, (или постоянной) излучения абсолютно черного тела. Так как числовое значение О0 очень мало, а Т велико, то выражению для Е0 в технических расчетах удобнее придать вид
£0 = С0 (0,017)*, где Со = 4,96 Ккалім2 • ч • °К4.
Приведенные формулы для Е0 представляют математическое выражение закона Стефана—Больцмана.
Закон Стефана — Больцмана остается справедливым и для других тел, которые, как и черные тела, имеют непрерывный спектр излучения. Такие тела, для которых соблюдается закон четвертых степеней Е = С (0,01 Т)І, называются серыми телами, а их излучение-—серым. Для таких тел отношение спектральной интенсивности излучения к интенсивности черного излучения при той же длине луча для всего интервала длины волн от 0 до оо остается постоянным, т. е.
~~ — const. ixo
Таким образом, спектр серого излучения имеет такой же характер, как и спектр черного тела. Из этого следует, что степень черноты тела при любой длине волны
Е= — = —1 = JL< і
J хо Ео С0
Для идеально серого тела при всех температурах є = const и его энергия излучения
Е = єІ;0 — ЄСд (OjOlT4)4,
Т. е. она меньше энергии излучения черного тела при той же температуре; є (степень черноты тела)—безразмерная опыт-, ная величина, которая меняется от 0 до 1; для ряда материалов значения приведены в табл. 3.
Ч ТаблицаЗ
Степень черноты Є для различных материалов
Материалы
Алюминий полированный………………………
» шероховатый……………………………………….
Железо полированное………………………………
» обработанное наждаком.
Окисленное……………………………………………
Окисленное гладкое…. литое необработанное. . . Стальное литье полированное. . . Сталь листовая шлифованная. . . Чугун обточенный ……..
Окись железа.. І………………………………………
Золото полированное……………………………..
Латунная пластина: прокатанная с естественной поверхно
Стью…………………………………………………………….
Прокатанная, обработанная грубы
Наждаком………………………………………………….
Тусклая…………………………………………….. : .
Медь, тщательно полированная, элект
Ролитная…………………………………………………….
Медь шабреная до блеска, но не зер
Кальная. . …………………………………………………..
Окись меди………………………………………………
Расплавленная медь………………………………..
Молибденовая нить………………………………….
Никель технически чистый, полированный Никелированное травленое железо непо
Лированное………………………………………………..
Никелевая проволока………………………………
Окись никеля. . ………………………………………
Хромоникель…………………………………………..
Олово, блестящее луженое листовое же
Лезо……………………………………………………………..
, Платина чистая, полированная пластина
Платиновая лента. . ………………………………..
» нить………………………………………………………..
» проволока………………………………………………
Ртуть очень чистая………………………………….
Свинец серый окисленный………………………
Серебро полированное чистое. . .
Хром……………………………………………………….
Цинк торговый (99,1%) полированный Оцинкованное листовое железо блестящее Оцинкованное листовое железо серое
Окисленное.
Асбестовый картон………………………………………
Асбестовая бумага……………………………………….
Бумага тонкая, наклеенная на металлическую пластину
Вода……………………………………………………………..
Гипс……………………………………………………………..
Дуб строганый………………………………. • " ‘ ‘
|
|
Кварц плавленый шероховатый. . .
|
50—100 |
0,04—0,06 |
|
20—50 |
0,06—0,07 |
|
400—1000 |
0,14—0,38 |
|
20 |
0,242 |
|
100 |
0,736 |
|
125—525 |
0,78—0,82 |
|
900—1100 |
0,87—0,95 |
|
770—1040 |
0,52—0,56 |
|
940—1100 • |
0,55—0,61 |
|
800—1000 |
0,6—0,7 |
|
500—1200 |
0,85—0,95 |
|
225—635 |
0,018—0,035 |
|
20 |
0,06 |
|
20 20—350 |
0,2 0,22 |
|
80—115 |
0,018—0,023 |
|
20 800—1100 1100—1300 700—2500 200—400 |
0,07 0,66—0,54 0,13—0,15 0,1 —0,3 0,07—0,09 |
|
20 200—1000 500—1250 125-1034 |
0,11—0,4 0,1 —0,2 0,52—0,86 0,64—0,76 |
|
20—50 200—600 900—1100 25—1230 225—1375 0—100 20 200—600 100—1000 200—300 30 |
0,04—0,06 0,05—0,1 0,12—0,17 0,036—0,092 0,073-0,182 0,09—0,12 , 0,28 0,02—0,03 0,08—0,26 0,04—0,05 0,23 |
|
20 20 40—400 |
0,28 , 0,96 0,93—0,95 |
|
20 0—100 20 20 20 |
0,924 0,95—0,98 0,8 —0,9 0,895 0,932 |
|
Продолжение табл. 3
|
Для большинства реальных тел Є не постоянно и зависит от температуры, с ростом которой Є увеличивается.
При нагреве гладких неокисленных полированных поверхностей, имеющих малую степень черноты, вследствие окисления поверхности в интервале температур 200—400°С величина є резко увеличивается. Степень черноты шероховатых поверхностей во много раз больше степени черноты гладких полированных поверхностей.
Закон Кирхгофа. Согласно закону Кирхгофа, отношение излучательной способности Е к поглощательной А для всех тел одинаково равно излучательной способности абсолютно черного тела при той же температуре и зависит только от температуры.
Закон Кирхгофа выводится из рассмотрения лучистого теплообмена между абсолютно черной и серой пластинами, помещенными на небольшом расстоянии друг от друга. Температура обеих пластин одинакова, и, следовательно, теплообмен между ними отсутствует.
Серая поверхность излучает Е ккал/м2 • к энергии, которую черная поверхность полностью поглощает.
Черная поверхность излучает энергию в количестве Е0, Попадая на серую поверхность, эта энергия частично, в количестве АЕ0, поглощается, а остальная часть энергии в количестве
Ч’ ‘ •’ -‘vrv ЮГГГРГ*’ —♦ ^ •*
(1—А)Е0 отражается и полностью поглощается черной поверхностью, т. е. баланс лучистого обмена можно записать следующим образом:
Q = E — АЕ0ккал/м2-ч.
Как указывалось, при одинаковой температуре двух пластин <7 = 0 и, следовательно, математическое выражение закона Кирхгофа может быть представлено в следующем виде:
Е = АЕ0 или — = Еа.
0 Д 0 ■
Закон Ламберта (закон косинусов). Этот закон устанавливает, что лучеиспускательная способность в направлении под углом Еф (направление излучения составляет с нормалью к излучаемой поверхности угол ф) и лучеиспускательная способность поверхности в нормальном направлении Е„ связаны соотношением:
EV = Еп C0S ф-
Количество энергии, излучаемое элементом поверхности в направлении элемента DF, ориентированного под пространственным углом dQ и ф, определяется по формуле
DQф = Еп DQ Cos фDF1.
Величина излучения по нормали Еп может быть представлена в следующем виде:
Т. е. излучение по нормали в я раз меньше излучения по всем возможным направлениям. Тогда, подставив значение Еп, получим
DQ = —4,9 F—YdQdF, cos q>.
Ф я 100/ 1 т
Это уравнение является основой для расчета лучистого теплообмена между поверхностями конечных размеров.
|
Q = єпрС0ф |
Расчетные формулы для теплообмена излучением. Общая формула для расчета теплообмена излучением между двумя непрозрачными телами на основании закона Стефана — Больцмана (имеет вид
ІдюоУ vioo/J ‘
Где Q— количество тепла, переданное излучением от первого тела ко второму, в ккал/ч;
Єпр— приведенная степень черноты системы, учитывающая степень черноты обоих тел и их взаимное расположение;
С„— коэффициент лучеиспускания абсолютно черного тела, равный 4,96 ккал/м2-ч-°К4;
Ф— средний угловой коэффициент или коэффициент облученности, учитывающий форму, размеры и взаимное расположение поверхностей; — абсолютные температуры первого и второго тела
В °К
F— поверхность теплообмена в м2.
При расчете промышленных печей чаще всего встречается ‘следующее расположение тел:
А) две плоские параллельные неограниченные поверхности;
Б) две замкнутые поверхности произвольной формы, охватывающие одна другую;
В) две плоские поверхности, произвольно расположенные в пространстве одна относительно другой.
Значения величин єпр, ф и F могут быть определены теоретически и экспериментально с использованием метода моделирования.
При теплообмене излучением между двумя плоскими параллельными поверхностями ф = 1 и
— + —-1
El е2
Где и є2—степени черноты излучателя и нагреваемого
Тела
При расчете теплового излучения между двумя замкнутыми поверхностями F и F2, охватывающими одна другую (FjCFs), Ф=1; F в формуле. равна меньшей поверхности FІ и приведенная степень черноты системы
|
Где Fx — поверхность охватываемого тела в ж2; F3 — поверхность охватывающего тела в м2. |
Передача тепла излучением при произвольном расположении тел в пространстве производится по вышеприведенной формуле с введением в нее дополнительного множителя — среднего углового коэффициента фі.2і
|
Ft Fz |
Где и Fa — поверхности излучения двух произвольно расположенных тел в м2 Фх и ф2 — углы, образуемые направлением лучей с нормалями к поверхности излучающих тел; г—расстояние между двумя взаимно излучающими телами в м.
Так как вычисление среднего углового коэффициента по уравнению с двойным интегралом вызывает значительные трудности, то его обычно определяют графическим путем или по упрощенным формулам, учитывающим взаимное расположение и форму излучающих поверхностей. Эти графики и формулы приведены в специальной литературе по вопросам лучистого теплообмена.
Теплообмен между двумя плоскими поверхностями, произвольно расположенными в пространстве, рассматривается ниже. Значения епр могут быть определены и методом лучистого сальдо, предложенным Г. JI. Поляком. Сущность этого метода состоит в следующем.
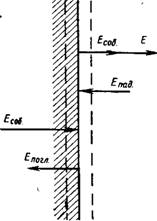
Результативный транзит лучистой энергии сквозь внешнюю поверхность тела может быть рассчитан двумя способами (рис. 6).
Сквозь правую контрольную поверхность (пунктирная линия) от тела уходит испускаемая им собственная энергия Есоб И отражаемая энергия ^отр • Сумма собственной и отражаемой энергий названа эффективной энергией £эф. Через ту же контрольную поверхность в сторону тела проходит падающая энергия £„ад.
|
= q + Es |
|
‘пад |
Если температура тела ниже температуры окружающей среды," то результативный транзит энергии равен превышению £пад над £эф и направлен в сторону тела. Это превышение, названное Г. JI. Поляком лучистым сальдо, является количеством тепла, полученным телом,
Я — -^пад Еэ
^пад — -"-эф или
Аналогично лучистое сальдо через иную контрольную поверхность может быть выражено следующим образом:
Я = £пог £соб = — А^пад Fcog,
|
Отр. |
|
Рис. 6. Схема для расчета результативного транзита лучистой энергии |
Где £пог— поглощаемая телом энергия.
Подставляя В последнюю формулу величину — Спад, получим п і р _ Д + Есоб
Р Д 4- £соб . Д 4- ^соб — ^<7 _
_ д(1-А) + Есоб =Ео+/±_1
А и ‘
В общем виде для тела, температура которого выше или ниже температуры окружающей среды, выражение для лучистого сальдо имеет вид:
£Эф = Ео ± Я (-J — — 1 ) •
Пользуясь методом лучистого сальдо, лег^о решить, например, задачу о передаче тепла между двумя параллельными пластинами.
Падающая энергия на одну пластину равна всей эффективной энергии другой пластины, т. е.
Я,ч — Еэф1 Еэф2′
Далее получаем
— £ол — Я^—L)- Е0- <72 ~ 1 ) , .
Причем
Яі = Яг = <7І,2>
Откуда
Ео.1
Аі+ А2 1
Или
Аг + A2
Следует также указать на понятия о цветовой и яркостной температурах.
Цветовой температурой Тц называется температура абсолютно черного тела, имеющего для двух определенных спектральных участков то же отношение яркостей, что в данное тело, имеющее температуру Т. Для всех металлов цветовая температура Гц выше, чем истинная температура тела Т.
Яркостной температурой Тя называется температура абсолютно черного тела, имеющего ту же визуальную монохроматическую яркость для определенной длины волны, что и данный излучатель, имеющий температуру Т. Яркостная температура всегда меньше истинной температуры тела.



 1 ноября, 2012
1 ноября, 2012  admin
admin 
 Опубликовано в рубрике
Опубликовано в рубрике