Задача распространения тепла в насыпи путем теплопроводности в случае пластового очага может быть сформулирована следующим образом: в неограниченной среде с начальной температурой Т0 В момент времени T=0 Начинает действовать плоский источник тепловыделения, удельная интенсивность которого является непрерывной функцией координаты Q=Q(X). Рассмотрим задачу определения температурных полей в дисперсной насыпи комбикормового сырья, которая решается численно и аналитически для разных значений переменных, характеризующих объект исследования: плотности Р, Удельной теплоемкости С, Ко-
68
Глава 3. Возникновение процессов горения
Эффициента теплопроводности ![]() Начальной температуры Т0, Размера оча
Начальной температуры Т0, Размера оча
га R, Его удельной мощности в центре Q0 И на периферии ![]() Теория подо
Теория подо
бия позволяет получить решение задачи, носящее обобщенный характер.
Применяя теорию обобщенных переменных, осуществим переход к без
размерным величинам: числу Фурье Т0, Безразмерной температуре ![]() , от
, от
носительному расстоянию Х* ‘
![]() (3.46)
(3.46)
Тогда математическая формула задачи имеет вид:
|
|
(3..47)
(3.48)
(3.49)
Применяя косинус-преобразование Фурье, получим дифференциальное уравнение
![]() (3.50)
(3.50)
Где ![]() (3.51)
(3.51)
Решением уравнения (3.50) при условии (3.48) является выражение
![]() (3.52) оригинал которого имеет вид
(3.52) оригинал которого имеет вид
(3.53)
![]()
В насыпи комбикормов распределение микрофлоры имеет случайный характер и удельную интенсивность тепловыделения можно представить в виде
(3.54)
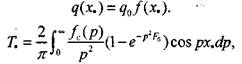 (3.55) где
(3.55) где ![]() (3.56)
(3.56)
69
Корольченко А. Я. Процессы горения и взрыва
Разлагая экспоненту в ряд получим:
![]() (3.57)
(3.57)
Где
![]() (3.58)
(3.58)
Решение (3.56) совпадает с решением задачи на охлаждение греющейся пластины в неограниченной среде в случае одинаковости теплофи-зических характеристик и начальных температур пластины и среды. Подставляя (3.46) в (3.56), получим решение в случае отсутствия фонового тепловыделения ![]()
![]() (3.59)
(3.59)
В стационарном случае наличия равномерного фонового разогрева с удельной мощностью ![]() Справедливо соотношение
Справедливо соотношение
|
|
(3.60)
Применяя принцип суперпозиции тепловых полей, получаем приближенную формулу для расчета распределения температуры в дисперсной насыпи при наличии фонового тепловыделения
![]() (3.61)
(3.61)
Где ![]() Согласно (3.60).
Согласно (3.60).
Расчет безразмерной относительной температуры ![]() ) вы-
) вы-
Полнен путем численного интегрирования уравнения (3.47) с начальным условием (3.48) и граничными условиями (3.49) для значений числа Фурье ![]() [0,05; 8] и относительного расстояния
[0,05; 8] и относительного расстояния ![]() [0; 15]. т. е. в области значе-
[0; 15]. т. е. в области значе-
Ний параметров, имеющей практический интерес. Значения ![]() Вычис-
Вычис-
Лялись согласно (3.56) для случая ![]() , что не меняет общности полч-ченных
, что не меняет общности полч-ченных
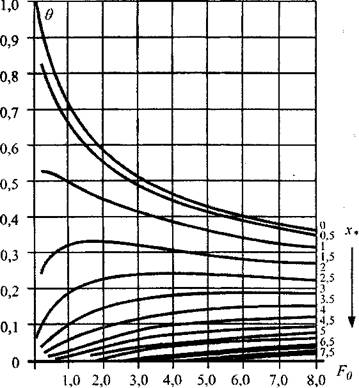
Результатов. В результате расчета построена номограмма ![]() представленная на Рис. 3.6, Позволяющая определить температурное поле в дисперсной насыпи комбикормового сырья путем использования соотношения (3.61). На рис.3.7 представлены расчетные кривые распределения температур в насыпи травяной муки, полученные по формуле (3.61) при различных параметрах очага. На Рис.3.8 Приведена номограмма изменения темпе-
представленная на Рис. 3.6, Позволяющая определить температурное поле в дисперсной насыпи комбикормового сырья путем использования соотношения (3.61). На рис.3.7 представлены расчетные кривые распределения температур в насыпи травяной муки, полученные по формуле (3.61) при различных параметрах очага. На Рис.3.8 Приведена номограмма изменения темпе-
70
Глава 3. Возникновение процессов горения
Ратуры в центре очага до пожароопасного значения (-100 °С) в зависимости от времени для разной интенсивности тепловыделения.
|
|
Рис. 3.6. Номограмма безразмерной относительной температуры для пластового очага (Fo ~ число Фурье).
|
|
|
(3.62) (3.63) (3.64) |
|
|
Гнездовый очаг. Задача нахождения температурных полей в случае гнездового очага сводится к решению симметричной задачи, которая в обобщенных переменных имеет вид:
|
|
Где относительная координата
71
Корольченко А. Я. Процессы горения и взрыва
|
|
Рис. 3.7. Температурные кривые при различных параметрах очаги для травяной муки (характеристики материала:
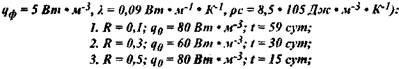
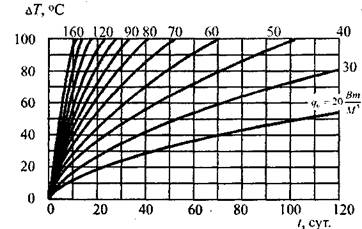
Рис. 3.8. Рост температуры В Центре пластового очага (R~0,3M.) прирахшчной интенсивности тепловыдаения (шроты, жмыхи).
Глава 3. Возникновение процессов горения
Задача решается численно совместно с уравнением
|
|
(3.65)
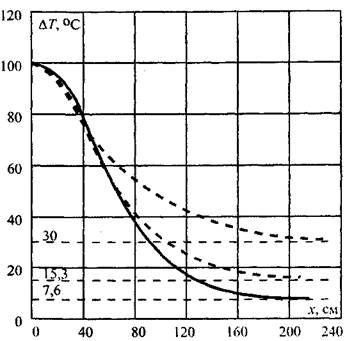
В результате чего построена номограмма ![]() ) для практически
) для практически
Важных значений параметров, позволяющая по формуле (3.61) определять распределение температур (рис. 3.9).
Предложенная математическая модель процесса самонагревания удовлетворительно согласуется с экспериментом. Так, На рис. 3.10 Представлены расчетные кривые и экспериментальные значения температур, полученные в
|
|
Рис. 3.9. Номограмма безразмерной относительной Температуры для гнездового очага (Fo — число Фурье).
73
Корольченко А. Я. Процессы горения и взрыва
Крупномасштабном эксперименте на фрагменте силоса размером 3x3x4,8 м. Некоторая ассиметрия температурных полей относительно плоскости Х=0, Соответствующей центру очага, связана с конвекцией нагретых паров воды и воздуха в верхнюю часть насыпи.
Адекватность модели эксперименту позволяет использовать ее для решения целого ряда прикладных задач: расчета радиуса чувствительности термодатчика, оценки эффективности система термоконтроля, расчета пожароопасности темпа роста температуры и пожаробезопасных сроков хранения сырья.
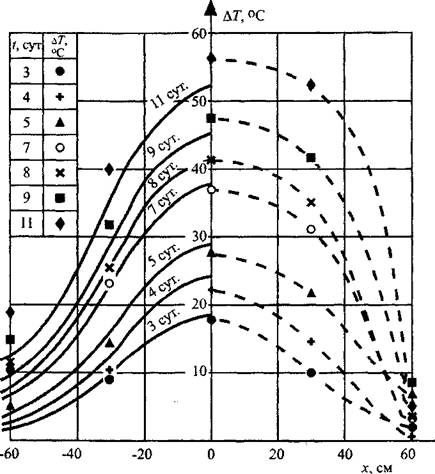
Рис. 3.10. Температурные поля при пластовом самонагревании Травяной муки (крупномасштабный эксперемент): Р*=470кг* м-3; R = 0,25 м; Q0 = 75 Вт ![]()
74
Глава 3. Возникновение процессов горения
Приближенное решение задачи самовозгорания дисперсных материалов для реакции порядка ![]() Самовозгорание мелкодисперсных органических материалов относится к одному из распространенных явлений, наблюдаемых в практике хранения, переработки и транспортировки веществ и материалов. Особенностью самовозгорания является то, что оно для своего появления и развития не требует внешнего импульса, инициирующего горение, или высоких температур. Это явление возникает за счет реакции гетерогенного окисления в больших объемах продукта при относительно низких температурах окружающей среды и сопровождается образованием газообразных продуктов реакции. Из-за плохой теплопроводности массы мелкодисперсного продукта происходит накопление тепла в объеме, возрастание температуры, скорости химической реакции и, в конечном счете, воспламенение материала.
Самовозгорание мелкодисперсных органических материалов относится к одному из распространенных явлений, наблюдаемых в практике хранения, переработки и транспортировки веществ и материалов. Особенностью самовозгорания является то, что оно для своего появления и развития не требует внешнего импульса, инициирующего горение, или высоких температур. Это явление возникает за счет реакции гетерогенного окисления в больших объемах продукта при относительно низких температурах окружающей среды и сопровождается образованием газообразных продуктов реакции. Из-за плохой теплопроводности массы мелкодисперсного продукта происходит накопление тепла в объеме, возрастание температуры, скорости химической реакции и, в конечном счете, воспламенение материала.
Практический интерес к процессам теплового взрыва обусловлен принципиальной возможностью заранее вычислить безопасные условия проведения переработки и хранения дисперсных материалов, при которых исключается самопроизвольное возникновение горения.
Математическая постановка задачи о тепловом взрыве в классической теории заключается в следующем: задается область (объем), внутри которой находится реагирующее вещество. Считаются известными физико-химические константы, характеризующие теплообмен и реакцию горения, механизм теплоотдачи внутри области, начальные и граничные условия.
Решение приближенной задачи определения условий самовозгорания дисперсных материалов при их окислении по реакции порядка ![]() И изменении в широком диапазоне параметров тепломассообмена сводится к известным уравнениям теплопроводности с распределенным источником тепла и скорости химической реакции
И изменении в широком диапазоне параметров тепломассообмена сводится к известным уравнениям теплопроводности с распределенным источником тепла и скорости химической реакции
|
|
(3.66)
|
|
(3.67)
Граничными и начальными условиями будут
|
|
(3.68)
75
Корольченко А. Я. Процессы горения и взрыва
(3.69)
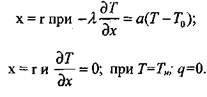 (3.70)
(3.70)
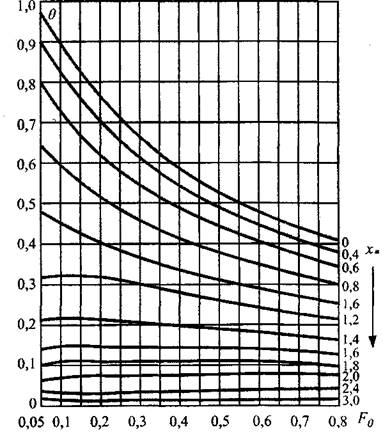
Уравнение (3.66) является уравнением теплопроводности с распределенными источниками тепла в насыпи материала, а уравнение (3.67) характеризует скорость химической реакции. Граничные условия формулируют отсутствие теплового потока на оси симметрии рассматриваемых объемов и теплообмен с окружающей средой по закону Ньютона. В задаче рассматриваются три симметричные области: плоскопараллельная (п = 0); цилиндрическая (п = 1); сферическая (п — 2), и приняты следующие обозначения: Тн, Т0, Т — начальная температура, температура окружающей среды и текущая температура в зоне реакции, соответственно; Х,R — Текущая координата и характерный размер, соответственно; T — время; Q ~ Тепловой эффект реакции; Е — энергия активации; К0 — Прсдэкспонент;
![]() ‘ — теплопроводность, теплоемкость и плотность вещества, соответственно; А — коэффициент теплоотдачи; R — газовая постоянная; С0 — концентрация окислителя в окружающей среде; Q — Количество тепла, выделяющегося в ходе реакции на единицу массы твердой фазы: Т,
‘ — теплопроводность, теплоемкость и плотность вещества, соответственно; А — коэффициент теплоотдачи; R — газовая постоянная; С0 — концентрация окислителя в окружающей среде; Q — Количество тепла, выделяющегося в ходе реакции на единицу массы твердой фазы: Т, ![]() — Порядок реакции по окислителю и горючему; А — Коэффициент теплоотдачи.
— Порядок реакции по окислителю и горючему; А — Коэффициент теплоотдачи.
Определим среднюю по объему температуру
![]() (3.71)
(3.71)
И приближенно учтем распределение температуры в виде параболы второго порядка где А и В — коэффициенты являющиеся функцией времени, которые определяются из граничных условий (3.68)-(3.70). Тогда средняя температура будет
|
|
(3.72)
Выразим уравнение (3.66) и (3.67) через среднюю температуру, для чего все члены этих уравнений умножим на X"»Dx И проинтегрируем от 0 до оо
|
|
(3.73)
76
Глава 3. Возникновение Процессов горения
|
|
(3.74)
Определим произведение АВ Через среднюю температуру ![]() . Из (3.69) и (3.99) найдем
. Из (3.69) и (3.99) найдем
|
|
(3.75)
Преобразуем (3.72) к виду
|
|
(3.76)
|
|
Получим, что
(3.77)
Подставляя (3.77) в (3.75) найдем, что
|
|
(3.78)
С Учетом (3.78) И Равенства критерия ![]() Система уравнений
Система уравнений
(3.66) и (3.67) перепишется в виде (знак осреднения опускаем)
|
|
(3.79)
(3.80)
Для того, Чтобы свести полученную систему уравнений к нашей задаче, преобразуем выражение ![]() В экспоненту
В экспоненту
|
|
Где
(3.81)
(3.82)
77
Корольченко А. Я. Процессы горения и взрыва
|
|
В безразмерных переменных (3.66) и (3.67) с учетом (3.81) перепишется в виде
(3.83)
Где
(3.84)
![]()
|
|
(3.85)
|
|
(3.86)
|
|
(3.87)
|
|
(3.88)
|
|
(3.89)
Полученная система уравнений определяет критическое условие самовозгорания:
![]()
С учетом принятых обозначений можно записать
(3.90)
|
|
(3.91)
78
Глава 3. Возникновение процессов горения
Полученное критическое условие отличается членом
|
|
(3.92)
Который учитывает неоднородность распределения температуры в оо-разце.
Анализ уравнения (3.92) показывает, что оно дает несколько завышенные значения по сравнению с решением Франк-Каменецкого. Введением в уравнение (3.92) согласующей функции Ф(ВI) (рис.3.11),
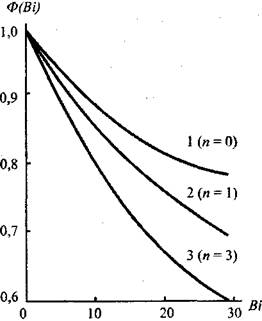
Рис 3.11. Зависимость функции Ф(Bi) от ВI: 1 — плита, 2 — Циллиндр, 3 — Сфера
Значения которой рассчитаны по экспериментальным данным, достигается удовлетворительное согласие с решением задачи Франк-Каменецкого во всем диапазоне изменения параметра ВI (от 0 до со)
|
|
(3.93)
79
Корольченко А. Я. Процессы горения и взрыва
Таблица 3.2
Критические условия хранения различных видов Растительного сырья
|
№ п/п |
Наименование продукта |
|
|
|
|
|
|
|
|||
|
1 |
Травяная мука |
121-1015 |
117 |
1,75 |
357,73 |
— |
329,45 |
— |
318,53 |
— |
36 |
|
2 |
Шрот подсолнечный |
3,79- 106 |
43,2 |
2,27 |
267,61 |
2,4 |
225,92 |
2,2 |
211,84 |
2,2 |
0,39 |
|
3 |
Жмых подсолнечный |
1,51 106 |
42,0 |
1,2 |
274,44 |
4 |
229,48 |
3,6 |
214,50 |
3,5 |
0,5 |
|
4 |
Шрот соевый |
4,36- 109 |
47,3 |
1,85 |
292,61 |
13 |
247,03 |
9,2 |
231,64 |
9,1 |
0,8 |
|
5 |
Мука пшеничная |
1,94- 1010 |
81,2 |
3,02 |
348,88 |
— |
310,45 |
— |
296,42 |
1387, 6 |
8,4 |
|
6 |
Отруби пшеничные |
4,1 108 |
60,9 |
2,27 |
303,05 |
264,66 |
17,7 |
251,01 |
17,2 |
1,12 |
|
|
7 |
Мука из ячменя |
2,04-109 |
73,6 |
2,61 |
344,91 |
— |
303,61 |
— |
288,76 |
548,1 |
5,63 |
|
8 |
Дрожжи кормовые |
7,93- 10ю |
83,4 |
3,35 |
340,15 |
304,53 |
291,41 |
650,6 |
6,25 |
||
|
9 |
Комбикорм для свиней |
8,89′ 10й |
93,5 |
1,41 |
352,05 |
317,92 |
305,18 |
8,1 |
|||
|
10 |
Комбикорм для птиц |
3,79- 109 |
71,6 |
1,78 |
326,35 |
288,31 |
136 |
274,57 |
120,6 |
2,8 |
80
Глава 3, Возникновение процессов горения
Учет функции Ф(Bi) В уравнении (3.93) позволяет существенно уменьшить неточность, возникающую в результате апроксимации распределения температуры в горючей системе параболой второго порядка.
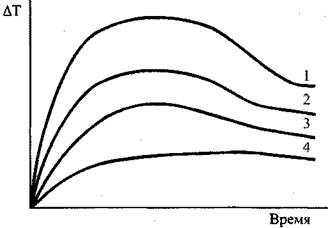
Рис. 3.12. Кинетические кривыеразогревов: 1-447 К; 2-450 К, 3-456; 4-458.
Для расчета критических значений температуры (T) и характерного размера (r) в уравнении (3.93) необходимы значения величин кинетических параметров: Е, Ко И v. (определение этих параметров осуществляется графоаналитическим способом по методу термического анализа из экспериментальных кривых " ![]() — время" (Рис. 3.12).
— время" (Рис. 3.12).
Разработанная математическая модель позволяет рассчитывать условия самовозгорания и выполнить прогноз поведения насыпей дисперсной горючей массы любого размера и любой формы.
Результаты расчетов для широкого круга продуктов растительного происхождения представлены в табл. 3.2.
Данные табл. 3.2 показывают, что благодаря предложенной схеме расчета условие теплового самовозгорания можно не только установить ряд потенциальной опасности различных видов горючего дисперсного материала, но и прогнозировать критические условия их хранения (время индукции, размеры насыпи).
Необходимость обработки большого числа термических кривых делает описанный метод достаточно трудоемким и затрудняет его использование для быстрого получения необходимой информации. В связи с этим
81
Корольченко А. Я. Процессы Горения и взрыва______________________
Разрабоганы алгоритмы и программа для расчета критических параметров на персональной ЭВМ. Это позволяет оперативно рассчитывать критические параметры процесса самовозгорания дисперсных горючих материалов и осуществлять прогноз их поведения в процессе переработки, транспортировки и хранения.
Таблица 3.3. Сравнение расчетных и экспериментальных значений температуры
Самовозгорания.
|
Наименование материала |
Размер Образца, М |
Температура, °С |
|
|
|
Расчет, tp |
Эксперимент, tэ |
|||
|
Торф шатурский |
0,05 |
128,0 |
139,0 |
11,0 |
|
Шрот хлопковый |
0,05 |
147,0 |
150,0 |
2,5 |
|
Опилки древесные сосновые |
0,05 |
166,0 |
170,0 |
3,4 |
|
Мука пшеничная (сорт высший) |
0,05 |
173,4 |
178,0 |
4,6 |
|
Шрот соевый |
0,8 |
57,1 |
59,0 |
1,9 |
Проверка точности выбранной расчетной модели условий теплового самовозгорания дисперсных горючих материалов осуществлялась на лабораторной и полигонной установке.
В лабораторных условиях исследовался разогрев материала с целью получения зависимости T=F(T) И определения кинетических характеристик. На полигонной установке изучался процесс самовозгорания в условиях, приближенных к реальному хранению материалов.
Результаты сопоставления расчета с экспериментом представлены в Табл. 3.3, из которых следует возможность прогноза условий теплового самовозгорания по рассмотренной выше методике с достаточной для практических целей точностью.
82



 5 мая, 2013
5 мая, 2013  admin
admin 
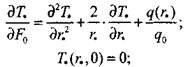
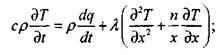
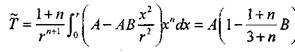
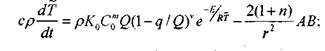
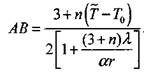
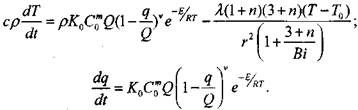
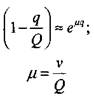
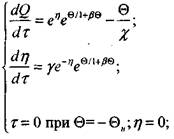
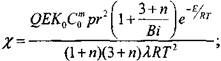
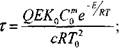
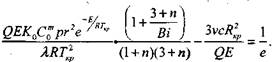
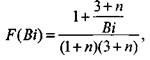
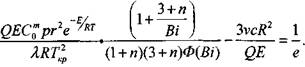
 Опубликовано в рубрике
Опубликовано в рубрике