5.1 Converting liquid flow in lb/h to gpm, and vice versa; relating density, specific gravity, and specific volume
5.2 Relating head of liquid or gas column to pressure; converting feet of liquid to psi; relating inches of water column of gas to psi and feet of gas column
5.3 Estimating density of gases; relating molecular weight and density; effect of elevation on gas density; simplified formula for density of air and flue gases at sea level
5.4 Relating actual and standard cubic feet of gas per minute to lb/h
5.5 Computing density of gas mixture; relating mass to volumetric flow; computing velocity of gas in duct or pipe
5.6 Relating mass and linear velocities
5.7 Calculating velocity of wet and superheated steam in pipes; computing specific volume of wet steam; use of steam tables
5.8 Relating boiler horsepower to steam output
5.9 Calculating amount of moisture in air; relative humidity and saturation vapor pressure
5.10 Water dew point of air and flue gases; partial pressure of water vapor
5.11 Energy absorbed by wet and superheated steam in boilers; enthalpy of wet and dry steam; use of steam tables; converting MM Btu/h (million Btu/h) to kilowatts
5.12 Relating steam by volume, steam by weight, and steam quality; relating circulation ratio and quality 5.13a Determining steam quality using throttling calorimeter 5.13b Relating steam quality to steam purity
5.14 Water required for desuperheating steam; energy balance in attemperators, desuperheaters
5.15 Water required for cooling gas streams
5.16 Calculating steam volume after throttling process; use of steam tables
5.17 Determining blowdown and steam for deaeration
5.18 Calculating flash steam from boiler blowdown; economics of flash steam recovery
5.19a Estimating leakage of steam through openings; effect of wetness of steam on leakage
5.19b Estimating air flow through openings
5.20 Estimating leakage of gas across dampers; calculating energy loss of leakage flow; sealing efficiency of dampers on area and flow basis
5.21 Economics of waste heat recovery; annual cost of energy loss; simple payback period calculation
5.22 Life-cycle costing applied to equipment selection; interest and escalation factors; capitalized and life-cycle cost
5.23 Life-cycle costing applied to evaluation of heat recovery systems
5.24 Calculating thickness of boiler tubes to ASME Code; allowable stresses for various materials
5.25 Calculating maximum allowable working pressures for pipes
5.26 Sizing tubes subject to external pressure
5.27 On sound levels: OSHA permissible exposure levels
5.28 Adding decibels
5.29 Relating sound pressure and power levels
5.30 Effect of distance on noise level
5.31 Computing noise levels from engine exhaust
5.32 Holdup time in steam drum
5.01
Q:
Convert 50,000 lb/h of hot water at a pressure of 1000 psia and 390°F to gpm. A:
To convert from lb/h to gpm, or vice versa, for any liquid, we can use the following expressions:
W = 8 — (1)
V
P = 62.4s = — (2)
V
Where
W = flow, lb/h
Q = flow, gpm (gallons per minute) p = density of liquid, lb/cu ft s = specific gravity of liquid v = specific volume of liquid, cu ft/lb
For hot water we can obtain the specific volume from the steam tables (see the Appendix). v at 1000psia and 390°F is 0.0185 cu ft/lb. Then, from Eq. (1),
0.0185
Q = 50,000 x —-— = 115.6 gpm
8
Estimate the head in feet developed by a pump when it is pumping oil with a specific gravity of 0.8 through a differential pressure of 150 psi.
Conversion from feet of liquid to psi, or vice versa, is needed in pump calculations. The expression relating the variables is
DP
H = 144 DPv = 2.3— (3)
S
Where
DP = differential pressure, psi H = head, ft of liquid
Substituting for DP and s, we have
H, = 2.3 x — = 431.2 ft
1 0.8
If a fan develops 8 in. WC (inches of water column) with a flue gas density of 0.05 lb/cu ft, what is the head in feet of gas and in psi?
Use the expressions DP
Hg = 144— (4)
G Pg
Hw = 27.7DP (5)
Where
Hg = head, ft of gas Hw = head, in. WC pg = gas density, lb/cu ft
Combining Eqs. (4) and (5), we have 8
Hg = 144 x——————— = 835 ft
G 27.7 x 0.05
8
DP = -— = 0.29 psi
27:7
Estimate the density of air at 5000 ft elevation and 200°F.
The density of any gas can be estimated from
P
Pg = 492 x MW x———— ———- ———————————————— (6)
Fg 359 x (460 + t) x 14.7 V 7
Where
P = gas pressure, psia MW = gas molecular weight (Table 5.1) t = gas temperature, °F pg = gas density, lb/cu ft
The pressure of air decreases as the elevation increases, as shown in Table 5.2, which gives the term (P/14.7) x MW of air = 29. Substituting the various terms, we have
0 832
Pg = 29 x 492 x——- .——- = 0.05 lb/cu ft
Fg 359 x 660 ‘
|
TAble 5.1 Gas Molecular Weights
|
A simplified expression for air at atmospheric pressure and temperature t at sea level is
40
Pg 460 +1 ( )
For a gas mixture such as flue gas, the molecular weight (MW) can be obtained as discussed in Q5.05. In the absence of data on flue gas analysis, Eq. (7) also gives a good estimate of density.
|
Table 5.2 Density Correction for Altitude
|
When sizing fans, it is the usual practice to refer to 70°F and sea level as standard conditions for air or flue gas density calculations.
5.04A Q:
How is acfm (actual cubic feet per minute) computed, and how does it differ from scfm (standard cubic feet per minute)?
Acfm is computed using the density of the gas at given conditions of pressure and temperature, and scfm is computed using the gas density at 70°F and sea level (standard conditions).
W
Q=^ (8)
6°pg
Where
Q = gas flow in acfm (at 70°F and sea level, scfm and acfm are equal; then q = W/4.5)
Pg = gas density in lb/cu ft (at standard conditions pg = 0.075 lb/cu ft) W = gas flow in lb/h = 4.5q at standard conditions
Convert 10,000 lb/h of air to scfm.
Using Eq. (6), it can be shown that at P = 14.7 and t = 70, for air pg = 0.075 lb/cu ft.
Hence, from Eq. (8),
1. f
Q =—————- = 2222 scfm
60 0:075
Convert 3000 scfm to acfm at 35 psia and 275°F. What is the flow in lb/h? The fluid is air.
Calculate the density at the actual conditions.
35
P g = 29 x 492 x————————— = 0.129 lb/cu ft
Fg 359 x 735 x 14.7 ‘
From the above,
W = 4.5 x 3000 = 13,500 lb/h
Hence
13,500
Acfm = 60^7129 = 1744 cfm
5.05 Q:
In a process plant, 35,000lb/h of flue gas having a composition N2 = 75%,
O2 = 2%, CO2 = 15%, and H2O = 8%, all by volume, flows through a duct of cross section 3 ft2 at a temperature of 350°F. Estimate the gas density and velocity. Because the gas pressure is only a few inches of water column, for quick estimates the gas pressure may be taken as atmospheric.
To compute the density of a gas, we need its molecular weight. For a gas mixture, molecular weight is calculated as follows:
MW = ]T(MW,- x y)
Where
Y, = volume fraction of gas i MW,- = molecular weight of gas i
Hence
MW = 0.75 x 28 + 0.02 x 32 + 0.15 x 44 + 0.08 x 18 = 29.68
From Eq. (6),
492
Pg = 29.68 x—————- = 0.05 lb/cu ft
359 x 810
|
Vg=— (9) |
![]() The gas velocity Vg can be obtained as
The gas velocity Vg can be obtained as
60 p gA
|
Where |
![]() Vg = velocity, fpm (feet per minute) — 2 A = cross section, ft
Vg = velocity, fpm (feet per minute) — 2 A = cross section, ft
Hence
35,000
V g = 2 = 3888 fpm
G 60 x 0.05 x 3
The normal range of air or flue gas velocities in ducts is 2000-4000 fpm. Equation (9) can also be used in estimating the duct size.
In the absence of flue gas analysis, we could have used Eq. (7) to estimate the gas density.
5.06 Q:
A term that is frequently used by engineers to describe the gas flow rate across heating surfaces is gas mass velocity. How do we convert this to linear velocity? Convert 5000 lb/ft2 h of hot air flow at 130°F and atmospheric pressure to fpm.
|
G_ 60Pg |
![]() Use the expression
Use the expression
V g = — (10)
Where G is the gas mass velocity in lb/ft2 h. Use Eq. (7) to calculate pg 40
P-=460+T30 =00678 lb/cu ft
Hence
5000
Vg =—————— = 1230 fpm
G 60 x 0.0678 p
What is the velocity when 25,000 lb/h of superheated steam at 800 psia and 900°F flows through a pipe of inner diameter 2.9 in.?
Use expression (11) to determine the velocity of any fluid inside tubes cylindrical ducts.
|
, pipes, or |
![]()
|
(11) |
![]() V
V
V = 0.05 x W x
Where
V = velocity, fps
V = specific volume of the fluid, cu ft/lb d, = inner diameter of pipe, in.
For steam, v can be obtained from the steam tables in the Appendix.
V = 0.9633 cu ft/lb
Hence
0.9633
V = 0.05 x 25,000 x — = 143 fps
2.92
The normal ranges of fluid velocities are
Water: 3-12 fps Steam: 100-200 fps
Estimate the velocity of 70% quality steam in a 3 in. schedule 80 pipe when the flow is 45,000 lb/h and steam pressure is 1000 psia.
We need to estimate the specific volume of wet steam.
V = xvg + (1 — x)vf
Where vg and vf are specific volumes of saturated vapor and liquid at the pressure in question, obtained from the steam tables, and x is the steam quality (see Q5.12 for a discussion of x). From the steam tables, at 1000psia, vg = 0.4456 and vf = 0.0216 cu ft/lb. Hence the specific volume of wet steam is
V = 0.7 x 0.4456 + 0.3 x 0.0216 = 0.318 cu ft/lb
The pipe inner diameter d, from Table 5.3 Is 2.9 in. Hence, from Eq. (11),
V = 0.05 x 45,000 x 0318 = 85 fps
2.92
What is meant by boiler horsepower? How is it related to steam generation at different steam parameters?
Packaged fire tube boilers are traditionally rated and purchased in terms of boiler horsepower (BHP). BHP refers to a steam capacity of 34.5 lb/h of steam at atmospheric pressure with feedwater at 212°F. However, a boiler plant operates at different pressures and with different feedwater temperatures. Hence conversion between BHP and steam generation becomes necessary.
W = 33^ C2)
Where
Ah = enthalpy absorbed by steam and water = (hg — hfw) + BD (hf — h^)
Where
Hg = enthalpy of saturated steam at operating steam pressure, Btu/lb hf = enthalpy of saturated liquid, Btu/lb h^ = enthalpy of feedwater, Btu/lb BD = blowdown fraction
For example, if a 500BHP boiler generates saturated steam at 125psig with 5% blowdown and with feedwater at 230°F, the steam generation at 125 psig will be
500 x 33,475
W =
(1193 — 198) + 0.05 x (325 — 198) = 16,714 lb/h
Where 1193, 198, and 325 are the enthalpies of saturated steam, feedwater, and saturated liquid, respectively, obtained from steam tables. (See Appendix.)
Why do we need to know the amount of moisture in air?
In combustion calculations (Chap. 6) we estimate the quantity of dry air required to burn a given amount of fuel. In reality, atmospheric air is never dry; it consists of some moisture, depending on the relative humidity and dry bulb temperature. To compute the partial pressure of water vapor in the flue gas, which is required
|
TAble 5.3 Dimensions of Iron Steel Pipe (IPS)
|
|
ACommonly known as standard. bCommonly known as extra heavy. cApproximately. |
For calculating nonluminous heat transfer, we need to know the total quantity of water vapor in flue gases, a part of which comes from combustion air.
Also, when atmospheric air is compressed, the saturated vapor pressure (SVP) of water increases, and if the air is cooled below the corresponding water dew point temperature, water can condense. The amount of moisture in air or gas fixes the water dew point, so it is important to know the amount of water vapor in air or flue gas.
Estimate the pounds of water vapor to pounds of dry air when the dry bulb temperature is 80°F and the relative humidity is 65%.
M = 0.622 x —pw——— (13)
14.7 — pw
Where
M lb water vapor/lb dry air
Pw partial pressure of water vapor in air, psia
This may be estimated as the vol% of water vapor x total air pressure or as the product of relative humidity and the saturated vapor pressure (SVP). From the steam tables we note that at 80°F, SVP = 0.5069 psia (at 212°F, SVP = 14.7 psia). Hence pw 0.65 x 0.5069.
0.5069
M = 0.622 x 0.65 x——————————— = 0.0142
14.7 — 0.65 x 0.5069
Hence, if we needed 1000 lb of dry air for combustion, we would size the fan to deliver 1000 x 1.0142= 1014.2 lb of atmospheric air.
What is the water dew point of the flue gases discussed in Q5.05?
The partial pressure of water vapor when the vol% is 8 and total pressure is 14.7 psia will be
Pw = 0.08 x 14.7 = 1.19 psia
From the steam tables, we note that the saturation temperature corresponding to 1.19psia is 107°F. This is also the water dew point. If the gases are cooled below this temperature, water can condense, causing problems.
What is the water dew point of compressed air when ambient air at 80°F,
14.7psia, and a relative humidity of 65% is compressed to 35 psia?
Use the following expression to get the partial pressure of water vapor after compression:
|
|
Pw = partial pressure, psia P = total pressure, psia
The subscripts 1 and 2 stand for initial and final conditions. From Q5.09b, pw1 = 0.65 x 0.5069.
35
Pw2 = 0.65 x 0.5069 x — = 0.784 psia
From the steam tables, we note that corresponding to 0.784 psia, the saturation temperature is 93°F. This is also the dew point after compression. Cooling the air to below 93°F would result in its condensation.
Calculate the energy absorbed by steam in a boiler if 400,000 lb/h of superheated steam at 1600 psia and 900°F is generated with feedwater at 250°F. What is the energy absorbed, in megawatts?
The energy absorbed is given by
|
(15) |
![]() Q = W x (h2 — h1) (neglecting blowdown)
Q = W x (h2 — h1) (neglecting blowdown)
Where
W = steam flow, lb/h h2, hj = steam enthalpy and water enthalpy, Btu/lb
Q = duty, Btu/h
From the steam tables, h2 = 1425.3 Btu/lb and hj = 224 Btu/lb.
Q = 400,000 x (1425.3 — 224)
= 480.5 x 106 Btu/h = 480.5 million Btu/h (MM Btu/h)
Using the fact that 3413 Btu/h = 1 kW, we have
106
Q = 48(X5 X 3413^K)3=141MW
Estimate the energy absorbed by wet steam at 8G% quality in a boiler aT 16GG Psia when the feedwater temperature is 25G0F.
The enthalpy of wet steam can be computed as
H = xhg + (1 — x)h/ (16)
Where h is the enthalpy in Btu/lb. The subscripts g and/ stand for saturated vapor and liquid at the referenced pressure, obtained from saturated steam properties. x is the steam quality fraction.
From the steam tables, hg = 1163 Btu/lb and h/ = 624 Btu/lb at 16GG psia. The enthalpy of feedwater at 25G0F is 226 Btu/lb.
H2 = G.8 x 1163 + G.2 x 624 = 1G54 Btu/lb hj = 226 Btu/lb Q = 1G54 — 226 = 828 Btu/lb
If steam flow were 4GG, GGG lb/h, then
Q = 4GG, GGG x 828 = 331 x 1G6 = 331 MM Btu/h
How is the wetness in steam specified? How do we convert steam by volume (SBV) to steam by weight?
A steam-water mixture is described by the term quality, x, or dryness fraction.
X = 80% means that in 1 lb of wet steam, 0.8 lb is steam and 0.2 lb is water. To
Relate these two terms, we use the expression
100
SBV = 1 + [(100 — x)/x]x vf /vg (17)
Where
Vf, vg = specific volumes of saturated liquid and vapor, cu ft/lb x = quality or dryness fraction
From the steam tables at 1000 psia, Vf = 0.0216 and vg = 0.4456 cu ft/lb.
TOC o "1-5" h z Sbv ________________ 100___________________ 98 8%
_ 1 + [(100 — 80)/80] x 0.0216/0.4456 _ ‘
Circulation ratio (CR) is another term used by boiler engineers to describe the steam quality generated.
CR =1 (18)
x
A CR of 4 means that the steam quality is 0.25 or 25%; in other words, 1 lb of mixture would have 0.25 lb of steam and the remainder would be water.
How is the quality of steam determined using a throttling calorimeter?
Throttling calorimeters (Fig. 5.1) are widely used in low pressure steam boilers for determining the moisture or wetness (quality) of steam. A sampling nozzle is located preferably in the vertical section of the saturated steam line far from bends or fittings. Steam enters the calorimeter through a throttling orifice and passes into a well-insulated expansion chamber. Knowing that throttling is an isoenthal — pic process, we can rewrite Eq. (16) for enthalpy balance as
Hs = hm = xhg + (1 — x)hf
Where
Hs, hm, hf, hg = enthalpies of steam, mixture, saturated liquid, and saturated steam, respectively x = steam quality fraction
|
FIgure 5.1 Throttling calorimeter. |
The steam temperature after throttling is measured at atmospheric pressure, and then the enthalpy is obtained with the help of steam tables. The steam is usually in superheated condition after throttling.
A throttling calorimeter measures a steam temperature of 250°F when connected to a boiler operating at 100 psia. Determine the steam quality.
Solution. hs at atmospheric pressure and at 250°F = 1168.8 Btu/lb from steam tables; hg = 1187.2 and hf = 298.5 Btu/lb, also from steam tables. Hence
1168.8 = 1187.2x + (1 — x)298.5
Or
X = 0.979 or 97.9% quality
How is steam quality related to steam purity?
Steam purity refers to the impurities in wet steam, in ppm. A typical value in low pressure boilers would be 1 ppm of solids. However, quality refers to the moisture in steam.
The boiler drum maintains a certain concentration of solids depending on ABMA or ASME recommendations as discussed in Q5.17. If at 500psig pressure the boiler water concentration is 2500 ppm, and if steam should have 0.5 ppm solids, then the quality can be estimated as follows:
0.5
% Moisture in steam = x 100 = 0.02%
Or
Steam quality = 100 — 0.02 = 99.98%
5.14 Q:
How do we estimate the water required for desuperheating steam? Superheated steam at 700 psia and 800°F must be cooled to 700°F by using a spray of water at 300°F. Estimate the quantity of water needed to do this.
From an energy balance across the desuperheater, we get
W hj + Whf = W2 h2 (19a)
Where
Wj, W2 = steam flows before and after desuperheating W = water required h1, h2 = steam enthalpies before and after the process hf enthalpy of water
Also, from mass balance,
W2 = W1 + W
Hence we can show that
W=W2 x hi—^ (19b)
H1 — hf
Neglecting the pressure drop across the desuperheater, we have from the steam tables h1 = 1403, h2 = 1346, and hf = 271, all in Btu/lb. Hence W/W2 = 0.05. That is, 5% of the final steam flow is required for injection purposes.
Q:
How is the water requirement for cooling a gas stream estimated? Estimate the water quantity required to cool 100,000 lb/h of flue gas from 900°F to 400°F. What is the final volume of the gas?
A:
From an energy balance it can be shown [1] that
Q = 5.39 x 10—4 x (tj — t2)
W (20)
X 1090 + 0.45 x (t2 — 150)
Where
Q = water required, gpm t1, t2 = initial and final gas temperatures, °F W = gas flow entering the cooler, lb/h
Substitution yields
Q = 5.39 x 10—4 x (900 — 400)
100,000 x 1090 + 0.45 x (400 — 150)
= 23 gpm
The final gas volume is given by the expression
(460 + "-K256! + 0J41)
The final volume is 43,000 acfm.
5.16
Q:
In selecting silencers for vents or safety valves, we need to figure the volume of steam after the throttling process. Estimate the volume of steam when 60,000 lb/h of superheated steam at 650 psia and 800°F is blown to the atmosphere through a safety valve.
A:
We have to find the final temperature of steam after throttling, which may be considered an isoenthalpic process; that is, the steam enthalpy remains the same at 650 and 15 psia.
From the steam tables, at 650psia and 800°F, h= 1402Btu/lb. At 15psia (atmospheric conditions), the temperature corresponding to an enthalpy of 1402Btu/lb is 745°F. Again from the steam tables, at a pressure of 15psia and a temperature of 745°F, the specific volume of steam is 48 cu ft/lb. The total volume of steam is 60,000 x 48 = 2,880,000 cu ft/h.
5.17 Q:
How do we determine the steam required for deaeration and boiler blowdown water requirements?
Steam plant engineers have to frequently perform energy and mass balance calculations around the deaerator and boiler to obtain the values of makeup water, blowdown, or deaeration steam flows. Boiler blowdown quantity depends on the total dissolved solids (TDS) of boiler water and the incoming makeup water. Figure 5.2 shows the scheme around a simple deaerator. Note that there could be several condensate returns. This analysis does not consider venting of steam from the deaerator or the heating of makeup using the blowdown water. These refinements can be done later to fine-tune the results.
The American Boiler Manufacturers Association (ABMA) and ASME provide guidelines on the TDS of boiler water as a function of pressure (see Tables 5.4 And 5.5. The drum solids concentration can be at or less than the value shown in these tables. Plant water chemists usually set these values after reviewing the complete plant chemistry.
A
|
|
-e
50.000
|
DA |
![]() M
M
|
|
|
B |
Figure 5.2 Scheme of deaeration system.
|
TABLE 5.4 Suggested Water Quality Limitsa
|
N. d. = not detectable; n. s. = not specified.
ANo values are given for saturated steam purity target because steam purity achievable depends upon many variables, including boiler water total alkalinity and specific conductance as well as design of boiler, steam drum internals, and operating conditions (see footnote i). Because boilers in this category require a relatively high degree of steam purity, other operating parameters must be set as low as necessary to achieve this high purity for protection of the superheaters and turbines and/or to avoid process contamination. bWith local heat fluxes > 473.2 kW/m2 (> 150,000 Btu/h ft2), use values for the next higher pressure range.
CBoilers below 6.21 MPa (900 psig) with large furnaces, large steam release space, and internal chelant, polymer, and/or antifoam treatment can sometimes tolerate higher levels of feedwater impurities than those in the table and still achieve adequate deposition control and steam purity. Removal of these impurities by external pretreatment is always a more positive solution. Alternatives must be evaluated as to practicality and economics in each case.
DValues in table assume the existence of a deaerator.
ENonvolatile TOCs are the organic carbon not intentionally added as part of the water treatment regime.
FMaximum total alkalinity consistent with acceptable steam purity. If necessary, should override conductance as blowdown control parameter. If makeup is demineralized water at 4.14-6.89 MPa (600-1000 psig), boiler water alkalinity and conductance should be that in table for 6.90- 10.34MPa (1001-1500psig) range.
G‘‘Not detectable” in these cases refers to free sodium or potassium hydroxide alkalinity. Some small variable amount of total alkalinity will be present and measurable with the assumed congruent or coordinated phosphate pH control or volatile treatment employed at these high pressure ranges.
HMinimum level of OH~ alkalinity in boilers below 6.21 MPa (900 psig) must be individually specified with regard to silica solubility and other components of internal treatment.
Maximum values are often not achievable without exceeding suggested maximum total alkalinity values, especially in boilers below 6.21 MPa (900 psig) with > 20% makeup of water whose total alkalinity is > 20% of TDS naturally or after pretreatment with soda lime or sodium cycle ionexchange softening. Actual permissible conductance values to achieve any desired steam purity must be established for each case by careful steam purity measurements. Relationship between conductance and steam purity is affected by too many variables to allow its reduction to a simple list of tabulated values.
Source: Adapted from ASME 1979 Consensus.
A boiler generates 50,000 lb/h of saturated steam at 300psia, out of which
10,0 lb/h is taken for process and returns to the deaerator as condensate at 180°F. The rest is consumed. Makeup water enters the deaerator at 70°F, and steam is available at 300psia for deaeration. The deaerator operates at a pressure of 25 psia. The blowdown has a total dissolved solids (TDS) of 1500 ppm, and the makeup has 100 ppm TDS.
Evaluate the water requirements for deaeration steam and blowdown.
So/wft’on. From mass balance around the deaerator,
10,0 + D + M = F= 50,000 + B (21)
|
Table 5.5 Recommended Boiler Water Limits and Associated Steam Purity at Steady-State Full Load Operation—Water Tube Drum-Type Boilers
N. a. = not available. AActual values within the range reflect the TDS in the feedwater. Higher values are for high solids in the feedwater, lower values for low solids. BActual values within the range are directly proportional to the actual value of TDS of boiler water. Higher values are for the high solids in the boiler water, lower values for low solids. cThese values are exclusive of silica. dDictated by boiler water treatment. Source: American Boiler Manufacturers Association, 1982. |
From an energy balance around the deaerator,
10.0 x 148 + 1202.8 x D + M x 38 = 209 x F = 209 x (50,000 + B)
(22)
From a balance of solids concentration,
100 x M = 1500 x B (23)
D + M = 40,000 + B (24)
Substituting (23) into (24),
D + 15B = 40,000 + B2
Or
D + 14B = 40,000 (25)
From (22),
1.480.0 + 1202.8D + 38 x 15B = 209 x 50,000 + 209B
Solving this equation, we have B = 2375 lb/h, D = 6750 lb/h, M = 35,625 lb/h, and F = 52,375 lb/h. Considering venting of steam from the deaerator to expel dissolved gases and the heat losses, 1-3% more steam may be consumed.
5.18
Q:
How can the boiler blowdown be utilized? A 600 psia boiler operates for 6000 h annually and discharges 4000 lb/h of blowdown. If this is flashed to steam at 100 psia, how much steam is generated? If the cost of the blowdown system is $8000, how long does payback take? Assume that the cost of steam is $2/1000 lb.
To estimate the flash steam produced we may use the expression
H = xhg + (1 — x)hf (26)
Where
H = enthalpy of blowdown water at high pressure, Btu/lb hg, hf = enthalpies of saturated steam and water at the flash pressure, Btu/lb
X = fraction of steam that is generated at the lower pressure
From the steam tables, at 600psia, h = 471.6, and at 100psia, hg = 1187 and hf = 298, all in Btu/lb. Using Eq. (26), we have
471.6 = 1187x + (1 — x) x 298
Or
X = 0.195
About 20% of the initial blowdown is converted to flash steam, the quantity being 0.2 x4000 = 800lb/h. This 800lb/h of 100psia steam can be used for process. The resulting savings annually will be 6000
800 x 2 x — = $9600
Simple payback will be 8000/9600 = 0.8 year or about 10 months.
Tables are available that give the flash steam produced if the initial and flash pressures are known. Table 5.6 is one such table.
Estimate the leakage of steam through a hole 1/8 in. in diameter in a pressure vessel at 100psia, the steam being in a saturated condition.
The hourly loss of steam in lb/h is given by [2]
AP , ,
W = 50 1 + 0.00065(, — ,,) (27)
Where
W = steam leakage, lb/h
0 hole area, in.2
P steam pressure, psia,, ,sat steam temperature and saturated steam temperature, °F
|
Initial |
Temp. of liquid (oF) |
Atm. Pressure |
Percent of flash at reduced pressures |
|||||||
|
Pressure (psig) |
5 lb |
10 lb |
15 lb |
20 lb |
25 lb |
30 lb |
35 lb |
40 lb |
||
|
100 |
338 |
13 |
11.5 |
10.3 |
9.3 |
8.4 |
7.6 |
6.9 |
6.3 |
5.5 |
|
125 |
353 |
14.5 |
13.3 |
11.8 |
10.9 |
10 |
9.2 |
8.5 |
7.9 |
7.2 |
|
150 |
366 |
16 |
14.6 |
13.2 |
12.3 |
11.4 |
10.6 |
9.9 |
9.3 |
8.5 |
|
175 |
377 |
17 |
15.8 |
14.4 |
13.4 |
12.5 |
11.6 |
11.1 |
10.4 |
9.7 |
|
200 |
388 |
18 |
16.9 |
15.5 |
14.6 |
13.7 |
12.9 |
12.2 |
11.6 |
10.9 |
|
225 |
397 |
19 |
17.8 |
16.5 |
15.5 |
14.7 |
13.9 |
13.2 |
12.6 |
11.9 |
|
250 |
406 |
20 |
18.8 |
17.4 |
16.5 |
15.6 |
14.9 |
14.2 |
13.6 |
12.9 |
|
300 |
421 |
21.5 |
20.3 |
19 |
18 |
17.2 |
16.5 |
15.8 |
15.2 |
14.5 |
|
350 |
435 |
23 |
21.8 |
20.5 |
19.5 |
18.7 |
18 |
17.3 |
16.7 |
16 |
|
400 |
448 |
24 |
23 |
21.8 |
21 |
20 |
19.3 |
18.7 |
18.1 |
17.5 |
|
450 |
459 |
25 |
24.3 |
23 |
22 |
21.3 |
20 |
19.9 |
19.3 |
18.7 |
|
500 |
470 |
26.5 |
25.4 |
24.1 |
23.2 |
22.4 |
21.7 |
21.1 |
20.5 |
19.9 |
|
550 |
480 |
27.5 |
26.5 |
25.2 |
24.3 |
23.5 |
22.8 |
22.2 |
21.6 |
20.9 |
|
600 |
488 |
28 |
27.3 |
26 |
25 |
24.3 |
23.6 |
23 |
22.4 |
21.8 |
|
Btu in flash per lb |
1150 |
1155 |
1160 |
1164 |
1167 |
1169 |
1172 |
1174 |
1176 |
|
|
Temp. of liquid, oF |
212 |
225 |
240 |
250 |
259 |
267 |
274 |
280 |
287 |
|
|
Steam volume, cu ft/lb |
26.8 |
21 |
16.3 |
13.7 |
11.9 |
10.5 |
9.4 |
8.5 |
7.8 |
|
Source: Madden Corp. catalog. |
If the steam is saturated, t = tsat. If the steam is wet with a steam quality of x, then the leakage flow is obtained from Eq. (27) divided by „/x. Because the steam is saturated (x = 1),
W = 50 x 3 .14 x ^ x 4 x 100 = 61 lb/h
If the steam were superheated and at 900°F, then
61 = 50 lb/h
1 + 0.00065 x (900 — 544)
544°F is the saturation temperature at 1000 psia. If the steam were wet with a quality of 80%, then
61 = 68 lb/h
How is the discharge flow of air from high pressure to atmospheric pressure determined?
Critical flow conditions for air are found in several industrial applications such as flow through soot blower nozzles, spray guns, and safety valves and leakage through holes in pressure vessels. The expression that relates the variables is [8]
/MW�’5 , N
W = 356 x OP xf — (28)
Where
0 area of opening, in.2
MW molecular weight of air, 28.9 T = absolute temperature, °R P = relief or discharge pressure, psia
What is the leakage air flow from a pressure vessel at 40 psia if the hole is 0.25 in. in diameter? Air is at 60°F.
0.25 2
O = 3.14 x 0.25 x——— = 0.049 in.2
4
Hence,
/28 9 0,5
= 356 x 0.049 x 40 x ( — j = 164 lb/h
Derive an expression for the leakage of gas across a damper, stating the assumptions made.
Most of the dampers used for isolation of gas or air in ducts are not 100% leakproof. They have a certain percentage of leakage area, which causes a flow of
Gas across the area. Considering the conditions to be similar to those of flow across an orifice, we have
![]() (29)
(29)
Where
Vg = gas velocity through the leakage area, fps Hw = differential pressure across the damper, in. WC pg, pw = density of gas and water, lb/cu ft g = acceleration due to gravity, ft/s2 Cd = coefficient of discharge, 0.61
The gas flow W in lb/h can be obtained from
![]() (30)
(30)
Where E is the sealing efficiency on an area basis (%). Most dampers have an E value of 95-99%. This figure is provided by the damper manufacturer. A is the duct cross section, ft2. Substituting Cd = 0.61 and pg = 40/(460 + t) into Eqs. (29) and (30) and simplifying, we have
|
|
(31)
Where t is the gas or air temperature, °F.
A boiler flue gas duct with a diameter of 5 ft has a damper whose sealing efficiency is 99.5%. It operates under a differential pressure of 7 in. WC when closed. Gas temperature is 540°F. Estimate the leakage across the damper. If energy costs $3/MM Btu, what is the hourly heat loss and the cost of leakage?
Substitute O = 3.14 x 52/4, Hw = 7, t = 540, and E = 99.5 into Eq. (31). Then
|
7 VTЦЦЦ |
![]() 52
52
W = 2484 x 3.14 x — x (100 — 99.5) x 2040 lb/h
The hourly heat loss can be obtained from
Q = WCp(t — ta) = 2040 x 0.26 x (540 — 80)
= 240,000 Btu/h = 0 . 24 MM Btu/h
Where Cp is the gas specific heat, Btu/lb °F. Values of 0.25-0.28 can be used for quick estimates, depending on gas temperature. ta is the ambient temperature in °F. 80 ° F was assumed in this case. The cost of this leakage = 0.24 x 3 = $0.72/h.
How is the sealing efficiency of a damper defined?
The sealing efficiency of a damper is defined on the basis oF thE area of cross section of the damper and also as a percentage of flow. The latter method of definition is a function of the actual gas flow condition.
In Q5.20b, the damper had an efficiency of 99.5% on an area basis. Assume that the actual gas flow was 230,000 lb/h. Then, on a flow basis, the efficiency would be
2040
100————— = 99.12%
230.000
If the flow were 115,000 lb/h and the differential pressure were maintained, the efficiency on an area basis would still be 99.5%, whereas on a flow basis it would be
2040
100————— = 98.24%
115.000
Plant engineers should be aware of these two methods of stating the efficiency of dampers.
50,0 lb/h of flue gas flows from a boiler at 800°F. If a waste heat recovery system is added to reduce its temperature to 350°F, how much energy is saved? If energy costs $3/MM Btu and the plant operates for 6000h/year, what is the annual savings? If the cost of the heat recovery system is $115,000, what is the simple payback?
The energy savings Q = WCp(t1 — t2), where tj and t2 are gas temperatures before and after installation of the heat recovery system, °F. Cp is the gas specific heat, Btu/lb °F. Use a value of 0.265 when the gas temperature is in the range of 400-600°F.
Q = 50,000 x 0.265 x (800 — 350) = 5 . 85 x 106 = 5 . 85 MM Btu/h
Annual savings = 5 .85 x 6000 x 3 = $105,000
Hence
Simple payback = 115,000 = ц years, or 13 months F F * 105,000 *
What is life-cycle costing? Two bids are received for a fan as shown below. Which bid is better?
|
Bid 1 |
Bid 2 |
|
|
Flow, acfm |
10,000 |
10,000 |
|
Head, in. WC |
8 |
8 |
|
Efficiency, % |
60 |
75 |
|
Total cost, fan and motor, $ |
17,000 |
21,000 |
Life-cycle costing is a methodology the computes the total cost of owning and operating the equipment over its life. Several financing methods and tax factors would make this a complicated evaluation. However, let us use a simple approach to illustrate the concept. To begin with, the following data should be obtained.
Cost of electricity, Ce = $0.25/kWh Annual period of operation, N = 8000 h Life of equipment, T = 15 years Interest rate, i = 0.13 (13%)
Escalation rate, e = 0.08 (8%)
If the annual cost of operation is Ca, the life-cycle cost (LCC) is LCC = Cc + CaF
Where Cc is the cost of equipment and F is a factor that capitalizes the operating cost over the life of the equipment. It can be shown [4,5] that
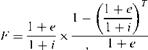
|
1 |
![]()
|
1 + i |
![]() (33)
(33)
|
(34) |
![]() The annual cost of operation is given by
The annual cost of operation is given by
Ca=PCeN where P is the electric power consumed, kW.
|
|
(35)
Hw= head, in. WC Zf = efficiency, fraction q = flow, acfm
Let us use the subscripts 1 and 2 for bids 1 and 2.
8
Pj = 1.17 x 10-4 x 10,000 x = 15.6 kW
0.60
8
P2 = 1.17 x 10-4 x 10,000 x———— = 12.48 kW
2 0:75
From Eq. (33), substituting e = 0.08, i = 0.13, and T = 15, we get F= 10.64. Calculate Ca from Eq. (34):
Ca1 = 15.6 x 8000 x 0.025 = $3120
Ca2 = 12.48 x 8000 x 0.025 = $2500
Using Eq. (32), calculate the life-cycle cost.
LCC1 = 17,000 + 3120 x 10.64 = $50,196
LCC2 = 21,000 + 2500 x 10.64 = $47,600
We note that bid 2 has a lower LCC and thus may be chosen. However, we have to analyze other factors such as period of operation, future cost of energy, and so on, before deciding. If N were lower, it is likely that bid 1 would be better.
Hence, the choice of equipment should not be based only on the initial investment but on an evaluation of the life-cycle cost, especially as the cost of energy is continually increasing.
A process kiln omits 50,000 lb/h of flue gas at 800°F. Two bids were received for heat recovery systems, as follows:
|
Bid 1 |
Bid 2 |
|
|
Gas temperature leaving system, °F |
450 |
300 |
|
Investment, $ |
215,000 |
450,000 |
If the plant operates for 6000 h/year and interest, escalation rates, and life of plant are as in Q5.22, evaluate the two bids if energy costs $4/MM Btu.
Let us calculate the capitalized savings and compare them with the investments. For bid 1:
Energy recovered = 50,000 x 0.25 x (800 — 450)
= 4. 375 MM Btu/h
This energy is worth
4. 375 x 4 = $17 . 5/h
Annual savings = 6000 x 17.5 = $105,000
The capitalization factor from Q5.22 is 10.64. Hence capitalized savings (savings throughout the life of the plant) = 105,000 x 10.64 = $1.12 x 106. A similar calculation for bid 2 shows that the capitalized savings will be $1.6 x 106. The difference in capitalized savings of $0.48 x 106, or $480,000, exceeds the difference in the investment of $235,000. Hence bid 2 is more attractive.
If, however, energy costs $3/MM Btu and the plant works for 2500 h/year, capitalized savings on bid 1 will be $465,000 and that of bid 2 $665,000. The difference of $200,000 is less than the difference in investment of $235,000. Hence under these conditions, bid 1 is better.
The cost of energy and period of operation are important factors in arriving at the best choice.
Determine the thickness of the tubes required for a boiler super-heater. The material is SA 213 T11; the metal temperature is 900°F (see Q8.16a for a
Discussion of metal temperature calculation), and the tube outer diameter is 1.75in. The design pressure is 1000 psig.
Per ASME Boiler and Presswre VfesseZ Code, Sec. 1, 1980, p. 27, the following equation can be used to obtain the thickness or the allowable pressure for tubes. (A tube is specified by the outer diameter and minimum wall thickness, where as a pipe is specified by the nominal diameter and average wall thickness.) Typical pipe and tube materials used in boiler applications are shown in Tables 5.3 And 5.7.
Pd
= 2S + 0.005d + e (36)
P = d-CO1^ — e) (37)
Where
Tw = minimum wall thickness, in.
P = design pressure, psig d = tube outer diameter, in.
E = factor that accounts for compensation in screwed tubes, generally zero Sa = allowable stress, psi
|
Table 5.7 Allowable Stress Values, Ferrous Tubing, 1000 psi
|
|
Source: ASME, Boiler and Pressure Vessel Code, Sec. 1, Power boilers, 1980. |
From Table 5.7, Sa is 13,100. Substituting into Eq. (36) yields 1000 x 1.75
^ = 2 x 13,100+ 1000 + °005 x175 = 0.073in
The tube with the next higher thickness would be chosen. A corrosion allowance, if required, may be added to tw.
Determine the maximum pressure that an SA 53 B carbon steel pipe of size 3 in. schedule 80 can be subjected to at a metal temperature of 550°F. Use a corrosion allowance of 0.02 in.
By the ASME COde, Sec. 1, 1980, p. 27, the formula for determining allowable pressures or thickness of pipes, drums, and headers is
TOC o "1-5" h z Pd, N
Tw =——————— 1- c (38)
W 2SaE + 0 . 8P V 7
where
E = ligament efficiency, 1 for seamless pipes c = corrosion allowance
From Table 5.3, a 3 in. schedule 80 pipe has an outer diameter of 3.5 in. and a nominal wall thickness of 0.3 in. Considering the manufacturing tolerance of 12.5%, the minimum thickness available is 0.875 x 0.3 =0.2625 in.
Substituting Sa = 15,000 psi (Table 5.7) and c = 0 . 02 into Eq. (38), we
Have
3 5P
0.2625 =————————— + 0.02
2 x 15,000 + 0. 8P
Solving for P, we have P = 2200 psig.
For alloy steels, the factor 0.8 in the denominator would be different. The ASME Code may be referred to for details [6]. Table 5.8 gives the maximum allowable pressures for carbon steel pipes up to a temperature of 650°F [7].
How is the maximum allowable external pressure for boiler tubes determined?
|
Nominal pipe size (in.) |
Schedule 40 |
Schedule 80 |
Schedule 160 |
|
1/4 |
4830 |
6833 |
— |
|
1/2 |
3750 |
5235 |
6928 |
|
1 |
2857 |
3947 |
5769 |
|
12 |
2112 |
3000 |
4329 |
|
2 |
1782 |
2575 |
4225 |
|
21 |
1948 |
2702 |
3749 |
|
3 |
1693 |
2394 |
3601 |
|
4 |
1435 |
2074 |
3370 |
|
5 |
1258 |
1857 |
3191 |
|
6 |
1145 |
1796 |
3076 |
|
8 |
1006 |
1587 |
2970 |
|
ABased on allowable stress of 15,000psi; corrosion allowance is zero. Source: Ref. 7. |
A:
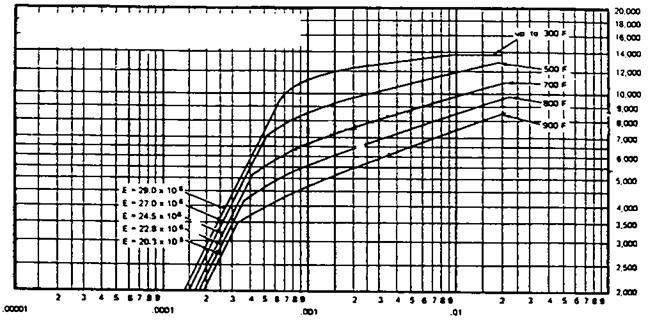
According to ASME Code [9], the external pressures of tubes or pipes can be determined as follows.
For cylinders having do/t > 10,
4B, N
Pa = (39)
3(do/t)
Where
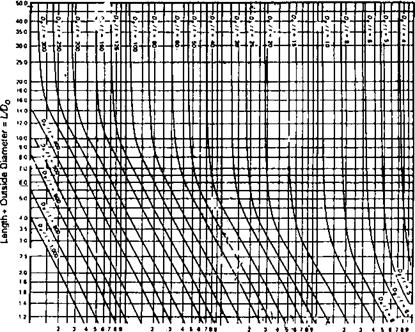
Pa = maximum allowable external pressure, psi A, B = factors obtained from ASME Code, Sec. 1, depending on values of do/t and L/do, where L, do, and t refer to tube length, external diameter, and thickness.
When do/t < 10, A and B are determined from tables or charts as in Q5.25. For do/t < 4, A = 1. 1 /(do/t)2. Two values of allowable pressures are then computed, namely, Pa1 and Pa2.
Pa1 = (lUT — 0 0833 1 ^
And
P —2S x 1 — t/do Pa2 = 2Sb X do/t
Where Sb is the lesser of 2 times the maximum allowable stress values at design metal temperature from the code stress tables or 1.8 times the yield strength of the material at design metal temperature. Then the smaller of the Pa1 or Pa2 is used
For Pa.
Determine the maximum allowable external pressure at 600°F for 120 in. SA 192 tubes of outer diameter 2 in. and length 15 ft used in fire tube boilers.
So/wft’on. do 15 x 12
= 90
TOC o "1-5" h z L 2.0
And
D2
= 16.7
T 0.120
From Fig. 5.3 Factor A = 0.004. From Fig. 5.4, B = 9500. Since do/t > 10,
4B „ 9500 0 .
= —————————— = 4 x = 758 psi
A 3(do/t) 3/16.7 p
What is a decibel? How is it expressed?
The decibel (dB) is the unit of measure used in noise evaluation. It is a ratio (not an absolute value) of a sound level to a reference level and is stated as a sound pressure level (SPL) or a sound power level (PWL). The reference level for SPL is 0.0002 mbar. A human ear can detect from about 20dB to sound pressures
100,0 times higher, 120 dB.
Audible frequencies are divided into octave bands for analysis. The center frequencies in hertz (Hz) of the octave bands are 31.5, 63, 125, 250, 500, 1000, 2000, 4000, and 8000 Hz. The human ear is sensitive to frequencies between 500 and 3000 Hz and less sensitive to very high and low frequencies. At 1000 Hz, for example, 90 dB is louder than it is at 500 Hz.
The sound meter used in noise evaluation has three scales, A, B, and C, which selectively discriminate against low and high frequencies. The A scale (dBA) is the most heavily weighted scale and approximates the human ear’s response to noise (500-6000 Hz). It is used in industry and in regulations regarding the evaluation of noise. Table 5.9 gives typical dBA levels of various
|
Figure 5.3 Factor A for use in external pressure calculation [9]. |
Noise sources, and Table 5.10 Gives the permissible Occupational Safety and Health Act (OSHA) noise exposure values.
How are decibels added? A noise source has the following dB values at center frequencies:
Hz 31.5 63 125 250 500 1000 2000 4000 8000
DB 97 97 95 91 84 82 80 85 85
What is the overall noise level?
|
|
|
FACTOR A |
|
Figure 5.4 Factor B for use in external pressure calculation (SA 178A, SA 192 tubes) [9]. |
|
DBA |
Source |
Perception/hearing |
|
140 |
Jet engine at 25 ft |
Unbearable |
|
130 |
High pressure safety vent at 25 ft |
Threshold of pain |
|
120 |
Large forced draft fan plenum area |
Uncomfortably loud |
|
110 |
8000 hp engine exhaust at 25 ft |
|
|
100 |
Compressor building |
Very loud |
|
90 |
Boiler room |
|
|
80 |
Pneumatic drill |
Loud |
|
70 |
Commercial area |
|
|
60 |
Normal conversation |
|
|
50 |
Average home |
Comfortable |
|
40 |
Nighttime residential area |
|
|
30 |
Broadcast studio |
|
|
20 |
Whisper |
Barely audible |
|
0 |
Threshold of hearing |
A:
Decibels are added logarithmically and not algebraically. 97 dB plus 97 dB is not 194 dB but 100 dB.
P = 10 log(10Pl/1° + 10P2/10 + 10P3/10 + •••)
= 10 log(109 7 + 109 7 + 109 5 + 1091 + 1084 + 108 2 + 108 + 1085 + 1085)
= 102 dB
|
Table 5.10 Permissible Noise Exposures (OSHA)
|
What are SPL and PWL?
SPL is sound pressure level, which is dependent on the distance and environment and is easily measured with a sound level meter. SPL values should be referred to distance. PWL is sound power level and is a measure of the total acoustic power radiated by a given source. It is defined as
PWL = 10log(j^Il)dB (40)
PWL is a constant for a given source and is independent of the environment. It cannot be measured directly but must be calculated. PWL can be roughly described as beinG Equal to the wattage rating of a bulb. Manufacturers of fans and gas turbines publish the values of PWL of their machines. When selecting silencers for these equipment, PWL may be converted to SPL depending on distance, and the attenuation desired at various frequencies may be obtained. A silencer that gives the desired attenuation can then be chosen.
A sound level of 120 dB is measured at a distance of 3 ft from a source. Find the value at 100 ft.
The following formula relates the PWL and SPL with distance:
SPL = PWL — 20 logL + 2.5 dB (41)
Where L = distance, ft.
PWL is a constant for a given source. Hence
SPL + 20 log L = a constant
120 + 20 log 3 = SPL2 + 20 log 100
Hence
SPL2 = 89.5 dB
Thus we see that SPL has decreased by 30 dB with a change from 3 ft to 100 ft. When selecting silencers, one should be aware of the desired SPL at the desired distance. Neglecting the effect of distance can lead to specifying a larger and more costly silencer than necessary.
Q:
How is the noise level from the exhaust of engines computed?
A:
A gas turbine exhaust has the noise spectrum given in Table 5.11 at various octave bands. The exhaust gases flow through a heat recovery boiler into a stack that is 100 ft high. Determine the noise level 150 ft from the top of the stack (of diameter 60 in.) and in front of the boiler.
Assume that the boiler attenuation is 20 dB at all octave bands. In order to arrive at the noise levels at the boiler front, three corrections are required: (1) boiler attenuation, (2) effect of directivity, and (3) divergence at 150 ft. The effect of directivity is shown in Table 5.12. The divergence effect is given by 20 log L — 2.5, where L is the distance from the noise source.
Row 8 values are converted to dBA by adding the dB at various frequencies. The final value is 71 dBA.
5.32
Q:
How is the holdup or volume of water in boiler drums estimated? A boiler generating 10,000 lb/h of steam at 400 psig has a 42 in. drum 10 ft long with 2:1 ellipsoidal ends. Find the time between normal water level (NWL) and low level cutoff (LLCO) if NWL is at 2 in. below drum centerline and LLCO is 4 in. below NWL.
|
Table 5.11 Table of Noise Levels
|
|
—r 71 |
TAble 5.12 Effect of Directivity Based on Angle to Direction of Flow and Size of Silencer Outlet
|
Octave band center frequency (Hz)
|
|
Of flow 0° L°° I /45° |
|
■90“ |
![]()
|
M |
![]()
|
135° |
![]()
|
45° 90 and 135° |

SHAPE \* MERGEFORMAT ![]()
Source: Burgess Manning.
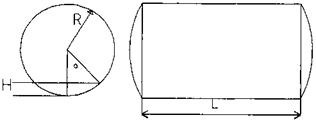
The volume of water in the drum must include the volume due to the straight section plus the dished ends.
Volume in the straight section, is given by
= L x R2 x 1———— sin a x cos a)
S V57.3 /
Where a is the angle shown iN Fig. 5.5. The volume of liquid in each end is given by
V e = 0.261 x H2 x(3R — H)
|
FIgure 5.5 Partial volume of water in boiler drum. |
Where
H = straight length of drum R = drum radius
In this case, H = 120 in. and R = 21 in.
Let us compute Vs1 and Ve1, the volume of the straight section and each end corresponding to the 19 in. level from the bottom of the drum.
Cos a = — = 0.09523 21
Hence
A = 84.5° and sin a = 0.9954
Vs1 = 120 x 21 x 21 x “ 0.0953 x 0.9954
= 73,051 cu in.
Ve1 = 0.261 x 19 x 19 x (3 x 21 — 19) = 4146 cu in.
Hence total volume of liquid up to 19 in. level = 73,051 + 2 x 4146 = 81,343 cu in. = 47.08 cu ft.
Similarly, we can show that total volume of water up to the 15 in. level = 34.1 cu ft. Hence the difference is 13 cu ft.
Specific volume of water at 400psig = 0.0193 cu ft/lb.
0.0193
Normal evaporation rate = 10,000 x ———
60
= 3.2 cu ft/min
Hence the length of time between the levels assuming that the water supply has been discontinued = 13/3.21 = 4.05min.



 11 августа, 2013
11 августа, 2013  doctype
doctype 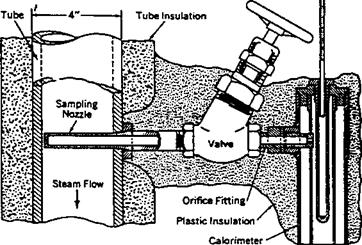
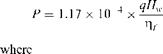
 Опубликовано в рубрике
Опубликовано в рубрике