12 августа, 2013 
doctype 6.1 Estimating HHV (higher heating value) and LHV (lower heating value) of fuels from ultimate analysis; relating heat inputs based on HHV and LHV; relating boiler efficiencies based on HHV and LHV
6.2 Estimating HHV and LHV of fuel oils if °API is known
6.3 Calculating cost of fuels on MM Btu (million Btu) basis; comparing electricity cost with cost of fuels
6.4 Estimating annual fuel cost for power plants; relating heat rates with efficiency of power plants
6.5 Determining gas regulator settings for different fuels
6.6 Correcting fuel flow meter readings for operating fuel gas pressures and temperatures
6.7 Determining energy, steam quantity, and electric heater capacity required for heating air
6.8 Determining energy, steam quantity, and electric heater capacity required for heating fuel oils
6.9 Combustion calculations from ultimate analysis of fuels; determining wet and dry air and flue gas quantities; volumetric analysis of flue gas on wet and dry basis; partial pressures of water vapor and carbon dioxide in flue gas; molecular weight and density of flue gas
6.10 Combustion calculations on MM Btu basis; determining air and flue gas quantities in the absence of fuel data
6.11 Estimating excess air from flue gas CO2 readings
6.12 Estimating excess air from CO2 and O2 readings; estimating excess air
From O2 readings alone
6.13 Effect of reducing oxygen in flue gas; calculating flue gas produced; calculating energy saved and reduction in fuel cost
6.14 Effect of fuel heating values on air and flue gas produced in boilers
6.15 Determining combustion temperature of different fuels in the absence of
Fuel analysis
6.16a Calculating ash concentration in flue gases
6.16b Relating ash concentration between mass and volumetric units
6.17 Determining melting point of ash knowing ash analysis
6.18 Determining SO2 and SO3 in flue gases in lb/MM Btu and in ppm
(volume)
6.19 Determining efficiency of boilers and heaters; efficiency on HHV basis;
Dry gas loss; loss due to moisture and combustion of hydrogen; loss due
To moisture in air; radiation loss; efficiency on LHV basis; wet flue gas loss; relating efficiencies on HHV and LHV basis
6.20 Determining efficiency of boilers and heaters on HHV and LHV basis from flue gas analysis
6.22 Simple formula for efficiency determination
6.23 Determining radiation losses in boilers and heaters if casing temperature and wind velocity are known
6.24 Variation of heat losses and efficiency with boiler load
6.25a Sulfur dew point of flue gases
6.25b Computing acid dew points for various acid vapors
6.25c Effect of gas temperature on corrosion potential
6.25d Another correlation for sulfuric acid dew point
6.26a Converting NOx and CO from lb/h to ppm for turbine exhaust
Gases
6.26b Converting NOx and CO from lb/h to ppm for fired boilers
6.26c Converting UHC from lb/MM Btu to ppm
6.26d Converting SOx from lb/MM Btu to ppm
6.26e Converting NOx and CO from lb/h to ppm before and after auxiliary
Firing in an HRSG
6.26f Relating steam generator emission from measured oxygen value to 3% basis
6.27a Oxygen consumption versus fuel input for gas turbine exhaust gases 6.27b Determining gas turbine exhaust gas analysis after auxiliary firing
6.27c Determining turbine exhaust gas temperature after auxiliary firing
6.28 Relating heat rates of engines to fuel consumption
How are the HHV (higher heating value) and LHV (lower heating value) of fuels estimated when the ultimate analysis is known?
We can use the expressions [1]
HHV = 14,500 x C + 62,000 x ^H2 — O) + 4000 x S (1)
LHV = HHV — 9720 x H2 — 1110 W (2)
Where W is the fraction by weight of moisture in fuel, and C, H2, O2, and S are fractions by weight of carbon, hydrogen, oxygen, and sulfur in the fuel.
If a coal has C = 0.80, H2 = 0.003, O2 = 0.005, W = 0.073, S = 0.006, and the rest ash, find its HHV and LHV. Substituting into Eqs. (1) and (2), we have
, 0.005′
HHV = 14,500 x 0.80 + 62,000 x 0.003 —
8
+ 4000 x 0.006 = 11,771 Btu/lb LHV = 11,771 — 9720 x 0.003 — 1110 x 0.073 = 11,668 Btu/lb
Fuel inputs to furnaces and boilers and efficiencies are often specified without reference to the heating values, whether HHV or LHV, which is misleading.
If a burner has a capacity of Q MM Btu/h (million Btu/h) on HHV basis, its capacity on LHV basis would be
LHV
Qlhv = qhhv x hhv (3a)
Similarly, if ZHHV and ZLHV are the efficiencies of a boiler on HHV and LHV basis, respectively, they are related as follows:
Zhhv x HHV = Zlhv x LHV (3b)
How can we estimate the HHV and LHV of a fuel oil in the absence of its ultimate analysis?
Generally, the °API of a fuel oil will be known, and the following expressions can be used:
TOC o "1-5" h z HHV = 17,887 + 57.5 x °API — 102.2 x %S (4a)
LHV = HHV — 91.23 x %H2 (4b)
Where % H2 is the percent hydrogen by weight.
2122:5
%H = F-°APf+T3L5 (5)
where
F = 24.50 for 0 < °API < 9 F = 25.00 for 9 < °API < 20 F = 25.20 for 20 < °API < 30 F = 25.45 for 30 < °API < 40
HHV and LHV are in Btu/lb.
Determine the HHV and LHV of 30 °API fuel oil in Btu/gal and in Btu/lb. Assume that %S is 0.5.
From Eq. (4a),
HHV = 17,887 + 57.5 x 30 — 102.2 x 0.5 = 19,651 Btu/lb
To calculate the density or specific gravity of fuel oils we can use the expression 141:5 141:5
= 0.876 (6)
131.5 +°API 131.5 + 30
Hence
Density = 0.876 x 8.335 = 7.3 lb/gal 8.335 is the density of liquids in lb/gal when s = 1 HHV in Btu/gal = 19,561 x 7.3 = 142,795
From Eq. (5),
2122 5
%H2 = 25.2———- .———— = 12.05
2 131.5 + 30
LHV = 19,561 — 91.23 x 12.05 = 18,460 Btu/lb
= 18,460 x 7.3 = 134,758 Btu/gal
6.03a Q:
A good way to compare fuel costs is to check their values per MM Btu fired. If coal having HHV = 9500 Btu/lb costs $25/long ton, what is the cost in $/MM Btu?
1 long ton = 2240 lb. 1 MM Btu has 106/9500= 105 lb of coal. Hence 105 lb would cost
105 x -25- = $1.17/MM Btu 2240
If No. 6 fuel oil costs 30 cents/gal, is it cheaper than the coal in Q6.03a?
Table 6.1 gives the HHV of fuel oils. It is 152,400 Btu/gal. Hence 1MM Btu would cost
106
——— x 0.30 = $1.96/MM Btu
152,400
Which is less expensive, electricity at 1.5 cents/kWh or gas at $3/MM Btu?
3413 Btu = 1kWh. At 1.5 cents/kWh, 1MM Btu of electricity costs (106/3413) x 1.5/100 = $4.4. Hence in this case, electricity is costlier than gas. This example serves to illustrate the conversion of units and does not imply that this situation will prevail in all regions.
|
Typical Oil |
°API |
16S cn ° P 6 Tl g 6 P |
Lb/gal |
Kg/m3 |
Gross Btu/gal |
Gross Kcal/L |
Wt% H |
Net Btu/gal |
Net Kcal/L |
Sp. heat at 40° F |
Sp. Heat at 300° F |
Temp. Corr. (°API/°F) |
Air 60° F (ft3/gal) |
Ult. %CO2 |
|
0 |
1.076 |
8.969 |
1,075 |
160,426 |
10,681 |
8.359 |
153,664 |
10,231 |
0.391 |
0.504 |
0.045 |
1581 |
— |
|
|
2 |
1P060 |
8.834 |
1,059 |
159,038 |
10,589 |
8.601 |
152,183 |
10,133 |
0.394 |
0.508 |
— |
— |
— |
|
|
4 |
1.044 |
8.704 |
1,043 |
157,692 |
10,499 |
8.836 |
150,752 |
10,037 |
0.397 |
0.512 |
— |
— |
18.0 |
|
|
6 |
1.029 |
8.577 |
1,0028 |
156,384 |
10,412 |
9.064 |
149,368 |
9,945 |
0.400 |
0.516 |
0.048 |
1529 |
17.6 |
|
|
8 |
1.014 |
8.454 |
1,013 |
155,115 |
10,328 |
9.285 |
148,028 |
9,856 |
0.403 |
0.519 |
0.050 |
1513 |
17.1 |
|
|
10 |
1.000 |
8.335 |
1,000 |
153,881 |
10,246 |
10.00 |
146,351 |
9,744 |
0.406 |
0.523 |
0.051 |
1509 |
16.7 |
|
|
12 |
0.986 |
8.219 |
985.0 |
152,681 |
10,166 |
10.21 |
145,100 |
9,661 |
0.409 |
0.527 |
0.052 |
1494 |
16.4 |
|
|
No. 6 oil |
14 |
0.973 |
8.106 |
971.5 |
151,515 |
10,088 |
10.41 |
143,888 |
9,580 |
0.412 |
0.530 |
0.054 |
1478 |
16.1 |
|
16 |
0.959 |
7.996 |
958.3 |
150,380 |
10,013 |
10.61 |
142,712 |
9,502 |
0.415 |
0.534 |
0.056 |
1463 |
15.8 |
|
|
18 |
0.946 |
7.889 |
945.5 |
149,275 |
9,939 |
10.80 |
141,572 |
9,426 |
0.417 |
0.538 |
0.058 |
1448 |
15.5 |
|
|
No. 5 oil |
20 |
0.934 |
7.785 |
933.0 |
148,200 |
9,867 |
10.99 |
140,466 |
9,353 |
0.420 |
0.541 |
0.060 |
1433 |
15.2 |
|
22 |
0.922 |
7.683 |
920.9 |
147,153 |
9,798 |
11.37 |
139,251 |
9,272 |
0.423 |
0.545 |
0.061 |
1423 |
14.9 |
|
|
24 |
0.910 |
7.585 |
909.9 |
146,132 |
9,730 |
11.55 |
138,210 |
9,202 |
0.426 |
0.548 |
0.063 |
1409 |
14.7 |
|
|
No. 4 oil |
26 |
0.898 |
7.488 |
897.5 |
145,138 |
9,664 |
11.72 |
137,198 |
9,135 |
0.428 |
0.552 |
0.065 |
1395 |
14.5 |
|
28 |
0.887 |
7.394 |
886.2 |
144,168 |
9,599 |
11.89 |
136,214 |
9,069 |
0.431 |
0.555 |
0.067 |
1381 |
14.3 |
|
|
No. 2 oil |
30 |
0.876 |
7.303 |
875.2 |
143,223 |
9,536 |
12.06 |
135,258 |
9,006 |
0.434 |
0.559 |
0.089 |
1368 |
14.0 |
|
32 |
0.865 |
7.213 |
864.5 |
142,300 |
9,475 |
12.47 |
134,163 |
8,933 |
0.436 |
0.562 |
0.072 |
1360 |
13.8 |
|
|
34 |
0.855 |
7.126 |
854.1 |
141,400 |
9,415 |
12.63 |
133,259 |
8,873 |
0.439 |
0.566 |
0.074 |
1347 |
13.6 |
|
|
36 |
0.845 |
7.041 |
843.9 |
140,521 |
9,356 |
12.78 |
132,380 |
8,814 |
0.442 |
0.569 |
0.076 |
1334 |
13.4 |
|
|
38 |
0.835 |
6.958 |
833.9 |
139,664 |
9,299 |
12.93 |
131,524 |
8,757 |
0.444 |
0.572 |
0.079 |
1321 |
13.3 |
|
|
No. 1 oil |
40 |
0.825 |
6.877 |
824.2 |
138,826 |
9,243 |
13.07 |
130,689 |
8,702 |
0.447 |
0.576 |
0.082 |
1309 |
13.1 |
|
42 |
0.816 |
6.798 |
814.7 |
138,007 |
9,189 |
— |
— |
— |
0.450 |
0.579 |
0.085 |
— |
13.0 |
|
|
44 |
0.806 |
6.720 |
805.4 |
137,207 |
9,136 |
— |
— |
— |
0.452 |
0.582 |
0.088 |
— |
12.8 |
Estimate the annual fuel cost for a 300 MW coal-fired power plant if the overall efficiency is 40% and the fuel cost is $1.1 /MM Btu. The plant operates for 6000 h/yr.
Power plants have efficiencies in the range of 35-42%. Another way of expressing this is to use the term heat rate, defined as
3413
Heat rate =————— Btu/kWh
Efficiency
In this case it is 3413/0.4 = 8530 Btu/kWh.
Annual fuel cost = 1000 x megawatt x heat rate x (h/yr) x cost of fuel In $/MM Btu
= 1000 x 300 x 8530 x 6000 x 11
106
= $16.9 x 106
The fuel cost for any other type of power plant could be found in a similar fashion. Heat rates are provided by power plant suppliers.
A 20 MM Btu/h burner was firing natural gas of HHV = 1050Btu/scf with a specific gravity of 0.6. If it is now required to burn propane having HHV = 2300Btu/scf with a specific gravity of 1.5, and if the gas pressure to the burner was set at 4 psig earlier for the same duty, estimate the new gas pressure. Assume that the gas temperature in both cases is 60°F.
The heat input to the burner is specified on HHV basis. The fuel flow rate would be Q/HHV, where Q is the duty in Btu/h. The gas pressure differential between the gas pressure regulator and the furnace is used to overcome the flow resistance according to the equation
KWf2
DP = —f — (7)
P
Where
DP = pressure differential, psi
K = a constant
P = gas density = 0.075s (s is the gas specific gravity; s = 1 for air) Wf = fuel flow rate in lb/h = flow in scfh x 0.075s
Let the subscripts 1 and 2 denote natural gas and propane, respectively.
20 x 106 Wf1 = 1050 x 0.075 x 0.6
20 x 106 Wf2 = 2300 x 0.075 x 1.5
DPj = 4, pj = 0.075 x 0.6, and p2 = 0.075 x 1.5. Hence, from Eq. (7), DPj _ WnP2_ 4 _ 0.6 (2300)2
AP2 W2P1 AP2 (1050)2 1.5
Or
AP2 = 2.08 psig
Hence, if the gas pressure is set at about 2 psig, we can obtain the same duty. The calculation assumes that the backpressure has not changed.
Gas flow measurement using displacement meters indicates actual cubic feet of gas consumed. However, gas is billed, generally, at reference conditions of 60°F and 14.65 psia (4oz). Hence gas flow has to be corrected for actual pressure and temperature. Plant engineers should be aware of this conversion.
In a gas-fired boiler plant, 1000 cu ft of gas per hour was measured, gas conditions being 60 psig and 80°F. If the gas has a higher calorific value of 1050Btu/scf, what is the cost of fuel consumed if energy costs $4/MM Btu?
The fuel consumption at standard conditions is found as follows.
V s = VaPa PT — (8)
PsT a
|
Where |
Vs, Va = fuel consumption, standard and actual, cu ft/h Ts = reference temperature of 520°R Ta = actual temperature, °R Ps, Pa = standard and actual pressures, psia
520
Vs = 100 x (30 + 14.22) x
14.65 x 540 = 2900 scfh
Hence
Energy used = 2900 x 1050 = 3.05 MM Btu/h Cost of fuel = 3.05 x 4 = $12.2/h.
If pressure and temperature corrections are not used, the displacement meter reading can lead to incorrect fuel consumption data.
Estimate the energy in Btu/h and in kilowatts (kW) for heating 75,000 lb/h of air from 90°F to 225°F. What is the steam quantity required if 200psia saturated steam is used to accomplish the duty noted above? What size of electric heater would be used?
The energy required to heat the air can be expressed as
Q = WaCpDT (9)
Where
Q = duty, Btu/h Wa = air flow, lb/h Cp = specific heat of air, Btu/lb°F AT = temperature rise, °F
Cp may be taken as 0.25 for the specified temperature range.
Q = 75,000 x 0.25 x (225 — 90) = 2.53 x 106 Btu/h
Using the conversion factor 3413 Btu = 1 kWh, we have 106
Q = 2.53 x——— = 741 kW
3413
A 750 kW heater or the next higher size could be chosen.
If steam is used, the quantity can be estimated by dividing Q in Btu/h by the latent heat obtained from the steam tables (see the Appendix). At 200 psia, the latent heat is 843 Btu/lb. Hence
106
Steam required = 2.55 x —— = 3046 lb/h
6.08 Q:
Estimate the steam required at 25psig to heat 20gpm of 15 °API fuel oil from 40°F to 180°F. If an electric heater is used, what should be its capacity?
Table 6.2 gives the heat content of fuel oils in Btu/gal [2]. At 180°F, enthalpy is 529 Btu/gal, and at 40°F it is 26 Btu/gal. Hence the energy absorbed by the fuel oil is
Q = 20 x 60 x (529 — 26) = 0.6 x 106 Btu/h 106
= 0.6 x—— = 175 kW 3413
The latent heat of steam (from the steam tables) is 934 Btu/lb at 25psig or 40 psia. Hence
106
Steam required = 0.6 x = 646 lb/h
If an electric heater is used, its capacity will be a minimum of 175 kW Allowing for radiation losses, we may choose a 200 kW heater.
In the absence of information on fuel oil enthalpy, use a specific gravity of
0. 9 and a specific heat of 0.5 Btu/lb °F. Hence the duty will be
0:9
Q = 20 x 60 x 62.40 x — x 0.5 x (180 — 40)
H 7.48 v ’
= 0.63 x 106 Btu/h (7.48 is the conversion factor from cubic feet to gallons.)
|
Gravity, °API at 60°F (15.6°C) |
||||||||
|
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
|
Specific gravity, 60°F/60°F |
||||||||
|
Temp. |
||||||||
|
(°F) |
1.0000 |
0.9659 |
0.9340 |
0.9042 |
0.8762 |
0.8498 |
0.8251 |
0.8017 |
|
32 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
60 |
95 |
93 |
92 |
90 |
89 |
87 |
86 |
85 |
|
965 |
||||||||
|
100 |
237 |
233 |
229 |
226 |
222 |
219 |
215 |
|
|
1065 |
1062 |
|||||||
|
120 |
310 |
305 |
300 |
295 |
290 |
286 |
281 |
|
|
1116 |
1112 |
|||||||
|
140 |
384 |
378 |
371 |
366 |
360 |
355 |
349 |
|
|
1169 |
1164 |
|||||||
|
160 |
460 |
453 |
445 |
438 |
431 |
425 |
418 |
|
|
1236 |
1223 |
1217 |
||||||
|
180 |
538 |
529 |
520 |
511 |
503 |
496 |
488 |
|
|
1293 |
1278 |
1272 |
||||||
|
200 |
617 |
607 |
596 |
587 |
577 |
569 |
560 |
|
|
1371 |
1352 |
1335 |
1327 |
|||||
|
220 |
697 |
686 |
674 |
663 |
652 |
643 |
633 |
|
|
1434 |
1412 |
1393 |
1384 |
|||||
|
240 |
779 |
766 |
753 |
741 |
729 |
718 |
707 |
|
|
1498 |
1474 |
1452 |
1442 |
|||||
|
260 |
862 |
848 |
833 |
820 |
807 |
795 |
783 |
|
|
1563 |
1537 |
1513 |
1502 |
|||||
|
300 |
1034 |
1017 |
999 |
984 |
968 |
954 |
939 |
|
|
1699 |
1668 |
1639 |
1626 |
|||||
|
400 |
1489 |
1463 |
1439 |
1416 |
1393 |
1372 |
1352 |
1333 |
|
2088 |
2064 |
2041 |
2018 |
1997 |
1977 |
1958 |
||
|
500 |
1981 |
1947 |
1914 |
1884 |
1854 |
1826 |
1799 |
1774 |
|
2497 |
2464 |
2434 |
2404 |
2376 |
2349 |
2324 |
||
|
600 |
2511 |
2467 |
2426 |
2387 |
2350 |
2314 |
2281 |
2248 |
|
2942 |
2901 |
2862 |
2825 |
2789 |
2756 |
2723 |
||
|
700 |
3078 |
3025 |
2974 |
2927 |
2881 |
2837 |
2796 |
2756 |
|
3478 |
3425 |
3374 |
3327 |
3281 |
3237 |
3196 |
3156 |
|
|
800 |
3683 |
3619 |
3559 |
3502 |
3447 |
3395 |
3345 |
3297 |
|
4008 |
3944 |
3884 |
3827 |
3772 |
3720 |
3670 |
3622 |
|
AValues in regular type are for liquid; bold values are for vapor. |
|
No. Substance |
Formula |
Mol. Wta |
Lb per Cu ftb |
Cu ft Per lbb |
Spgr air = 1,000b |
Heat of combusionc Btu/cu ft Btu/lb |
|||
|
Gross |
Netd |
Gross |
Netd |
||||||
|
1 Carbon |
C |
12.01 |
— |
— |
— |
— |
— |
14,093g |
14,093 |
|
2 Hydrogen |
H2 |
2.016 |
0.005327 |
187.723 |
0.06959 |
325.0 |
275.0 |
61,100 |
51,623 |
|
3 Oxygen |
O2 |
32.000 |
0.08461 |
11.819 |
1.1053 |
— |
— |
— |
— |
|
4 Nitrogen (atm) |
N2 |
28.016 |
0.07439c |
13.443c |
0.9718e |
— |
— |
— |
— |
|
5 Carbon monxide |
CO |
28.01 |
0.07404 |
13.506 |
0.9672 |
321.8 |
321.8 |
4,347 |
4,347 |
|
6 Carbon dioxide |
CO2 |
44.01 |
0.1170 |
8.548 |
1.5282 |
— |
— |
— |
— |
|
Paraffin series CnH2n+2 |
|||||||||
|
7 Methane |
CH4 |
16.041 |
0.04243 |
23.565 |
0.5543 |
1013.2 |
913.1 |
23,879 |
21,520 |
|
8 Ethane |
C2H6 |
30.067 |
0.08029c |
12.455c |
1.04882e |
1792 |
1641 |
22,320 |
20,432 |
|
9 Propane |
C3H8 |
44.092 |
0.1196c |
8.365c |
1.5617c |
2590 |
2385 |
21,661 |
19,944 |
|
10 n-Butane |
C4H10 |
58.118 |
0.1582c |
6.321c |
2.06654e |
3370 |
3113 |
21,308 |
19,680 |
|
11 Isobutane |
C4H10 |
58.118 |
0.1582e |
6.321e |
2.06654e |
3363 |
3105 |
21,257 |
19,629 |
|
12 n-Pentane |
C5H12 |
72.144 |
0.1904e |
5.252e |
2.4872c |
4016 |
3709 |
21,091 |
19,517 |
|
13 Isopentane |
C5H12 |
72.144 |
0.1904e |
5.252e |
2.4g72e |
4008 |
3716 |
21,052 |
19,47g |
|
14 Neopentane |
C5H12 |
72.144 |
0.1904e |
5.252e |
2.4872e |
3993 |
3693 |
20,970 |
19,396 |
|
15 n-Hexane |
C6H14 |
86.169 |
0.2274e |
4.39ge |
2.9704c |
4762 |
4412 |
20,940 |
19,403 |
|
Olefin series CnH2n |
|||||||||
|
16 Ethylene |
C2H4 |
28.051 |
0.07456 |
13.412 |
0.9740 |
1613.8 |
1513.2 |
21,644 |
20,295 |
|
17 Propylene |
C3H6 |
42.077 |
0.1110e |
9.007e |
1.4504e |
2336 |
2186 |
21,041 |
19,691 |
|
18 n-Butene (butylene) |
C4H8 |
56.102 |
0.1480e |
6.756e |
1.9336e |
3084 |
2gg5 |
20,840 |
19,496 |
|
19 Isobutene |
C4H8 |
56.102 |
0.1480e |
6.756e |
1.9336e |
3068 |
2g69 |
20,730 |
19,382 |
|
20 n-Pentene |
C5H10 |
70.128 |
0.1852e |
5.400e |
2.4190e |
3836 |
3586 |
20,712 |
19,363 |
|
Aromatic series CnH2n_6 |
|||||||||
|
21 Benzene |
C6H6 |
76.107 |
0.2060c |
4.852c |
2.6920e |
3751 |
3601 |
1g,210 |
17,480 |
|
22 Toluene |
C7H8 |
92.132 |
0.2431c |
4.113e |
3.1760e |
4484 |
4284 |
18,440 |
17,620 |
|
23 Xylene |
C8H10 |
106.158 |
0.2803e |
3.567e |
3.6618e |
5230 |
4980 |
18,650 |
17,760 |
|
Miscellaneous gases |
|||||||||
|
24 Acetylene |
C2H2 |
26.036 |
0.06971 |
14.344 |
0.9107 |
1499 |
1448 |
21,500 |
20,776 |
|
25 Naphthalene |
C10H8 |
128.162 |
0.3384e |
2.955e |
4.4208e |
5854f |
5654f |
17,298f |
16,708f |
|
26 Methyl alcohol |
CH3OH |
32.041 |
0.0846e |
11.820e |
1.1052e |
G67.9 |
768.0 |
10,259 |
9,078 |
|
27 Ethyl alcohol |
C2H5OH |
46.067 |
0.1216e |
8.221e |
1.5890e |
1600.3 |
1450.5 |
13,161 |
11,929 |
|
2g Ammonia |
NH3 |
17.031 |
0.0456e |
21.914e |
0.5961e |
441.1 |
365.1 |
9,668 |
8,001 |
|
29 Sulfur |
S |
32.06 |
— |
— |
— |
— |
— |
3,983 |
3,983 |
|
30 Hydrogen sulfide |
H2S |
34.076 |
0.09109e |
10.979e |
1.1g98e |
647 |
596 |
7,100 |
6,545 |
|
31 Sulfur dioxide |
SO2 |
64.06 |
0.1733 |
5.770 |
2.264 |
— |
— |
— |
— |
|
32 Water vapor |
H2O |
18.016 |
0.04758e |
21.017e |
0.6215e |
— |
— |
— |
— |
|
33 Air |
— |
26.9 |
0.07655 |
13.063 |
1.0000 |
— |
— |
— |
— |
All gasvolumes corrected to 60oF and 30 in. Hg dry. Forgases saturated with waterat 60oF, 1.73% ofthe Btuvalue mustbe deducted.
ACalculated from atomic weights given in Journal of the American Chemical Society, February 1937. bDensities calculated from values given in gL at 0oC and 760 mmH in the International Critical Tables allowing for the known deviations from the gas laws. Where the coefficient of expansion was not available, the assumed value was taken as 0.0037 per oC. Compare this with 0.003662, which is the coefficient for a perfect gas. Where no densities were available, the volume of the mole was taken as 22.4115L.
CConverted to mean Btu per lb (1/180 of the heat per lb of water from 32 to 212oF) from data by Frederick D. Rossini, National Bureau of Standards, letter of April 10, 1937, except as noted.
|
Cu ft per cu ft of combustible Lb per lb of combustible —————————————————————————— ———————————————————————————————— Experimental Required for Required for error in Combustion Flue products combustion Flue products heat of ———————————- —————————————— ———————————————— ———————————————- combustion
|
|
2.0 |
7.528 |
9.528 |
1.0 |
2.0 |
7.528 |
3.990 |
13.275 |
17.265 |
2.744 |
2.246 |
13.275 |
0.033 |
|
3.5 |
13.175 |
16.675 |
2.0 |
3.0 |
13.175 |
3.725 |
12.394 |
16.119 |
2.927 |
1.798 |
12.394 |
0.030 |
|
5.0 |
18.821 |
23.821 |
3.0 |
4.0 |
18.821 |
3.629 |
12.074 |
15.703 |
2.994 |
1.634 |
12.074 |
0.023 |
|
6.5 |
24.467 |
30.967 |
4.0 |
5.0 |
24.467 |
3.579 |
11.908 |
15.487 |
3.029 |
1.550 |
11.908 |
0.022 |
|
6.5 |
24.467 |
30.967 |
4.0 |
5.0 |
24.467 |
3.579 |
11.908 |
15.487 |
3.029 |
1.550 |
11.908 |
0.019 |
|
8.0 |
30.114 |
38.114 |
5.0 |
6.0 |
30.114 |
3.548 |
11.805 |
15.353 |
3.050 |
1.498 |
11.805 |
0.025 |
|
8.0 |
30.114 |
38.114 |
5.0 |
6.0 |
30.114 |
3.548 |
11.805 |
15.353 |
3.050 |
1.498 |
11.805 |
0.071 |
|
8.0 |
30.114 |
38.114 |
5.0 |
6.0 |
30.114 |
3.548 |
11.805 |
15.353 |
3.050 |
1.498 |
11.805 |
0.11 |
|
9.5 |
35.760 |
45.260 |
6.0 |
7.0 |
35.760 |
3.528 |
11.738 |
15.266 |
3.064 |
1.464 |
11.738 |
0.05 |
|
3.0 |
11.293 |
14.293 |
2.0 |
2.0 |
11.293 |
3.422 |
11.385 |
14.807 |
3.138 |
1.285 |
11.385 |
0.021 |
|
4.5 |
16.939 |
21.439 |
3.0 |
3.0 |
16.939 |
3.422 |
11.385 |
14.807 |
3.138 |
1.285 |
11.385 |
0.031 |
|
6.0 |
22.585 |
28.585 |
4.0 |
4.0 |
22.585 |
3.422 |
11.385 |
14.807 |
3.138 |
1.285 |
11.385 |
0.031 |
|
6.0 |
22.585 |
28.585 |
4.0 |
4.0 |
22.585 |
3.422 |
11.385 |
14.807 |
3.138 |
1.285 |
11.385 |
0.031 |
|
7.5 |
28.232 |
35.732 |
5.0 |
5.0 |
28.232 |
3.422 |
11.385 |
14.807 |
3.138 |
1.285 |
11.385 |
0.037 |
|
7.5 |
28.232 |
35.732 |
6.0 |
3.0 |
28.232 |
3.073 |
10.224 |
13.297 |
3.381 |
0.692 |
10.224 |
0.12 |
|
9.0 |
33.878 |
32.g78 |
7.0 |
4.0 |
33.878 |
3.126 |
10.401 |
13.527 |
3.344 |
0.782 |
10.401 |
0.21 |
|
10.5 |
39.524 |
50.024 |
8.0 |
5.0 |
39.524 |
3.165 |
10.530 |
13.695 |
3.317 |
0.849 |
10.530 |
0.36 |
|
2.5 |
9.411 |
11.911 |
2.0 |
1.0 |
9.411 |
3.073 |
10.224 |
13.297 |
3.381 |
0.692 |
10.224 |
0.16 |
|
12.0 |
45.170 |
57.170 |
10.0 |
4.0 |
45.170 |
2.996 |
9.968 |
12.964 |
3.434 |
0.562 |
9.968 |
— |
|
1.5 |
5.646 |
7.146 |
1.0 |
2.0 |
5.646 |
1.498 |
4.984 |
6.482 |
1.374 |
1.125 |
4.984 |
0.027 |
|
3.0 |
11.293 |
14.293 |
2.0 |
3.0 |
11.293 |
2.084 |
6.934 |
9.018 |
1.922 |
1.170 |
6.934 |
0.030 |
|
0.75 |
2.823 |
3.573 |
— |
1.5 |
3.323 |
1.409 |
4.688 |
6.097 |
SO2 |
1.587 |
5.511 |
0.088 |
|
SO2 |
0.998 |
3.287 |
4.285 |
1.9928 SO2 |
— |
3.287 |
0.071 |
|||||
|
1.5 |
5.646 |
7.146 |
1.0 |
1.0 |
5.646 |
1.409 |
4.688 |
6.097 |
1.880 |
0.529 |
4.688 |
0.30 |
|
— |
||||||||||||
|
— |
||||||||||||
|
— |
DDeduction from gross to net heating value determined by deducting 18,919 Btu/lb mol water in the products of combustion. Osborne, Stimson and Ginnings, Mechanical Engineering, p. 163, March 1935, and Osborne, Stimson, and Flock, National Bureau of Standards Research Paper 209.
EDenotes that either the density or the coefficient of expansion has been assumed. Some of the materials cannot exist as gases at 60oF and 30in. Hg pressure, in which case the values are theoretical ones given for ease of calculation of gas problems. Under the actual concentrations in which these materials are present their partial pressure is low enough to keep them as gases.
FFrom third edition of Combustion.
Adapted from Ref. 8.
Natural gas having CH4 = 83.4%, C2H6 = 15.8%, and N2 = 0.8% by volume is fired in a boiler. Assuming 15% excess air, 70°F ambient temperature, and 80% relative humidity, perform detailed combustion calculations and determine flue gas analysis.
From Chapter 5 we know that air at 70°F and 80% RH has a moisture content of
0. 012 lb/lb dry air. Table 6.3 can be used to figure air requirements of various fuels. For example, we see that CH4 requires 9.53 mol of air per mole of CH4, and C2H6 requires 16.68 mol.
Let us base our calculations on 100 mol of fuel. The theoretical dry air required will be
83.4 x 9.53 + 16.68 x 15.8 = 1058.3 mol
Considering 15% excess,
Actual dry air = 1.15 x 1058.3 = 1217 mol
Excess air = 0.15 x 1058.3 = 158.7 mol
Excess O2 = 158.7 x 0.21 = 33.3 mol
Excess N2 = 1217 x 0.79 = 961 mol
(Air contains 21% by volume O2, and the rest is N2.)
Moisture in air = 1217 x 29 x 0 = 23.5 mol
18
(We multiplied moles of air by 29 to get its weight, and then the water quantity was divided by 18 to get moles of water.)
Table 6.3 can also be used to get the moles of CO2, H2O, N2 and O2 [3].
CO2 = 1 x 83.4 + 2 x 15.8 = 115 mol H2O = 2 x 83.4 + 3 x 15.8 + 23.5 = 237.7 mol O2 = 33.3 mol N2 = 961 +0.8 = 9618 mol
The total moles of flue gas produced is 115 + 237.7 + 33.3 + 961.8 = 1347.8. Hence
%CO2 = x 100 = 8.5
2 1347.8
Similarly,
%H2O = 17.7, %O2 = 2.5, %N2 = 71.3
%CO2 = 8.5 x——— 100——- = 10.3%
2 100 — 17.7
Similarly,
%O2 = 3.0%, %N2 = 86.7%
To obtain wda, wwa, wdg, and wwg, we need the density of the fUel or the molecular weight, which is
^ x (83.4 x 16 + 15.8 x 30 + 0.8 x 28) = 18.30 29
Wda = 1217 x 100 x 18 3 = 19.29 lb dry air/lb fuel
Wwa = 19 . 29 + j^5^qq = 19 . 52 lb wet air/lb fuel 115 x 44 + 33.3 x 32 + 961 x 28 Wdg = 1830
= 18 lb dry gas/lb fuel
115 x 44 + 33.3 x 32 + 237. 7 x 18 + 961.8 x 28
W =————————————————————————
Wg 1830
= 20 40 lb wet gas/lb fuel
This procedure can be used when the fuel analysis is given. More often, plant engineers will be required to estimate the air needed for combustion without a fuel analysis. In such situations, the MM Btu basis of combustion and calculations will come in handy. This is discussed in Q6.10a.
For the case stated in Q6.09a, estimate the partial pressure of water vapor, pw, and of carbon dioxide, pc, in the flue gas. Also estimate the density of flue gas at 300oF.
The partial pressures of water vapor and carbon dioxide are important in the determination of nonluminous heat transfer coefficients.
Volume of water vapor
Pw =——————————————————- — = 0 .177 atm = 2 . 6 psia
W total flue gas volume
Volume of carbon dioxide
Pc =———- ————————— = 0.085 atm = 1. 27 psia
C total flue gas volume
To estimate the gas density, its molecular weight must be obtained (see Q5.05).
MW ^(MW, x y)
28 x 71.3 + 18 x 17. 7 + 32 x 2. 5 + 44 x 8 . 5 = 100 = 27 7
Hence, from Eq. (6),
14 7
Pg = 27 .7 x 492 x 359 x 76o x,4, 7 = 0 05 lb/cu *
The gas pressure was assumed to be 14.7 psia. In the absence of flue gas analysis, we can obtain the density as discussed in Q5.03.
Pg = 760 = 0 •052 lb/cu ft
Discuss the basis for the million Btu method of combustion calculations.
Each fuel such as natural gas, coal, or oil requires a certain amount of stoichiometric air per MM Btu fired (on HHV basis). This quantity does not vary much with the fuel analysis and has therefore become a valuable method of evaluating combustion air and flue gas quantities produced when fuel gas analysis is not available.
For solid fuels such as coal and oil, the dry stoichiometric air wda in lb/lb fuel can be obtained from
—
|
= 11: 53 x C + 34 • 34 x H |
|
Da |
O) + 4 . 29 x S
Where C, H2, O2, and S are carbon, hydrogen, oxygen, and sulfur in the fuel in fraction by weight.
For gaseous fuels, wda is given by
Wda = 2 . 47 x CO + 34. 34 x H2 + 17 . 27 x CH4 + 13 . 3 x C2H2 + 14 . 81 x C2H4 + 16 .12 x C2H6 — 4 . 32 x O2
Let us compute the amount of air required per MM Btu fired for fuel oil. C = 0.875, H = 0.125, and oAPI = 28.
Solution. From (4a),
HHV = 17,887 + 57.5 x 28 — 102.2 x 0 = 19,497 Btu/lb
The amount of air in lb/lb fuel from the above equation is
Wda = 11.53 x 0.875 + 34.34 x 0.125 = 14.38 lb/lb fuel
1 MM Btu of fuel fired requires (1 x 106)/19,497 = 51.28 lb of fuel. Hence, from the above, 51.28 lb of fuel requires
51.28 x 14.38 = 737 lb of dry air
Table 6.4 shows a range of 735-750. To this must be added excess air; the effect of moisture in the air should also be considered.
Let us take the case of natural gas with the following analysis: methane = 83.4%, ethane = 15.8%, and nitrogen = 0.8%.
Solution. Converting this to percent weight basis, we have
|
Fuel |
% vol |
MW |
Col 2 x col 3 |
% wt |
|
CH4 |
18.3 |
16 |
1334.4 |
72.89 |
|
C2H6 |
15.8 |
30 |
474 |
25.89 |
|
N2 |
0.8 |
28 |
22.4 |
1.22 |
Let us compute the air required in lb/lb fuel.
From Table 6.3,
Air required = 17.265 x 0.7289 + 16.119 x 0.2589 = 16.75 lb/lb fuel
HHV of fuel = 0:7289 x 23,876 + 0:2589 x 22,320 = 23,181 Btu/lb
Where 23,876 and 22,320 are HHV of methane and ethane from Table 6.3.
|
No. |
Fuel |
A |
|
1 |
Blast furnace gas |
575 |
|
2 |
Bagasse |
650 |
|
3 |
Carbon monoxide gas |
670 |
|
4 |
Refinery and oil gas |
720 |
|
5 |
Natural gas |
730 |
|
6 |
Furnace oil and lignite |
745-750 |
|
7 |
Bituminous coals |
760 |
|
8 |
Anthracite |
780 |
|
9 |
Coke |
800 |
The amount of fuel equivalent to 1 MM Btu would be (1 x 106)/ 23,181 = 43.1 lb, which requires 43.1 x 16.75 = 722lb of air, or 1MM Btu fired would need 722 lb of dry air; this is close to the value indicated in Table 6.4.
Let us take the case of 100% methane and see how much air it needs for combustion. From Table 6.3, air required per pound of methane is 17.265 lb, and its heating value is 23,879 Btu/lb. In this case 1MM Btu is equivalent to (1 x 106)/23,879 = 41.88 lb of fuel, which requires 41.88 x 17.265 = 723 lb of dry air.
Taking the case of propane, 1 lb requires 15.703 lb of air.
1 x 106
1 MM Btu =———— = 46 .17 lb fuel
21,661
This would require 46.17 x 15.703 = 725 lb of air.
Thus for all fossil fuels we can come up with a good estimate of theoretical dry air per MM Btu fired on HHV basis, and gas analysis does not affect this value significantly. The amount of air per MM Btu is termed A and is shown in Table 6.4 for various fuels.
A fired heater is firing natural gas at an input of 75 MM Btu/h on HHV basis. Determine the dry combustion air required at 10% excess air and the amount of flue gas produced if the HHV of fuel is 20,000 Btu/lb.
From Table 6.4, A is 730lb/MM Btu. Hence the total air required is Wa = 75 x 1.1 x 730 = 60,200 lb/h
Wg = Wa +Wf = 60,200 + ^0000 = 60’250 lb/h
These values can be converted to volume rates at any temperature using the procedure described in Chapter 5.
The MM Btu method is quite accurate for engineering purposes such as fan selection and sizing of ducts and air and gas systems. Its advantage is that fuel analysis need not be known, which is generally the case in power and process plants. The efficiency of heaters and boilers can also be estimated using the MM Btu method of combustion calculations.
A coal-fired boiler is firing coal of HHV = 9500 Btu/lb at 25% excess air. If ambient conditions are 80°F, relative humidity 80%, and flue gas temperature 300°F, estimate the combustion air in lb/lb fuel, the volume of combustion air in cu ft/lb fuel, the flue gas produced in lb/lb fuel, and the flue gas volume in cu ft/lb fuel.
Because the fuel analysis is not known, let us use the MM Btu method. From Table 6.4, A = 760 for coal. 1 MM Btu requires 760 x 1.25 = 950 lb of dry air. At 80% humidity and 80°F, air contains 0.018 lb of moisture per pound of air (Chap. 5). Hence the wet air required per MM Btu fired is 950 x 1.018 lb. Also,
1 MM Btu fired equals 106/9500 = 105 lb of coal. Hence
950
Wda = dry air, lb/lb fuel = = 9.05
Wwa = wet air, lb/lb fuel = 950 x 1 018 = 9.21 wa ‘ 105
492
Pa = density of air at 80°F = 29 x ^ x 540
= 0.0736 lb/cu ft (see Chap. 5, Q5.03).
Hence
9:21
Volume of air = = 125 cu ft/lb fuel
|
40 760 950 + 105 105 10.05 |
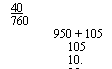0:0736
Pg = density of flue gas = ^^ = 0.0526 lb/cu ft wdg = dry flue gas in lb/lb fuel = — = 10.05
Volume of flue gas, cu ft/lb fuel =———— = 191
0:0526
Is there a way to figure the excess air from flue gas CO2 readings?
Yes. A good estimate of excess air E in percent can be obtained from the equation
E=100 x (%Co ■ 0 <10a)
%CO2 is the percent of carbon dioxide in dry flue gas by volume, and K1 is a constant depending on the type of fuel, as seen in Table 6.5. For example, if %CO2 = 15 in flue gas in a coal-fired boiler, then for bituminous coal (Ki = 18.6),
E = 100 x ^^86 _ l) = 24%
Discuss the significance of %CO2 and %O2 in flue gases.
Excess air levels in flue gas can be estimated if the %CO2 and %O2 in dry flue gas by volume are known. The higher the excess air, the greater the flue gas quantity and the greater the losses. Plant engineers should control excess air levels to help control plant operating costs. The cost of operation with high excess air is discussed in Q6.13.
A formula that is widely used to figure the excess air is [1]
E = 100 x————- °2 ~ CO/2—————- ~ <10b)
0 .264 x N2 — <O2 — CO/2) v ’
|
Table 6.5 K Factors for Fuels
|
|
Source: Ref. 1. |
Where O2, CO, and N2 are the oxygen, carbon monoxide, and nitrogen in dry flue gas, vol%, and E is the excess air, %.
Another formula that is quite accurate is [1]
O2
E = K2 x——— 2— (10c)
2 21 — O2 V 7
Where K2 is a constant that depends on the type of fuel (see Table 6.6).
In a natural gas boiler ofcapacity 50 MM Btu/h (HHV basis), the oxygen level in the flue gas is reduced from 3.0% to 2.0%. What is the annual savings in operating costs if fuel costs $4/MM Btu? The HHV of the fuel is 19,000 Btu/lb. The exit gAs temperature is 500°F, and the ambient temperature is 80°F.
The original excess air is 90 x 3/(21 — 3)= 15% (see Q6.12). The excess air is now
2:0
E = 90 x —:— = 9.47%
21 — 2
With 15% excess, the approximate air required (see Q6.10a) is 50 x 746 x
1.15= 42,895 lb/h.
106
Flue gas = 42,895 + 50 x 19 000 = 45,256 lb/h
|
Table 6.6 Constant k2 Used in Eq. (10c)
|
|
Source: Ref. 1. |
Air required = 50 x 746 x 1.0947 = 40,832 lb/h
106
Flue gas produced = 40,832 + 50 x 19 000 = 43,463 lb/h
Reduction in heat loss = <45,526 — 43,463) x 0.25 x <500 — 80)
= 0 . 22 MM Btu/h
Fuels are often interchanged in boiler plants because of relative availability and economics. It is desirable, then, to analyze the effect on the performance of the system. Discuss the implications of burning coal of 9800 Btu/lb in a boiler originally intended for 11,400 Btu/lb coal.
Let us assume that the duty does not change and that the efficiency of the unit is not altered. However, the fuel quantity will change. Combustion air required, being a function of MM Btu fired, will not change, but the flue gas produced will increase. Let us prepare a table.
|
Coal 1 |
Coal 2 |
|
|
Fuel HHV, Btu/lb |
11,400 |
9800 |
|
Fuel fired per MM Btu (106/HHV) |
87 |
102 |
|
Air required per MM Btu (25% excess air) |
760 x 1.25 = 950 |
760 x 1.25 = 950 |
|
Flue gas, lb |
1037 |
1052 |
|
Ratio of flue gas |
1 |
1.015 |
We can use the same fans, because the variation in flue gas produced is not significant enough to warrant higher gas pressure drops. We must look into other
Aspects, such as the necessity of higher combustion air temperature (due to higher moisture in the fuel), ash concentration, and fouling characteristics of the new fuel. If a different type of fuel is going to be used, say oil, this will be a major change, and the fuel-handling system’s burners and furnace design will have to be reviewed. The gas temperature profiles will change owing to radiation characteristics, and absorption of surfaces such as superheaters and economizers will be affected. A discussion with the boiler design engineers will help.
Q:
What is meant by combustion temperature of fuels? How is it estimated?
A:
The adiabatic combustion temperature is the maximum temperature that can be attained by the products of combustion of fuel and air. However, because of dissociation and radiation losses, this maximum is never attained. Estimation of temperature after dissociation requires solving several equations. For purposes of estimation, we may decrease the adiabatic combustion temperature by 3-5% to obtain the actual combustion temperature.
From an energy balance it can be shown that
LHV + Aa x HHV x Cpa x (ta — 80)/106 tc = (1 — % ash/100 + Aa x HHV/106) x Cpg (11)
Where
LHV, HHV = lower and higher calorific value of fuel, Btu/lb A = theoretical air required per million Btu fired, lb a = excess air factor =1 + E/100 ta, tc = temperature of air and combustion temperature, °F Cpa, Cpg = specific heats of air and products of combustion, Btu/lb °F
For example, for fuel oil with combustion air at 300°F, LHV= 17,000Btu/ lb, HHV = 18,000 Btu/lb, a = 1.15, and A = 745 (see Table 6.4). We have
17,0 + 745 x 1.15 x 18,000 x 0.25 x (300 — 80)/106 tc = (1 + 745 x 1.15 x 18,000/106) x 0.32
= 3400°F
Cpa and Cpg were taken as 0.25 and 0.32, respectively.
How is the ash concentration in flue gases estimated?
Particulate emission data are needed to size dust collectors for coal-fired boilers. In coal-fired boilers, about 75% of the ash is carried away by the flue gases and 25% drops into the ash pit. The following expression may be derived using the MM Btu method of combustion calculation [5]:
240,0 x<% ash/100) a = T x [7 . 6 x 10—6 x HHV x <100 + E) + 1 — <% ash/100)] < a)
Where
Ca = ash concentration, grains/cu ft E = excess air, %
T = gas temperature, °R HHV = higher heating value, Btu/lb
If coals of HHV = 11,000 Btu/lb having 11% ash are fired in a boiler with 25% excess air and the flue gas temperature is 850°R, determine the ash concentration.
Solution. Substituting into Eq. (12a), we have C 240,000 x 0.11
A = 850 x <7.6 x 10—6 x 11,000 x 125 + 1 — 0.11) = 2 75 grains/cu ft
How do you convert the ash concentration in the flue gas in wt% to grains/acf or grains/scf?
Flue gases from incineration plants or solid fuel boilers contain dust or ash, and often these components are expressed in mass units such as lb/h or wt%, whereas engineers involved in selection of pollution control equipment prefer to work in terms of grains/acf or grains/scf (actual and standard cubic feet). The relationship is
Ca = 0 . 01 x A x 7000 x p = 70A <12b)
Where
P = gas density, lb/cu ft = 39.5/(460 + t) t = gas temperature, °F Ca = ash content, grains/acf or grains/scf depending on whether density is computed at actual temperature or at 60°F A = ash content, wt%
The expression for density is based on atmospheric flue gases having a molecular weight of 28.8 (see Q5.03).
Flue gases contain 1.5 wt% ash. The concentration in grains/acf at 400°F is
39:5
Ca = 70 x 1.5 x —— = 4.8 grains/acf
39.5
Ca = 70 x 1.5 x -520 = 7.98 grains/scf
Discuss the importance of the melting point of ash in coal-fired boilers. How is it estimated?
In the design of steam generators and ash removal systems, the ash fusion temperature is considered an important variable. Low ash fusion temperature may cause slagging and result in deposition of molten ash on surfaces such as superheaters and furnaces. The furnace will then absorb less energy, leading to higher furnace exit gas temperatures and overheating of superheaters.
A quick estimate of ash melting temperature in °C can be made using the expression [6]
Tm = 19 x AI2O3 + 15 x (SiO2 + TiO2)
+ 10 x (CaO + MgO)
+ 6 x (Fe2O3 + Na2O + K2O)
Where tm is the fusion temperature in °C, and the rest of the terms are percent ash content of oxides of aluminum, silicon, titanium, calcium, magnesium, iron, sodium, and potassium.
Analysis of a given ash indicates the following composition:
Al2O3 = 20%, SiO2 + TiO2 = 30%
Fe2O3 + Na2O + K2O = 20%, CaO + MgO = 15%
Find the fusion temperature.
Solution. Substituting into Eq. (13), we find that tm = 1100°C.
6.18a Q:
What is the emission of SO2 in lb/MM Btu if coals of HHV = 11,000 Btu/lb and having 1.5% sulfur are fired in a boiler?
The following expression gives e, the emission of SO2 in lb/MM Btu:
S
E = 2 x 104HHV (14)
Where S is the percent sulfur in the fuel.
E = 2 x 104 x 1: 5 = 2.73 lb/MM Btu
11,0 ‘
If an SO2 scrubbing system of 75% efficiency is installed, the exiting SO2 concentration will be 0.25 x 2.73 = 0.68 lb/MM Btu.
What is the SO2 level in ppm (parts per million) by volume if the coals in Q6.18a are fired with 25% excess air?
We have to estimate the flue gas produced. Using the MM Btu method,
106
Wg = + 1.25 x 760 = 1041 lb/MM Btu
G 11,000 ‘
Let the molecular weight be 30, which is a good estimate in the absence of flue gas analysis. Then,
1041
Moles of flue gas = 30 = 34 . 7 per MM Btu fired
2 73
Moles of SO2 =
2 64
= 0.042 (from Q6.18a and Table 5.1)
(64 is the molecular weight of SO2. Dividing weight by molecular weight gives the moles.)
Hence ppm of SO2 in flue gas will be 0.042 x 106/34.7 = 1230 ppm.
If 5% of the SO2 gets converted to SO3, estimate the ppm of SO3 in the flue gas. A:
2 73
Moles of SO3 = 0.05 x—— = 0.0017 per MM Btu 80
Hence
Ppm by volume of SO3 = x
106 = 49 ppm
(80 is the molecular weight of SO3.)
How is the efficiency of a boiler or a fired heater determined?
The estimation of the efficiency of a boiler or heater involves computation of several losses such as those due to flue gases leaving the unit, unburned fuel, radiation losses, heat loss due to molten ash, and so on. Readers may refer to the ASME Power Test Code [7] for details. Two methods are widely used, one based on the measurement of input and output and the other based on heat losses. The latter is preferred, because it is easy to use.
There are two ways of stating the efficiency, one based on HHV and the other on LHV. As discussed in Q6.01,
ZHHV x HHV = ZLHV x LHV
The various losses are [1], on an HHV basis,
1. Dry gas loss, Lj:
L1 = 24wdg ^H-V (15a)
2. Loss due to combustion of hydrogen and moisture in fuel, L2:
L2 =(9 x H2 + W) x (1080 + 0.46tg — ta)
100 x HHV
3. Loss due to moisture in air, L3:
L3 = 46 Mwda (15c)
4. Radiation loss, L4. The American Boiler Manufacturers Association
(ABMA) chart [7] may be referred to to obtain this value. A quick
Estimate of L4 is
L4 = 10062-042 log Q (15d)
For Eqs. (15a)-(15d),
Wdg = dry flue gas produced, lb/lb fuel
Wda = dry air required, lb/lb fuel
H2, W = hydrogen and moisture in fuel, fraction
M = moisture in air, lb/lb dry air (see Q5.09b)
Tg, ta = temperatures of flue gas and air, °F
Qg =aduty in MM Btu/h
5. To losses L1-L4 must be added a margin or unaccounted loss, L5.
Hence efficiency becomes
ZHHV = 100 — (L1 + L2 + L3 + L4 + L5) (15e)
Note that combustion calculations are a prerequisite to efficiency determination.
If the fuel analysis is not available, plant engineers can use the MM Btu method
To estimate wdg rather easily and then estimate the efficiency (see Q6.20).
The efficiency can also be estimated on LHV basis. The various losses considered are the following.
Wwg Cp’^a (15f)
|
1. Wet flue gas loss: tg— HHV |
(Cp, gas specific heat, will be in the range of 0.26-0.27 for wet flue gases.)
2. Radiation loss (see Q6.23)
3. Unaccounted loss, margin
Then
ZLHV =100 — (sum of the above three losses)
One can also convert ZHHV to ZLHV using Eq. (3b) (see Q6.01).
Coals of HHV = 13,500 Btu/lb and LHV= 12,600Btu/lb are fired in a boiler with 25% excess air. If the exit gas temperature is 300°F and ambient temperature is 80°F, determine the efficiency on HHV basis and on LHV basis.
From the MM Btu method of combustion calculations, assuming that moisture in air is 0.013 lb/lb dry air,
1.13 x 760 x 1.25 + 106/13,500
W =■ ————————————————
Wg 106/13,500
= ^ =14 . 0
74
(760 is the constant obtained from Table 6.4.) Hence
Wet flue gas loss = 100 x 14 . 0 x 0 . 26 300 — 80 x 12,600 = 6 . 35%
Let radiation and unaccounted losses be 1.3%. Then ZLHV = 100 — (6.35 + 1.3) = 92.34%
ZHHV = 92.34 x 12,600 = 86.18% lHHV 13,500
(Radiation losses vary from 0.5% to 1.0% in large boilers and may go up to 2.0% in smaller units. The major loss is the flue gas loss.)
Determine the efficiency of a boiler firing the fuel given in Q6.09a at 15% excess air. Assume radiation loss = 1%, exit gas temperature = 400°F, and ambient temperature = 70°F. Excess air and relative humidity are the same as in Q6.09a (15% and 80%).
Results of combustion calculations are already available.
Dry flue gas = 18 lb/lb fuel
Moisture in air = 19:52 — 19:29 = 0:23 lb/lb fuel
Water vapor formed due to combustion of fuel =
20.4 — 18 — 0.23 = 2.17 lb/lb fuel
TTTT, r 83.4 x 1013.2 + 15.8 x 1792 ^
HHV =—————————————— = 1128 Btu/cu ft
100 ‘
Fuel density at 60°F = 18.3/379 = 0.483 lb/cu ft, so 1128
HHV = 00483 = 23,364 Btu/lb The losses are
1. Dry gas loss,
400 — 70
L, = 100 x 18 x 0.24 x—————- = 6.1%
1 23,364
2. Loss due to combustion of hydrogen and moisture in fuel,
1080 + 0.46 x 400 — 70 L2 = 100 x 2.17 x ——
2 23,364
= 11.1%
3. Loss due to moisture in air,
400 — 70
L3 = 100 x 0.23 x 0.46 x _ = 0.15%
3 23,364
4. Radiation loss = 1.0%
5. Unaccounted losses and margin = 0%
Total losses = 6.1 + 11.1 + 0.15 + 1.0 = 18.35%
Hence
Efficiency on HHV basis = 100 — 18.35 = 81.65%
One can convert this to LHV basis after computing the LHV.
How do excess air and boiler exit gas temperature affect the various losses and boiler efficiency?
Table 6.7 shows the results of combustion calculations for various fuels at different excess air levels and boiler exit gas temperatures. It also shows the amount of CO2 generated per MM Btu fired.
It can be seen that natural gas generates the lowest amount of CO2.
106 9.06 x 44
CO2/MMBtu, natural, gas = 23789 x 19.17 x 27 57 x 1oo = n6.5 lb
|
Table 6.7 Combustion Calculations for Various Fuels
Coal (wt%): C = 72.8, H2 = 4.8, N2 = 1.5, O2 = 6.2, S = 2.2, H2O = 3.5, ash = 9.0; HHV = 13139 Btu/lb; LHV = 12,634 Btu/lb. Oil (wt%): C = 87.5, H2 = 12.5, °API = 32; HHV = 19,727 Btu/lb; LHV = 18,512 Btu/lb. Gas (vol%): CH4 = 97; C2H6 = 2, C3H8 = 1; HHV = 23,789 Btu/lb; LHV = 21,462 Btu/lb. |
(The above is obtained by converting the volumetric analysis to weight basis using the molecular weights of CO2 and the flue gas.) For oil, CO2 generated = 162.4 lb, and for coal, 202.9 lb.
6.20 Q:
A fired heater of duty 100MM Btu/h (HHV basis) firing No. 6 oil shows the following dry flue gas analysis:
CO2 = 13. 5%, O2 = 2 . 5%, N2 = 84%
The exit gas temperature and ambient temperature are 300°F and 80°F, respectively. If moisture in air is 0.013 lb/lb dry air, estimate the efficiency of the unit on LHV and HHV basis. LHV = 18,400Btu/lb and HHV = 19,500 Btu/lb.
Because the fuel analysis is not known, let us estimate the flue gas produced by the MM Btu method. First, compute the excess air, which is
E = 94 . 5 x —25— = 12 . 8%
21 -2 . 5
The factor 94.5 is from Table 6.6 (see Q6.12). The wet flue gas produced is
745 x 1.128 x 1.013 106
106 + 19,500
106/19,500 = 17 . 6 lb/lb fuel
Hence
Wet gas loss = 100 x 17.6 x 0.26 x 300—— = 5 . 47%
5 18,400
The radiation loss on HHV basis can be approximated by Eq. (15d):
Radiation loss = 10°’62-0’42 logQ = 0 . 60%
Q = 100 MM Btu/h
Let us use 1.0% on LHV basis, although this may be a bit high. Hence the efficiency on LHV basis is 100 — 6.47 = 93.53%. The efficiency on HHV basis would be [Eq. (3b)]
ZHHV x HHV = ZLHV x LHV
Or
18,400
Zhhv = 95 . 53 x———— = 88 .25
IHHV 19,500
Thus, even in the absence of fuel ultimate analysis, the plant personnel can check the efficiency of boilers and heaters based on operating data.
6.21 Q:
How is the loss due to incomplete combustion such as the formation of CO determined?
Efforts must be made by the boiler and burner designers to ensure that complete combustion takes place in the furnace. However, because of various factors such as size of fuel particles, turbulence, and availability of air to fuel and the mixing process, some carbon monoxide will be formed, which means losses. If CO is formed from carbon instead of CO2, 10,600 Btu/lb is lost. This is the difference between the heat of reaction of the two processes
C + O2 ! CO2 and C + O2 ! CO
The loss in Btu/lb is given by [1]
CO
L = CO+CO x 10,160 x C
Where C is the carbon in the fuel, fraction by weight, and CO and CO2 are vol% of the gases.
Determine the losses due to formation of CO if coal with HHV of 12,000 Btu/lb is fired in a boiler, given that CO and CO2 in the flue gas are 1.5% and 17% and the fuel has a carbon content of 56%.
Solution. Substituting into the equation given above,
1.5 0.56
L =——- x 10,160 x———— = 0.038
18 . 5 12,000
Or L = 3.8% on HHV basis (dividing loss in Btu/lb by HHV).
Is there a simple formula to estimate the efficiency of boilers and heaters if the excess air and exit gas temperature are known and the fuel analysis is not available?
Boiler efficiency depends mainly on excess air and the difference between the flue gas exit temperature and the ambient temperature. The following expressions have been derived from combustion calculations for typical natural gas and oil fuels. These may be used for quick estimations.
For natural gas:
ZHHV, % = 89.4 — (0.001123 + 0.0195 x EA) x AT (16a)
ZLHV, % = 99.0 — (0.001244 + 0.0216 x EA) x AT (16b)
For fuel oils:
ZHHV, % = 92.9 — (0.001298 + 0.01905 x EA) x AT
ZLHV, % = 99.0 — (0.001383 + 0.0203 x EA) x AT
Where
EA = excess air factor (EA = 1.15 means 15% excess air)
AT = difference between exit gas and ambient temperatures Example
Natural gas at 15% excess air is fired in a boiler, with exit gas temperature 280°F and ambient temperature 80°F Determine the boiler efficiency. EA = 1.15 and AT = 280 — 80 = 200°F.
Solution.
ZHHV = 89.4 — (0.001123 + 0.0195 x 1.15) x (280 — 80) = 84.64%
ZLHV = 99.0 — (0.001244 + 0.0216 x 1.15) x (280 — 80) = 93.78%
The above equations are based on 1% radiation plus unaccounted losses.
The average surface temperature of the aluminum casing of a gas-fired boiler was measured to be 180°F when the ambient temperature was 85°F and the wind velocity was 5 mph. The boiler was firing 50,000 scfh of natural gas with LHV = 1075Btu/scf. Determine the radiation loss on LHV basis if the total
Surface area of the boiler was 2500 ft2. Assume that the emissivity of the
Casing = 0.1.
This example shows how radiation loss can be obtained from the measurement of casing temperatures. The wind velocity is 5mph = 440 fpm. From Q8.51 we see that the heat loss q in Btu/ft2 h will be
Q = 0 .173 x 10-8 x 0 .1 x [(460 + 180)4 — (460 + 85)4]
+ 0.296 x (180 — 85)1’25 x 744° + 69 (17)
69
= 252 Btu/ft2 h
The total heat loss will be 2500 x 252 = 0.63 x 106 Btu/h. The radiation loss on LHV basis will be 0.63 x 106 x 100/(50,000 x 1075) = 1.17%. If the HHV of the fuel were 1182Btu/scf, the radiation loss on HHV basis would be 0.63 x 1182/1075 = 1.06%.
How does the radiation loss vary with boiler duty or load? How does this affect the boiler efficiency?
The heat losses from the surface of a boiler will be nearly the same at all loads if the ambient temperature and wind velocity are the same. Variations in heat losses can occur owing to differences in the gas temperature profile in the boiler, which varies with load. However, for practical purposes this variation can be considered minor. Hence the heat loss as a percent will increase as the boiler duty decreases.
The boiler exit gas temperature decreases with a decrease in load or duty and contributes to some improvement in efficiency, which is offset by the increase in radiation losses. Hence there will be a slight increase in efficiency as the load increases, and after a certain load, efficiency decreases.
The above discussion pertains to fired water tube or fire tube boilers and not waste heat boilers, which have to be analyzed for each load because the gas flow
And inlet gas temperature can vary significantly with load depending on the type of process or application.
6.25a Q:
Discuss the importance of dew point corrosion in boilers and heaters fired with fuels containing sulfur.
During the process of combustion, sulfur in fuels such as coal, oil, and gas is converted to sulfur dioxide. Some portion of it (1-5%) is converted to sulfur trioxide, which can combine with water vapor in the flue gas to form gaseous sulfuric acid. If the surface in contact with the gas is cooler than the acid dew point, sulfuric acid can condense on it, causing corrosion. ADP (acid dew point) Is dependent on several factors, such as excess air, percent sulfur in fuel, percent conversion of SO2 to SO3, and partial pressure of water vapor in the flue gas.
Manufacturers of economizers and air heaters suggest minimum cold-end
Temperatures that are required to avoid corrosion. Figures 6.1 and 6.2 are typical. Sometimes the minimum fluid temperature, which affects the tube metal temperature, is suggested. The following equation gives a conservative estimate of the acid dew point [8]:
Tdp = 1.7842 + 0.0269 log pw — 0.129 log^so, , N
(18a)
+ 0.329 log pw x log pso3
Where
Tdp = acid dew point, K pw = partial pressure of water vapor, atm pSO^ = partial pressure of sulfur trioxide, atm
Table 6.8 Gives typical pSO values for various fuels and excess air. Q6.18c shows how ppm SO3 can be computed from which ^SO is obtained.
A practical way to determine Tdp is to use a dew point meter. An estimation of the cold-end metal temperature can give an indication of possible corrosion.
How is the dew point of an acid gas computed?
Table 6.9 shows the dew point correlations for various acid gases [9,11].
|
100 120 140 160 Acid Dew Point Temperature (ADT°CI FIGURE 6.1 The relationship between SO3 and ADT. (Courtesy of Land Combustion Inc.) |
Flue gas from an incinerator has the following analysis (vol%): H2O = 12, SO2 = 0.02, HCl = 0.0015 and the rest oxygen and nitrogen. Gas pressure = 10 in. wg. Compute the dew points of sulfuric and hydrochloric acids given that 2% of SO2 converts to SO3. In order to use the correlations, the gas pressures must be converted to mmHg. Atmospheric pressure = 10 in. wg = 10/407 = 0.02457 atmg or 1.02457 atm abs.
PHiO = 0.12 x 1.02457 x 760 = 93.44 mmHg
Ln Ph2o = 4.537
PHCl = 0.0015 x 1.0245 x 760 = 0.1168 mmHg
Ln. pHCl = —2.1473 Partial pressures of sulfuric acid and SO3 are equal. Hence PSO = 0.02 x 0.0002 x 760 x 1.0245 = 0.0031 mmHg ln PSO3 =-5.7716 Substituting into the equations, we obtain the following.
|
FIGURE 6.2 Limiting tube metal temperatures to avoid external corrosion in economizers and air heaters when burning fuels containing sulfur. (From Ref. 13, with permission.) |
For hydrochloric acid: 1000
= 3.7368 — 0.1591 x 4.537 + 0.0326 x 2.1473
* dp
— 0.00269 x 4.537 x 2.1473 = 3.0588
Or
Tdp = 327 K = 54°C = 129°F
|
Table 6.8 SO3 in Flue Gas (ppm)
|
Hydrobromic acid
1000/Tdp = 3.5639 — 0.1350 In PH2O — 0.0398 In PHBr + 0.00235 In PHjO In PHBr
Hydrochloric acid
1000/Tdp = 3.7368 — 0.1591 In PH2O — 0.0326 In PHCI
+ 0.00269 In Ph2o In PHCI
Nitric acid
1000/Tdp = 3.6614 — 0.1446 In PH2O — 0.0827 In PHNOa
+ 0.00756 In Ph2o In PHNO3
SuIfurous acid
1000/TDp = 3.9526 — 0.1863 In PHaO + 0.000867 In PSO2
— 0.000913 In Ph2o In PSO2
SuIfuric acid
1000/Tdp = 2.276 — 0.0294 In PH2O — 0.0858 In PHaSO4
+ 0.0062 In Ph2o In PH2SO4
ATdp is dew point temperature (K), and P is partiaI pressure (mmHg). Compared with pubIished data, the predicted dew points are within about 6 K of actuaI vaIues except for H2SO4, which is within about 9 K. Source: HCI, HBr, HNO3 and SO2 correIations were derived from vapor-Iiquid equiIibrium data. The H2SO4 correIation is from Ref. 5.
For sulfuric acid:
1000
|
Tdp |
■ = 2.276 — 0.0294 x 4.537 + 0.0858 x 5.7716
— 0.0062 x 4.537 x 5.7716 = 2.4755
Or
Tdp = 404 K = 131°C = 268°F The dew points of other gases can be obtained in a similar manner.
6.25c
Q:
Does the potential for acid dew point corrosion decrease if the gas temperature at the economizer is increased?
Acid dew points were computed in Q6.25a. If the tube wall temperatures can be maintained above the dew point, then condensation of vapors is unlikely. However, the tube wall temperature in a gas-to-liquid heat exchanger such as the economizer is governed by the gas film heat transfer coefficient rather than the tube-side water coefficient, which is very high.
It can be shown by using the electrical analogy and neglecting the effects of fouling that [9]
Tm = t0 — ( — ti) j—ho
Where
Tm = tube wall temperature t0 = gas — and tube-side fluid temperature ht = tube-side heat transfer coefficient h0 = gas-side heat transfer coefficient
In an economizer, ht is typically about 1000Btu/ft2 h °F and h0 is about
15Btu/ft2 h °F.
Let us assume that water temperature tt = 250°F and compute the wall temperature tm for two gas temperatures, 350°F and 750°F.
Tm1 = 350 — (350 — 250)1000 = 252°F m1 1015
Tm2 = 750 — (750 — 250) = 258°F
Hence for a variation of 400°F in gas temperature, the tube wall temperature changes by only 6°F because the gas film heat transfer coefficient is so low compared to the water-side coefficient. Even with finned tubes the difference would be marginal.
We see that if we specify a higher stack gas temperature when selecting or designing an economizer we cannot avoid corrosion concerns if the water temperature is low or close to the acid dew point. A better way is to increase the water temperature entering the economizer by raising the deaerator pressure or by using a heat exchanger to preheat the water.
Using the correlation given below, evaluate the sulfuric acid dew point.
Tdp = 20325 + 276 log PH2O — 1083 log PSO3 — 106 (log PSO3 — 8)
(18b)
The partial pressures are in atmospheres and dew point is in degrees Celsius.
Using the data from Q6.25b [14],
PSO = 0.0031 mmHg = 4.1 x 10-6atm logPSOj = —5.3872 PHO = 93.44 mmHg = 0.1229atm logPHjO = -0.9104 Tdp = 203.25 — 27.6 x 0.9104 — 10.83 x 5.3872 + 1.06 x (2.6128)219 = 128.4°C, or 263°F
How do you convert pollutants such as NOx and CO from gas turbine exhaust gases from mass units such as lb/h to ppm?
With strict emission regulations, plant engineers and consultants often find it necessary to relate mass and volumetric units of pollutants such as NOx and CO. In gas turbine cogeneration and combined cycle plants, in addition to the pollutants from the gas turbine itself, one has to consider the contributions from duct burners or auxiliary burners that are added to increase the steam generation from the HRSGs (heat recovery steam generators).
One can easily obtain the total lb/h of NOx or CO in the exhaust gas. However, regulations refer to NOx and CO in ppmvd (parts per million volume dry) referred to 15% oxygen in the gas. The conversion can be done as follows.
If w lb/h is the flow rate of NOx (usually reported as NO2) in a turbine exhaust flow of W lb/h, the following expression gives NOx in volumetric units on dry basis [9].
V = 100 x(^%MW) (>9)
Where
%H2O = volume of water vapor MW = molecular weight of the exhaust gases
The value of V obtained with Eq. (19) must be converted to 15% oxygen on dry basis to give ppmvd of NOx:
V=________ V x (21 — 15) x 106___________ = V x F (20)
N 21 — 100 x %O2/(100 — %H2O) V 7
Where %O2 is the oxygen present in the wet exhaust gases and factor F converts
V to 15% oxygen basis, which is the usual basis of reporting emissions. Similarly, CO emission in ppmvd can be obtained as
Vc = 1.642 x Vn (for the same w lb/h rate) because the ratio of the molecular weights of NO2 and CO is 1.642.
Determine the NOx and CO concentrations in ppmvd, 15% oxygen dry basis if
CO2 = 3.5, H2O = 10, N2 = 75, O2 = 11.5
Solution. First,
MW = (3.5 x 44 — 10 x 18 — 75 x 28 — 11.5 x 32)/100 = 28 Let us compute NOx on dry basis in the exhaust.
V = 100 x(25/46) = 0.00003074
(550,000/28)/(100 — 10)
F =_______ 106 x (21 — 15__________ = 0.73 x 106
21 -[100/(100 — 10)] x 11.5
Hence
Vn = 0.00003074 x 0.73 x 106 = 22.4 ppmvd Similarly, Vc = (15/25) x 1.642 x 22.4 = 22.0ppmvd.
How can the emissions due to NOx and CO in fired boilers be converted from ppm to lb/MM Btu or vice versa [10]?
Packaged steam generators firing gas or oil must limit emissions of pollutants in order to meet state and federal regulations. Criteria on emissions of common
Pollutants such as carbon monoxide (CO) and oxides of nitrogen (NOx) are often specified in parts per million volume dry (ppmvd) at 3% oxygen. On the other hand, burner and boiler suppliers often cite or guarantee values in pounds per million Btu fired.
Table 6.10 demonstrates a simple method for calculating the conversion. It should be noted that excess air has little effect on the conversion factor.
Table 6.10 shows the results of combustion calculations for natural gas and No. 2 oil at various excess air levels. The table shows the flue gas analysis, molecular weight, and amount of flue gas produced per million Btu fired on higher heating value (HHV) basis. Using these, we will arrive at the relationship between ppmvd values of NOx or CO and the corresponding values in lb/MM Btu fired.
From simple mass-to-mole conversions we have N MW 21 — 3
V-=106 x Y x«x wmx IT—otxt (21)
Where
MW = molecular weight of wet flue gases N = pounds of NOx per million Btu fired
O2 = vol% oxygen in wet flue gases
V n = parts per million volume dry NOx Wgm = flue gas produced per MM Btu fired, lb
Y = 100/(100 — %H2O), where H2O is the volume of water vapor in wet flue gases
|
Table 6.10 Results of Combustion Calculations (Analysis in vol%) Percent excess air
ANatural gas analysis assumed: C = 97, C2 = 2, C3 = 1 vol%. (HHV and LLV = 23,759 and 21,462 Btu/lb, respectively.) BNo. 2 oil analysis assumed: C = 87.5%, H2 = 12.5%; °API = 32. (HHV and LLV = 19,727 and 18,512 Btu/lb, respectively.) |
Wgm = (106/23,789) x 18.3 = 769
Y = 100/(100 — 19.91) = 1.248 MW = 27.53, O2 = 0
Substituting these into Eq. (21) we have
Vn = 106 x 1.248 x N x 27.52 x————————————— — = 832 N
N 46 x 769 x 21
Similarly, to obtain ppmvd CO (parts per million volume dry CO), one would use
28 instead of 46 in the denominator. Thus the molecular weight of NOx would be 46 and the calculated molecular weight of CO would be 28.
Ve = 1367 CO
Where CO is the pounds of CO per MM Btu fired on higher heating value (HHV) basis.
Now repeat the calculations for 30% excess air:
100
TOC o "1-5" h z W = 986 6 Y=———— =1189
Wgm 986 . 6; i 100 — 15 . 96 1189
MW 27 77, O2 4 43
‘2
Vn = 106 x 1.189 x N x 2777 n 46 986.6
18
= 832N
21 -(4.43 x 1.189)
Thus, independent of excess air, we obtain 832 as the conversion factor for NOx and 1367 for CO.
Similarly, for No. 2 oil and using values from Table 6.10,
Vn = 783N and Vc = 1286 CO
If a natural gas burner generates 0.1 lb of NOx per MM Btu fired, then the equivalent would equal 832 x 0.1 = 83 ppmvd.
How can the emissions of unburned hydrocarbons (UHCs) be converted from lb/MM Btu to ppmv basis?
Refer to Table 6.10, which shows the results of combustion calculations for oil and gaseous fuels at various excess air levels. We can obtain UHC emissions on ppmv basis if lb/MM Btu values are known.
Let us assume that U is the emission of UHC (treated as methane) in lb/MM Btu in flue gases of natural gas at 20% excess air. Using Eq. (21) for converting from mass to volume units,
106 x Y x MW x (21 — 3) u = 16 x Wgm x (21 — O2 x Y)
|
|
|
2394 U ppmvd |
27.68 x 18
X 16 x 914 x (21 — 3 .18 x 100/82.92)
For excess air at 10% excess air, MW = 27.62 for flue gases, water vapor = 18.38 vol%, oxygen wet = 1.72 vol% Wgm = 841.
|
|
27.62 x 18
82. 62 x 16 x 841 x (21 — 1.72 x 100/82.62)
= 2365 U ppmvd
Hence, if the UHC value is 0.1 lb/MM Btu for natural gas, it is equivalent to about 237 ppmv.
For No. 2 oil at 20% excess air, Wgm = 938, oxygen = 3.24, MW flue gases = 28.84, water vapor = 11.07 vol%.
R/ „ 1ft6_________________________________ 100________ 28 .84 x 18
V — u x 106 x______ x_____________________________
U 88 . 93 16 x 938 x (21 — 3.24 x 100/88 .93)
= 2240 U ppmvd
Convert SOx values from lb/MM Btu to ppmvd.
Each pound of sulfur in fuel converts to 2 lb of SO2. Using natural gas at 20% excess air, S lb/MM Btu of SO2 is equivalent to
Vs = S x 106 x x 2768 x 18
82.92 64 x 914 x (21 — 3.18 x 100/82.92)
= 598S ppmvd
0.1 lb/MM Btu of SOx is equivalent to 60ppmv. [We are simply using Eq. (21) and substituting for MW and Y.]
Similarly, for No. 2 oil at 20% excess air;
Vs = S x 106 x J™. x , 2884 x 18___________ — = 534S ppmvd
S 88.93 64 x (21 — 3.24 x 100/82.92) pp
A gas turbine HRSG has the following data:
Exhaust gas flow = 500,000 lb/h at 900°F
Gas analysis vol%; CO2 = 3, H2O = 7, N2 = 75, O2 = 15. The exhaust gas has 9lb/h of NOx and CO. The HRSG is fired to 1500°F using natural gas consisting of vol% methane = 97, ethane = 2, propane = 1. Fuel input = 90 MM LHV. HHV of fuel = 23,790 Btu/lb, and LHV = 21,439 Btu/lb. The burner contributes 0.05 lb/MM Btu of NOx and CO. Also see what happens when the burner contributes 0.1 lb/MM Btu of these pollutants. Flue gas analysis after combustion vol% CO2 = 4.42, H2O = 9.78, N2 = 73.91, O2 = 11.86, and flue gas flow = 504,198 lb/h. Compute the NOx and CO levels in ppmvd corrected to 15% oxygen before and after the burner.
We have to convert the mass flow of NOx and CO to volumetric units and correct for 15% oxygen dry basis.
At the burner inlet, using Eqs. (19) and (20),
9 100 28.38 6 21 — 15
Ppmvd NOx = 46 X -9- x 550,000 x 10 x 21 — 15 x 100/93 = 14 7
In this example, the molecular weights of NOx = 46, flue gas = 28.38. The mass of CO remains the same, so ppmvd CO = (46/28) x 14.7 = 24.2.
At the burner exit; the mass of NOx in the exhaust gases after combustion is
23,790
9 + 90 x ——— x 0.05 = 14 lb/h
21,439
Because the burner heat input is on LHV basis and emissions are on HHV basis, we correct the values using the above expression.
|
Ppmvd |
|
— -/V/T, 21 — 15 |
|
X 106 |
|
= 14.4 |
X 21 — 11.86 x 100/90.22 ppmvd CO = (46/28) x 14 = 23.7
With 0.1 lb/MM Btu emissions from the burner, NOx ppmvd = 19.5 and CO ppmvd = 32.1 Thus both the burner contribution and the initial pollutant levels in the turbine exhaust gases affect the ppmv values after combustion. ppmvd values after the burner can be lower or higher than the inlet ppmvd values, though in terms of mass flow they will always be higher.
Steam generator emissions are usually referred to 3% oxygen dry basis, and gas turbine or HRSG emissions are referred to 15% oxygen dry basis. However, in operation, different excess air rates are used that generate flue gases with different oxygen levels. What is the procedure for converting from actual to 3% oxygen basis?
21 — 3
Ppm (@ 3% dry) = ppm (actual) x
21 — O2 (actual)
If dry oxygen in flue gases is 1.7% and 12 ppm of a pollutant is measured, then at 3% oxygen,
|
|
6.27a
In gas turbine cogeneration and combined cycle projects, the heat recovery steam generator may be fired with auxiliary fuel in order to generate additional steam. One of the frequently asked questions concerns the consumption of oxygen in the exhaust gas versus fuel quantity fired. Would there be sufficient oxygen in the exhaust to raise the exhaust gas to the desired temperature?
Gas turbine exhaust gases typically contain 14-16% oxygen by volume compared to 21% in air. Hence generally there is no need for additional oxygen to fire auxiliary fuel such as gas or oil or even coal while raising its temperature. (If the gas turbine is injected with large amounts of steam, the oxygen content will be lower, and we should refer the analysis to a burner supplier.) Also, if the amount of fuel fired is very large, then we can run out of oxygen in the gas stream. Supplementary firing or auxiliary firing can double or even quadruple the steam generation in the boiler compared to its unfired mode of operation [1]. The energy Q in Btu/h required to raise Wg lb/h of exhaust gases from a temperature of t1 to t2 is given by
Q = Wg x (h2 — hx)
Where
Hj, h2 = enthalpy of the gas at tj and t2, respectively
The fuel quantity in lb/h is Wf in Q/LHV, where LHV is the lower heating value of the fuel in Btu/lb.
If 0% volume of oxygen is available in the exhaust gases, the equivalent amount of air Wa in the exhaust is [9]
100 x Wg x O x 32
|
A |
G
23 x 100 x 29. 5
In this equation we are merely converting the moles of oxygen from volume to weight basis. A molecular weight of 29.5 is used for the exhaust gases, and 32 for oxygen. The factor 100/23 converts the oxygen to air.
Wa = 0.0471 x Wg x O (22)
Now let us relate the air required for combustion with fuel fired. From Q5.03- Q.5.05 we know that each MM Btu of fuel fired on HHV basis requires a constant amount A of air. A is 745 for oil and 730 for natural gas; thus, 106/HHV lb of fuel requires A lb of air. Hence Q/LHV lb of fuel requires
Q a hhv.
X A x—— — lb air
TOC o "1-5" h z LHV 106
And this equals Wa from (22).
Q HHV
Q x A x —— = Wa = 0.0471 Wg x O (23)
|
Or |
LHV 106
LHV
Q = 0.0471 x Wg x O x 106 x—————— (24)
^ g Ax HHV
Now for natural gas and fuel oils, it can be shown that LHV/(A x HHV) = 0.00124. Substituting into Eq. (24), we get
Q = 58.4 x Wg x O (25)
This is a very important equation, because it relates the energy input by the fuel (on LHV basis) with oxygen consumed.
It is desired to raise the temperature of 150,000 lb/h of turbine exhaust gases from 950°F to 1575°F in order to double the output of the waste heat boiler. If the exhaust gases contain 15 vol% of oxygen, and the fuel input is 29MM Btu/h (LHV basis), determine the oxygen consumed.
Solution. From Eq. (24),
O =———————- = 3.32%
150,0 x 58.4
Hence if the incoming gases had 15 vol% of oxygen, even after the firing of 29MM Btu/h we would have 15 — 3.32 = 11.68% oxygen in the exhaust gases.
A more accurate method would be to use a computer program [9], but the above equation clearly tells us if there is likely to be a shortage of oxygen.
150,0 lb/h of turbine exhaust gases at 900°F having a gas analysis (vol%) of CO2 = 3, H2O = 7, N2 = 75 and O2 = 15 enters a duct burner, and 35 MM Btu/h (LHV) of natural gas is fired. Determine the exhaust gas analysis after the burner. Use 100% methane as fuel gas analysis for illustrative purposes.
From Table 6.3, the LHV = 21,520 Btu/lb. Hence fuel fired = 35 x 106/ 21,520 = 1626 lb/h.
From combustion basics,
CH4 + 2O2 ! CO2 + 2H2O
So 16 lb of methane requires 64 lb of oxygen and yields 44 lb of CO2 and 36 lb of water vapor, using molecular weights of 16 for methane, 32 for oxygen, 44 for carbon dioxide, and 18 for water vapor. Hence 1626 lb/h of methane will consume
1626 x (64/16) = 6504 lb/h of oxygen
Also, it will increase CO2 by
1626 x (44/16) = 4471 lb/h H2O will increase by
1626 x (36/16) = 3659 lb/h
Convert the volume percent in incoming exhaust gases to weight percent
Basis as follows. The molecular weight of incoming gases is 0.03 x 44 +
0.07 x 18 + 0. 75 x 28 + 0.15 x 32 = 28. 38
Fraction by weight of CO2 = 0.03 x 44/28 . 38 = 0.0465 H2O = 0.07 x 18/28 . 38 = 0.0444 N2 = 75 x 28/28 . 38 = 0 . 74 O2 = 0 .15 x 32/28 . 38 = 0 .1691
The amounts of these gases in incoming exhaust gas in lb/h:
CO2 = 150,000 x 0.0465 = 6975 lb/h H2O = 150,000 x 0.0444 = 6660 lb/h N2 = 150,000 x 0.74 = 111,000 lb/h O2 = 150,000 x 0.1691 = 25,365 lb/h
The final products of combustion will have CO2 = 6975 + 4471 = 11,446 lb/h H2O = 6660 + 3659 = 10,319 lb/h N2 = 111,000
O2 = 25,365 — 6504 = 18,861 lb/h
Total exhaust gas flow = 11,446 + 10,319 + 111,000 + 18,861 = 151,626 lb/h
Which matches the sum of exhaust gas flow and the fuel gas fired.
To convert the final exhaust gas to vol% analysis, we have to obtain the number of moles of each constituent.
Moles of CO2 = 11,446/44 = 260.1 H2O = 10,319/18 = 573. 2 N2 = 111,000/28 = 3964. 3 O2 = 18,861/32 = 589 . 4
Total moles 5387
Hence
CO2 = 260.1/5387 = 0.0483, or 4.83% by volume Similarly,
H2O = 573.2/5387 = 0.1064, or 10.64 vol%
N2 = 3964.2/5387 = 0.7359, or 73.59 vol%
O2 = 589.4/5387 = 0.1094, or 10.94 vol%
Using Eq. (25), we see that nearly 4% oxygen has been consumed [(35 x 106)(58.4/150,000) = 4%] or final oxygen = 15 — 4 = 11%, which agrees with the detailed calculations.
When possible, detailed combustion calculations should be done because they also reveal the volume percent of water vapor, which has increased from 7% to 10.64%. This would naturally increase the gas specific heat or its enthalpy and affect the heat transfer calculations.
Table 6.11 shows the exhaust gas analysis at various firing temperatures.
6.27c
Q:
Determine the final exhaust gas temperature after combustion in the example in Q6.27b.
A:
To arrive at the final gas temperature, the enthalpy of the exhaust gases must be obtained. A simplistic specific heat assumption can also give an idea of the temperature but will not be accurate.
Table 6.11 Effect of Firing Temperature on Exhaust Gas Analysis
|
Firing temperature,°F |
||
|
1400 |
1800 2200 2600 |
3000 |
|
Burner duty, MM Btu/h |
22.5 |
41.83 |
62.98 |
86.54 |
111.1 |
|
Total gas flow, lb/h |
151,037 |
151,947 |
152,935 |
154,035 |
155,174 |
|
H2O, vol% |
9.33 |
11.29 |
13.39 |
15.67 |
18.00 |
|
CO2, vol% |
4.19 |
5.18 |
6.26 |
7.42 |
8.6 |
|
O2, vol% |
12.38 |
10.18 |
7.83 |
5.27 |
2.67 |
150,000lb/h of exhaust gases at 900°F. Exhaust gas analysis (vol%): CO2 = 3, H2O = 7, N2 = 75, O2 = 15. Natural gas: C1 = 97 vol%, C2 = 3 vol%.
Using, say, 0.3 Btu/lb °F for the average gas specific heat for the temperature range in consideration, the increase in gas temperature is
35 x 106/(150,000 x 0.3) = 777°F
Or
Final gas temperature = 900 + 777 = 1677°F
However, let us use gas enthalpy calculations, which are more accurate. Figure
6.3 shows the gas enthalpy for the turbine exhaust gas at various temperatures. (A program was used to compute these values based on the enthalpy of individual constituents.) Enthalpy of exhaust gas at 900°F = 220 Btu/lb.
From an energy balance across the burner;
150,0 x 220 + 35 x 106 = 151,626 x hg
Where hg = enthalpy of final products of combustion. hg = 448.5 Btu/lb. From the chart, the gas temperature = 1660°F.
A computer program probably gives more accurate results, because it can compute the gas temperature and enthalpy for any gas analysis and iterate for the actual enthalpy, whereas a chart can be developed only for a given exhaust gas analysis and a maximum firing temperature.
|
600 — |
|
|
500 — |
|
|
A E; |
|
|
3 |
400 ‘ |
|
G |
|
|
30D — |
|
|
I Rtп |
|
|
200 — |
|
|
100 — |
0 H———— 1———— 1———- 1———- 1———— 1———- 1———- 1———— 1———- 1
300 500 700 900 1100 1300 1500 1700 1900
Gastemperature, T
FIGURE 6.3 Enthalpy of turbine exhaust gas as a function of temperature.
How can the fuel consumption for power plant equipment such as gas turbines and diesel engines be determined if the heat rates are known?
The heat rate (HR) of gas turbines or engines in Btu/kWh refers indirectly to the efficiency.
3413
Efficiency =
HR
Where 3413 is the conversion factor from Btu/h to kW. One has to be careful about the basis for the heat rate, whether it is on HHV or LHV basis. The efficiency will be on the same basis.
If the heat rate for a gas turbine is 9000 Btu/kWh on LHV basis and the higher and lower heating values of the fuel are 20,000 and 22,000 Btu/lb, respectively, then
3413
Efficiency on LHV basis = 9— = 0.379, or 37.9%
To convert this efficiency to HHV basis, simply multiply it by the ratio of the heating values:
Efficiency on HHV basis = 37.9 x 20,000 = 34.45%
22,000
|
A |
Theoretical amount of air for combustion per MM Btu fired, lb |
|
C, CO, CO2 |
Carbon, carbon monoxide, and carbon dioxide |
|
Ca |
Ash concentration in flue gas, grains/cu ft |
|
CP |
Specific heat, Btu/lb °F |
|
E |
Emission rate of sulfur dioxide, lb/MM Btu |
|
E |
Excess air, % |
|
EA |
Excess air factor |
|
HHV |
Higher heating value, Btu/lb or Btu/scf |
|
HR |
Heat rate, Btu/kWh |
|
Hi; ho |
Inside and outside heat transfer coefficients, Btu/ft2 h °F |
|
K |
Constant used in Eq. (7) |
|
K1, K2 |
Constants used in Eq. (10a) and (10c) |
|
L1-L5 |
Losses in steam generator, % |
|
LHV |
Lower heating value, Btu/lb or Btu/scf |
|
MW |
Molecular weight |
|
Pc ; Pw, PH2O |
Partial pressures of carbon dioxide and water vapor, atm |
|
PSO3 |
Partial pressure of sulfur trioxide, atm |
|
Pa; Ps |
Actual and standard pressures, psia |
|
DP |
Differential pressure, psi |
|
Q |
Heat loss, Btu/ft2 h |
|
Q |
Energy, Btu/h or kW |
|
S |
Specific gravity |
|
S |
Sulfur in fuel |
|
Ta; tg |
Temperatures of air and gas, °F |
|
Tm |
Melting point of ash, °C; tube wall temperature, °C |
|
Tdp |
Acid dew point temperature, K |
|
T T Sa |
Standard and actual temperatures, °R |
|
V V Sa |
Standard and actual volumes, cu ft |
|
V V R c r n |
CO and NOx ppmvd |
|
W |
Weight of air, lb/lb fuel; subscript da stands for dry air; wa, wet air; wg, wet gas; dg, dry gas |
|
W |
Moisture, lb/h |
|
Wa; Wg; Wf |
Flow rates of air, gas, and fuel, lb/h |
|
Z |
Efficiency; subscripts HHV and LHV denote the basis |
|
P |
Density, lb/cu ft; subscript g stands for gas, f for fuel |
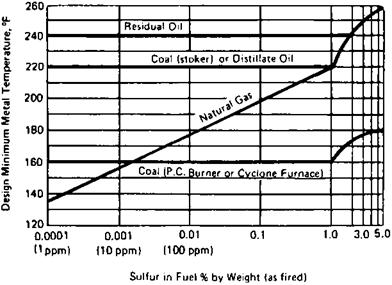
Опубликовано в рубрике 
