Ясно, что расчеты, проведенные по теории Шмидта, приближенные и имеют ограниченное значение, поскольку реальные параметры составляют 0,3—0,4 расчетных. Вследствие этого были предприняты попытки разработать более совершенный метод. Подробное рассмотрение этого вопроса выходит за рамки данной книги, но все же его краткое изложение, отвечающее пожеланиям специалистов, работающих в этой области, будет сделано.
О теоретических разработках и исследованиях фирмы «Филипс» известно очень мало. При описании двигателя и криогенной газовой машины Мейер в 1969 г., Келлер (КбЫег) в 1955 г. пользовались методом, основанным или близким к теории Шмидта. Шелк — вийк (Schalkwijk, 1959 г.) и Кёллер (1965 г.) опубликовали материал, относящийся к работе регенеративных теплообменников применительно к машинам с циклом Стирлинга. Мейер ссылается на успешные теоретические разработки и моделирование двигателей на ЭВМ при. оптимизации конструкции, однако подробностей в открытой литературе нет и маловероятно, что они будут опубликованы в ближайшем будущем. Умение осуществить точное моделирование реального двигателя, возможно, является одной из главных притягательных сторон потенциальных лицензий фирмы «Филипс», и, вполне вероятно, эта методика останется засекреченной, что связано с сохранением коммерческой тайны.
Из числа открыто опубликованных работ по дальнейшему совершенствованию теоретического анализа, несомненно, наиболее важный вклад за последние 20 лет был сделан Финкельштейном; перечень его работ приводится в списке литературы. Основываясь на теории Шмидта, Финкельштейн впервые дал обобщенный анализ, учитывающий неизотермичность процессов сжатия и расширения. Эта теория была исследована Уокером и Ханом (Khan) в 1965 г., где, в частности, особое внимание было уделено предельному случаю адиабатного сжатия и расширения. Так, например, выяснилось, что в двигателе с изотермическими процессами сжатия и расширения термический к. п. д. для циклов Шмидта и Карно равнялся 50%, а при соответствующих адиабатных процессах этот к. п. д. был равен 34,3%. Аналогичным образом холодильный коэффициент криогенной газовой машины уменьшается от 1 при изотермических процессах до 0,543 при адиабатных процессах. Кроме того, как термический к. п. д., так и холодильный коэффициент становятся функциями всех конструктивных параметров, включая a k и К, хотя по теории Шмидта они были лишь функциями т. Потенциальные возможности этой простой теории никогда не были полностью использованы, и, вероятно, при дальнейшем развитии в нее может быть внесено много дополнений.
Последующее развитие теоретического анализа связано с публикацией в 1964 г. Финкельштейном ряда работ, в которых указывается метод подробного математического описания тепловой регенеративной машины с помощью 39 параметров и 4 функций; решение по этому методу получено в виде функциональных зависимостей 28 зависимых переменных. Эта теория, как известно, до сих пор не используется систематически.
|
Рис. 4-1. Отдельные части микроохладителя, работающего по циклу Стирлинга. / — регенератор; 2 — полость сжатия; 3 — рабочий поршень; 4 — полость расширения; 5 — холодильник; 6 — шток вытеснителя. |
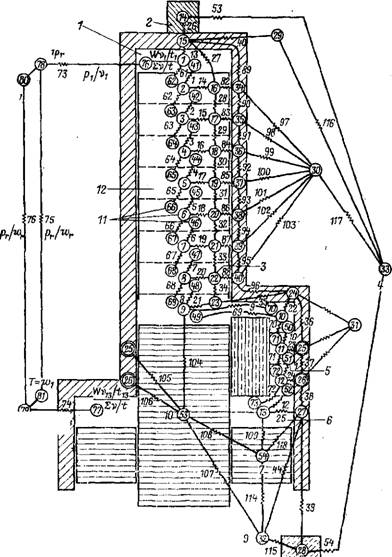
Впоследствии Финкельштейн занимался вопросами моделирования на аналоговой ЭВМ, а много позже усовершенствованием хо-. рошо известной программы теплового анализа ТАР (Thermal Analysis Program) и применением ее к машинам с циклом Стирлинга. Финкельштейн усовершенствовал программу моделирования до рабочего состояния; эта программа была использована автором для оптимизации микроохладителей. Подробное ее описание приведено в работах Финкельштейна, Уокера и Йоши (Joshi) в 1970 г. Программа требует детальной конструктивной проработки машины. Далее согласно программе машина для возможно более точного описания изменения температуры и давления разбивается на ряд узловых, достаточно малых контрольных объемов; при этом они не должны быть слишком большими, так как в противном случае из-за замены непрерывных функций дискретными точками появляются значительные ошибки. Газовые полости машины, ее отдельные части и внешняя окружающая среда рассматриваются как неизменный ряд изотермических зон с расчетной теплоемкостью, между которыми из-за разности температур происходит теплообмен теплопроводностью и конвекцией. В качестве примера на рис. 4-1 показаны общий вид и отдельные части микроохладителя, а на рис. 4-2 — схема контрольных объемов для его моделирования. Программа достаточно хорошо позволяет осуществить и моделирование работы теплового регенеративного двигателя; она может быть применена также к любой схеме машины с открытым и с замкнутым циклами. Для осуществления моделирования по этой программе требуется высокоскоростная цифровая ЭВМ с запоминающим устройством; при работе в университете Калгари на машине IBM 360/50 для каждого цикла требовалось от 6 до 40 мин машинного времени. Основная трудность состоит в том, что большое количество данных по теплопередаче и газовому потоку рабочего тела, вводимых в машину, неизвестны. Таким образом, нет возможности без экспериментальной проверки оценить точность моделирования; когда же имеется экспериментальная установка, большой необходимости в ЭВМ нет. Конечно, об этом можно говорить после, того, когда предсказываемые программой данные будут достаточно хорошо согласовываться с экспериментальными, и лишь тогда она может использоваться для оптимизации при проектировании экспериментальных установок. Это отчасти верно, по степень погрешности увеличивается в зависимости от того, насколько условия, вводимые в программу, отличаются от условий в экспериментальной уста-
|
T^w |
|
Рис. 4-2 Схема узловых точек для моделирования микроохладителя иа цифровой ЭВМ (по Финкельштейну, Уокеру и Йоши, 1970 г.). ‘ — расширения; 2 — детектор; 3 — узловые точки насадки; 4 — атмосфера- (-холодильник; в- полость сжатия; 7 — рабочий поршень; 8 — картер коленч^го вала; 9 — привод; /Й — вытеснитель; 11 _ узловые точки газа; 12 — регенератор |
|
Т=го, С=1/к |
|
Т73=ыЫр; CyS-l/K‘Zpr |
|
Я уЛУ/У/Л |
Новке, так как оценивающие модель «надуманные» факторы не остаются постоянными.
‘ Существенный вклад в развитие теоретического анализа был сделан также Квейлом и Смитом в 1969 г., а также Риосом (Rios) и Смитом в 1969 г., рассматривавшими основной цикл с адиабатными процессами сжатия и расширения. Особое внимание в их работах было уделено вопросам необратимости процессов. Такой подход предусматривает независимое изучение отдельных вопросов теплообмена методом последовательных приближений, который может быть выполнен с требуемой степенью сложности.



 12 ноября, 2012
12 ноября, 2012  admin
admin 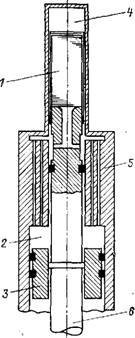
 Опубликовано в рубрике
Опубликовано в рубрике