Процесс самовозгорания принципиально не отличается от процесса самовоспламенения. Оба этих процесса характеризуются одинаковыми закономерностями возникновения и развития.
Разделение этих процессов условно. Оно основано на величине температуры начала их развития. Если процесс возникновения горения в отсутствие внешнего источника начинается при температуре выше 100 °С, его обычно называют самовоспламенением, если при температуре ниже 100 °С — самовозгоранием.
Самовозгораться могут вещества в различном агрегатном состоянии: газы, жидкости и твердые. Самовозгорающиеся при нормальной температуре газы называются пирофорными.
Если температура реагирующей системы меньше температуры окружающей среды, то для развития процесса самовозгорания необходимо наличие прогрева, протекающего в четыре стадии (рис. 3.5):
1. Прогрев системы от внешнего источника тепла в результате теплообмена с окружающей средой. Выделением тепла за счет химической реакции на этой стадии пренебрегается.
2. Прогрев вещества за счет внешнего и внутреннего источника. Внутренним источником является тепло от начавшейся химической реакции.
3. Саморазогрев системы за счет химической реакции с теплопоте-рями в окружающую среду.
4. Адиабатический саморазогрев системы.
59
Корольченко А. Я. Процессы горения и взрыва
Анализ этих стадий наиболее удобно выполнить по схеме, разработанной профессором В. И. Горшковым, введя безразмерные переменные температуры ![]()
|
|
(3.24)
|
|
И времени ![]()
(3.25)
Где Т* — температура в точке касания кривых тепловыделения и теплоот-вода по диаграмме Семенова (рис. 3.1, точка С) ; Т — Текущая температура; Q — Тепловой эффект реакции, Дж/кт*К; р — Плотность материала, кг/м3; К0 — Предэкспоненциальный множитель, 1/с; С — теплоемкость материала, дж/кг К; T — текущее время, с.
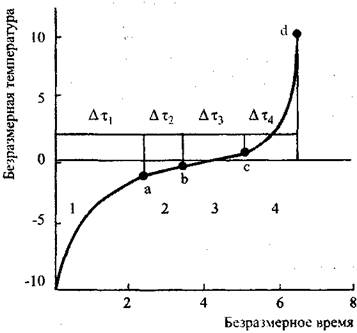
Рис. 5.5. Изменение температуры системы при наличии Стадии прогрева (точками отмечены границы стадий)
60
Глава 3. Возникновение процессов горения
Схема профессора В. И. Горшкова предполагает оценку периода индукции — промежутка времени от начала процесса до самовозгорания. Период индукции представляет собой сумму времен ![]() (рис. 3.5). Общее выражение для периода индукции имеет вид:
(рис. 3.5). Общее выражение для периода индукции имеет вид:
![]() (3.26)
(3.26)
Где ![]() — безразмерная температура окружающей среды
— безразмерная температура окружающей среды
![]()
Для стадии прогрева 1 при отсутствии химической реакции в соответствии с формулой (3.26) можно записать
![]() . , (3.27)
. , (3.27)
Интегрирование которого с учетом начальных условий ![]() И
И ![]() Цает:
Цает:
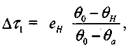 (3.28)
(3.28)
Где ![]() — ч неизвестная пока температура в точке
— ч неизвестная пока температура в точке ![]() На диаграмме —Рис. 3.5.
На диаграмме —Рис. 3.5.
Для расчета времени прогрева системы на стадии 2 экспоненту (уравнение 3.26) нужно разложить в ряд в окрестности точки ![]() И, ог-
И, ог-
Раничившись линейной частью ряда, получить
![]() (3.29)
(3.29)
При подстановке соотношения (3.29) в формулу (3.26) имеем
![]() (3.30)
(3.30)
61
Корольченко А. Я. Процессы горения и взрыва
Для определения неизвестных значений температур на границах стадий учтем, что на границах этих участков равны не только температуры вещества, но и их производные по времени. Поэтому с учетом уравнений (3.27) и (3.30), для точки а справедливо соотношение
![]() (3.31)
(3.31)
Откуда ![]()
Для Ахь Подставив формулу (3.31) в уравнение (3.28), получим:
![]() (3.32)
(3.32)
Путем интегрирования уравнения (3.30) найдем время задержки воспламенения на втором участке:
|
|
(3.33)
Решение уравнения (3.30) с учетом, что ![]() (см. формулу
(см. формулу
3.31), получаем:
![]() (3.34)
(3.34)
Время задержки самовозгорания на участке 3 можно определить методом разложения экспоненты в ряд в окрестности точки ![]()
![]() (3.35)
(3.35)
Уравнение (3.26) может быть представлено в виде:
![]() (3.36)
(3.36)
Поскольку левые части уравнений (3.36) и (3.30). равны, то, приравнивая правые части, определим температуру в точке В:
![]() (3.37)
(3.37)
62
Глава 3. Возникновение процессов горения
. Из формул (3.34) и (3.37) найдем время, затрачиваемое реакцией на преодоление участка 2:
|
|
(3.38)
На участке 4, в условиях адиабатического разогрева вещества, экспоненту разложим в ряд Тейлора в окрестности точки ![]() И ограничимся тремя первыми членами разложения:
И ограничимся тремя первыми членами разложения:
![]() (3.39)
(3.39)
С учетом адиабатичности процесса теплоотдачей в окружающую среду при рассмотрении этого участка можно пренебречь и принять в формуле (3.26) ![]()
Тогда, в соответствии с формулами (3.26) и (3.39) получаем:
|
|
(3.40)
Поскольку в точке ![]() Производные по температуре равны, приравняв уравнения (3.36) и (3.40), имеем:
Производные по температуре равны, приравняв уравнения (3.36) и (3.40), имеем:
![]() (3.41) и, соответственно, время на участке 3 равно:
(3.41) и, соответственно, время на участке 3 равно:
|
|
(3.42)
Поскольку ![]() Определяется соотношением (3.37).
Определяется соотношением (3.37).
Интегрирование уравнения (3.40) позволяет оценить время адиабатического разогрева:
|
|
(3.43);:
На участке 4 происходит неограниченное возрастание скорости реакции. Поэтому в качестве верхнего предела интегрирования можно при-
63
Корольченко А. Я. Процессы горения и взрыва
Нять бесконечность. С учетом этого обстоятельства и приняв во внимание, что на рассматриваемом участке ![]() Получаем:
Получаем:
![]() (3-44) Период индукции теплового самовозгорания получим как сумму
(3-44) Период индукции теплового самовозгорания получим как сумму
![]()
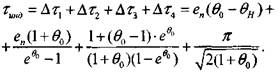 (3.45)
(3.45)
Формула (3.45) применима для условий:
![]()
В качестве причин, приводящих к самовозгоранию, могут быть: внешний нагрев, теплота реакции окисления, тепловой эффект экзотермической реакции, микробиологический процесс. В соответствии с этим различают:
• тепловое самовозгорание,
• химическое самовозгорание,
• микробиологическое самовозгорание.



 5 мая, 2013
5 мая, 2013  admin
admin 
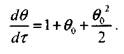
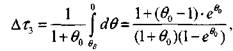
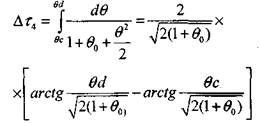
 Опубликовано в рубрике
Опубликовано в рубрике