Рассмотрим развитие процесса самовоспламенения во времени, т. е. нестационарную задачу, имея в виду следующую физическую модель. Реагирование одновременно происходит по всей массе некоторого ограниченного объема газовой горючей смеси определенного начального состава и температуры.
Тепло, выделяющееся при химическом реагировании в смеси, заключенной в некотором сосуде, расходуется на нагрев смеси и частью отводится через стенки сосуда, поэтому уравнение баланса тепла для реагирующей смеси можно записать в следующем виде:
<2р—<3н—<3т = 0. (5-48)
В уравнении (5-48):
(2Р — количество выделяющегося тепла;
<3н—количество тепла, расходуемое на нагрев смеси;
(2т — количество тепла, отводимое через стенки сосуда в окружающую среду.
Рассматривая реакцию между горючим газом и кислородом как реакцию второго порядка и пренебрегая расходом реагентов до наступления самовоспламенения, подставляя в уравнение (5-48) выражения для отдельных составляющих и относя его к единице объема и времени, получаем:
Ке~Е1КТ С"Г00, (-ур)’ С — — Сем — а (Г — Т,) ± = 0, кВт/м*.
Начальное условие: при т=0, Т=Т^
В уравнении (5-49):
Р/П^
&0в —константа скорости реакции;
Е — энергия активации, кДж/моль;
# = 8,321—универсальная газовая постоянная, кДж/(моль-К);
С°г и С0а —концентрация горючего и кислорода, кг/м3, при давлении 0,1013 МПа и температуре 0°С;
Ту — начальное значение температуры смеси и равная ей температура стенок сосуда, К;
Т — текущая температура смеси, К;
(2 — теплота сгорания смеси, кДж/кг;
Сем — теплоемкость смеси, кДж/(м3-К);
Т — время, с;
А — коэффициент теплоотдачи от стенки в окружающую среду, кВт/ (м2-К);
5 и V — поверхность и объем реакционного сосуда, м2 и м3.
Переходя к безразмерным температуре, координате и коэффициенту теплоотдачи, можно уравнение (5-49) представить в следующем безразмерном виде:
Е~!/0—————- й (6 — 61) == 0. (5-50)
Йх
В уравнении (5-50):
6 — Т? Т/Е — безразмерная температура;
ХАоС°гС^0 2732Я<Э
Т =.———- ёалТ Е———— безразмерное время;
А Е Б
□=———————- <27ъ ■; 2—- гг —безразмерный коэффициент теплоотдачи.
КоС°гС ^
Начальное условие: при т=0 0 = 01.
Решение уравнения (5-50) будет иметь вид:
Е = 6й 61) (5-51)
И даст в безразмерных координатах изменение температуры горючей смеси во времени.
Прежде чем сделать выводы, для полноты исследований рассмотрим процесс самовоспламенения при постоянном давлении как химическое реагирование в горючей смеси определенного начального состава и температуры при продувании ее через цилиндрическую камеру. При этом температура стенок камеры поддерживается одинаковой с начальной температурой смеси.
Такой подход имеет интерес и в связи с тем, что в экспериментальных работах обычно применяется метод изучения самовоспламенения в прямоточных камерах.
Резкое повышение температуры при самовоспламенении может тур — булизировать поток и в области больших градиентов температур нарушить одномерный аэродинамический и тепловой характер течения. При искривлении профиля температур в поперечном сечении и турбулиза — Ции потока возникает турбулентный массо — и теплообмен и нарушается дальнейшее развитие процесса самовоспламенения последующих порций горючей смеси. Процесс переходит в стадию воспламенения при наличии фронта пламени.
Для аналитического исследования примем описанную выше модель процесса самовоспламенения в основу математической модели с одномерным течением.
Экспериментальная проверка теории, основанной на одномерной модели, может быть осуществлена проведением опытов в камере не до наступления развитого воспламенения, а до прироста температуры на характерную величину, после которой процесс самовоспламенения наступает. Другим экспериментальным методом может быть периодическое ведение опытов с перерывом их в момент наступления самовоспламенения. Такое ведение опытов будет отвечать самовоспламенению отдельных порций горючей смеси.
Считая, что в период воспламенения расходом горючего газа и кислорода можно пренебречь, уравнение (5-48) для элементарного участка камеры в развернутом виде Д. М. Хзмаляном представлено как
К, е-е"1Тс, тс (-^-)а<г ^-<1х —
— 1Г ~ Ссы «га (Т — Т,)Лх = 0, кВт. (5-52)
В уравнении (5-52):
Й — диаметр камеры, м;
№—скорость потока, м/с;
А—коэффициент теплоотдачи от газов к стенке, кВт/(м2-К).
Относя уравнение (5-52) к единице объема, получим:
К, е~Е1ЯГСС^-Уй-ш, сш~——————- £(7’-7) = 0, (5-53)
Где то — скорость потока, м/с (при давлении 0,1013 МПа и температуре 0°С).
Начальное условие: при л: = 0 Т = Т±.
Переходя к безразмерной температуре, координате и коэффициенту теплоотдачи, получаем:
В“1 /в —^—— О (в — в,) = 0. (5-54)
В уравнении (5-54):
6 = ИТ[Е — безразмерная температура;
ЬпСЪ. Со 97^2 £>зп
И = х——— -————— — — безразмерная координата;
ШоСалЕ*
Й 0 2732(Э — безразмерный коэффициент теплоотдачи.
Начальное условие: при к — 0 0 = 01.
Уравнение (5-54) можно использовать и для исследования самовоспламенения пылевоздушной смеси в одномерном потоке. Примем в качестве топлива пыль АШ и сделаем следующие предположения. Частицы сферической формы; во входном сечении прямоточной камеры концентрация пыли, а также скорость и температура пылевых частиц, которые одинаковы со скоростью и температурой в потоке, распределены равномерно и известны.
Из-за того что в угольной пыли обычной тонкости основную массу представляют мелкие фракции, можно считать, что температура реагирующих пылевых частиц мало отличается от температуры газа, т. е.
77
В ходе реагирования температура газа повышается вместе с температурой частиц, сохраняясь одинаковой с ней; в период, предшествующий воспламенению, выгорание мало и расходом угольной пыли и кислорода на реагирование можно пренебречь. Процесс самовоспламенения развивается в кинетической области. Для учета выхода и выгорания летучих для кинетических констант (Ко и Е) взяты их эффективные значения.
В этом случае согласно [Л. 12, 13] уравнение (5-48) в развернутом виде, отнесенное к единице объема, записывается в виде
(^~у <ГЕ/ет — ю. (с. + №„) ———————— (Г — Г.) = 0, кВт/м».
Начальное условие: при х = 0 Т = Т.
В уравнении (5-55):
(3 —стехиометрический коэффициент, показывающий отношение массы прореагировавшего топлива к массе израсходованного кислорода;
&0е~£/7?г— константа скорости реакции, м/с;
С0 и ро — соответственно концентрации кислорода и угольной пыли, кг/м3;
И фрн — поверхность и теплота сгорания угольной пыли, м2/кг и кДж/кг;
Ш0 — скорость потока при давлении 0,1013 МПа и температуре 0°С, м/с;
Св и сп — соответственно теплоемкость воздуха и пыли, кДж/(м3-К) и кДж/(кг*К).
•В безразмерном виде уравнение (5-55) совпадает с уравнением (5-54), при этом безразмерная координата
|
|
|
![]()
Таким образом, уравнения (5-50) и (5-54) являются универсальными и могут быть использованы для аналитического исследования процесса самовоспламенения как газовых, так и пылевоздушных смесей.
Наиболее благоприятные условия для развития самовоспламенения будут иметь место при отсутствии теплоотвода в стенки камеры. Приняв в (5-54) Й=0, получим уравнение для адиабатического условия в следующем виде:
|
В |
![]() (5-56)
(5-56)
В уравнении (5-56) явно не содержатся константы, отражающие свойства топлива, и параметры, характеризующие режимные условия, они входят в состав безразмерной координаты. Поэтому из его решения в безразмерных координатах
Можно получить решение нестационарной задачи о самовоспламенении любого топлива при любых режимных условиях.
|
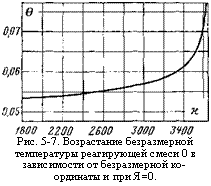
Рис. 5-7. Возрастание безразмерной температуры реагирующей смеси 0 в зависимости от безразмерной координаты и при Я=0. |
 Уравнение (5-56) допускает разделение переменных, но не интегрируется в квадратурах, поэтому было применено численное интегрирование на электронной вычислительной машине [Л. 14].
Уравнение (5-56) допускает разделение переменных, но не интегрируется в квадратурах, поэтому было применено численное интегрирование на электронной вычислительной машине [Л. 14].
|
Рис, 5-8. Универсальная зависимость для температуры самовоспламенения 01 от безразмерной длины участка хСв, предоставляемого для развития процесса воспламенения при 0 = 0. |
|
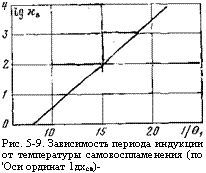
Рис. 5-9. Зависимость периода индукции от температуры самовоспламенения (по ‘Оси ординат 1дхсв)- |
 Из решения уравнения для одного, а именно меньшего, значения начальной безразмерной температуры 01, приведенного графически на рис. 5-7, используя аддитивные свойства интеграла, можно также получить решение для любого большего значения 0ь как соответствующий участок основной кривой 0 = 0 (х, 0!). Кривая 0=10 (х, 01) плавно и со все возрастающим темпом поднимается вверх. Резкий подъем температурной кривой означает наступление самовоспламенения. Значения величины координаты х, при которой наступает самовоспламенение, т. е. длина участка самовоспламенения хсв и, следовательно, соответствующий период индукции, уменьшаются с повышением температуры 0ь Поэтому при определении длины участка самовоспламенения необходимо указывать температуру, которой она соответствует. Например, длину участка самовоспламенения при начальной температуре смеси 01 будем обозначатьх®1.
Из решения уравнения для одного, а именно меньшего, значения начальной безразмерной температуры 01, приведенного графически на рис. 5-7, используя аддитивные свойства интеграла, можно также получить решение для любого большего значения 0ь как соответствующий участок основной кривой 0 = 0 (х, 0!). Кривая 0=10 (х, 01) плавно и со все возрастающим темпом поднимается вверх. Резкий подъем температурной кривой означает наступление самовоспламенения. Значения величины координаты х, при которой наступает самовоспламенение, т. е. длина участка самовоспламенения хсв и, следовательно, соответствующий период индукции, уменьшаются с повышением температуры 0ь Поэтому при определении длины участка самовоспламенения необходимо указывать температуру, которой она соответствует. Например, длину участка самовоспламенения при начальной температуре смеси 01 будем обозначатьх®1.
На рис. 5-8 показана зависимость начальной температуры, при которой происходит самовоспламенение, от длины участка хсв (периода индукции). Этот график является универсальным для различных топлив и режимные параметров.
Перестроив кривую 01 = /(хсв) в координатной системе 1§Исв = /(01) {рис. 5-9), получим зависимость для определения периода индукции, необходимого для обеспечения воспламенения при начальной температуре 01:
1г ХСВ = — 2,36 + 0,292 -1-. (5-58)
Отсюда температура самовоспламенения при заданном периоде индукции может быть определена как
0,292 (5-59)
Для исследования процесса самовоспламенения в камере при наличии теплоотвода в стенки и влияния аппаратурных условий было численно проинтегрировано на ЭВМ также и уравнение (5-54) [Л. 13, 14]. Пределы изменения значения безразмерного коэффициента теплоотвода, представляющие практический интерес, составляют 0 = 0—270[2] 10~4, а начальной безразмерной температуры 01=0,052; 0,058; 0,0642; 0,070; 0,076.
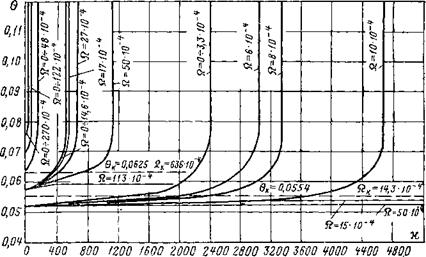
Результаты численного интегрирования уравнения (5-54) приведены в виде графиков на рис. 5-10. Как видно, кривые возрастания тем-
|
Рис. 5-10. Возрастание безразмерной температуры реагирующей смеси по безразмерной длине камеры. |
Пературы по длине камеры подразделяются на два типа. При высокой интенсивности теплоотвода после некоторого повышения температура стабилизируется, т. е. самовоспламенения не происходит. При меньших значениях интенсивности теплоотвода й, после медленного нарастания температуры на некотором участке температурная кривая плавно и со все возрастающим темпом поднимается вверх, что означает наступление самовоспламенения. При этом, чем меньше £1, тем меньше период индукции. Наибольшее значение йк, при котором еще возможно самовоспламенение при данном значении 01, является критическим и разграничивает режимы на две области: при й>йк самовоспламенение не может совершиться, процесс характеризуется достижением стационарной температуры смеси 0К, несколько превышающей температуру 81, а при &<йк самовоспламенение может наступить.
Интенсивность теплоотвода характеризуется долей тепла, передаваемой в окружающую среду, от общего тепловыделения
Аппаратурные условия могут быть охарактеризованы долей тепла реакции, идущего на нагрев смеси (рис. 5-11):
|
В уравнении (5-61): (Зн — количество тепла, идущего на нагрев смеси за единицу вре- (2Р — тепловыделение; Q = tgф — интенсивность теплоотвода при данных аппаратурных: £2к==^фк — критическая интенсивность теплоотвода. При адиабатических условиях £2 = 0, <7н=1, т. е. все тепло, выделяю- Мальным. В стационарном состоянии в кри Нения, интенсивность теплоотвода рав- Выражено тепловыделение, а пря — О Начальной температуры смеси 01 и ЙС}р/йТ равняется интенсивности теплоотвода й(2т/(1Т, выражаемой угло- С повышением начальной температуры при той же интенсивности Проведя из точки 0“ касательную к кривой (2Р и опустив из точки <Зн |
|
50 |
|
40 |
|
О |
|
0,с |
|
% |
|
(5-62) |
|
Ян |
|
|||
|
|
||
|
|||
 |
Пламенения, свободных от влияния аппаратурные условий и отражающих реакционные свойства топлив и влияние физических параметров, опыты следует проводить в камере с d>dK.
Следовательно, начальная температура смеси, при которой самовоспламенение возможно зависит от. свойств топлива, физических условий, периода индукции и аппаратурных условий, т. е.
Be*=f(K.,E; С0; ,*0;/; *; q*). (5-63)
Для однозначного определения температуры самовоспламенения необходимо оговорить период индукции, задав его значение ограниченной, практически приемлемой величиной, а также оговорить аппаратурные условия величиной <7н —0,9-М.
Начальная температура Т, при которой в процессе реагирования в условиях, близких к адиабатическим, самопроизвольный разогрев может быть достигнут в течение определенного периода индукции своей
RT2
Критической величины Д7’к=-^2, называется температурой на пределе
Воспламенения, а температура ТК=Т +АГК, после которой скорость реакции резко увеличивается, называется температурой самовоспламенения.
Значения температур самовоспламенения, удовлетворяющие данному ее определению, зависят от свойств топлива и режимных параметров и поэтому могут быть признаны физико-химическими константами. Температуру самовоспламенения различных топлив можно определить по универсальному графику, приведенному на рис. 5-9, описываемому формулой (5-59).
Предельное повышение температуры при режиме с отсутствием самовоспламенения можно определить решением стационарной задачи для данных условий. В уравнении (5-54), опуская второй, нестационарный член, находят параметры стационарного состояния на пределе воспламенения из условия равенства тепловыделения теплоотводу и равенства их первых производных по температуре, т. е.
<Г V=(0„ — 6«,) (5-64)
И
В уравнениях (5-64) и (5-65):
0Ki — критическое значение начальной безразмерной температуры;
0К — температура смеси на пределе воспламенения;
QK — критическая безразмерная интенсивность теплоотвода.
Совместное решение уравнений (5-64) и (5-65) дает величину са — моразогрева на пределе воспламенения:
Переходя в уравнении к размерным величинам и пренебрегая малой величиной RTfE по сравнению с единицей, получаем величину са — моразогрева, равную
АТк = -?р. (5-67)
Соотношение (5-67) следует понимать так, что если самопроизвольный разогрев реагирующей смеси достигнет АТк, то самовоспламенение
Станет возможным. В противном случае самовоспламенение не наступит.
Заметим, что в выражение критического саморазогрева (5-67) не входят аппаратурные и режимные параметры и период индукции. Величина критического разогрева зависит лишь от реакционных свойств топлива. Это означает, что в любых аппаратурных и режимных условиях самовоспламенение может совершиться после достижения критической величины самопроизвольного разогрева АТк.
Период индукции, необходимый при данной величине начальной температуры для достижения саморазогрева АТк, после которого процесс переходит в стадию воспламенения, зависит от аппаратурных и. режимных условий и рода топлива.



 8 апреля, 2013
8 апреля, 2013  doctype
doctype 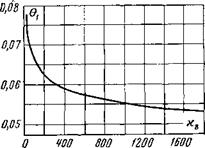
 Опубликовано в рубрике
Опубликовано в рубрике