Система уравнений (3.4) может быть упрощена путем исключения одной из переменных прп помощи конечного соотношения, приведенного в последней строке. Выразив 6q из четвертого уравнеиия и подставив его во второе, получим равенство

" лГ 0 Эх ) Ср ^ <?г faj 1 Аг

Второе слагаемое в левой части которото равно нулю в силу третьего уравнения системы (3.4). Множитель

Си Qo 1

При первом слагаемом равеп — —=-у, где я —скорость

Ср рч а

Звука в не возмущенном течении. Это следует пз извест­ных термодинамических соотношений:

(4.1) (4-2)

(4-3)

(газовая постоянная R здесь отнесена к единице массы, а не веса).

Таким образом, после исключения $е системе (3.4) можпо придать следующий впд:

Dbv. dbv. і дЬй А ї dtp .Oft p. о dbv n

F? Ss, dbs Л dt 1 0 dx

(4.4)

Особенностью полученной системы являстся то, что вследствие выбора в качестве зависимых переменных нелпчтш fiL>, bp и 6s первые два уравпешш могут быть проинтегрированы отдельпо от третьего. Это обстоятель­ство заметно упрощает вычисления. Физический смысл этого отделения третьего уравнения от первых двух сво­дится к тому, что акустические волны давлепия" п ско­рости распространяются независимо от «тепловых» волн
энтропии. Казалось бы, что па этом основании можно было бы вообще ограничиться рассмотрением системы из первых двух уравнений. Однако в общем случае это по так. Дело в том, что при написании краевых усло­вий или при формулировании закономерностей процесса теплоподвода величины bp и bv могут оказаться связан­ными с bs и тогда третье уравнение системы будет играть важную роль.

(4.5)

Система уравнений (4.4) не является, одпако, наибо­лее простои из всех возможных. Действительно, если ввести переменные

И — ciqJSv — f — bp, ] w = aQ0bv — 6p j

И, выразив из этих равенств bv и bp, подставить нх в первые два уравиенЕЯ (4.4), а затем взять почленную сумму и разность полученных уравнений, то система (4.4) принимает следующий вид:

(4.6)

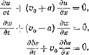
(4.7)

Здесь уже каждое из трех уравнении шисгрируетси отдельно от остальных. При этом все три уравнения совершенно однотипны и поэтому достаточно проинтег­рировать любое из них. Рассмотрим для определенности третье уравнение. Общим решением его является, как известно, выражение

6 s = F(z — o0f),

Где F — произвольная дифференцируемая функция.

Выясним смысл полученного решения. Из паписан — пого выражения впдио, что bs изменяется, вообще говоря, как при изменении ж, так и при изменении t. Однако для моментов времени t п координат удовлетворяю­щих условию

X — v^t = const,

Величина bs будет оставаться постоянной. Пусть для момепта времени t—0 65 есть некоторая заданная функ­ция х. Эту зависимость можно наглядно представить себе в виде мгновенной фотографии некоторой «ВОЛІШ» 6s. Рассмотрим движение «гребня» этой волны (сечения, где 6s имеет наибольшее значение), предположив что этот «гребень» существует. Если в момент времени t=О «гре­бень» пмел координату хи то соответствующее ему сече — иие (т. е. сечение, в котором F достигает максимума) будет перемещаться согласно сказанному выше но закону

Х = хг + V-

Буквальпо то же самое можно сказать п о всех других точках «волны». Следовательно, найденное решение (4.7) описывает движение волны 6s без изменения ее формы в положительном направлении оси х со скоростью

Приведенные здесь формальные выкладки соответ­ствуют совершенно очевидному физическому явлению — поскольку энтропия элементарного объема газа пе может измениться (папомним, что рассматривается идеальная сжимаемая жидкость), то опа будет перемещаться вдоль оси течения вместе с песущпм ее объемом, т. е. со скоро­стью течения.

Совершенно аналогичные рассуждения можпо приме­нить п к первым двум уравнениям системы (4.0) с той лишь разницей, что волны и я w распространяются со скоро­стями v0 — j — а н v0 — а соответственно. Таким образом, волны и движутся только вправо, а волны w только влево. Эти волны могут интерпретироваться как волны акусти­ческих импульсов, движущихся по потоку (со скоростью потока плюс скорость звука) н против потока (со скоро­стью потока минус скорость звука)1).

Введенные чисто формально перемепные и и w пмеют, следовательно, глубокий физический смысл. Правда, в известном смысле эти перемепные менее наглядпы,

Если рассмотреть характер измовевия bp п bv в случаях и ф 0; w — 0 или и=0; w =^0, т. и. при существовании только вол — пи и или только волпы w, то легко полупить соотношение =± Qa 6у. широко известное в акустике для плоской бегущей волны.

Чем б/) и fif, і ex непосредственное измерение при экс­перименте невозможно, однако они оказываются весьма удобными при решении ряда задач. Ниже будут исполь­зованы обе формы записи исходных уравнепий [(4.4) и (4.6)].

Введем систему безразмерных переменных прп ПОМОЩИ следующих равенств:

= t ■

БР _ — _ 6Q _ —_ і ‘ нр0 ‘

— 8» о — —

Єн

1 (4.8)

L ‘ ъ~~ L ‘I Здесь х —показатель адиабаты, a L — некоторый харак­терный ливеннып размер, например длина трубы.

(4.9)

Связь между переменными р, v и и, w, а также $, р и е выражается простыми формулами:

— и —

И = V + р, W = и — р, р = —

$ = р-

Последняя формула приведена здесь для полноты п является следствием четвертого уравнения системы (3.4)- После введсиня безразмерных переменных системы уравнений (4.4) и (4.6) ирп. чут следующий вид:

Здесь Л/ — отношение скорости невозмущонного течения к скорости звука в нем.

Коэффициенты обеих систем зависят только от числа М. Это указывает на существенное значение названного пара­метра в рассматриваемой задаче.

Будем искать решение системы (4.11). Повторив до­словно все то, что было сказано относительно реше­ния системы (4.6), можно утверждать, что трем уравне­ниям (4.11) соответствуют три произвольные волпы И, w н s, движущиеся с безразмерными скоростями (М + 1), (М — 1) и М.

Будем искать частное решение уравнений (4.11), пред­полагая, что произвольная функция F является пока­зательной.

Тогда

И = [і — (М + 1) т] = А. ехр [ р ( т — I) ] ,’ ш = ^[5-(Л/-1)т]=/1шехр[р(т-5^1|)] , (4.12)

Для удобства последующих выкладок в правых частях равенств (4,12) несколько изменена форма записи аргу­ментов.

Числа Аи, Ли., А$ п |3, стоящие в правых частях равенств, остаются пока неопределенными. Здесь следует сделать замечании отпосительио р. Вообще говоря, значе­ния (3 могут быть различными для каждой пз трех пере­менных, поскольку интегрируемая система (4.11) фактиче­ски распалась на трн независимых уравнения. Однако в дальнейшем рассматриваться будут только такие случаи, когда связывающие эти три переменные краевые условия потребуют одинаковых величин р во всех трех показа­тельных функциях.

Проиллюстрируем это примером. Пусть на конце трубы нет колебаний давления (это соответствует обычному краевому условию для открытого копца, если пренебре­гать излучением звука из трубы). Поместив в это конце­вое сечепие начало координат, получим краевое условие р = 0 при £ = 0. Переходя к функциям и, w (4.9), запи­шем это условие в виде и = w прп £ = 0. Теперь иа осно­вании формулы (4.І2) будем иметь:

Аие$х = Awe$x.

Выполнение этого условия для всех т может иметь место лишь при Аи = Аш и одинаковых (5 в левой и правой частях равенства.

Поясним физический смысл величины р. Пусть |3— мнимая величина J3 = iw. Тогда, например, для перемен­ной и можно панисать:

Рассмотрим поведение и в некотором заданном сече­нии | = const, пользуясь действительной частью послед — пего выражения. Легко видеть, что при этих условиях переменная и будет совершать гармонические колебания во времени с частотой

Таким образом, число |3 может иметь смысл частоты колебаний, причем эта частота будет одинакова для всех |. Колебания газа в трубе, происходящие во всех сечениях (при всех І) с одинаковой частотой, должны привести к тому, что все параметры газового течения— давление, скорость, плотность и т. п.— будут колебаться с той же частотой. Последпее обстоятельство является следствием иолучеппого несколько выше формального вывода об оди­наковости р для всех трех показательных функций (4.12), с помощью которых записано изменение различных пара­метров единого газового течения.

Смысл величины [} был выяснен для случая, когда (5 является чисто мнимым числом. В общем случае, когда (5 —величина комплексная, следует по аналогии говорить о комплексной частоте (5. Более подробно рассмотрение этого случая будет дано ниже.

Числа. Ли, .4,у и Ля, являющиеся коэффициентами при показательных функциях в выражениях (4.12), формально определяются следующим образом. Положив х — 0 и | =
получаем а = Лч w = и s — /ls. Следовательно, чпсла Аи, Аи, и /is надо определить как величины и, w и я в начало координат в момент времени т = 0.

Решение системы (4.10), которая эквивалентна только что рассмотренной системе (4.11), можно получить непо­средственно. Однако более простым является использова­ние решений (4.12) п формул _(4.9), связывающих пере­менные р и v с переменными и п W.

Вводя обозначения As н Аи для v tx р в сечении | •= О в момент времени т = О, получим:

+ Л„ ехр ( — ж^гт Pi) J ^ =

= ±[(А+Лр)ех р(-ж11рі) +

Проводел аналогичные преобразования для нахожде­ния р и запишем окончательно частное решение системы (4.10) в следующей форме:

О = [4,фі © + ЛрФ-2 ©]

Где

—Ч-лг^рО]-

(4.13)

(4.14)

4,,(l) = eXp(-ips).

Полученное решение имеет несколько более громоздкий впд, чем (4.12). Однако во многих случаях его можно предпочитать решению (4.12), поскольку оно дает непо­средственные выражения для возмущений основных физиче­ских параметров потока.