В предыдущем параграфе были получены нелинейные соотношения, описывающие процесс вибрационного горе­ния в области а. Ряд упрощений позволил свести нели — пейность к одной квадратичной зависимости. Излагаемый ниже метод пригоден и для более сложных зависимостей, однако уточнение этих иелинениостен вряд ли целесооб­разно здесь, поскольку процесс вибрационного сгорания при больших амплитудах колебаний скорости течения еще очень плохо изучен. В этих условиях всякого рода уточ­нения. которые можно ввести в настоящее время, неиз­бежно были бы перекрыты грубымн предположениями о ха­рактере процесса горения. Поэтому принятая в предыду­щем параграфе идеализация описывает лишь основные, решающие стороны изучаемого явления.

Будем, в отличие от предыдущих глав, решать задачу в переменных (», w) вместо (bp, bv). (Связь между ними дается формулами (4.5).) Переход к переменным (и, w) обусловлен следующими соображениями. Возбуждение колебаний связано, как известно пз предыдущего, с амп­литудой и с фазой bq относительно фазы колебания воз­душных масс. Для того чтобы следить за этими парамет­рами в переменных (bp; dv), пришлось бы одновременно следить как за фазами bp и bv, так и за их амплитудами, поскольку последние изменяются с изменением частоты колебаний (при заданном положении области теплоподво­да о по длине трубы) вследствие изменения стоячих волн bp и bv. Переменные (ы, w) вне зависимости от частоты колебаний имеют постоянные вдоль оси течения ампли­туды, что дает возможность прп решении задачи следить лишь за изменением фазовых соотношений.

В настоящем параграфе рассматривается случай, когда потери на концах трубы отсутствуют. Как уже говорилось, этому соответствуют краевые условия в виде узлов Ьр пли 6v. Примем, для определенности, что система имеет на обоих копцах узлы давления Ьр-=-0. В новых перемен­ных это условие примет вид

(41.1)

Действительно, согласно формулам (4.5)

«? = !(»-»); = <41-2>

Откуда сразу следует условие (41.1).

Пусть начало координат будет совмещено с плоскостью Z (рис. 22), причем введенные переменные будут иметь в этой плоскости значення а0 н ш0. Еслп координата кон­ца трубы равна то, основываясь на выражениях для и и w (4.12) и пользуясь условием (41.1), можно написать следующее равенство:

И0 ехр ( — ш ) = ехр ( — т JJ^ ) .

Б утом равенстве принято, что [3 = г со, т. е. предполо­жено, что колебания установились. Если обозначить фа­зовый сдвиг между ип и w0 через у, то последнее равен­ство дает возможность пайтн его значение

У-жRi»E — (41-3)

Очевидно, что в рассматриваемой задаче надо будет различать два угла у: один, соответствующий левой, другой—правой стороне по­верхности разрыва 2. Отли­чаться они будут тем, что для левой стороны этот угол будет зависеть от величи­ны Ml7 cot и а для пра­вой—от М2, щ и Н2.

Рпс. 82. Схема Отсчета углов на векториой диаграмме вели­чии и и W.

Для того чтобы устано­вить взаимные сдвиги по фа­зам между величинами щ и w0 слова и справа от 2, надо ввести еще одпн угол, например между w0 для ле­вой стороны и и0 для правой. Обозпачпм этот угол через а. Тогда, направив і/0 для ле­вой (холодной) стороны 2 но оси абсцисс, можно будет изобразить векторную диаграмму для и0 н w0, как пока­зано на рис. 82.

Угол а определяется свойствами поверхности 2, ко­торые записаны системой (40.1). Использовав первое уравнение этой, системы и условие изоэнтроппчностп для холодной части течения 6q2 = ~~, исключим 6Qj и 6q3 из двух последних уравнении системы. С помощью формул (41.2) перейдем далее к системе переменных или). Пусть рассматриваемый численный пример характери­зуется следующими данными:

Q, = 0,125 —; ^ ^ 50 м/сек-, pL = 10 000 кг/м*; ‘i = 300° К; 7’,= 1800° К.

Тогда после выполнения вычислений система (40.1) примет следующий вид (здесь илдеь’сы 01 соответствуют левой, а индексы 02 правой стороне плоскости 2):

Ui)2 = 0,583 «01- 0Д75 wol + 0,00289 6g, %vQ2 = — 0,385 w01 + 0,792 w014 0,00603 bg.

Система (41.4) связывает векторные величины. Для перехода к скалярным соотношениям спроектируем эти векторные равенства на оси х и у (рис. 82). Из полу­ченных проектированием четырех равенств исключим cos а и sin а. Учтем далее, что согласно формулам (41.2) при установившихся колебаниях амплитуды и и w не зависят от т. е. на основании принятых краевых усло­вий [ w.011 = | ш01 ] и | іг031 = | ш02 Тогда получим после соответствующих преобразовании следующие скалярные соотношения:

Ы01 (0,583 Cos у2 — 0,175 cos yicos у2 +

+ 0,175 Sin у1 sin у.2 + 0,792 cos Yi + 0,385) = = (0,00603 — 0,00289 cos уа) 6qx — j — 0,00289 sin y2 6g„, a0I (0,583 sin y2 — 0,175 cos уд

— 0,175siny3 cosy2 — 0,792sinyj) = = (0;00603 -0,00289 cos<y2) 6qy — 0,00289 sin ya 6qx.

(41.5)

У величин u0I в последних равенствах опущен знак абсолютной величины, так как выше было введено усло­вие, что вектор м01 всегда паправлен в положительную сторону оси абсцисс. Входящие в правые части величины bqK п 6<7у являются проекциями bq на оси х и у.

Найдем теперь значения bqx ir bq. В рассматривае­мом численном примере постоянная, входящая в формулу

(40.8), равна 2,27 • • Выше уже указывалось, что

В расчет следует ввести лишь первую гармонику раз­ложения функции bq в ряд Фурье, которая определяется равенством (40.9). Воспользовавшись формулой для 6с (41.2), нетрудно найти величину [бс^І, совпадающую по определению с А0 из (40.9):

І=гїк1"»’+і=йі 11+ехр г’Ші щ=і I •

Используя равенство (41.3), полученной формуле можно придать следующий вид:

^=14.1 = ^^2(1+^). (41.6)

Учитывая лишь первую гармонику разложения в ряд Фурье, на основании формул (40.8) н (40.9), (41.6) на­пишем:

6q = 665 ( 5(5 — g-1 1^2 (1 + cosyT) ) gf 1/2(1 + cosyi) •

Здесь б<7 численно равно абсолютной величине j bq |, однако при Av > 56 может и рішим а ть отрицательные зна­чення. Поэтому знак абсолютной величины в левой части равенства опущен.

Фаза bq уя*е была определена выше (относительно бг^): <pi я, т. е. можно считать, что теплоподвод bq колеблет­ся в протпвофазе со скоростью 6i>x. Как следует пз второ­го равенства (41.2), в силу условия |од| = |и| вектор bv будет направлен по биссектрисо угла между и и w, т. е. в соответсгван с рнс. 83 для левой стороны пло­скости 2 будет идти под углом у к осп абсцисс, совпа­
дающей с направлением w01. Угод у[ следует отличать от угла Yr Последний может иметь любую величину, в то время как первый по абсолютному значению

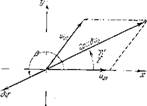
Рис. 83. Определение направлення вектора &<{ при отсутствии потерь л запаздывания.

Не превышает л, так как он используется для построе­ния биссектрисы. Связь между Yi и у! дается очевидным ранепством

У[ = YJ " 2/m> где целое число к выбирается так, чтобы

— я < Y! < я-

С учетом вышесказанного нетрудно видеть, что фазо­вый угол bq относительно будет равен y + jt. Вводн обозначение

Р = я + (41.7)

(41.8)

Получим очевидные выражения для проекций вектора bq на координатные осп:

Bqx = 69 cos р, | bqn = bq sin p. j

> (41.0)

X

В рассматриваемом случае это даст:

= 665^56+cosVl)) X

X-^V"2(iH-cosYl)cos|j,

5qv = 665 (f)() — -^y-] 2(l + cosVl))x

"01

J

X ^]/2(H — cosy,) Sin p.

Подстановка найденных значений 6qx и bqv в систему (41.5) позволяет найти две искомые величины —круговую частоту колебапий и амплитуд иог Этими величинами полностью определяются все параметры колеблющейся системы.

Прежде всего следует указать, что решением системы будет ггП1 = 0 вне зависимости от частоты Одиако это решепие (отсутствие колебаний) интереса не представляет.

Предположив, что и1П ф 0, сократим левые и правые части обоих уравнений (41.5) с учетом формул (41.У) на м01. Тогда система (41.5) стапет линейной, неоднород­ной относительно переменной и01. Величина ы01 легко уединяется в каждом из двух уравнений системы. При­нимая со, за параметр, будем строить кривые и01, в функ­ции col5 по обоим уравнениям. Точки пересечения этих кривых дадут искомые решеппя.

До сих пор делалось предположение, что в зоне горе­ния нет никакого запаздывания. Такое предположение явно пеобоспованпо. Действительно, как процесс распыла горючего форсунками, так и процессы смешения, испа­рения, воспламенения требуют известното времени. Это заназдывапие приведет к тому, что фаза теплоподвода будет сдвинута относительно и01 не на угол Р, а на неко­торый угол Р — j — Поскольку возможные величины запазды­вания неизвестны, будем варьировать fl с тем, чтобы оценить влияние этого фактора на режим установившихся автоколебаний.

На рпс. 84 приведена диаграмма границ устойчивости, построенная на осповании уравпений (40.1) методом, опи­санным в § 19 (область, соответствующая неустойчивости,
заштрихована). Приведенная на рнс. 83 диаграмма пока­зывает, что угол ft, прибавляемый к р для учета явле­ний запаздывания, следует отсчитывать от направления, противоположного направлению вектора 6v. При построе­нии границ устойчивости, изображенных на рис. 84, б?’ было направлено в положительную сторону оси ординат

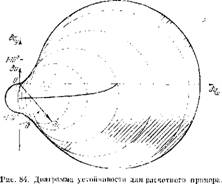
И поэтому угол ft отсчитываете я от отрицательного на­правлення осп ординат. Обозначим через ft’ угол вектора bq с направлением, обратным bv, в предположении вполне определенной ориентация вектора bp (вправо). 11 рп задан­ном угле всегда легко установить взаимное располо­жение 6v и 6р и произвести отсчет угла ft’, который будет либо совпадать с ft, либо отличаться от него зна­ком. При переходе от | бо011 < 56 м/сек к | 6t’011 > 56 м/сек, как это видно из формул (40.8) и (40.9), величина bq меняет знак. Поскольку в методике расчета границ устой­чивости bq может менять знак только путем поворота, для получения угла ft’ при | bvQl j > 56 м/сек к фазе bq следует прибавлять я. Таким образолг, переход от ft к ft’ в зависимости от взаимной орпентпровки 6v и бр следует

Производить по таким формулам:

При 16и01| < 56 м/сек 0′ = ft или ft’ = — ft, при |бо01]> 56 м/сек плп ft’ = я — ft.

При таком правиле отсчета углов ft’ приведенная диаграмма границ устойчивости позволяет ожпдать, что возбуждение колебательной системы будет происходить приблизительно при — 90° < ft’ < 140°.

Подробные расчеты, проведенные по описанной выше методике, подтверждают это. Ниже приводятся результаты таких расчетов. В таблице характеристик автоколебаний, помилю частот to, и амплитуд колебания скорости |6i>01|, удовлетворяющих системе (41.5), даны еще углы ft’. Все три величипы построены в функции угла ft. В таблице прочеркнуты случаи, для которых не существует решенпй системы (41.5), еслп ограничиться первыми тремя гармо­никами. Все расчеты проделаны, для определенности, для среднего положения плоскости 2 по длине трубы: ^=—0,5; !2=0,5. Это положение зоны теплоподвода соответствует используемым ниже опытным данным.

Характеристика автоколебании

Относительно приведенных в таблице решений систе­мы (41.5) надо сделать одно замечание. Полученные здесь решения следовало бы проанализировать с точки зрения устойчивости этих периодических решений, по аналогии с теорией автоколебательных систем, для которых извест­ны устойчпвыо и неустойчивые предельные циклы. Одна­ко такой апализ здесь проводиться пе будет. Вместо этого приведем приближенные качественные соображения, ко­торые позволяют разбить все решения на два типа. К пер­вому типу отнесем решения, дающие |6у01| < 56 м/сек, а ко второму — дающие J6z;01|> 56 м/сек.

Для решений первого тина по мере развития колеба­ний (увеличения 16у01|) вектор 6Q будет первое время направлен в заштрихованную область диаграммы, изо­браженной на рис. 84 (это видно из значений углов О’), И система будет неустойчивой (амплитуды колебаний будут увеличиваться). После перехода через значение |6z?01jj, соответствующее решению, она станет устойчивой; это видно пз того, что дальнейшее увеличение | б vQ1 [ приведет вскоре к измепепию знака AL, т. е. к повороту вектора bq па л, после которого оп будет направлен в пезаштрпховаииую область па рис. 84. Таким образом, решения первого типа дают устойчивые колебания: при I 6t>011 < I bv011/ колебания будут увеличивать свою ампли­туду, при |йу01| > bvQ1T — уменьшать.

Относительно решений второго типа можпо привести аналогичные соображения, которые указывают, что в этом случае устойчивые стационарные колебания невозможны. Действительно, обозначив амплитуду колебания скорости для решения второго типа через |<5у01|//, легко сообра­зить, ЧТО если При I б V01 I = | б У0] |/7 угол ft’ таков, что вектор bq направлен в заштрихованную область на рис. 84, то при | 6у01 | <56 м/сек < 1bv01 п он будет заведомо направлеп в пезаштрпхованную часть диаграммы. Это означает, что амплитуды 6уот будут уменьшаться со временем и авто — I колебания прекратятся. Поэтому решения второго типа | помечены в таблице звездочками и в дальнейшем анализе, учитываться не будут.

Таблица, как и диаграмма границ устойчивости, на­глядно свидетельствует, что величина угла ft (т. е. запаз­дывание) может играть заметную роль. В зависимости от ft будет возбуждаться та илн иная гармонпка, или воз­буждение колебания окажется невозможным. Впрочем, зтот результат был очевиден. Наиболее интересным обстоя­тельством следует признать то, что вне зависимости от величины угла ft в тех случаях, когда происходит само­возбуждение, амплитуду колебаний можно считать прак­тически неизменной. Прп этом величина амплитуды коле­бания скорости несколько превышает среднюю скорость точення уц=50 м/сек. Следовательно, при установившихся автоколебаниях должен наблюдаться периодический за­брос пламени в область перед стабилизатором.

Этот эффект многократно паблюдался в опытах. В част­ности, в специальных опытах, путем установки кварце­вых окон в стенках трубы и скоростной киносъемки процесса вибрационного горепия, удавалось зарегистри­ровать заброс пламени вверх по потоку. В пормалышх режимах горения боковая поверхность стабилизаторов получалась па фотографиях темпой. Прп развившихся автоколебаниях она периодически (с частотой наблюдав­шихся колебаний) закрывалась пламенем, забрасываемым в зону перед стабилизаторами.

Еще более интересно сравнивать амплитуды колеба­ний давления, полученные расчетным путем, с наблюдав­шимися в опыте, поскольку колебания давлення легко измерить. Оценим теоретическое значение амплитуды коле­баний давления в сечении, где расположена пучность давления:

С учетом краевого условия] и = I tv [ ЭТО даст j 6р Ішах— Iи!• Значения

^01 = I ^ I — ^J? (max Для решений первого типа, соответствующих первой, второй п третьей гармоникам колебательной системы, даны в нижеследующей таблице:

Таблица значений ] бр | х «<7-н2

В опытах, которые ставились с целью сравнения теоре­тически полученных величин с экспериментально зареги­стрированными, были реализованы ирпиятые в расчете величины Qt; vQ и т. д. В многократных экспериментах, отличавшихся организацией процесса горения, регистри­ровались амплитуды колебаппя давления перед зоной гореиия. ІІрп развившихся автоколебаниях эти амплитуды имели значения, лежащие между 2200 и 3500 кг/м2. Не­сколько пониженные по сравнению с теоретическим расче­том значения |бі>| объясняются, в частности, тем, что дат­чики давлення не всегда ставились в пучности давления, и, конечно, грубой идеализацией процесса в расчетной схеме.

Однако совпадение расчетных и опытных данных сле­дует признать весьма удовлетворительным. Оно свидетель­ствует о том, что в принятой грубой схеме явлення были учтены наиболее существенные нелппейные свойства зоны теплоподвода.