Анализ характера возмущенного процесса на основа­нии уравнения (31.4) возможен двояким образом. Во-иер — вых, путем рассмотрения числешшх примеров и, во-вто­рых, путем теоретического исследования частных случаев, допускающих аналитическое рассмотрение. В настоящем параграфе будет использована первая из названных воз­можностей.

Найдем по аналогии с расчетами, приведенными в пре­дыдущей главе, границу устойчивости при наличии потерь на концах трубы, т. о. будем искать такие значения 6Х и ЬЕ, при которых колебательная система нейтральна. Будем считать режим течения и положение плоскости подвода тепла заданными (т. е. заданными п, Мг, М2, li и /2), а в качестве переменного параметра выберем часто­ту колебаний оз. Так как по условию v=0 (рассматривает­ся граница устойчивости), то тем самым заданы (для каж­дого ©) все входящие в уравнение (31.4) величины, кроме коэффициентов Сх, Съ С з и С4, зависящих (через аи, ап, я21, а23) от искомых ЬХ и ЬЕ.

Сравнив формулы (17.1) и (31.1), легко видеть, что прп ЬЕ=ухр0 и bX=y. zv0 (где уj и у* — комплексные коэф­фициенты, которые математически выражают существо­вание некоторого механизма обратпой связи):

Рассмотрим для определенности случаи возбуждения колебаний при ЬЕ = 0. При сделанном предположении //i=0 и уравнение (31.4) становится линейным относи­тельно уг соотношением, из которого последняя величина легко определяется.

Результаты такого рода расчета приводятся ниже. Расчет был проведен для двух случаев. В первом анализи­ровалось влияние частоты колебаний па положение гра­ницы устойчивости, во втором — влияние изменения

Относительной длины трубы ~ ^точнее, обратной величи — L

Ны d ) Па ТОї же фактор. В обоих случаях расчет велся для

ЛД=0,15; п= 2,5; т^ 1; ^-^=0,5.

Ь первой серии расчетов, имевшей целью проиллюстри­ровать влияние частоты колебаний на положение границы устойчивости, величина ± была принята равной 0,2, т. е. рассматривалась сравнительно короткая труба, длина которой равнялась 5 .калибрам. Результаты расчета прп — ведены на рис. 61. Здесь по оси абсцисс отложена вещест­венная, а но оси ординат — мнимая часть у2. Комплекс­ный коэффициент у2 дает возможность судить об амплитуд­но-фазовом соотношении между ЬХ и v0. В предыдущей

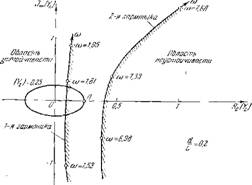
Рін Gi. Іїлііннітс частоты колебаний со на ноложепио границы устойчивости.

Главе п ранее было получено чрезвычайно простое усло­вно самовозбуждения колебапин ігріт отсутствии потерь:

Угол между фазами vQ и б Л" должен быть менее Посколь­ку при bX~y2v„ фазы 6.Y u v0 совпадают при положитель­ных (вещественных) значениях у2, границей устойчиво­сти в рассмотренном ранее примере является мнимая ось, а областью неустойчивости — вся правая полу­плоскость на рис. 61. Как видно из расположения кри­вых у2 на рис. 61, прп учете потерь область неустойчиво­сти уменьшается — границы устойчивости смещаются вправо от мнимой оси и смещаются тем сильнее, чем больше частота колебаний (на диаграмме «неустойчивая» сторона границы устойчивости заштрихована). При этом условие возбуждения усложняется — теперь существенна пе толь­ко фаза ЬХ, но и амплитуда.

Наименьшая относительная амплитуда величины ЬХ (гс условно принято за единицу), прп которой возможно возбуждение, получается тогда, когда фазы ЬХ п и() совпадают (у2 — действительная величина). На рис. 61 приведены лишь две ветви уг (соответствующие первой н второй гармопнкам). Как видно пз диаграммы, увеличе­ние частоты (переход от первой ко второй гармонике) нлечет за собою увеличение абсолютных величин т. е. увеличение относительных амплитуд ЬХ, потребных для возбуждения системы.

Этот результат легко поддается объяснению. Оцепим влияние частоты колебаний на потери акустической эпер­гии в окружающем трубу пространстве. С этой целью воспользуемся выражением (30.7), которое позволяет вычислить поток акустической эпергии, движущейся через концевое сечение трубы. При этом учтем формулу (30.0), позволяющую выразить | £ |2 через вещественную и мнимую части нмпеданца z. Тогда

Полученная формула указывает, в частности, что знак А (направление потока акустической энергии) свя — зап со знаком коэффициента активного сопротивления г. Эта формула может быть упрощепа следующим образом. Заметим, что выражение, стоящее в прямых скобках, близко к единице, так как для рассматриваемых задач величины 7-их малы по сравнению с единицей. Это видно, например, нз приближенной формулы для z (30.8) и*особо подчеркивалось в конце § 30.

Таким образом, для достаточно «длинных» труб и для низких гармоник

(32.2)

Приближенное равенство (32.2) показывает, что поток акустической энергии через концевое сечение Трубы пропорционален квадрату частоты. Следовательно, умеиь — шеиие вероятности возбуждения по мере перехода к выс­шим гармоникам вполне естественно и ход кривых на рис. 61 надо считать типичным. Более высокие частоты дали бы границы устойчивости, еще более сдвипутые вправо.

Иа практике величина г/2 пе может увеличиваться беспредельпо. Реально существующие механизмы обрат­пой связи обусловливают существование верхнего пре­дела этой величины. Если, в частности, верхний предел у. г больше значений, требуемых для возбуждения первой гармоники, ио меньше значений, требуемых для возбу­ждения второй (точка А па рис. 61), то возбуждение колебаний основного тона возможно, а всех более высо­ких гармоник — невозможно. Рассмотренный пример хорошо объясняет то обстоятельство, что в опытах всегда наблюдается возбуждение колебании сравнительно низ — коп частоты.

Оценим порядок у2. Из экспериментов известно, что при развитом процессе вибрационного горения амплитуда колебаний давления бр имеет порядок перепада давления между холодным н горячим газом, т. е. порядок поднора, вызванного тепловым сопротивлением. Этот перепад может быть выражен следующей формулой:

Таким образом,

Переходя к безразмерным переменным и приняв, что в первом приближении —:= — = /?,-, получим:

При развитых колебаниях амплитуда колебаний ско­рости имеет порядок скорости установившегося течения холодного газа и, следовательно,

Порядок величины ЬХ^р.,—рj можно считать совпа­дающим с порядком величии рх її р2. Тогда

І г’і I

Более вероятна меньшая величина у. г, поскольку раз­ность давлений слева и справа от зоны горения обычно составляет не более х12—V3 полной амплитуды коле­баний б р.

В рассмотренном здесь численном примере (гс3 = 6,25; Л/j =0,15) порядок абсолютпой величины у2 будет, таким образом, но более |y2| = 0,25. Сравнивая это значение с абсциссами точек пересечения кривых у2 с веществен­ной осыо (рис. 61), нетрудно прийти к выводу, что в дан­ном случае возможно возбуждение лишь первой гармо­ники системы и то при особеппо благоприятных обстоя­тельствах. Это впдпо из того, что окружность у21=0,25, захватывает лшнь весьма незначительную часть области неустойчивости (прп выбранных на рпс. 61 масштабах эта окружность перешла в эллипс). Такой результат связан с тем, что принятое в расчете отпошение -^ = 0,2 слишком велико. По сути, здесь рассматривается слишком «корот­кая» труба (£.•= 5 с?), для которой относительная величина потерь будет большой.

Это впдно, например, из формулы (32.2), по которой потери растут не только пропорционально квадрату часто­ты, но и пропорциональпо квадрату отноніепня — j — . Следо­вательно, по мере уменьшения ~ количество пзлучасмой

В окружающее пространство акустической энергии должно падать п колебательная система стаповится все более и более склонной к возбуждению. Этим обстоятельством объясняется тот известный экспериментаторам факт, что внбрацпонпое горение можно наблюдать лшнь в достаточ­но «длинных» трубах, т. е. в трубах с малым значением параметра.

Чтобы придать этим качественным соображениям наглядность, па рнс. 62 приведены границы устойчивости для вторых гармоник тон жо колебательной системы, что и рассматривавшаяся выше, по для трех значений пара­метра — j-: 0,2; 0,00 и 0. На приведенной диаграмме хоро-

‘I

Шо видно, что г уменьшением отношении — треоуемая

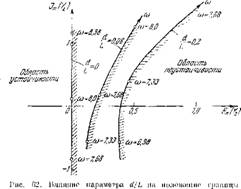
Устойчивости,

Для возбуждения системы величина | //„ ] уменьшается d

И стремится к нулю вместе С — J — .

Экспериментальным подтверждением иолученпых здесь теоретических выводов может служить наблюдение, сде­ланное Киркби и Уилером1). Указанные авторы пишут, что при диаметре трубы 100 мм возбуждение вибрацион­ного горения в пей становилось возможпым лишь при общей длине трубы, превышающей 1400 мм.

Если вернуться к численному примеру и продолжать считать верхпей границей | у2 | значения 0,25, то из рис. 62

!) К і г k b у, Wheeler, Jonrn. of Ни — Llheni. Soc., 1931, стр. 847.

Сдодуот, что при Л с/ ^-^- = 0,06^ вторая гармоника М. ожрт возбудиться, в то время как для -]г—0,2 это невоз­можно.

Приведенный выше пример демпфирующего влияния увеличения частоты колебаний позволяет сделать нагляд­ными те рассуждения о возможпостн препебреженпя начальными условиями, которые приводились в главе II.

Пусть колебательная система имеет те же параметры, что были использованы в численном примере § 23. Един­ственное отличие будет заключаться в том, что потерями на излучение акустической энергии во внешшою среду пренебрегать не будем. На рпс. 33 приведены величины о) п v, полученные для разных гармоник без учета потерь па излучение. Если учесть эти потери, то v п со для первой гармопикп вряд лп изменятся сколько-нибудь заметным образом. Вторая и третья гармоники и без учета потерь на излучение задемнфировапы достаточно сильно (v < 0), учет потерь на пзлучепне лишь усилит это демпфирова­ние. Что касается четвертой гармоники, то без учета потерь на нзлученио она, как и первая гармоника, почти нейтральна. Одпако учет потерь резко изменит это поло­жение, так как частота этой гармоники в 4,5 раза превос­ходит частоту основпого тона, а потери на излучение возрастут, следовательно, в 20 раз. Это соображение позволяет считать все гармоники выше третьей задемтг — фировапными зпачителыю сильнее первой. Будем поэтому в последующих расчетах учитывать лишь три первые гармоники.

Пусть характер процесса в зоне горепия, на основании которого были построены кривые рис. 33, слабо изменит­ся. Пусть указанное слабое изменение произошло так, что первая гармоппка стала нейтральной (v — 0). Что касается второй и третьей гармоник, то сохраним соответ­ствующие им значения v, хотя учет потерь скорее всего увеличит декременты затухания.

Пред ни 11 і, і,чі у,. .1То в начальный момепт т=0 в трубе происходили с.-иысное колебательное движение воздушных масс, составленное нз стоячих волн первых трех гармо­ник, причЄ5г амплитуды второй н третьей гармопик вдвое превышали амплитуды стоячей волны осповпого тона, а фазы всех трех гармоник совпадали. Тогда эпюра мгно­венного значения возмущения р имела бы вид, изобра­женный в верхней части рпс. 03. Вид этой же эпюры в последующие моменты времени т15 т2, т3 дан на том

6’3. Постепенное исчезновение влігшшя на­чальных условий.

Же рисунке ниже. Нетрудно видеть, что уже через время tad2 сохраняются лишь колебания основного тона. Это время соответствует приблизительно 6—7 колебаниям основпого то на. Если учесть, что продольные акустичес­кие колебания, с которыми приходится пметь дело па практике, находятся в пределах 20—1000 герц, то очевид­но, что весь эффект, связанный с начальными условиями, исчезнет за доли секунды-

Приведенная здесь грубая оценка имела целью дать наглядное представление о быстроте, с которой сглажи­вается влияние начальных условий в рассматриваемых системах.