При рассмотрении процесса возбуждения акустических колебаний теилоподводом, которое проводилось в преды­дущей главе, делалось три предположения: считалось, что неподвижная зопа теплоподвода имеет малую протяжен­ность по сравнепию с длішой волпы возбужденных коле­бании, что процесс теплоподвода одномерен и что к про­цессам внутри области теплоподвода применима гипотеза стационарности.

Эти предположения не могут показаться слишком ис­кусственными для таких, например, явлений, как возбуж­дение звука в трубе Рийке при помощи па гретой сетки. Однако, когда рассматривается возбуждение акустических колебаний пламенем, все эти допущения перестают быть очевпдпыми.

Последние два предположения — одномерность про­цесса теплоподвода и гипотеза стационарности — стано­вятся в большинстве случаев просто ошибочными. Что касается первого предположения — малой протяженно­сти зопы теплоподвода,— то им следует пользоваться с известной осторожностью. В силу сказанного, выводы, получепиые в Предыдущей главе, справедливы лпшь для сравнительно узкого класса явлении.

Задачей настоящей главы является разработка схемы расчетной идеализации процессов в зоне горения, свобод­ной от ограничивающих предположении предыдущей гла­вы, и распространение полученных ранее выводов на этот общий случай.

Из всех принятых раньше допущений сохраним лишь одпо — будем считать протяженность зоны горения о ма­лой по сравнению с длиной трубы L (рис. 22). Уточним это предположение в том смысле, что, говоря о малости о, будем пметь в виду не всю область горения, а лишь ту ее часть, в которой происходят заметные колебапия тепло­подвода. Обычно эта зона соответствует начальному участ­ку области горения. Б среднем за период па начальпом

О їг І

Рис. 22. Расчетная идеализация течения в трубе прп наличии подогрева в области а.

Участке может выделяться мало тепла, в то время как коле­бательная составляющая тепловыделения будет сущест­венной. Это естественно, поскольку начальные участки области горения, где горение еще не развилось иолпостью, особенно чувствительны к колебаниям параметров посту­пающей в область го репин топливной смеси. Кроме того, в начальных участках области горения расположен фронт пламени, который может менять свое положение, и т. д. Что касается участков, расположенных па некотором уда­лении от фронта пламенн, в глубине области горения, то хотя здесь н может происходить заметное выделение тепла, колебания теплоподвода значительно менее интенсивны.

Следовательно, говоря и зоне горенпя о, будем всегда пметь в виду, что речь идет лишь о той части области те­плонодвода, которая характеризуется значительными коле­баниями теплоподвода. Остальную часть этой области бу­дем называть зопой догорания, вкладывая в это понятие 8 Б. В. Раушенбах отличный от обычного смысл. В рассматриваемых слу­чаях в зоне догорания может выделяться заметная доля общего количества тепла, подводимого к газу в камере crop а пия.

Итак, будем считать протяженность зоиы о малой по сравнению с общей длиной трубы L, но не будем пренебре­гать нсстационарностыо п объемным (трехмерным) ха­рактером происходящих в ней процессов. Что касается участков Lx и £2, лежащих слева и справа от <г, то будем продолжать считать, что процесс распространения возму­щений в них одномерен и описывается выражениями, полученными во второй главе. Добавим лишь, что вдоль участка L2 (горячий газ) вследствие догорания фактиче­ски могут изменяться температура и средняя скорость течения.

Чтобы пользоваться простыми формулами второй гла­вы, будем осреднять температуру и скорость течения по участку Ь2. Как показывает оценка, это ие может сущест­венно сказаться на результатах расчетов.

При аналитическом исследовании акустических коле­баний в трубе принятая схема явления создает значитель­ные трудности. В осиове этих трудностей лежит то, что на участках Ll и Ь2 процесс одномерен и описывается уравне­ниями акустики, в то время как внутри короткой зоны а приходится учитывать трехмерность процесса горения и целый ряд сложных физических и химических законо­мерностей, свойственных горению. Зона а не только делит все течение на два участка, по и существенно изменяет характер акустических возмущений в областях, лежащих слева и справа от пее.

Наглядиое представление об этой роли зоны а можно получить, рассматривая движение некоторого единичного акустического импульса вдоль трубы L. Пусть такой им­пульс движется по участку Ьх вправо. Достигнув зоиы а и встуипв во взаимодействие с процессом горения, рассма­триваемый импульс частпчпо отразится и двинется влево по участку Lx, а частично пройдет через зону а. Однако импульс, вошедший в участок £2, будет отличаться по фа­зе и амплитуде от породившего его импульса.

Как видно из сказанного здесь, зона а является обла­стью, в которой происходит трансформация акустических возмущений. Еслп характер этой трансформации почему — либо заранее пзвестен, то расчет можно вести, непосред­ственно связывая акустические возмущения па граничных плоскостях Fx н F2 (см. рве. 22) п не интересуясь деталями явлений, происходящих внутри а. Чтобы пе внести при этом искажений в акустические свойства системы, завися­щие от общей длины трубы L, можно соответственно удли­нить участки Ьх и L2. Это рассуждение приводит к расчет — нон схеме, изображенной в нижней час-тн рис. 22. Вся труба делится на две части не короткой зоной а, а плоско­стью 2. Возмущения течения на левой стороне плоскости 2 совпадают с возмущениями па Fly а возмущения на правой стороне плоскости 2 с соответствующими величинами на FПоскольку амплитуды и фазы одноимепных возмуще­ния па Fx и F2, вообще говоря, пе совпадают, фиктивной плоскости 2 падо приписать свойства поверхности силь­ного разрыва газодинамических параметров течения. При такой идеализации процессов в трубе онп будут всю­ду одномерными и будут подчиняться акустическим зако­номерностям. Свойства же плоскости 2 еще подлежат определению. Не надо думать, что введение плоскости 2 вместо зоны о спльпо искажает всю картипу явлепия, по­скольку достаточно сложный процесс сгорания, происхо­дящий в некотором объеме, заменяется мгновенным под­водом тепла на плоскости 2. Солее правильным будет иное представление. Зопа а как бы «извлекается» из течения и подробно изучается отдельно. Когда же свойства ее ясны, т. е. ясна связь между параметрами на Fx u F2, то этп свойства формально приписываются левой и правой стороне плоскости 2.

Вводя вместо реальиой зоны горения а поверхность сильного разрыва’ 2, следует, конечно, наделнть эту по­верхность всемп существенными свойствами зоны тепло­подвода а. Введение поверхности разрыва вместо протя­женной зоны теплоподвода является приемом, который использовался почтп всеми авторами, занимавшимися изучением процесса термического возбуждения звука. Что касается свойств введенной поверхности 2, то обычно онп формулировались неточно, что искажало результаты исследования. Дадим поэтому строгий вывод свойств, которые следует приписать поверхности 2, а для этого найдем связь между параметрами течения на плоскостях [< и Г2.

Прежде всего определим границы области сг. Будем называть зоной горения некоторый объем V, заключенный между двумя неподвижным н плоскостями, нормальными к оси трубы, впутри которого происходит процесс горения. При этом длина зоиы горения сг должна быть взята с уче­том не только возможной криволинейности фронта пламе­ни, но и с учетом колебаний фронта во времени — поверх­ность пламени не должна пересекать границ объема V пи в одном из своих положении.

Поскольку за пределами зоны горения V процесс при­нимается одномерный!, такое же предположение следует сделать относительно характера течения в сечениях, огра­ничивающих объем V. Поэтому зона горения может иметь несколько большую протяженность, чем расстояние меж­ду крайними положениями поверхности пламени, дости­гаемыми в результате колебаний.

Как было показано во второй главе, процесс распро­странения возмущений описывается тремя переменными, зависящими от коордипаты п времени. Поэтому для «склеи­вания» распространяющихся слева и справа от зоны горе­ния возмущений необходимо пайти три независимые свя­зи между возмущениями слева и справа от V. Для форму­лирования этих связей целесообразно применить законы сохранения. Воспользуемся уравнениями потоков массы, импульса и энергии в тон форме, в которой они приведены в курсе J1. Ландау и Е. Лифшица1), дополнив эти уравне­ния рядом иовых членов.

Во-первых, уравнение потока энергии следует писать с учетом химической энергия, переносимой течением. Здесь под этим понимается скрытая химическая энергия единицы массы горючей смеси д. Изменение величины q при пересечении зоны ст говорит о том, что часть этой энергии перешла в тепловую форму в результате процесса горения.

Во-вторых, в зоне теплоподвода а могут быть располо­жены источники массы, импульса или энергии. Источник

*) Л. Л а и Д а у и Е. Л и ф ш и ц, Механика сплоппгах сред, Гостехиздат, 1953 г.

Массы может существовать, например, в виде системы фор­сунок, подающих горючее, еслп эти форсунки расположены пе перед зоной горения, а внутри нее. Однако обычно го­рючая смесь готовится перед зоной горения, и поэтому реальный источник массы в зоне а отсутствует. Даже в тех случаях, когда в попе горения оказывается источник мас­сы такого тпна, им обычно можно пренебрегать. Поэтому, написав для общности соответствующее слагаемое М’ п уравнении потока массы, в дальпейіпем в настоящей кни­ге будем почти всюду полагать М’= 0. Чтобы это утвер­ждение не вызвало недоумения, укажем, что условие М’ = 0 достаточно хорошо отражает процессы сжигания горючего в воздухе. В случае анализа работы жидкостных реактивных двигателей полагать М’~ 0 было бы певерно. В теории жидкостных реактивных двигателей принято пре­небрегать объемом, занимаемым топливом, находящимся в жпдкой фазе. Поэтому папболее естественной идеализа­цией процесса горения в таких двигателях является сле­дующая схема. Каплн тонлпва движутся но газовой среде до некоторого сеченпя камеры сгорания, где они мгновен­но превращаются в газ (сгорают). Следовательно, в этом сечении находится мощный источник газов (источник мас­сы). Это аналогично случаю, когда форсуіши, подающие горючее в воздух, находятся в зоне горения, но в отлпчпе от этого случая в жидкостных реактивных двигателях че­рез форсунки подается не малая доля массы, поступающей в зону горения, а вся эта масса. Поскольку подробный ана­лиз работы жидкостных реактивных двигателей не являет­ся целью настоящего исследования, всюду (кроме соответ­ствующего параграфа гл. X) будет предполагаться что ЛГ= 0.

Относительно источника импульса, расположенного внутри зоны о, можно сделать следующие замечания. На­личие такого источника является вполне вероятным. Его можно представить себе в виде некоторого сопротивления І5′, которое оказывают потоку различного рода конструк­тивные элементы (например, стабилизаторы), находящиеся

«

Амере сгорания. Так как аэродинамические силы, нри — кенные к этим конструктивным элементам, по со верша — внешней работы, можпо сказать, что такой источник импульса не является источником энергии (сопротивления только изменяют соотношение между количествами меха­нической и тепловой энергии, переносимых потоком, но не меняют их суммы).

Что касается источника тепловой энергии Qкоторый учитывается при написании уравнения потока энергии, то условимся понимать под ним теилолодвод, пе связанный с гореиием, напрИАіер, теплоподвод от нагретых сеток втру — бе Рийке ИТ. н., либо теплоподвод от горючего, введенного непосредственно в объем V, минуя его границы.

Условимся также не делать в дальнейшем различия между понятиями «источник» и «сток» (последний будем рассматривать как отрицательный источник).

С учетом сделанных выше замечаний законы сохранения массы, импульса п энергии могут быть записаны в следую­щем виде:

§Qvdf=-Ј[iQdV + M’,

V

V

§Q"(j + с"т + 0 df= — — ж е ( g)dV+Q’.

V

(15.1)

Здесь вектор df, соответствующий элементарной пло­щадке df поверхности, ограничивающей объем V, па прав­лен по внешней нормали к этой поверхности, а тензор нлотпости потока импульса определяется выражением

Где — единичный тензор. Стоящие в левых частях равенств (15-1) интегралы берутся по неподвижной по­верхности, ограничивающей зону горения V.

Обычпо эти интегралы по поверхности вычисляются легко. Пусть ось потока совпадает с осыо а зона горе — иия будет цилиндрической, вырезанной из общего объема неподвижными плоскостями Fx и F2 (см. рис. 22). По оговоренному выше условию течение в сечениях 7*1 и Рг является одномерным. Следовательно, па поверхностях, ограничивающих объем V (плоскости Fx и F2 и боковая поверхность цилиндра), единственной компонентой ско­рости, отличной от нуля, будет vx. Но тогда интегралы но ограничивающей область V поверхности сведутся к разности интегралов по плоскостям Р и Fr

Вводя индексы «единица» для параметров потока па 1< (холодный поток) и индексы «два» для параметров потока на F2 (горячий поток), получим с учетом того, что в силу принятой цилилдричности зоны горения пло­щади сечения Fx н Fz равны между собой:

V

V

Є2^2 (_ у + ciA + ?а ) = QLVI ( Vf + Срі Л + Я і) —

Где

РІ

-F —площадь поперечного сеченпя камеры.

В общем случае, $ силу неполноты процесса сгора­ния, q2 Ф 0. Введем понятно мгновенной эффективной полноты сгорания

= (15.3)

Нетрудно впдеть, что прп стационарном процессе или при У = 0 введенное определение т)сг совпадает с обще­принятым определением полноты сгорания.

При пестацпопарпом горении выражение (15.3) пе имеет такого простого физического смысла, так как сго­ревшая порция топливной смеси, пересекающая плоскость F^, могла иметь до сгорания (вследствие колебания q) другую теплотворную способность, чем смесь, пересе­кающая в это мгповенио плоскость Fv

Воспользовавшись формулой (15.3) и первым равен­ством (15.2), последнему равенству системы (15.2) можно придать следующий вид:

02^2 (х + W ) = ЄІ^І (д + <4 ті + Чсг ^ ) +

V V

(15.4)

(здесь jҐ* = 0).

Следуя принятому методу, проведем линеаризацию полученной системы уравнении. В результате будем иметь:

Є2в»г + игбра = р^И! + w,6gi — y^fj — QdV + ЬМ*,

V

+WJ6 Qj+ вр, = гріИ, + б/J,—

V

(д Єг«.2 + Q2ci>2 ‘l + Й2?г ) +

Л (15.5)

+ <у-І+ + ЩЧг ) + ч ч-рф’1 г +

— QA&q-i = ( 4 + Є А-./, 4- Є.’/j ) ви, —

+ (т + + )бЄі + с*іЄі"1-»1 + А/. — r IF [6 (т + c»r+«)dV+6l?*-

V

Lie л и наїттісать последнее уравнение системы (15.2) в форме (15.4), то соответствующее уравнение системы

(15-5) примет вид: ‘

(уе2и? + ) Ьц, + ("j + afe + чвлвг, =

= ( у Рі»? + Єї СР,’l + Єі’ісг <7і ) б^ + + (у + "Л’, т 1 + "ііи — <7і) Й01 + + ел 6Т1 + Qiiyicr + ел?! бііог +

(1 ■^-Ь) y| Єdv-Ц + crT — И)^ + bQ*.

V V

(15.6)

Воспользовавшись соотношениями (4.8), приводом систему уравнений (15.5) к безразмерному виду, причем в первом уравнении положим ЬМ* = 0, а последнее уравнение этой системы запишем в форме (15.6). Учиты­вая то, что согласно равенству (4.9) s = /? — q и что для невозмущепного течения стоящпе в правых частях ра­венств (15.2) частные производные ио времени от интег­ралов обращаются в нули, получим следующую систему ‘):

= | [ + ( мл + ± YPl M[sx + Mvr2 + М, П ]

+ (15.7)

+ С лу! + + <?0 — W — і — ‘Л) f

+ <>1 (%Г + 4- Ja f 2Af*Q* ] .

3) Чтобы упростить записі, системы, здесь и всюду далее не делается разницы между их и х2—показателями адиабаты в хо­лодном я горячем газе. При желании это всегда легко учесть.

Здесь

Q __ 2тісг<?і — _вчср — б?,

VI — .2 > 1ог — ^ . (ll ~7. 1

И1 ^СГ ‘II

Ъ» _ ІРІ 7J. 6(2*

Ъ — шЦоЧГ,

V

V

У

В паиисанных формулах vv і]сг и дг соответствуют невозмущепному процессу; никаких дополнительных индексов для обозначения параметров стационарного течения здесь не используется.

Слагаемые Р* и Q* в системе (15.7), как правпло, будем опускать, так как первое из них не играет замет­ной роли в процессе вибрационного горения, а второе (соответствующее теплоподводу, не связанному с пересе­чением горючим границ области У) проявляется лишь в специальных случаях (возбуждение колебаний нагре­тыми сетками, введение горючего непосредственно в зону сгорания).

Входящая в третье уравнение системы (15.7) величина

_ 2г|сі>(7і « /-

Qi = —— но является независимой. Уна полностью опре­деляется заданием параметров течеппя слева и справа от о. Для установившегося потока третьему уравнению системы (15.2) при Q* = 0 можно придать следующий вид:

Єї т + ІГ=Ї № + QlVi = + Й

После делеиия обеих частей равенства на Щ1, с уче­том того, что = , сразу получаем ^

Ft == {мі + jA.) — (м;+. (15.9)

Величина и = — может быть (при Р* = 0 и М* = 0) най­дена из первых уравнений (15.2) для установившегося потока:

(15.10)

■лМъ 1 2

Таким образом, пользуясь формулами (15.9) п (15.10), можпо представить все коэффициенты системы (15.7) в функ­ции Мг и М% — чисел Маха стационарного точения слева п справа от о.

Система уравпеинн (15.7), так же как и исходная систе­ма (15.1), справедлива не только для зоны горения малой протяженности, но и для любого, сколь угодно большого участка течения. Введенное выше предположение о малой протяженности зоны горения оказывается существенным нз следующих соображений. Как уже говорилось, в певоз — мущеппом течении J1=J2=Js:=0. В возмущенном течении эти величины, вообще говоря, отлнчны от нуля и зависят от распределения по рассматриваемому объему V возмуще­ний q, v п Т. Возмущения указанных иараметров могут быть связаны как с акустическими процессами, так и с процессом горения. Еслп доля первых пренебрежимо мала, то величины Jv J. z u J3 в ураввеппях (15.7) зависят только от процесса горенпя. Это обстоятельство чрезвы­чайно существенно, так как лишь в этом последнем случае можно провести мысленную операцию «извлечения» зоны а пз трубы L, нужную для того, чтобы связать между собою параметры течепня на границах о. Ведь эта связь должна быть одинаковой для всех видов акустических возмуще­ний, для всех частот, которые определяются (в зависимо­сти от свойств участков и L2) лишь после того, как свой­ства зоны а уже сформулированы.

. Следовательно, малую протяженность зопы. ст надо по­нимать как малую протяженность но. сравнению, с длинами волн акустических возмущений. Принятый здесь прием идеализации перестает быть справедливым для очень ко­ротких волн, соответствующих высоким гармоникам. Одна­ко это обстоятельство не ограничивает существеиио при­менимость развиваемого метода, поскольку высокие гар­моники обычио пе возбуждаются.

В тех случаях, когда зона теплоподвода, в которой про­исходят значительные колебания тепловыделения, велика но сравнению с длиной волпы возмущения, можпо ввести несколько поверхностен разрывов 2, соответствующих долям зоны а и отстоящим на должных расстояниях друг от друга. Такой же прием примепим и в случае, когда коле­бания тепловыделения имеют место не в одной короткой зоне, а в двух или трех, удаленных на заметное расстояние друг от друга.

§ 16. Свойства плоскости теплоподвода 2

Очевидно, что существенные для возбуждепия акусти­ческих колебаний свойства плоскости 2 и зоны а должны совпадать. Эти свойства записаны выше в виде системы (15.7), связывающей параметры течения и, р и s па двух, сторонах поверхности сильпого разрыва 2. Глядя па си­стему равепств (15.7), петрудно убедиться, что вводимая вместо зоны ст фиктпвпая поверхность спльпого разрыва 2 обладает особыми качествами.

Особенностью этой поверхности разрыва является то, что во всех трех уравнениях, описывающих ее свойства, пар яду с переменными р, v, s фигурируют величины /15 /2 и /3, Qt, г|сг и qv Если вспомнить, что первое из урав­нений (15.7) является выражением закона сохранения мас­сы, второе — закопа сохранения импульса, а третье — закона сохранения энергии, то следует принять, что на по­верхности разрыва 2 расположены источники массы, им­пульса и энергии, даже в случае М* = Р% = О* — 0.

Действительно, поскольку зона ст сведена к плоскости 2, величины /lt /2 и Jz уже нельзя трактовать как произ­водные от интегралов по объему V, ибо этот объем равен нулю; нх следует рассматривать в качестве интенсивпостей источников, расположенных па 2.

Тогда уравнение неразрывности примет вид

Если учесть, что в схеме течопия с поверхностью разры­ва 2 qj и I?! относятся к левой стороне поверхности, a qa и Vn к ее правой стороне, то величина J может рассматри­ваться только как интенсивность источника массы, распо­ложенного на 2. Совершенно аналогичные рассуждения можно провести и для двух других уравпенин.

Следовательно, хотя внутри зоны горения источники массы и импульса могут фактически отсутствовать, их при­ходится вводить для фиктивной поверхности разрыва 2, чтобы сохранить существенные свойства этой зоны. Харак­тер этих фиктивных псточников /ц /2 и /доднозиачио определяется формулами (15.8), т. с. реальным процессом внутри объема зоны горения V.

Таким образом, зону горения малой протяженности, со сколь угодно сложным процессом внутри пее, всегда можно заменить неподвижной поверхностью сильпого раз­рыва 2 при условии, что на этой поверхности будут рас­положены фиктивные источшшп массы, импульса и энер­гии цужпой интенсивности Легко видеть, что при этом будут охвачены все возможные виды колебаний в трубе. Действительно, задавая произвольным образом значения v, р и $ но обе стороны 2, можно, как это видно из системы (15.7), связать их без нарушения трех осповпых законов сохраиения, путем выбора соответствующих значений без­размерных интенсивностей источников массы, импульса и энергии.

Это становится наиболее понятным, если обратиться’ к исходной системе уравнений, записанной в впде (15.2). Обозначим

Необходимо сделать следующие замечания. Составляю­щие всех источников делятся на фиктивные и реальные слагаемые. Как уже говорилось, реальным источником массы может быть горючее, вводимое в зоне горения
в воздушный поток, а реальным источником импульса — со­противление стабилизаторов, форкамер и пных устройств, которые могут быть расположены в зоне горения. Одпако обычно этими составляющими можпо пренебрегать. Поэто­му во многих случаях в этой книге говорится, что в зоне теплонодвода отсутствуют реальные источники массы и импульса.

Относительно источников эпергии этого сказать нель­зя — процесс горения дает мощный реальный источник теплоты. Рассмотрим поэтому поток тепловой энергии, по­рожденный источниками, расположенными внутри обла­сти а более подробно. Его можпо разбить па реальную п фиктивпую составляющие. Если ограничиться лишь воз­мущениями потока энергии, то к реальной составляющей следует отнести 2MQ* — возмущепие теплоподвода, не связанного с пересечением горючим границ области сго­рания, сумму Qx 4" Pi — возмущение теплопод­вода, обусловленное изменением массы горючей смеси, поступающей в зону горения через ее границы, н (rjcr + <7i) — возмущение теплоподвода вследствие коле — бапия полноты сгорания и теплотвориой способности горючей смеси. Все эти составляющие можно объединить, написав

Q = 2MQ* + Ql (Л — v, + Jh — 7t) + Q, (nor+ g,). (16.1)

Слагаемое 2MJa в уравнении (15.7) дает фиктивный источник эпергии (подобпо тому как Jx и J2 — фиктивные источники массы и импульса), который вводится лишь для того, чтобы сохранить существенные свойства протяженной зопы горения после сведения ее к поверхности разрыва 2. Прн этом следует иметь в виду, что, в отличие от Q, энер­гия, связанная с фиктивной составляющей /8, может иметь не только тепловую, но и механическую или хими­ческую форму, что следует, в частпости, пз выражения для J3 (15.8).

Сделаем еще одно почти очевидное замечание. В поня­тие «нсточник энергии» здесь вкладывается пной смысл, чем в предыдущей главе, в которой исследовались источ — иики энергии, питающие автоколебательную систему. Здесь речь идет о подводе энергии к газу в зоне теплоподво­да, независимо от того, тратится эта энергия па возбужде­ние акустических колебаний, на пагрев нли еще каким-ли­бо образом. Кроме того, как видпо из формул для Q и У8, речь идет лишь о перомсппой во времени составляющей источника энергии. Последнее нужно всегда иметь в виду, поскольку в зоне горепня существует значительная посто­янная во времепп составляющая теплоподвода.

Таким образом, заменяя реальную зону горения а поверхностью сильного разрыва 2, следует приписать по­следней ту же величину безразмерного возмущения внеш — пего теплоподвода Q, которая свойственна зопе а (Р* пола­гаем пренебрежимо малым) н, кроме того, считать, что па поверхности 2 расположены фиктивные источпики мас­сы, импульса и эпергии с безразмерными інтенсивностями

Уц У2 и У8. _ _ _

Физический смысл величии Jv У2 и У3 достаточно оче­виден Рассмотрим, например, Ух. Поскольку зопа горения фактически обладает известпой протяженностью, и по­скольку положение фронта пламени в пей может изме­няться, количество горячих и холодных газов в этой зопе пе будет неизменным. Следовательно, мгновенные значе­ния расходов массы на входе в зону горения и па выходе пз нее могут не соппадать, хотя прн установившихся колебаниях в средпем за цикл они совпадут. Это эквива­лентно существованию фиктивпых источников массы на плоскости 2 с колеблющимся расходом, в средпем (за цикл) равным нулю. Совершенно аналогичные рассужде­ния можно провести и для У2 и У3. Здесь также могут коле­баться количества импульса и энергии, заключенные в объеме У, и при сведёппи объема У к плоскости 2 это ведет к необходимости считать, что па 2 расположены фиктив­ные источники импульса и энергии со средним (за цикл) расходом, равпым нулю.

Входящие в систему уравнений (15.7) величины Q, РІ, У і, Уг> Л» которые характеризуют процесс нестационар­ного теплоподвода, могут быть определены лишь после того, как будет задана картипа процесса внутрп зоны горе­ния. Это составляет обычно главную трудность и требует постановки целой серпп тонких экспериментов, например скоростной киносъемки зопы горения с одновременной безынерционной записью колебаний параметров газового течения. Иногда принимается та или иная теоретическая схема процесса колебательного горения, которую надо изучать; в этом случае определение всех необходимых ве­личин по формулам (15.8) оказывается более простым.

Рассмотрим ряд простейших случаев, которые позволят проиллюстрировать использование формул, получепных в предыдущем параграфе, п помимо этого выявить некото­рые пптересные свойства зоны теплоподвода. Прежде всего обратимся к двум предельным случаям, которые позволят обратить виимание на одно принципиально важное об­стоятельство. Исследуем, с одной стороны, подвод тепла при пересечении потоком неподвижной плоскости, нормаль­ной к оси течения, и с другой — подвод тепла прп пере­сечении бесконечно тонкого фронта пламени, также нормального к оси течения, но свободно колеблющегося вместе с потоком.

Подвод тепла на неподвижной плоскости. Этому слу­чаю соответствует возбуждение колебаний в трубе Ринке, поскольку в идеализированной схеме нагретую сетку мож­но представить в качестве неподвижной относительно сте­нок трубы плоскости, при прохождении через которую воздушный ноток нагревается. Для камер сгорания такому случаю в какой-то мере отвечает густое расположение под­жигающих источников в одной плоскости нормального сечения камеры, хотя здесь степепь приближения идеали­зированной схемы к реальному процессу уже будет меньшей.

Особенностью рассматриваемого процесса является то, что объем зоны горения (или, в более общем случае, зоны теплоподвода) равен пулю. При этом, очевидно, /1 = /2 = = /3 = 0, и на вводимой в расчет поверхности 2 будет располагаться только источник энергии, дающий возму­щенную составляющую внешнего тенлоподвода Q. Прп горении возбуждение колебаний возможно за счет вариа­ции полноты сгорания г|сг и теплотворной способности c-Aiocu дх1]. Более подробно этот случай будет рассмотрен’ и следующей главе.

Для трубхл Рийке в уравнение энергии войдет вели­чина Q*, зависящая от теплоотдачи от сотки к воздуху.

Подвод тепла в плоском фронте пламени. Пусть фронт пламени, как уже указывалось выше, пормален к оси трубы и не закреплен относительно ее стенок. В установившемся режиме неподвижность поверхности

Пламени относительно стенок достигается тем, что ско­рость потока смеси в трубе численно равна скорости распространения пламени. Предположим, что горючая смесь гомогенна и имеет всюду одппаковый состав, а ирод ее с сгорания в бесконечно тонком фронте пламени происходит мгновенно п всегда с одинаковой полнотой, например, т|сг = 1. Очевидно, что в этом случае возмуще­ния 1-1^ = 7] = 0, и возбуждепис системы будет связано с величинами 71? /2 и /3, отличными, вообще говоря, от нуля вследствие — подвижности фронта пламени.

Для вычисления величии /2 и /3 обратимся к рис. 23, па котором приведена схема горения для рассматрпвае-

Слагаемое ^ , входящеев Q, интереса до

Продетавяяет, так как одо однозначно связало с д и и по может свободно варьироваться как, папрішер, т]сг и 9 б. В. РаушенОах

Мого случая. Плоский фронт пламени Л колеблется между неподвижными сечениямн и причем скорость, плотпость п другие параметры перед и за зоной горения равны соответственно v1 + &v1, gj + 6g, и т. д.; в, + вва, + и т. д. Поэтому

Где — мгновенное значение «холодного» объема зоны горения (от Fi до A), Fr — мгновенное значение «горячего» объема зоны горения (от А до Fz).

В силу того, что рассматриваются малые колебания, величина а имеет порядок возмущении. Такой же поря­док будут иметь и связанные с нею объемы Fx и Fr. Очевидно, слагаемыми 6qj и 6q2 под знаками интегралов можпо пренебречь. Из геометрических соображений ясно, что изменения Fx и Fr равны н противоположны по знаку:

■И

Vx v,,

Следовательно,

(16.2)

Буквально те же рассуждения следует применить и при вычислении /2 и /3. При этом в силу того, что для стационарного течения рассматриваемого типа урав — непие неразрывности имеет вид Qifj = величина /2 оказывается равной пулю.

Єї (■у-гсі’Л+?і’) — 6г ‘■утСі-г’з+Зг"4!—<7і(1—Чсг)(ві—ег)

QSF x

X-^VAt). (13.4)

Входящая во все три полученные выражения величина 1 д

— — FP (t) является, лак нетрудно сообразить, мгновен — пьш значением скорости распространения пламени отно­сительно стенок трубы N. Поскольку положительное направление оси х совпадает с направлением скорости установившегося течения, можпо написать

Л^-тг-^-ЫО — (1Є-5)

Обозпачим скорость распространения пламени относи­тельно частиц газа через U. Заметим при этом, что введеішая скорость U чпслеішо совпадает с обычно при­меняемой в теории горения скоростью распространении фронта пламени £/сгор, отличаясь от пее знаком. Дей­ствительно, прп используемом направлении оси х поло­жительным значениям U соответствует движение вправо, в сторону горячих газов. Таким образом, скорость рас­пространения пламени Ucrop, которая направлена в сто­рону холодпых газов, должна в принятых обозначениях соответствовать U < 0. Ниже будет почти всюду исполь­зоваться скорость U, однако все выводы легко сформу­лировать п для £/сгор.

Запишем теперь очевидное кинематическое соотношение o-i-U = N. (16.(і)

Тогда bv -1- ЬС7 = 6.V, по так как в установившемся режиме iV = 0, то bN совпадает с А’. Это позволяет за­писать равенство (16-6) в таком виде:

Б V + bU = N. (16.7)

Приведя последнее соотношение к безразмерному виду путем деления на скорость звука в холодном потоке av можпо на основании фор, мул (16.2) —(16.5) и (16.7) на­писать следующие выражения для Jv J,2 и /3:

7,-Мъ + и,), ,

J, = 0, (16.8)

73 = Js (», + ;?,). ‘

„ JT ю,

•Здесь t/, = — — оезразмерное возмущение скорости рас­пространения пламени относительно холодпого газа, а численные коэффициенты А1 и Л3 находятся по

А*

Формулам:

К (к— 1) Ml J

1

)- > (16.9)

1

■ лг^Л J і ^ ма J J

—1 )М

Сравним теперь два рассмотренных, случая. Нетрудно видеть, что опп отличаются принципиально. В первом случае возбуждение колебаний возможно за счет возму­щения внешнего теплоподвода Q, а во втором — за счет возмущения скорости распространения иламенп Ux. Воз­никает естественный вопрос, нельзя ли свести любой эффект возмущения скорости распространения пламени Uх к некоторому эквивалентному случаю возмущения внеш­него теплоподвода Q? Ответ па этот вопрос может быть только отрицательным: в то время как колеблющееся тепловыделение, происходящее па пеподвнжной плоскости теплоподвода, дает отличное от нуля слагаемое лишь в третьем (энергетическом) уравнении систем (15.7), под­вижность пламени приводит к появлению отлпчных от нуля слагаемых и в других уравнениях [в рассмотренном случае 1гФ О и /3 ф 0]. Поэтому принципиально невоз­можно заменить эффект колеблющегося пламени некото­рым эквивалентным колеблющимся тепловыделением на неподвижной плоскости нодвода тепла. Здесь можно при­вести такое простое соображение, иллюстрирующее бес — •еерснективпость попыток найти эквивалентные возмуще­ния тепловыделения при произвольном процессе в зоне горения. Пусть будут заданы возмущения р, v н s по обе стороны зоны горения. Для того чтобы связать пх без нарушения трех законов сохранения, нужны три свободных независимых параметра, например Jx, J2 и QJr2MJz. В то же время такую связь невозможно, вообще говоря, установить, располагая одним парамет­ром Q. Этот вопрос почти очевиден п подчеркиваете я здесь лишь потому, что нзвестігьі многочисленные попытки сводить все нестационарные процессы горенпя к некото-
рому эффективному колебанию тепловыделения, что почти всегда связано с нарушением законов сохранения массы и импульса.

Подвод тепла во фронте пламени произвольной кон­фигурации. В качестве третьего случая рассмотрим под­вод тепла во фронте иламепи А произвольной конфигу­рации, отличающемся тем, что он является непрерывной, бесконечно топкой поверхно­стью, отделяющей в однород­ной горючей смеси горячий газ от холодного (рпс. 24). Пусть фроит пламени А со­вершает колебания между сечениями Fx и Fz, непрерыв­но меняя свою конфигура- Рис. 24. К определению эф — цшо. Если предположить,- фек-гивной скорости распро-

Чтп г vtttppтмокяттіго псктшн — стране(шя пламени при пропз- существование искрив вояьпой конфигурации фронта

Ленного фронта А не влияет иламеаи.

На течение перед ним, полно­та сгорания всегда одна и та же, а за фронтом пламени плотность, давление и скорость всюду равпы соответ­ствующим параметрам точения в сечении F2Х), то все выводы, сделанные із предыдущем пункте, сохраняют свою сплу. Единственным различием будет то, что вели — 13

Чина — — р — Vr (і) не оудет оольше мгновенной скорости распространения пламени относительно стенок трубы. Однако по аналогии с предыдущим можно обозначить это выражение уУдфф и называть его эффективной скоростью движения фронта иламепи относительно стенок. Соответ­ственно п величина U может быть заменена на 6Г13фф =

= А^афф-— х)у ^где ДгЭфф = —и названа эффективной скоростью распространения пламени относительно холод­ного газа. С введением этих понятии задача сразу сво­дится!? формулам (16.8), в которых Ux заменяется на 771 эфф.

Эти предположения следует признать довольно грубыми. Они оправдываются тем, что члоны ~ играют относительно ма­лую роль по срашевшо с с»Т и q.

Сохраняются н все остальные свойства разобранного выше случая колебаний плоского фронта пламени. Очевидно, в последнем случае Т71Эфф = Uv

DV.

(16.10)

2 1 Г2(к~

Дадим для двух последних случаев систему уравне­ний, аналогичную системе (15.7). Это можно сделать, подставив найденные значения Jх, /2 и /3 (16.8) в урав­нения (15.7). Однако поступим несколько иначе. Если воспользоваться значениями /3 и /3, записанными в виде формул (16.2), (16.3) и (16.4), учесть определение (16.5) и кинематическое условие (16.6), то, пользуясь равенствами (15.8), нетрудно определить значення велнчш

1 о f V* . ,г.

Подставив пх непосредственно в систему уравнений (15.2), получим условие па 2 в следующем виде:

QyU^— ^ ( — ) — QsU, (q.2 — g,) =

T — of f Vl

При записп этой системы эффективная скорость рас­пространения пламепи f/эфф по отмечается каким-либо особым индексом. Наннсанная система получена из общих уравнений (15.2). Нетрудно видеть, что она совпадает с обычнымп условиями, накладываемыми в газовой дина­мике па плоские поверхности сильных разрывов, п отли­чается от них только слагаемым, соответствующим теп­ловыделению.

Дополним эту систему кинематическим условием

V^U^v^U,. ‘ (16-11)

Показывающим, что левая и правая стороны фронта пла­мени движутся относительно наблюдателя с одинаковой скоростью.

Проведеш линеаризацию уравнении (15.10) п (lti. ll), переходя одновременно к безразмерным переменным. При этом учтем, что в установившемся течении Vj_ + U J = = C2+Z72=: 0 и предположим, что вследствие однород­ности смеси и постоянства полноты горения величина q1 — q2 постоянна. После ряда опускаемых здесь простых преобразований получим следующую систему уравнений, описывающих свойства плоскости разрыва 2 через без­размерную вариацию скорости распространения нламени относительно холодной смеси:

1

М,

(16.12)

Х(ЗС — 1) Л?2

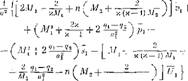
Нетрудно видеть, что если полошить Ь— — ■ г.1,, т. е. как бы остановить фронт пламени, то подученная система совпадает, как и следовало ожидать, с системой (15.7) нрц условии, что в последней Р*, Q* J j, /2, J3 п ї|0Г + </д приравнены нулю. Входящие в систему (КІ.12) величины

2 tj о)

——и л могут быть определены по формулам (15.9) и (15.10).

Система (10.12) удобна в тех случаях, когда в зопе горе­ния задамтт колеблющийся теплоподвод, а пространствен­ные колен, шил фронта пламени. Обычно последпне зада­ются через колебание некоторой аффективной скорости распространения пламени.

Напомним еще раз, что прп пользовании системой (16.12) следует иметь в виду, что положительное значение (Jх соответствует уменьшению абсолютного значения ско­рости распространения пламенп по частицам газа (газ те­чет слева направо, а иламя бежит против течения). С уче­том принятого правила знаков интенсификации процесса горения будут отвечать отрицательные Uv

Идеализированная схема вибрационного горения. 13 на­чале настоящего параграфа было показано, что вместо сложного процесса горения внутри зоны ст в расчетную схему можно ввести векоторую плоскость теплоподвода 2 с тем, однако, условием, чтобы она содержала некоторые источники массы, импульса и эпергии. Хотя такое пред­ставление процесса вибрационного горения не может вызвать возражений по существу, ему недостает нагляд­ности.

Рассмотрим вопрос о том, как можно рациональным образом заменить действительный процесс горепня внутри ст другим, простым и наглядным процессом, причем так, чтобы не потерять прп переходе к этому новому процессу никаких существенных для возбуждения акустических колебаний свойств реального процесса горения. Приведен­ные несколько выше при. меры позволяют предложить в ка­честве эффективного идеализированного процесса возму­щенного горепия процесс, складывающийся из двух основ­ных: возмущения теплоподвода и возмущения положення плоского фронта пламени. Выше уже говорилось, что этн процессы нельзя свести друг к другу II поэтому пз трех независимых велпчпп, которые нужны для связи (без на­рушения трех уравненпй сохранения) произвольно задан­ных слепа и справа от ст возмущений р, v и s, две уже име­ются. В качестве третьей величины можно взять, например, вариацию Р*, которую удобнее всего представить себе как варпацпю гидравлического сопротивления камеры сгорания прн колебаниях параметров набегающего па нее холодного течения.

Первое уравнение системы (15.7) содержит в качестве параметра, характеризующего возмущение процесса горе­ния, Jv второе содержит Мг (Jz — f Р%) и третье содержит

(16.13)

Горения.

Если заменить некоторый реальный процесс, опреде­ляемый этими величинами, простым эквивалентным про­цессом предложенного здесь типа, то необходимо потре­бовать, чтобы соответствующие слагаемые во всех трех уравнениях (15.7) были равны таким же слагаемым в аналогичных уравнениях эквивалентного процесса. Это приведет к следующим трем равенствам (записанным с учетом формул (16.8)]:

Іг^Л^ + и le), Qi йсг + ?і) + 2м; (/, + §’*) =

Величины U 1э и Р*э являются эквивалентными возмущениями теплоподвода, скорости перемещения пло­ского фронта пламени относите1 льно частиц газа и гид­

Равлического сопротивления зоны определить из равепств (16.13)

C/’iD = —r — Vi А

(16.14)

РІ„ = РІ+12,

Qі, Л і -2ійі(Ч сг + 70-^Л-

Таким образом, каким бы сложным ни был реальный процесс внутри о*, его всегда можно заменить некоторым эквивалентным, который слагается из эффективного воз­мущения теплоподвода () ‘,. возмущения скорости раенро- страпепия некоторого эффективного плоского фропта пла­мени U1Э и эффективного возмущения гидравлического со­противления камеры сгорания Р%. Такая замена возмож — иа по только тогда, когда известны все топкости идущих внутри а процессов, позволяющие вычислить JL, J,, Чет и т. д. Достаточно_знать (из эксперимента или ка — клм-либо иным образом) р, v и їпо обе стороны а, чтобы сразу найти эквивалентный процесс в зоне горения. Действительно, воспользовавшись равенствами (16.13),
можно исключить из уравнений (15.7) все величины, описы­вающие фактический ход сложного процесса горения внут­ри а и заменить их соответствующими величинами экви­валентного простого процесса. Тогда зпапио vu sv р<2, v, и s2 сразу позволяет найти из преобразованных урав­нений (15,7) 11ъ, Рхэ и Q*• Очень часто, особенно в теоре­тических исследованиях, пренебрегают суммой Р% + J% во нтором уравнении системы (15.7). Тогда, очевидно, Р*э = 0 и процесс нестационарного горения полностью характеризуется эффективными значениями возмущения теплоподвода н скорости распространения плоского фрон­та пламени.

Обнаруженная здесь возможность введепия в расчетную схему вместо сложного процесса в зопе горения ст простого эквивалентного процесса позволяет в дальнейшем изло­жении говорить лишь о возмущеппи теплоподвода и воз­мущении скорости распространения пламени. Читателю будет нетрудно разобраться самому, когда в этих случаях идет речь об «эффективных», а не о реальных величинах. Для упрощения записи ниже индексы «э» у Q*, i/j п Р* будут всюду опускаться.

f h-L

Система уравнений (15.7) в случае описання процесса вибрационного горения при помощи величин Q*, Сгх и Рхх приобретает следующий вид:

1

-щ Щ 4- Рз

1

2

(х—1)Д/2

= Жзл/’ + СТА+к Ь + 2л/’-40»< ^

+ 2М(Л3иі + Ц*)і .

Здесь величины и А3 вычисляются по формулам (1В.9). Еслп в зону горения поступает воздух, а не подго­товленная горючая смесь (т. с. если смесь готовится внут­ри зоны ст, сводимой далее к плоскости 2), то величина Qt обращается в нуль, поскольку в этом случае = 0.

В заключение надо пояснить одно свойство, которым должно обладать эффективное гидравлическое сопротивле­ние Р*. Поскольку оно вводится для того, чтобы связать без нарушения закона сохранения пмпульса задаваемые, вообще говоря, произвольно возмущения параметров те­чения слева и справа от ст, то фаза Р* может не совпасть с фазой возмущения скоростного напора течения неред зоной а. Это не должно смущать читателя, так как и фак­тическое гидравлическое сопротивление реальной камеры сгорания при нестационарном характере процесса горепня вовсе по следует за изменением скоростного напора набе­гающего потока. Сложный характер течения в области пптенспвного егорання, связанный с периодическим ннхреобразовапием и с тем, что расположенные в зопе горения устройства (стабилизаторы и т. п.) то целиком, то частично обтекаются холодными и горячими стру­ями газа, нарушают привычную для стационарных тече­ний картину следования сопротивления за скоростным напором набегающего потока.

§ 17, Приведение условий на плоскости разрыва 2 к каноническому виду

Полученная выше система уравнений (15.7) [или (16.15)] может быть непосредственно использовапа для связи возмущенных параметров течения но разпые стороны плоскости сильного разрыва Особый интерес представ­ляет нрн этом такое написание этих связей, при котором оказалось бы удобным анализировать влияние процесса горения па возбуждение колебаний. Говоря точнее, жела­тельно придать системе (15.7) такую форму, которая, с од­ной стороны, была бы достаточно простой, с другой сторо­ны, наиболее полно передавала бы физическую сторону изучаемых процессов. Дело в том, что сами величи­ны J j, /2, /8 и Q [так же как и Q*t U~x п Р* в уравне­ниях (16.15)] не являются нор впчпьтми, и поэтому

V наиболее рациональное написание системы (15.7) или (16.15) пока не очевидно.

Существенную помощь в этом вопросе может оказать энергетическая точка зрения па процесс возбуждения акустических колебаний теилоподводом, которая разви­валась в предыдущей главе. Было иоказаио, что элемен­тарные процессы возбуждения колебательной системы за счет одного из двух источников энергии связаны с отли­чием от нуля разностей —и —Поэтому оказалось целесообразным записать связь между возму­щениями параметров течения слева и справа от области теплоподвода при помощи системы равенств (11.11).

Будем называть запись (11.11) канонической и поставим своей целыо приведение соотношений для плоскости раз­рыва 2 к каноническому виду. Предварительно приведем. условия (11.11) к безразмерной форме

Nv2 — — бЕ, трг — рх — ЬХ, gs2 — sx — бS. (17.1)

N fl" >C>Po ‘V2 r>

Одесь = —m — —, g" = —Ј— . J3 тех случаях, когда аі ср і аюжпо не учитывать изменения теплоемкости газа прп его

Нагревании, g = 1, а т = Jp.

Система (15.7) приводится к каноническому віщу путем несложных алгебраических преобразовании. Положив придадим левым частям равенств тог же вид, кото­рый имеют левые части (17.1); в правых частях получим линейные функции переменных, входящих в систему (15.7). В результате будем иметь:

Трг аЛ]рг + а%грх + a23sx + b21 JL + b2Jг -{-

Gsz — = a3lvx + aHpx + a33sx — I b-MJx + bmJ8 +

Значения коэффициентов aik и bih удобнее всего нахо­дить чпслепно, в процессе приведения системы (15.7) к виду (17.2). Сравнивая равенства (17.1) и (17.2), легко найти выражения для ЬЕ, ЬХ п bS. ІІри этом сразу бросается в глаза, что величины ЬЕ, ЬХ и bS составля­ются из двух групи слагаемых: одной, зависящей от воз­мущений параметров течения vv рх и перед плоскостью 2 (перед зоной горения), п другой, зависящей от возмуще­ний самого процесса горенпя (Jv /2, /3, Q).

Поэтому естественно написать:

ЬХ = 6Х0 + ЬХ’, (17.3)

BS = bS0—bS’, )

Где

ЬЕ0 = апиг + апр1 +

ЬЕ’ = + BnJ2 + bl3 (2Щ Js + Q), = Q),

B, s, = a3lvL -f a32 px + aagSj,

65′ — &3aA 4- b32J2 + 633 (2M 73 4- Q).

Величины. ЬЕ’, ЬХ’ и 65′ характеризуют нестационар­ные процессы, идущие в зоне горения, и в этом смысле могут полностью заменить величины Jv /2, 2MJ$—Q. Что касается слагаемых ЬЕ^, 6.Х0 п bS0, то их можно рассматривать в качестве координат начала отсчета вели­чин ЬЕ’, ЬХ’ и 66".

При таком способе написания условий на поверхности 2 может возникнуть недоумение следующего рода. В кано­нической записи (17.1) правые части (величины ЬЕ, ЬХ и 6l>) зависят не только от процессов, идущих в зоне горе­ния (6/Г ЬХ’

U 65′), но и от характера колебаппй в бли — жайшей окрестности зопы горения (6Я0, 6Х0 п 650). В то же время в предыдущей главе было показано, что вели­чины ЬЕ, ЬХ и bS определяют устойчивость процесса.

Получается, что возбуждение акустических колебаний ( связано пе только с процессами внутри зоны теплоподвода.

Дело в том, что одни и те же процессы в зоне горения действительно дадут различпый эффект, будучи поставле­ны в различные условия в смысле характера колебаний окружающей среды. Например, как уже было показано ранее, периодическое тепловыделение в неподвижном га­зе даст тем большие колебания, чем бдиже плоскость под­вода тецла расположена к пучпостп давления; будучи по­мещена в сечение, в котором расположен узел давления, Поверхность теплоподвода вообще не возбудит системы (для Простоты здесь ие оговариваются фазовые условия возбуж­дения) .

Следовательно, в принятой здесь форме заппен учтены оба фактора — как процессы в зоне теплоподвода, так и характер колебаний в ее окрестности.

Следует, конечно, различать, что именно и в какой мере способствует развитию колебаний в каждом данном кон­кретном случае — процессы в зоне горения или особен­ность положения этой зоны относительно стоячих волн, возникших в системе.

Запись условий на 2 в виде канонических соотношений (11.11) или (17.1) привлекает своей простотой. Преиму­ществом ее является также то обстоятельство, что она не­посредственно связана с энергетической сутью происходя­щих при возбуждении акустических колебаний процессов. Однако эта форма записи ие является, конечно, единствен­но разумной. Безусловно, могут встречаться случаи, когда возмущения параметров за зоной теплоподвода — v. z, р. г и sz— оказывается желательным выразить непосред­ственно через t’1? pi и Si и характеристики зоиы горения. Система такого рода легко получается из равенств (17.2). Использовав обозначения (17.4), ей можно придать сле­дующий вид:

^ = т К1 + ап) vi + аізРі + ад + Й = ^ [^Я + U + + + 6-Х’], } (17.5)

— 1 — — I

= — Кл + «32Рх + (1 + Яза) S; — г bS’]. j

§ 18. Источники энергии автоколебаний при произвольно с лож пом процессе в зоие теплоподвода

В § 11 было показано, что при одномерном характере течения внутри зоны теплоподвода существует два источ­ника энергии, за счет которых поддерживаются акустиче­ские колебания — внешний тегтлоподвод и поток внутрен­ней эпергии (тепловые члены), с одной стороны, и поток кинетической эпергии, с другой.

Поскольку в реальной зоне горепия процесс ие одноме­рен, остается неясным, насколько этот вывод справедлив п для более общего случая произвольно сложного процесса в зоне теплоподвода. Поэтому прежде, чем ндтп дальше, надо уточнить, насколько правомерным было приведение условий па 2 к виду (17.1) прп произвольном процессе в зоне теплоподвода.

В рассматриваемом общем случае любой процесс в зопе горепия может быть сведеп, как это было показано выше, к процессу подвода к потоку в плоскости 2 энергии, им­пульса и массы. Чтобы пметь возможность как бы взгля­нуть на процессы, идущие «внутри» 2, будем в настоящем параграфе рассматривать но плоскость 2, а сколь угодно малую (по конечную) область о, вдоль которой будут рас­положены источники массы импульса и энергии. Течение внутри а будем считать одномерным, а вследствие малости а считаем нрнмеппмон гипотезу стационарности. Этот прием позволяет приблизить рассмотрение течения, пересекаю­щего плоскость 2 к уже приведенному в § 11 анализу. Существенным отличием рассматриваемого случая от изу­ченного выше будет наличие источников массы и импульса внутри а.

Напишем, как н раньше, закон сохранения энергии для элемента лотока в спстеме отсчета, движущейся вместе с ним, и отдельно для центра тяжести этого элемента.

В спстеме отсчета, движущейся вместе с элементом жидкости внутри области а, можно написать следующее очевидное равенство:

D<&cvT + pclV = dQ* + (18.1)

Здесь —масса элемента, V — ого объем, Q* — количество подведенного тепла, Э’— энергия, вносимая источником массы.

В отличие от обычных термодинамических зависимо­стей в равенстве (18.1) под знак дифференциала взята масса элемента (ибо она переменна) и учтена энергия, подводимая пе только за счет источника тепла, но и вно­симая источником массы.

Величины, стоящие иод знаком дифференциала в левой части равепства (18.1), могут быть найдепы следующим образом.

Пусть элемент жидкости переходит за малое время Дt из положения А А в положение В В (рис. 25). Тогда изме­нение внутренней энергии эле­мента d&%cvT может быть выра­жено формулой

D<?/ff-crT = F&t {Qvdc. TJrcJdqv).

(18.2)

Изменение объем; равно

(18.3)

DV = FAt dv.

Подставив эти выражепия в равенство (18.1), сразу получим следующее соотношение:

Dqvc, T —pdv = dQ + da’,

Где Q и ь’ — интенсивности источников тепловой энергии и энергии, вносимой массой

Da’ —

F At

Физігчсскпй смысл этих Двух величин — количество энергии, вносимой па единицу площади сечения в единицу времени.

Рассмотрим теперь перемещение центра тяжести выде­ленного элемента жидкости. На основания уравнения импульса напишем

Do&v= — FAtdp + dM, (18.4)

Г,

К

Л в л в

Будет

Рис. 25. Смещение элемента течения внутри зоны о.

Где И — п. чпульс, подведенный к элементу жидкости соот­ветствующим источником (в том числе и источником массы).

Воспользовавшись темп же приемами, что п при выводе уранпепня (18.3), можно написать:

Qi> dv -1- v d§v = — dp d ‘U.

Где

Умножая левую н правую части этого равенства на о, после некоторых простых преобразовании находим:

Стоящие в правой части члены имеют следующий смысл: первый член дает суммарпую интенсивность источ­ника энергии, связанного с непосредственным подводом импульса п подводом импульса массой, а второй указы­вает, какая часть этой энергии пошла па сообщение необходимой кппетпческой энергии массе, введенной в рас­сматриваемый элемент жидкости, для того, чтобы введен­ная масса двигалась со скоростью элемепта. Очевидно, что разность этих двух величин дает эффективную интен­сивность источника энергии, связанного с непосредствен­ным подводом импульса. Обозначая эту разность d$", придадим искомому соотношению окончательных! вид:

DQV^-^vdp^do". (18.5) Интегрирование уравнении (18.3) и (18.5) дает {qvcvT)%-(&jc0T)pdv = Q + d’, j

Ґ ґ ^ С < (18-6)

(18.6)

Сравнивая полученные результаты с формулами (11.12) и (11.13), сразу убеждаемся в их близком сходстве. Повторяя дословно все рассуждения, приведенные в § 11, нетрудно убедиться в справедливости вывода о суще­ствовании двух независимых (теплового п механического) источников энергии, поддерживающих акустические коле­бания. Справедливыми оказываются и все последующие

Ю Б. В. Раушенбах

Рассмотрения элементарных процессов в зоне теплопод­вода и т. д.

Т

При получении формул вида (11.17), (11.18) и (11.19) из равенств (18.6) следует помнить, что формально введен­ные источники массы и импульса являются фиктивными. Эти фиктивные источники, как уже указывалось выше, прп установившихся колебаниях в среднем (за цикл) имеют расход, равный нулю, и, естественно, не могут подводить энергии извне. Аналитически это выражается условиями:

Т

О

О