В большинстве случаев различного рода топки, камеры сгорания двигателей и т. п. содержат в качестве одного из основпых алемептов устройства для подготовки горючей смеси. Нередко эти устройства выполняются в виде форсунок для распыла топлива перед зопой горения. Иногда применяются и другие конструкции. Какими бы ни былп устройства для подготовки горючей смеси, если только они существуют, процесс смесеобразования может самым существенным образом сказаться на горении и, в частности, на возбуждении вибрационного горения. Проще всего это видно из таких соображений. Смесеобразование может характеризоваться известной неравномерностью. Еслп эта неравномерность будет к тому же иметь периодический характер, то в зону горения будет попадать смесь с периодически изменяющимся коэффициентом избытка воздуха или с периодически изменяющимся соотношением между горючим в жидкой и паровой фазе и т. п. Это может приводить как к появлению колеблющегося тепловыделения, так и к подвижности фроита пламепп, а следовательно, к поддержанию колебаний. Подобный случай уже рассматривался в § 25. Одпако упомянутый случай не исчерпывает всех возможностей и поэтому приведенные здесь общие соображения целесообразно несколько конкретизировать, оннсав более подробно типичные механизмы поддержания колебаний, связаппыо с процессом смесеобразования.
А) Неравномерная подача горючего. Если по каким — либо причинам горючее подается неравномерно, с известной периодичностью, то в результате возникает горение, которое тоже будет иметь периодический характер. Неравпомерная подача горючего может быть связана с неравномерной работой помп пли иных устройств, подающих горючее. Обычво такая неравномерность не бывает связапа с акустическими колебаниями газов внутри топкп или двигателя. Поэтому, если в результате и возникают колебания процесса горения, то их надо рассматривать как вынужденные колебания. В отличие от автоколебапцй, частота которых определяется свой — гтвами колебательной системы, частота вынуждеиных колебапий определяется внешним воздействием, например числом оборотов помны, подающей горючее, и т. д. Это обстоятельство позволяет легко отличать вынужденные колебания от автоколебаний и, если это необходимо, принимать меры к нх подавлению. Очевидно, что борьба с вынужденными колебаниями такого типа должна вестись путем воздействия па внешние устройства, подающие горючее (измепение конструкции топливного насоса и т. п.). Здесь этот довольно простой вопрос более подробно рассматриваться не будет, так как оп пе относится к основпому содержанию кпиги, носвящениой автоколебательным явлениям.
Если ограничиться только теми случаями, когда переменный расход горючего непосредственно связан с акустическими колебапиями в газовом потоке, движущемся по двигателю или тоике, то одним из основных факторов, вызывающих такое взаимодействие, является влпянпе колебаний давления окружающей среды на расход той липа через форсунки.
Обозначим расход массы горючего на единицу площади сечения трубы, но которой течет воздух, через тг. Как известно, расход — жидкости через форсунку пропорционален корню квадратному пз перепада давлении на форсунке (разности давления нодачп и давленпя в среде, в которой установлена форсунка)
Тг = кх У рг — р, где кх — некоторый численный Коэффициент, зависящий от размеров форсунки и т. н. факторов, рг — давление жидкости на входе в форсунку, р — давление воздуха в трубе.
Поскольку при акустических колебаниях в трубе величина р будет иметь периодическую составляющую, расход горючего тг тоже должен колебаться. Найдем коле — оателыгущ составляющую расхода горючего:
6 Mr = —~кх Ьр. (35.1)
2V Рг— Р
СоставтПрИВЄДЄШШЙ Ф°11МУЛЫ впДио, ™ колебательная вляющая расхода горючего будет сдвинута относи — тольно колебательной составляющей давления окружающей среды на я.
Получепная формула описывает возмущение расхода горючего в сечении трубы, в котором установлены фор — супки, причем величина 6р тоже относится к этому сечению. Однако нередко плоскость расположения коллектора с форсунками и плоскость интенсивного теплоподвода (зона горения) разделены расстоянием, которым нельзя пренебрегать. Тогда связь между акустическими колебаниями и колебаниями количества горючего, которое попадает в зону горения, можно найти из следующих соображений (рис. 67). Пусть плоскость теплоподвода 2 расположена в сечении s = 0, а плоскости расположения форсунок Ф отвечает координата £ = £ф. Пусть, далее, колебания характеризуются частотой со и амплитудами возмущений скорости и давления слева на плоскости 2 Si>0 и bpQ. Входящее в формулу (35.1) возмущение 6р = 6рф легко представить па основании равенств (4.8) и (4.13) в виде
Б/їф = [ ^гфг bV(>+фа ^ б/,° ] е’іШ’
Колебания давлепия Ьрф вызывают колебания расхода горючеі’о В сечении а процесс горения происходит при | = 0. Следовательно, надо учесть еще время пере — поса горючего потоком па расстояние §ф. Очевидно, это время после приведения его к безразмерному виду будет равпо
(Тф > 0, так как |ф < 0). Следовательно, до плоскости 2 возмущение количества горючего в потоке будет доходить с запаздыванием, равным Тф. Если предположить, что, пересекая плоскость 2, горючее сгорает мгновенно, с постоянной полнотой сгорания, т. е.*)
Q* к26тт,
Х) Нпже Q* является сокращенной записью эффективного возмущения теплоподвода Q* (10.14).
ТО
Q‘ = -— Г Vі Ф, (»; °>)Н +
2)’ /),— р L "і
+ ФІ(іф; с v Ml (35.2)
Где к = Kxkv
Полученная формула позволяет сделать следующие замечапия. Прежде всего видно, что в колебательной
Ф ‘Г
Рпс. (57. Положение сечений, ввода горючего (Ф) и сгорания (2) по длине трубы.
Системе действует обратная связь — акустические колебания в зоне горения 2 с амплитудами 6d0 и 6р0 вызывают возмущепне тепловыделения в этой же зоно, равное Q*. Как известно из предыдущего, если при этом выполняются необходимые амплнтудію-фазовые соотношения между Q*, с одной стороны, н 6рп, 6v0>—с другой, то система может возбудиться. Формула (35.2) была получена в предположении, что эти амплптудно-фазовые соотношения реализованы, система находится на границе устойчивости п поэтому (3 = гш. По своему характеру полученная обрат- пая связь соответствует третьему виду обратной связи, рассмотренному в предыдущем параграфе-, — обратной связи с запаздыванием.
Для того чтобы выявить некоторые свойства изучаемого механизма возбуждепия, полезно мысленно разомкнуть автоколебательную систему и рассмотреть ее с несколько нообычпои точки зрения. Пусть существуют установившиеся акустические колебания. Проследим за тем, какие значения принимает Q*; при этом пе будем пока требовать, чтобы полученные значения 77* были (по фазе П. В. Раушепоах и амплитуде) именно такими, какие способны поддерживать акустические колебапия, существование которых предположено. Если обратиться к рис. 06, то это соответствует размыкапшо изображенных схем в точке А, подаче на вход колебательной системы в третьей схеме периодически мепяющегося Q* (например, от некоторого внешнего источника), которое поддерживает рассматриваемый режим установившихся колебаний, и анализу вопроса о том, какое Q* будет получаться в результате действия механизма обратпой связи на выходе из звена 3. Если эти ()* совпадут, зпачнт, замкнутая система будет совершать колебания рассмотренного типа, если они будут различными, то система не будет совершать установившихся колебаний; колебания будут либо демпфироваться, либо происходить с возрастающей амплитудой.
Рассматривая с этой точки зренпя формулу (35.2), зададим со, 6г;0 и 6р0, т. е. весь процесс акустических колебании, и проанализируем в разомкнутой системе влияние §Ф на Q*. Влняиие §ф на выражение, стоящее в прямых скобках, обычно несущественно. Прп изменении |ф в разум — пых пределах это выражение несколько изменяется по абсолютной величине и практически не изменяет своей фазы. Об этом уже говорилось в § 6 при рассмотрении эпюр стоячих волн колебаний. Другое дело миожитель
Ехр ш ^т -|- ^уг-^) ■ При малых Л7 (а это как раз и является обычным случаем) даже незначительное изменение |ф будет приводить к большому фазовому сдвигу Q* относительно заданных 6р0 и 6и0. Действительно, элементарный расчет показывает, что смещение коллектора с форсунками на 5—10% общей длины трубы (Д£ф=0,05-т-0,1) изменяет фазу Q* на — у и более. Следовательно, малым смещением коллектора по длине трубы можно добиться существенного фазового сдвига Q*. Но тогда открывается, казалось бы, такая возможность борьбы с автоколебаниям п. В случае, если действительно реализована обратная связь описанного здесь типа, достаточно незначительного смещения коллектора с форсупками по длипе трубы, чтобы резко пзмепить фазу Выше (см. гл. V) уже гово — рилось, что при должном фазовом сдвиге между Q* и 6/V возбуждение вообще невозможно, поэтому, подобрав на опыте положение коллектора относительно зоиы горения, можно подавить вибрационпое горение.
К сожалению, дело обстоит не так просто. Свойства акустической системы, возбуждаемой гореиием, сложнее описанных здесь наглядных схем. Они будут подробно рассмотрены в гл. IX.
Влияние колебаний давления в камере сгорания па расход топлива может оказаться сущеетвениым в жидкостных реактивных двигателях, поскольку колебаппя давления могут достигать в пих достаточпо больших величин. При этом задача упрощается в том отношении, что зона теплоподвода непосредственно прилегает к головке камеры сгорания, п, следовательно, можно полагать = 0. Более подробное рассмотрение показывает, однако, что само по себе наличие колебании расхода, вызванных колебаниями давления в камере такого двигателя, недостаточно для самовозбуждения системы. Действительно, при увеличении давления расход горючего будет уменьшаться. Если предположить, что сгорапие происходит мгновенно, то получится, что увеличение теплоподвода будет происходить в момепты понижения давлення и система не возбудится. В этом рассуждении скрыто молчаливое предположение, что система может стать неустойчивой только за счет колебапий теплоподвода. Но в данном случае это не так. Как будет показано в гл. X, главным в этом случае является возмущение газообразования.
Для того чтобы система возбудилась, надо изменить фазу газообразования, которая совпадает с фазой горения, относительно фазы р. Такое изменение возможно, если в системе существует запаздывание процесса воспламенения смеси. Подробнее об этом см. § 37 настоящей главы.
Еще более существенными являются, по-видимому, колеоания расхода горючего в устройствах с малонапор — иымц системами подачи горючего, например’ в пылеуголь — льтх топках. В пих угольная пыль подается током так называемого первичного воздуха через специальное устройство (лопаточную горелку) в зону горения в пред — топке, куда подается и вторичный воздух. Еслп в таком нредтонке возникнет вибрационное горение, то сечение, в котором расположены устройства, подающие угольную пыль, может рассматриваться, в первом приближении, как закрытый конец трубы. Прп колебаниях в нем образуется пучность давлення, н поэтому подаваемая первичным воздухом угольная пыль будет испытывать периодически меняющееся противодавление на выходе. Колебательная составляющая противодавления, которая может реализоваться прп вибрационном горении, имеет тот же порядок, что л избыточное (против предтоика) давление подачн первичного воздуха, т. е. в моменты достижения максимального давления в предтопке нодача пыли может почти полностью прекращаться.
Хотя такой механизм обратной связп должен быть весьма мощным, салі ио себе он не способен возбудить колебательную систему — фазе наибольшей подачи топлива будет соответствовать фаза наименьшего давления в предтопке. Однако реально существующие запаздывания (задержки воспламенения), о которых будет идти речь в § 37, позволяют реализоваться нужным фазовым соотношениям между возмущениями теплоподвода и давления.
В заключение следует еще добавить, что иногда может оказаться необходимым рассмотреть более сложную колебательную систему, чем это делается здесь. Колебания противодавления могут вызвать акустические колебания в подводящих пыль пылепроводах (или в топливных магистралях двп гателеп), п тогда появится необходимость изучения совокупных колебаний среды в основной трубе (предтопок, камера сгорания двигателя) и в подводящих топливо трубопроводах.
Б) Колеблющийся расход воздуха. Вернемся к рассмотрению вопроса о возбуждении вибрационного горения в трубе, по которой течет воздух п в которой расположен коллектор с форсунками, подающими жпдкое горючее. Выше уже говорилось о принципиальной возможности возникновения обратной связи в результате влияния колеблющегося в потоке давлення на расход горючего. Однако реализация этого механизма практически невероятна вследствие слабой зависимости расхода через форсупкн со значительным давлением подачи от акустических колебаппй среды. Возможен, однако, в известном смысли противоположный механизм обратной связи. Предположим, что расход горючего строго постоянен. Тогда иоздух, обтекающий коллектор с форсунками, будет уносить с собою одно и то же количество горючего в единицу времени, вне зависимости от мгновенного значения давления и скорости иотока в сечении, в котором расположены форсунки.
Если количество уносимого горючего и будет постоянным, то коэффициент избытка воздуха может претерпевать существенные колебания, вследствие колебания расхода воздуха в сечении, в котором расположены форсунки. Действительно, коэффициент избытка воздуха
Где L0 —отношение массы воздуха, теоретически необходимой для полного сгорания единицы массы топлива, к последней.
В результате акустических колебаний расход воздуха через единичную площадку поперечного сечения потока (Ш будет также колебаться. Это приведет к возмущению коэффициента а:
6а = + = а ( Q + Ж
(а в правой части равенства соответствует невозмущеп — пому зпачепию коэффициента избытка воздуха).
Анализ возможных значений величин q и v показывает, что первая из них, связанная с возмущением давления, обычно певелика. В открытой трубе с дозвуковым течением давление может колебаться лишь на малые доли атмосферы, поэтому величина Q = (равенство написано для изоэнтропического течения газа) пе может превышать 0,05 — 0,15. В то же время слагаемое может достигать величин порядка единицы. (Это происходит тогда, когда колеоательпая составляющая скорости близка к средней скорости течения. Как будет видно из следующих глав, такой масштаб колебаний следует признать обычным.)
Таким образом, в первом приближении можно написать;
= (35.3)
Показав тем самым, что а колеблется в фазе с v. Повторяя почти дословпо вывод, приведенный в настоящем параграфе при рассмотрении зависимости Ьтг от др, можно написать:
• 6а = [ср, (и; 5ф) 5л — ад Pol • (35.4)
Необходимая связь между колебаниями а и колебаниями теплоподвода Q* или скорости распространения пламени V, легко получается, если учесть (об этом уже говорилось в гл. V), что полнота сгорания (точно так же как и скорость распространения пламени) может существенно зависеть от а. Тогда, ограничиваясь, для определенности, влиянием а на полноту сгорания, паппшем:
Ё* = const (35.5)
Формулы (35.4) и (35.5) в совокупности указывают, что и в этом случае имеет место обратная связь с запаздыванием, существенно зависящим от зд. Необходимо подчеркнуть, что, в отличие от предыдущего случая, рассмотренный механизм обратной связи может играть заметную роль прп возбуждении акустических колебаний в трубах, в которых сгорает распыленпое жидкое горючее. Казалось бы, что тогда путем незначительных смещений коллектора можно подобрать такое его положение, нри котором колебания были бы подавленными. Однако н в этом случае по причинам, которые будут изложены ниже, такой метод борьбы с вибрационным горепнем оказывается малоэффективным.
В) Колебания качества распыла. Вследствие того, что при акустических колебаниях появляются периодические составляющие у скорости н давления, происходят периодическое изменение п скоростиого напора потока ди2/2. Как известно, при работе форсунки в потоке воздуха траектории движепия капель распыленного топлива (дальнобойность форсунки), тонкость распыла п пные связанные со смесеобразованием параметры (в частности, испарение) и сильной степени зависят от скоростного иаиора набегающего на форсупку течения. Поэтому качество распыла также мепяется периодически, строго следуя за акустическими колебаниями в потоке. В результате в зону горения поступает смесь горючего с воздухом, которая имеет периодически изменяющееся качество. Это приводит к тому, что в процессе горепия реализуются отлнчпые от нуля колебательные составляющие эффективного возмущенного теплоподвода Q* и эффективной возмущенной скорости распространения иламепи Ux, т. е. смогут поддерживаться автоколебания системы. Особенно заметную роль описанный механизм обратной связи может играть при условии, что перподігчески изменяющееся качество смеси оказывается во взаимодействии с важными конструктивными элементами камеры сгорания. Мыслимы, например, случаи, когда колеблющиеся траектории полета капель горючего то направляются непосредственно на стабилизатор, то попадают в струп воздуха, движущиеся на известном расстоянии от стабилизатора, пли периодически попадают па стенки камеры сгорания. Во всех этих и подобных случаях колебание качества распыла должпо сказываться наиболее сильно, поскольку оно непосредственно влияет па самые ответственные участки камеры сгораппя.
Если такой механизм обратной связи реализован, то может оказаться полезным изменить взаимное положение элементов топливпого коллектора п элементов камеры сгорания. Эти изменения приходится производить чисто эмпирически, так как подробное изучение взаимосвязи нестационарного смесеобразования с нестациопариым горением является еще далеко не решенной проблемой, тре — оующеи очень глубокой теоретической проработки и тонкого эксперимента.
Если поставить более скромную задачу: дать внешнее описание рассматриваемого явлепия с целью получения формул, снизывающих Q* и 0 с pQ и ~vQ, то после введения какоп-лноо правдойодобной гипотезы о связи колебании дальнооопыостп форсунок или качества расиыла с процессом горения можно Получить формулы того же типа, что и иjiiiведенный выше (35.2), (35.4) и (35.5). Здесь, так же как и в предыдущих случаях при получится обрат
Ная связь с запаздыванием.
Если просуммировать сказанпое в настоящем параграфе, то следует прежде всего указать па то, что даже небольшое число приведенных примеров дает возможность утверждать, что процесс смесеобразования может явиться основой для возникновения целого ряда механизмов обратной связи. Совершенно ясно, что описанные выше отдельные механизмы — связанные с меняющейся подачей горючего, с изменением коэффициента избытка воздуха, с качеством распыла горючего — чаще всего должны выступать в единстве, как различные стороны одного и того же процесса возмущенного смесеобразования. Конечно, это не значит, что какая-лпбо сторона рассмотренного процесса пе может играть в каком-то конкретном случае ведущей роли; это именно и оправдывает описание различных сторон единого процесса возмущенного смесеобразования в качестве независимых механизмов обратной связи. Общим свойством всех этих механизмов является наличие запаздывания, связанного со временем, которое необходимо потоку, чтобы допести распыленное горючее до зоны горения. Это запаздывание становится равпым нулю только в том случае, если горючее подается непосредственно в зону горения.
§ 36. Механизмы обратной связи, имеющие в основе гидромеханические явления
Если бы смесеобразование было единственным процессом, способным обеспечить реализацию некоторого механизма обратной связп, то с вибрационным горепием было бы чрезвычайно просто бороться. Достаточно было бы готовить горючую смесь в отдельном ресивере, акустически изолированном от камеры сгорапня, чтобы вибрационное горепне никогда не возникало. Однако прямые опыты опровергают это. Были, например, поставлены эксперименты по возбуждению вибрационного горения в трубе, которая обдувалась не воздухом, а заранее подготовленной смесыо бепзииа с воздухом. Эта смесь готовилась в отдельном ресивере, опытная установка была выполнена по схеме, близкой к той, которая приведена на рис. 60. Разрыв между трубой, п которой располагалась зона горения, и соплом, подающим б ензо-воз душную смесь, превышал калибр трубы. К тому же подающая смесь труба имела больший диаметр, чем труба, в которой располагалась камера сгоранпя. Все это приводило к тому, что колебания, происходящие в трубе с камерой сгоранпя, никак не передавались в ресивер, в котором были расположены форсунки и готовилась смесь. Это обстоятельство было подтверждено прямыми заме рамп колебаний давления в ресивере. Таким образом, полностью исключалось возможное взаимодействие акустических колебаний в трубе со смесеобразованием, идущим в ресивере. И все же вибрационное горение возникло. Приведенные на рис. 51 результаты опытов были иолученьт па такой именно установке.
Отсюда следует, что помимо смесеобразования могут существовать какие-то другие процессы, которые дают возможность образоваться обратной связи. Ряд этих процессов можно объединить по тому прпзпаку, что все они связаны с гидродинамическими процессами в движущемся ио трубе газе. В основе этой группы механизмов обратпой связи лежит то, что возникающие при горении акустические колебания существенно изменяют характер течения, сообщая ему периодическую составляющую. Чтобы придать этому общему утверждению известную наглядность, приведем здесь результаты одного эксперимента.
В лабораторной установке, на которой изучались некоторые вопросы вибрационного горення, использовался термоанемометр, позволяющий записывать мгновенные значення скорости потока. Этот термоанемометр был установлен перод зоной горения. Прп установившемся вибрационной! горении (даже малой интенсивности) амплитуда и период колебаний скорости потока становились строго иостонппымп, причем наблюдавшиеся до этого турбулентные пульсации скорости как бы «исчезали» на фоне четких колебаний, имевших акустическую природу. Дне осциллограммы — одна соответствующая нормальному горению, другая вибрационному — приведены на рис. Ьб. Следует добавить, что при перемещении термоанемометра по диаметру трубы амплитуда колебании
скорости hp изменялась сколько-нибудь заметным образом, т. е. поток воздуха колебался как целое. Такие упорядоченные колебапия больших масс газа способны, конечно, существенным образом повлиять на характер течения, в частности па впхреобразованне в потоке.
А) Вихреобразоваипе перед зоной горения. В участках двигателя или топки, предшествующих зоне горения, практически всегда присутствуют элементы, дающие возможность возникнуть заметному вихреобразовашпо. Таким элементом может явиться крутой поворот оси течения, расширяющийся участок трубопровода, достаточно резкое изменение площади трубопровода, накопец, просто присутствие плохо обтекаемого элемента конструкция внутри трубы. Прп нормальном режиме работы камеры сгорапия вихреобразовапие во всех этих случаях будет происходить но обычным законам гидромеханики. Если же возникает вибрационное горение, то па основпое движение потока окажется наложенным упорядоченное колебательное изменение скорости течения н тогда впхреобразованне будет происходить пе при обычном обтекании твердых тел потоком, а при обтекании их потоком, скорость которого имеет заметную и упорядоченную периодическую составляющую.

У
Гис. G8. Осциллограммы колебаний скорости перед зоной сгорания: вверху нормальное горение, внизу— режим виСращюн — аого горепия.
Впхреобразованне связано с вязкостью жидкости, а теория течения вязкой жидкости составляет один из очень сложных и еще далеко пе разработанных отделов гидромеханики. Тем более это относится к вопросу об обтекании твердых тел потоком, скорость которого имеет периодическую составляющую. Хотя теория этого процесса, по существу, отсутствует, известны работы экспериментального характера, посвященные близким вопросам, в частности вопросам обтеканпя вязкой жидкостью колеблющихся твердых тол (например, работы, посвященные гэанмо действию вихреобразовання за фабричными труба-
мті прп ветре с собственными колебаниями этих труб). В этих работах показано, что при колебаниях твердого тела с определенной частотой частота срывов вихрей может перестроиться и стать равной этой «задающей» частоте. Важно при этом отметить, что и само впхреобра — зованпе становится в этом случае более мощным.
Естественно поэтому предположить, что если возникло вибрационное горение, то в результате колебаний воздушного потока около неподвижных твердых тел вихреобра — зование перед зоной горения может перестроиться и начать происходить с частотой акустических колебании.
Этому могут способствовать и колебания давлепия. Приведенные во второй главе эпюры стоячих волн давления показывают, что в участках, отдаленных от пучности давления, существует отличный от нуля градиент давления, взятый вдоль оси течения. Из теории течения вязкой жидкости известно, что наличие в потоке градиента статического давления определенного знака может приводить к отрыву потока от стенок вследствие влияния этого градиента па течепие жидкости в пограничном слое. Не вдаваясь в подробности, связанные с этим вопросом, укажем лишь, что во время акустических колебаний градиент статического давления будет периодически меняться, изменяя, в частности, и свой зпак каждые иол — периода. Поэтому, грубо говоря, в течение каждого периода колебаний будет существовать момент, когда отрыв пограничного слоя (т. е. образование вихря) будет особенно вероятен.
Таким образом, не только колебания скорости потока, по и колебания давления будут способствовать вихреобра — зовапшо с периодом, равным периоду акустических колебании.
Можно, наконец, привести пример возбуждения акустических колебаний в аэродинамической трубе, подробно исследованный С. ГІ. Стрелковым, Г. А. Бендрпковым 11 Н. Д. Смирновым1). Не приводя описания этого интересного исследования, укажем лишь, что существенную
Ной* ИТл°Лй0а а П" Бовдрнкоя Г. Л., С м и р — ігмпг/Ьапп»,,.’,’ "ульсации в аэродинамических трубах и способы демпфирования их, Труди ЦАГЙ. Лк 593, Ш6.
Роль в процессе автоколебании играло периодическое образование кольцевого вихри под действием акустических колебании.
Таким образом, ряд косвенных экспериментальных данных и теоретические соображения общего характера указывают на то, что за теми элементами конструкции двигателя или топки, которые допускают заметное впхреобразованне, прп акустических колебаниях в потоке
|
А |
В |
||
|
и. |
—j |
Л
Рис. 6У. Схема вихрс-образовйпия перед зоиой горения.
Могут срываться мощные вихри с периодом, равным периоду акустических колебаппй.
Предположим, что эта возможность реализована, н проследим, каким образом это приводит к замыканию обратной связи при вибрационном горении. На рис. 05), в верхней его части, дано схематическое изображение обсуждаемого явления. В холодной части трубы, в точке А, расположено место срыва потока и образования вихря. На схеме это плохо обтекаемый козырек. На самом деле, как уже указывалось выше, это может быть место поворота течения пли область течения в расширяющемся канале п т. д. Образовавшиеся в точке А вихри сносятся потоком в сторону зоны горения. Пусть период акустических колебаний будет Т. Тогда при скорости течения vx расстояние между вихрями будет LB~v1T. Если считать, что на участке от козырька А до стабилнзатора В скорость течения не меняется, то подходящие к зоне горения ішхри будут периодически С с периодом, равным —всту-
V V у
Иать во взаимодействие с фронтом пламенп, удерживаемым стабилизатором. Это и приведет к замыканию обратной связи. Действительно, пусть существуют акустические колебания, которые приводят к образованию цепочки вихрей, движущихся к зопе горенпя. Подходя к фронту пламенп, каждый вихрь деформирует его, а следовательно, фронт пламени будет испытывать перподпческпе деформации. В гл. IV уже было показано, что периодическое перемещение фронта пламени внутри зоны горенпя эквивалентно существованию отлпчпой от пуля амплитуды колебаний эффективной скорости распространения пламени Uv что само по себе способпо возбудить систему (или поддерживать возникшие автоколебания), если выполняются соответствующие амплитудно-фазовые соотношения. Следовательно, если в точке А образуется достаточно мощный вихрь, который срывается и начинает двигаться вместе с потоком в такой момент времени, чтобы прийти к фронту пламени п деформировать его в долитой фазе акустических колебаний, то колебательная спстема возбудится.
Борьба с вибрационным горением, происходящим по этой схоме, мыслима двумя различными методами. С одной стороны, положительный эффект можно ожидать в том случае, если измепить фазу отрыва вихря, с другой, — если уменьшить его размеры. Что касается первого пути, то надо сразу сказать, что воздействовать на фазу такого сложного явлення, как отрыв впхря, очень трудно. Еслп же поіітп по второму нутп, то простое конструктивное мероприятие — установка спрямляющих решеток на пути следования вихря — может оказать существенное воздействие па процесс вибрацноппого горения. Спрямляющие решетки употребляются, как пзвестно, в тех случаях, когда оказывается необходимым «успокоить» течение, придать всем его струйкам направление, параллельное стенкам трубьт. Эти решетки представляют собою набор тонкпх пластин, обычно пересекающихся иод прямым углом, установленных в каком-либо сечении трубы так, чтобы плоскости пластинок были параллельны оси течения. Обычно оказывается достаточным установитьносле- довательно две такие решетки на некотором расстоянии друг от друга. Решетки эти могут обладать малым гидравлическим сопротивлением и пе менять сколько-пибудь существенным образом характер течения, если не считать его «успокоения». Действие этих решеток сводится к тому, что большой вихрь, пройдя сквозь такую решетку, как бы разрезается на мпого маленьких вихрей. В результате к зоне горения вместо одного мощного вихря, способного сильно деформировать поверхность фропта пламени, подходит совокупность большого числа мелких вихрей, которые воздействуют на пламя по как фактор, деформирующий его поверхность, а просто как ноток несколько повышенной турбулентности. Хотя процесс горения и зависит от турбулентности набегающего потока, эта зависимость ие может идти ни в какое сравнение с мощными искажениями конфигурации фропта пламени большими вихрями. В пижией части рис. 69 дана схема течения при установке перед зоной горения спрямляющих решеток С.
Высказанные здесь общие соображения были подтверждены специальными экспериментами. Схема экспериментальной установки по существу изображена на рис. 69. Труба, в которой была расположена камера сгорания, обдувалась свободным потоком. Входная часть этой трубы допускала возникновение мощных вихрей. Для того чтобы разорвать возникающую при этом связь между процессами вихреобразовапия и горения, в сечениях, близких к зоне горения, были установлены две спрямляющие решетки. Опыты заключались в том, что изучался процесс горения (с точки зрения возможности возбуждеппя вибра — циоплого сгорания) со спрямляющими решетками и без них. При постепенном увеличении подачи горючего (умепыненип коэффициента избытка воздуха а) наблюдалось изменение характера колебаний.
Предварительно было определено влияние спрямляющих решеток на степень завихренности воздушного течения перед зоной сгорания. Это производилось следующим образом. При холодной продувке установки, путем дрос- солпривання выходного сечения трубы, получался тот же расход воздуха через установку, что и расход, который наблюдается ирн горении. Затем в сечении, лежащем за вто])ой спрямляющей решеткой, при помощи термоанемометра определялась степень завихренности течения. Здесь сЛедует оговориться, что термин «завихренность»
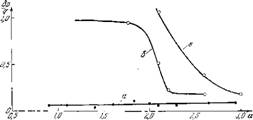
Рис.. 70. Влшшие вихреобразованіга перед зоной горения на склонность системы к возбуждению,
Применяется в настоящей книге для обозначения турбулентности большого масштаба, образовавшейся в результате срыва больших вихрей в участках трубопровода, лежащих перед камерой сгорания.
Результаты измерения колебаний скорости дали степень завихренности без спрямляющих решеток 70%, при установке спрямляющих решеток — 20%. Относительно приведенных здесь численных данных надо заметить следующее. Применявшийся в опытах термоанемометр не был приспособлен для замера столь интенсивной турбу — лентпостп. Поэтому приводимые здесь численные данные сле/;ует рассматривать как качественную характеристику степени завихренности потока. Они не оставляют сомнения в том, что установка решеток заметным образом уменьшает степень завихреппости потока.
Результаты опытов приведены на рис. 70, на котором даны амплитуды колебаний давления перед зоной сгорания ор в зависимости от коэффициента избытка воздуха.
Крпвая а характеризует работу установки при наличии спрямляющих решеток, кривая в — без них. Как/видно пз экспериментально полученных кривых, установка спрямляющих решеток ликвидирует мощпое вибрационное
Горение ^ 1 ^ и сводит колебапия давления к нормальному уровню < ОД При этом осциллограммы зафиксировали различный характер самих колебаний, При вибрационном горении (кривая в) колебания носили совершенно четкий и регулярный характер, при пормаль — пом горении (крпвая л) наблюдался сложпый и неопределенный спектр частот.
Таким образом, в описанном опыте (и ряде других) совершеппо ясно сказалось благотворное нлияпие разрыва связи между вихреобразоваппем перед зопой горепия и процессом сгорания.
Конечно, установка спрямляющих решеток не является единственным способом разрыва этой связи. Если вихреобразование обязано своим возникновением наличию плохо обтекаемого тела во входных участках, то тот же эффект может быть достигнут удалением этого тела или приданием ему удобообтекаемой формы. Важность таких мероприятий иллюстрирует кривая б на рис. 70. Эта кривая соответствует опытпой установке со спрямляющими решетками, отличающейся тем, что за решетками на стенках трубы располагались (из конструктивных соображений) бабышкп в форме параллелепипедов. Когда им была прпдапа удобообтекаемая форма, вибрационное горение прекратилось и относительные амплитуды колебания давлеппя упалп до допустимого уровня ~ ^ 0,1.
Надо сказать, что общих, стандартных средств борьбы с вибрационпым горением, возникшим в связи с вихре — образованисм в холодпоп части течения, не существует. В каждом конкретпом случае па до находить источник этого вихреобразовапия и принимать соответствующие меры. Иногда это будет установка решеток или придание удобообтекаемой формы телам, в другпх случаях это может быть установка направляющих устройств (например, направляющих лопаток па участках крутого поворота течения), отсос пограничного слоя или другие меры, хорошо разработанные экспериментальной аэродинамикой.
При желании представить рассмотренный механизм обратпой связи в виде аналитических зависимостей возникают известные трудности. Они связапы с недостаточной разработкой вопросов впхреобразованпя н отсутствием количественных данных о влиянии приносимого в зону горенпя вихря на изменение конфигурации фронта пламенп.
Если этимп данными задаться (нлп, изучив обсуждаемое явление экспериментально, воспользоваться опытными данными), то дальнейший путь совершенно очевиден. Движение цепочкп вихрей через фронт пламени приведет к периодическому изменению объема горячих газов в зоне горенпя а, и в соответствии с результатами § 16 можно будет написать:
Где, как известпо, V, (0 — объем зоны а, занятый продуктами сгорания, a F — площадь сечения потока.
Расстояние между фронтом пламени и местом образования вихрей Lad (рис. 69) позволит связать фазу отрыва вихря с фазой соприкосновения его с фронтом пламепп аналогично тому, как это делалось в § 35. путем введения
Мпожителя ехр г’и^т’
В результате нетрудно получить формулы того же типа, что н формула (35.2), например:
(36.2)
Последняя формула папдсапа в предположении, что отрыв вихря связан с колебаппямн скорости в точке А, постоянная С включает чпсленпую характеристику отрывающегося вихря (его фазу и амплитуду, которая считается пропорциональной возмущению і? г в точке А). Как видно пз (36.2), и в этом случае возникает обратная связь
С запаздыванием.
20 р. в. Payment*
Б) Вихреобразованис в зоне горения. Другим явлением, которое тоже связапо с гидромеханикой Плохо обтекаемых тел и тоже может стать механизмом обратной связи, является вихреобразовапие за стабилизаторами пламени. Как известно, для непрерывного поджигания горючей смеси, движущейся по трубе, применяются разного рода поджигающие устройства, простейшим типом которых является плохо обтекаемое тело (например, конус, свернутый из лпстового металла п поставленный вершиной навстречу течению), зона обратных токов которого служит непрерывно действующим источником поджигания. Схематически такой стабилизатор показан на рис. 71. Горючая смесь пабегает на стабилизатор А, в аэродинамической «тени» которого существует область А В заторможенного течения; в ней периодически образуются впхрп, сносимые дальше обтекающим стабилизатор потоком. В этой зоне обратных токов скорости невелики, и поэтому процесс сгорания происходит в благоприятных условиях. Ближайшая к зоне обратных токов струя СС находится в течение сравнительно длительного времени в контакте с горячими газами зоны за стабилизатором, она успевает прогреться и пачать гореть. Затем пламя перекидывается в следующую струю DD п т. д.
При нормальном горении процесс впхреобразовання за стабилизатором подчиняется обычпым закономерностям п в общем его характер пе зависит от того, происходит обтеканпе стабилизатора холодный! воздухом или горячей смесью, которая сгорает за ним. При я том фронт пламени за стабилизатором имеет характер несколько подвижного, хаотически деформирующегося конуса, со средним положенном фропта пламени вдоль линий АЕ и AF.
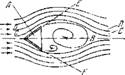
Рис. 71. Схема течения за плохо обтекаемым стабилизатором пламени.
Совершенно другой характер принимает процесс горения за стабилизатором в тех случаях, когда возникает вибрационное сгоранпе. Акустические колебания по тем
Же причинам, которые излагались несколько выше, как бы навязывают свою частоту вихреобразованпю па стабилизатором, причем раз-
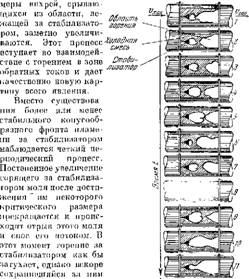
Начальный очаг иламепи дает возможность во — Рис. 72. Ви. хреоПразпваггие за зо б и о виться горению, коническим стабилизатором при горящий объем все бо — впб1>аинонном гореиии (скоростная
Киносъемка).
Лее увеличивается, продолжая «держаться» за
Стабилизатор, с — тем, чтобы по достижении критического размера виовь оторваться от стабилизатора и начать движение вместе с потоком. Совершенно ясно, что этот
периодический срыв горящих молей со стабилизатора является срывом вихрей, в которых (по мере их роста) процесс горения охватывает все болынпе и большие массы горючей смеси.

Описанное здесь явление было зафиксировано скоростной киносъемкой картины горепия за одиночпым коническим стабилизатором через прозрачное окно, вделапное в стенку цплиндрпческой трубы диаметром 200 мм, в которой изучалось вибрационное горение. Последователь-
Пость наиболее характерных
Кадров, запечатленных кп — посъемкой, приведена па рпс. 72. Следует заметить, что в этпх опытах в горючее подмешивались малые количества специального вещества, сообщавшего пламенп
Рис. 73. Осциллограмма на — свойства яркого свечения,
Пней колебаний давления <У, Чтобы показать, что част светимости зоны сгорания Ф стота срыва горящих молен
При вибрационном горении. (частота вихреобразоваппя)
Совпадает с частотой акусти-
Ческих колебаний, в тех же опытах производилась одновременная запись на шлейфовий осциллограф колебаний двух величин — давления н светимости пламени в зоне горенпя. Установленный па должном расстоянии от кварцевого стекла фотодатчик позволял записывать интегральную светимость зоны горения, которая была пропорциональна видимой площади горящих молей. Поэтому периодические отрывы горящих молей от стабилизатора и их постоянное возобновлен пе, показанное па рнс. 72, должпо было привести к периодическому изменению показаний фотодатчпка. Соответствующие записи па ленте осциллографа приведены па рнс. 73. Легко видеть, что частоты колебаний светимости и давления полностью совпадают, что подтверждает факт перестройки процесса вихреобразоваппя и горенпя па акустическую частоту.
Если обратиться к математическому описанию этого типа возмущений процесса горения, то совершенно очевидно, что в зоне а будетпроисходить периодическое изменение объема, занятого горящими газами. Это приведет, как
и в предыдущем случае, к появлению отличной от нули периодической составляющей эффективной скорости распространения плоского фропта пламепи 1/л, величина которой может быть определена формулой (36.1). Если далее предположить, что процесс внхреобразования за стабилизатором связан исключительно с возмущением
— 1 д т — ,л
Скорости течения vv ТО величина -^-р vr (t) может быть (в линейном приближении) представлена как
••„ — I-Kr(0-const5„ •• (36.3)
Где const, вообще говоря, комплексная величина, характеризующая амплитуду и фазу стоящего слева выражения ирп некотором единичном г;,. Таким образом, может быть представлено в виде
(/ = const vr (36.4)
В этом выражении ттостояппый множитель при 0] отличается от постоянного множителя в формуле (36.3), как это в иди о из сравпения выражепий (36.1), (36.3) и (36.4), на единицу.
Если бы оказалось, что срыв вихря связан не только с колебапиямп скорости, но и с колебаниями давлепия, то формулы (36.3) и (36.4) приобрели бы более сложный вид — в правых частях вместо t>, оказалась бы линейная комбинация рх и vv Таким образом, тип обратпой связи характеризуется в этом случае отсутствием запаздывания, порождеппосо переносом возмущающей горение причины потоком, т. е. соответствует схемам, изображенным па рпс. 66, а и б.
В заключение настоящего параграфа сделаем ряд общих замечаний. В приведенных двух примерах обрат — пых связей, обусловленных гидромеханикой течепия, говорилось о влиянии вихреобразовапия на горение и подчеркивалось воздействие вихреобразовапия на величину возмущения скорости распространения пламени Uv Это пе значит, конечпо, что вихреобразоваште не может вызвать нарушений (?*, например, через нарушение смесе — ооразованпя (нрп прохождении вихрем зоны расположения форсунок) или непосредственно, путем изменения полноты сгорания в зоне а вследствие нарушения процесса горения. То же самое можно сказать п о Рх. Периодические срывы впхрей со стабилизатора безусловно приведут к периодическому изменению мгновенного значения коэффициента гидравлических сопротивлений устройств, по — мещеппых в зоне горения. При желапнп можпо было бы учесть п эти две слагающие процесса возмущения горепия, однако здесь, главным образом из соображений экономии места, приведена лшнь наиболее ярко проявляющаяся связь между внхреобразовапием и деформацией фронта пламенп.
В настоящем параграфе всюду говорилось о способности впхреобразования подстраиваться к частоте акустических колебаний. Этот факт наблюдался непосредственно и при изучении впбрацпопного горенпя. Скоростпаи киносъемка картины горения за одиночным коническим стабилизатором, которая приводилась несколько выше, подтвердила существование указанной связи между вихре- образованнем и акустическими колебаниями. Интересно отметить, что «лесепка» частот, приведенная на рпс. 51. была получепа прп горепип заранее подготовленной смеси за коническими стабилизаторами. Зафиксированное скачкообразное изменение частот косвенно свидетельствует о том, что способность вихреобразования подстраиваться к частоте акустпческих колебаний весьма велика.
Надо сказать, что вполне возможно взаимодействие с процессом горения обоих видов вихреобразования — перед зоной горения п за стабилизаторохм. В этом отношении может быть показателей следующий опыт. Гореппе заранее подготовленной горючей смеси производилось в трубе, имевшей камеру сгорания квадратного сечения. В пен изучалась «плоская» задача горенпя. Пламя удерживалось стабилизатором, расположенным посредине потока и выполненным в форме горизонтального углового профиля, поставленного ребром навстречу потоку. В непосредственной близости от стабилизатора, перед ним, ставилась прямоугольная заслонка, перекрывавшая половину квадратного сечения камеры сгорания (заслонка ставилась вплотную к одной из стенок). Несмотря па близость от стабилизатора, заслонка пе попадала в зону юрепия, ее можно было ставить горизонтально и вертикально. В первом случае ее кромка, обтекавшаяся потоком смеси, была параллельна кромкам стабилизатора, во втором — перпендикулярна им. Кроме того, заслонку можпо было поворачивать так, что она становилась «по потоку» и, таким образом, никак пе нарушала характера течения. Опыты сводились к возбуждению в такой спстеме ішбрационного горения с замерами частот и амплитуд колебаний давления. Результаты экспериментов показали, что при вертикальном положении заслонки частоты сохраняли то же значение, что и при заслонке, повернутой «по потоку», однако амплитуды колебаппй при этом уменьшались. Переход к горизонтальному расположению заслонки приводил к уменьшению частоты колебаний вдвое п к увеличению амплитуд колебаний. При объяснении вибрационного горения процессами, связанными с впхре — образованием, этот результат естествен: в первом случае половила стабилизатора как бы затеияласьп таким образом спижалась интенсивность суммарного процесса впхреобразованпн; во втором случае заслонка п стабилизатор могли интерферировать, что приводило как к увеличению интенсивности вихреобразования, так и к изменению частоты срыва вихрей. Последнее привело к возбуждению другой гармоники системы, которая легче согласовывалась с новым характером вихреобразования.
Относительно возможности описання воздействия вихреобразования па процесс горения формулами типа (36.2) и (36.4) надо заметить следующее. В указанных формулах связь между акустическими колебаниями и вихре — образовапием записана в виде линейного соотношения. Между тем интенсивность вихря связана с амплитудами акустических колебаний более сложным образом, так как размеры вихря определяются в значительной степени размерами плохо обтекаемого тела, которое, естественно, не зависит от частоты акустических колебаний. Следовательно, формулы (36.2) и (36.4) могут иметь лишь ограниченное применение. Чтобы описать процесс вибрационного горепия более полно, надо было бы учесть нелинейные соотношения, свойственные процессу вихреобразования.
В принципе это можно сделать, если будут сформулированы соответствующие свойства вихреобразовапия. Пример решепця задачи о вибрацпоппом горении, в котором будут учитываться нелинейные свойства зоны горения, дан в следующей главе.
В заключепне несколько слов о методах борьбы с вибрационным гореннем (еслн опо нежелательно) в случае, когда обратная связь замыкается через впхреобразование. Выше ужо говорилось, что если источник вихреобразовапия расположен перед зопой горения, то установка спрямляющих решеток н другие аналогичные мероприятия могут оказаться полезными. В том случае, когда колебания возбуждаются впхреобріазованием за стабилизатором, дело становится сложнее. Ликвидировать это впхреобразование нельзя, поскольку наличие зоны обратных токов за стабилизатором является обязательным условием его работы в качестве источника поджигания. Кое-что может быть здесь сделано эмпирическим подбором наиболее подходящих геометрических конфигураций стабилизаторов.
В литературе существуют указания на то, что возникающее иногда в промышленных топках вибрационное горение связано ие только с возмущением подачи топлива (речь об этом была в предыдущем параграфе), но и с образованием мощных регулярных вихрей в области подачи топлива в зону горения. В тех случаях, когда вибрациоппое горение является нежелательным, рекомендуется округленно острых кромок и другие мероприятия, облагораживающие аэродинамические обводы соответствующего участка топки. Это практическое правило становится понятным в свете приведенных выше соображении.
Интереспо отметить, что в описаниях процесса впхре- образования в топках, в связи с пульсирующим характером горения в них, подчеркивается, что вихрь, в котором происходит горение, имеет тепдепцшо становиться осо — беппо мощным. Нечто подобное паблюдалось и в описанных выше опытах по впхреобразованию за стабилизаторами при вибрационном горении. Следует, правда, отметить, что вопрос о влиянии процесса горения в вихре іта его свойства еще совершенно не изучен.
§ 37. Механизмы обратной связи, основанные на закономерностях собственно гореипя
Помимо, в некотором смысле, косвенных причин, ведущих к вибрационному горению,— смесеобразования и вихреобразовапия — в самом процессе горения заложепы механизмы, способные сыграть роль обратной связи в этом автоколебательнохМ явлении.
Существование таких механизмов обратной связи, имеющих в основе закономерности самого горения, доказывается, папример, тем, что в уже неоднократно упоминавшихся опытах Коварда, Хартвелла и Джорджсона впбрационное горение возникло в зарапее подготовленной неподвижной газовой смеси, т. е. в условиях, которые полностью исключают какие-либо эффекты, связанные с вихреобразоваинем или смесеобразованием.
Приведем поэтому описание некоторых механизмов обратпой связи, непосредственно связанных с процессом гореппя.
А) Скорость нормального распространения пламени.
‘->та скорость зависит от температуры смеси и ее давления; турбулеитпая скорость распространения может, кроме того, измепяться в зависимости от скорости потока и сте — пепи его турбулнзации. Прп колебаниях газового столба в двигателе все перечисленные параметры потока (за исключением, может быть, степени турбулизации) имеют периодическую составляющую. Следовательно, и ckqt рость распространения иламепи будет меняться периодически. что может1 прсдужнть причиной вибрационного гореипя.
Покажем это па примере возбуждения системы плоским фронтом пламени, скорость распространения которого зависит от температуры смеси и от ее давления перед зоной горения. Поскольку температура ие входит в систему избранных переменпых (р, v, s), то, воспользовавшись уравнением состояния р = $ІІТ и условием адиабатичности s = const, позволяющим связать р и q, представим скорость распространения пламенп как функцию одного лишь давления перед зоной горепия. Обычно зависимости такого рода находятся экспериментально п представляются в виде степенных функции
Где индексами «нуль» помечены начальные значения Ux и pv Рассматривая малые отклонения ил от U{° можно написать
т^и’Гг^. (37.1)
Будем считать, что начальпые значения Ux и pv входящие в формулу (37.1), совпадают с Ux п рх в холодном участке трубы, и учтем, что в силу неподвижности фронта пламенп относительно наблюдателя в установившемся течении vl = — U, переходя к прппятым в книге безразмерным переменным, получим пз (37.1)
И^ -кМіГр. (37.2)
Здесь следует напомнить, что, как уже указывалось в § І6 при обсуждении системы (16.12), увеличению абсолютной скорости распространения пламени, в силу принятого правила знаков, соответствует Ux < 0. Таким образом, при г > 0 увеличению давлепия соответствует увеличение абсолютной велпчнпы скорости сгорания.
Формула (37.2) описывает один из возможных механизмов обратпой связи, непосредственно связаппых с процессом сгорапия. Рассмотренный тпп обратпой связи относится к простейшему, приведенному в верхней части рис. 66.
Основные параметры газового течения, р и v, могут влиять на яозбуждепие автоколебаний не только через Ult но и через Q*. Это будет происходить в тех случаях, когда полпота сгорания окажется функцией, например, скорости течения vv Колебания скорости течения перед зоной горения вызовут тогда колебания полноты сгорапия, а следовательно, и колебания теплоподвода. Если облечь эти рассуждепня в аналитическую форму, то нетрудно получить для Q* выражение, апалогичпое формуле (37.2). Легко сообразить, что для возбуждения акустических колебаний полнота сгорания должна достаточно интенсивно падать с увеличением скорости потока.
Б) Паличне поджигающего источника. Перечисленные иыше мехаиизмы обратной связи могли проявиться и в отсутствие специального поджигающего источника. Наличие такого источника приводит к возможности периодического — нарушения поджигания смесн. Это связано с тем, что практически всегда существует некоторая скорость холодного потока, up и котороіі происходит срыв горения. Скорость эта зависит от мощпостп поджигающего источпика; ее существование обусловлено тем, что для поджигания горючей смеси требуется пзвестцое время контакта этой смеси с пламенем и, кроме того, само пламя должно быть достаточпо мощным, чтобы не быть погашенным потоком. Вопрос этот достаточно подробно излагается в работах по теории горения и поэтому здесь разбираться но будет.
Пусть поджигающий источник, за который «держится» пламя, характеризуется некоторой критической скоростью течения v*t при которой прекращается горение смеси, набегающей на поджигающий источник. Тогда в моменты времеии, когда і^-і-би, > и*, пламя будет отрываться от источппка поджигания п упоснться потоком (конечно, если оно в предшествующие мгновения существовало). В моменты времени, когда v, + 6vi < , процесс поджигання смеси будет возобновляться. Оинсаи- ный здесь механизм обратной связи нередко играет существенную роль. Как правило, этот механизм наблюдается при горении смеси за стабилизатором на режиме сильно развитых колебании. Несколько ниже этот случай будет рассмотрен более подробно. Здесь же целесообразно начать описание подобного механизма с другого случая. Чтобы исключить влияние вихреобразования, были поставлены специальные опыты, в которых заранее подготовленная однородная смесь поджигалась тонкой и плоской газовой горелкой, установлепной в трубе квадратного сечения с кварцевыми стенками. Газовая горелка была выполпеиа так, чтобы пе нарушать заметным образом течения в холодпой части квадратной трубы, а пламя за горелкой (при подаче по трубе чистого воздуха, без горючего) имело форму тонкого, короткого и плоского язычка, протянувшегося посередине квадратного сечения от одной кварцевой стенки каморы сгорания до иротиво — по ложной. При подаче в трубу горючей смеси эта полоска постоянно существующего пламени, питавшегося горючим и кислородом от отдельпого источника, поджигала горючую смесь, двигавшуюся вдоль камеры сгорания. Скоростная кипосъемка через прозрачные стенки каморы сгорапия, которая велась так, что оптическая ось съемочного аппарата была параллельна поджигающему язычку пламенп горелки, т. е. перпендикулярна к нрозрачпой стенке камеры, позволила наблюдать «плоскую» картину горенпя за таким источником поджигания.
В данном случае какие-либо явления, связанные с внх- реобразованием, совершенно исключались. Никаких колебаний непрерывного фронта пламени за горелкой не наблюдалось. Как н при горении за плохо обтекаемым телом, в этом опыте главную роль нгралп срывающиеся с поджигающего псточппка объемы горящего газа, которые росли, перемещаясь вместе с потоком, пока пе заполняли всего сечения. На рис. 74 даны характерные кадры, полученные киносъемкой в этом эксперименте. На приведенных кадрах хорошо видно, как газовая горелка периодически поджигает горючую смесь, в связи с коле — бапиямп скорости смеси. Прп увеличении скорости потока относительно горел кп ее мощность оказывается недостаточной для поджигаиия смеси. Смесь воспламеняется вновь, как только колебательная составляющая скорости течения оказывается направленной против средней скорости течения.
Нечто аналогичное можно наблюдать и при горении заранее подготовленной горючей смеси за стабилизаторами, выполненными в виде плохо обтекаемых тел, при сильно развитых колебапиях, сопровождающихся периодическим «забросом» пламени вверх по потоку, в области, лежащие неред стабилизатором. Более но дробно этот процесс (но с несколько иной точки зрепия) будет рассмотрен в гл. IX.
Аналитическое описание такого явления, как периодический отрыв горящих молей от удерживающего пламя источника поджигаиия, не представляет трудностей. Здесь, как п в § 36, надо рассмотреть периодическое изменение объема горячих газов в камере сгорания V,, (f), перейти затем к эффективному возмущению скорости
Распространения пламени С/, и в конечном итоге получить формулу вида (36.4). Следует, правда, добавить, что такое описание легко осуществить для уже возникших автоколебании. Еслп же попытаться рассматривать этот процесс как механизм возбуждения автоколебании, начиная с бесконечно малых амплитуд, то сразу становится яспым. что подобное возбуждение певозможпо. Ведь отрыв ігппк’іпі от источника поджигания может произойти лишь после того, как амплитуда колебаний скорости достигла необходимой величины. Таким образом, описанный механизм способен проявиться в двух случаях. Во-первых, если начальное возмущение было достаточно большим. Такие случаи известны в теории колебаний как случаи жесткого самовозбуждения. Во-вторых, может оказаться, что первоначально колебательная неустойчивость течепия возникла в результате реализации другого механизма обратной связи, способного сделать систему неустойчивой по отношению к бесконечно малым возмущениям (мягкое самовозбуждение), и лшнь после того, как амплнтуды колебаний заметно выросли, колебательная система изменила механизм обратной связи па опи — саппый выше.
В) Явления запаздьшаиня в зоне горения. Нетрудно построить примеры, когда только запаздываппе процесса сгорапия может дать пужпые для возбуждения акустических колебаний амплитудно-фазовые соотношения между возмущепнямп теплоподвода и возмущениями давления. Покажем это па примере, почерпнутом нз теории воз- буждепия колебапий в жидкостных реактпвпьтх двигателях1).
Как будет более подробно показано в гл. X, при возбуждении продольных акустических колебаний в жидкостных реактивных двигателях наиболее существенным является пе возмущение теплоподвода, а возмущение газообразования (сгорание жидкого топлива разумно рассматривать как процесс газообразования). Этот процесс может быть связан с известным периодом индукции. Аналогичные
Crocco L., Journal of the Ашег. Rocket Society 21, № (і, 103—178, 1951; 22, № 1, 7—16, 1952. Русский перевод: Вопросы ракетной техники, № 3 (9), 1952, стр. 9—31.
S ;>л] механизмы, связанные с {‘прением
Механизмы задержки воспламепення мыслимы и в тех случаях, когда газообразование большой роли не играет, так как количество впрыскиваемого топлива невелико но сравнению с поступающим в область сгорания воздухом, но большую роль играет возмущенпе теплоподвода, связанное с задержками воспламенения (обычные топки).
При рассмотрепии роли запаздывания процессов вос — нламенеппя в процессе возбуждения акустических колебаний в настоящем параграфе будет говориться только о возмущении теплоподвода Q*. Следует, однако, иметь в виду, что все сказанное относятся п к вопросу о возмущении газообразования (и, быть может, в большей степени). Поэтому ниже, в гл. X, основные соотношения, получепные здесь, будут непосредственно прилагаться к вопросу о возмущении газообразования в жидкостных реактивных двигателях.
Предположим, что расход топлива постоянен, а сгорание происходит в момент выхода топлива из сопла мгно — вонио. Тогда теплоподвод не возмущается: — О, и, следовательно, самовозбуждение системы невозможно. Совершенно иной будет картина, если процесс сгорапия топлива связан с задержками во времепп. Прежде чем рассмотреть это, приведем краткие сведения по вопросу о вероятных причинах существования таких задержек.
Ш
Превращение находящихся в жидком состояппн компонентов топлива в газообразные продукты сгорапия требует известного времени; это время естественно назвать периодом индукции. Период штдукцип связан со сложной ценыо физико-химических процессов, происходящих в камере сгоранпя. Этими процессами являются распыл топлива, его подогрев п частичное или полное испарение капелек топлива, развитие химических реакций, которые в конечном итоге приводят к образованию продуктов сгорания. Особенностью многих названных явлении является нх зависимость от давления. При увеличении давления в камере сгоранпя повышается скорость смесеобразования — распыл становится топыпе, испарение н прогрев капелек топлива ускоряется. Кроме того, скорость ряда химических реакций (особепво идущих в газовой фазе) растет с ростом давления. В результате суммарный
пернод индукции может иметь ясно выраженпую тенденцию к уменьшению прп увеличении давления в камере сгорания.
Из сказанного следует, что период индукции можно рассматривать как время, до. истечении которого происходит мгновенное превращение топлива в продукты сгорания. (Последнее связано с тем, что после дол ж пой подготовки смеси она сгорает очень быстро, поскольку скорость реакции чрезвычайно сильно растет с ростом температуры, в частности, подогрев смеси, связанпый с началом ее горепия, делает последующее сгорание практически мгновенным. Копечио, эта картипа является лишь первым приближением к истинным явлениям.)
Определеипе суді мар його периода индукции возможно только экспериментальным путем. Однако, основываясь на сказанном выше, можпо предложить такое соотношение в качестве аналитической зависимости первого приближения:
>и = и — Нш, (37.3)
Где /„o = const, a t(Xі определяется из равенства
/„,// = const. (37.4)
При этом, поскольку увеличению давления должно соответствовать уменьшение периода индукции, ?■ > 0.
По формуле (37.3) период индукции tn состоит из двух слагаемых: первого, txlо, которое не заипент от давления, и второго, taі, связанного с давлением соотношением (37.4).
Ниже будет делаться предположение, что taо—0, п весь период ппдукции может быть связан с давлением соотношением (37.4).
Предположим, что в камере сгорания происходят колебания давления. Тогда вместо соотношения (37.4) естественно ввести аналогичное, но записанное в виде интеграла
T
‘ * 11
Легко видеть, что если р — const, то равенства (37.4) и (37.5) совпадут. Еслп же p~p{t’), то явлеппе становится более сложным. Пусть, как уже говорилось, форсунки подают постоянное количество топлива. При колебаниях давления происходят колебания периода индукция. Уменьшение его приводит к тому, что сгораппе частиц, поступивших в камеру сгорания в определенный момент, совпадает во времени со сгоранием частиц, поданных раньше. Это приводит к уволнченшо тепловыделения против значения, характерного для установившегося процесса. При увеличении периода индукции будет наблюдаться обратная картнпа. Такпм образом, при наличии колебашіи давления вследствие зависимости периода индукции от давления возмущения теплоподвода будут отличны от нуля, что делает возможным само воз буж депие системы. (Для этого необходимо, конечно, пе только Q* ф 0, но и определенное соотношение между фазой возмущения давления и фазой (?*.)
Приведенный пример показывает, что зависимость периода индукции от давления может привести к реализации механизма обратной связи, способного возбудить рассматриваемую колебательную систему.
Выше, в § 35, рассматривался пример, когда колебания давления в камере сгорания вызывают колебания расхода топлива. Там же было указано, что в этом случае возбуждение колебапий возможно лишь тогда, когда в системе существует запаздывание воспламенения смеси, т. е. нужная обратная связь получится только при одновременном действии двух причин, имеющих в оспове смесеобразование и горение соответственно. Легко заметить, что в этом случае для самовозбуждения колебаний пет необходимости предполагать налпчпе зависимости периода индукции от давления, так как отлпчпое от нуля Q* получится за счет переменного расхода топлива. Положив в формуле (37.3) tai = 0, будем иметь /„ = —const. Весь дальнейший ход анализа будет близким к примеру, рассмотренному в § 26.
Все сказанное здесь о периоде индукции и его влиянии на возбуждение акустических колебаний справедливо и но отношению к другим конструкциям, па прим ер пылеугольным топкам. Как уже указывалось выше, здесь тоже падо допустить существование иекоторого периода индукции, чтобы получить нужные фазовые соотношения 21 б. в. Раушеыбах между колебательной составляющей поступления пыли в зону горения и колебательной составляющей тепловыделения.
Г) Неустойчивость фронта пламепп. Эта неустойчивость, и особенно ее зависимость от ускорений, может привести к вибрационному горению. В 1944 г. Ландау показал[8]), что плоский фронт пламени всегда неустойчив и что эта неустойчивость зависит от действующих па фронт пламени ускорений. Поскольку прн вибрационном горении фронт иламепи может колебаться вместе с колеблющейся средой, он будет испытывать ускорения, которые периодически меняют знак. Периодически меняющееся ускорение приводит к периодически возникающей неустойчивости фронта пламепп, способной возбудить акустические колебания.[Вопрос этот достаточпо сложен, и его целесообразно выделить в отдельный параграф.
§ 38. Устойчивость плоского фронта пламени
Пусть в одномерном течеппи горючей смеси расположен плоский фронт пламени, нормальный к вектору скорости течения. Указанный плоский фронт будем рассматривать в качестве поверхности сильного разрыва, на которой скачком изменяются скорость течения, давление и илотиость. Поставим вопрос об устойчивости таког«!> плоского фропта пламени. Для получения связи между параметрами течепия до и после поверхности теплоподвода в стационарном процессе воспользуемся уравнениями неразрывности и импульсов
№ = №’ п8п
Если, кроме того, положить, что рассматривается течение несжимаемой жидкости[9]) (поскольку скорости Уд и i>2 малы по сравнению со скоростями звука а1 и а2), то совершенно так же, как это было сделано в § 10 при рассмотрении вопроса о тепловом сопротивлении, можно допустить, что плотпость газа ооратпо пропорциональна его температуре
Написанные равенства полностью определяют параметры тсчсппя слова и справа от плоскости теплоподвода.
Пусть стациопарное течение испытывает малые возмущения скорости и давления. Возмущения плотпостп полагаем равными нулю, так как плотность в принятой модели явления зависит только от температуры, а последняя в свою очередь от теплотворной способности смеси. Предполагая, что сгорание во фронте пламенп является полным как в стационарном, так п в возмущением режпме гореиия, получим условия Q=const для течений впереди п позади фронта пламепп.
Рассматривая устойчивость самого фронта пламени (пока никак не связанного с возможными акустическими колебаниями), введем плоскость у, z, которая будет совпадать с плоскостью фронта пламени в невозмущенном процессе. Направление оси х сохраним прежним — по скорости течеппя. Пусть малые возмущения скорости би и давления Ьр будут периодическими по времени и координате?/, т. е. пропорциональными множителю exp (i. ky — iQt) п не будут зависеть от z.
Для определения этих возмущений напишем линеаризованные уравнения Эйлера и уравнение неразрывности
Dbvx, дЬг 1 дЬр
TOC o "1-3" h z 4- 7) і = —
Ді ~ дх Q дх
Dbvv і Q§p
(38.3)
Dt ^ V дх q ді/
дх ду
Система (38.3) должна быть написана отдельно для холодной смеси и отдельно для продуктов сгорания. Индексы х ж у при 6v указывают, па какую пз осей спроектировано впзмущспце скорости. При v индексов не ставится, так как стационарное теченпе одномерно (направлено по оси а).
2і*
Продифференцировав первое уравнепие (38.3) по х, а второе по?/, сложпв их п учтя третье уравнение (38.3), нетрудно получить, что Ьр удовлетворяет уравиению Лапласа:
(ЗМ
В малой окрестности поверхности разрыва (т. е. при X Pte 0) должны выполняться некоторые условия. Рассмотрим их более подробно.
Во-первых, должпа быть непрерывной тангенциальная составляющая скорости. Пусть 6х(у; t) — малое смещение точек поверхности разрыва в направлении оси х, которое возникает при возмущепии стационарного процесса — Тогда
ДЬх v
Производная —есть тангенс угла наклона фронта пламени к оси у в рассматриваемой точке. Если этот угол обозначить а, то легко сообразить, что касательпая компонента полпой скорости выразится следующим образом;
(у 4- bvx) sin а — ь cos а.
Полагая угол а малым (порядок его малости определяется возмущением бгс), сохраним, как обычно, только члены первого порядка малости с учетом того, что для
Малых углов sm а = tg а = напишем следующее выражение для касательной компоненты скорости, справедливое в линейном приближении:
Тогда условие равенства тангенциальных скоростей с обеих сторон фронта пламени будет иметь следующий вид:
Х, дЬх с. , с?6ж /по
Ьи"л + = bvv2 + — щ — ■ (38.5)
Во-вторых, надо сделать какое-либо предположение о зависимости скорости распространения вламепи от возмущений фропта пламени. Ландау предположил, что такая зависимость отсутствует, т. е. что скорость распространения разрыва не должна претерпевать пзмене — пия при возмущении фронта. Это означает, что фронт пламени будет смещаться только возмущениями скорости, |Лё» t v v «., .
S дЬх
= (38.6)
Позже Маркштеіш1) существенно дополнил теорию Ландау, предположив, что скорость сгорапия зависит от кривизны фронта пламени, т. е. может быть связана
„ дЧх С величино и ■ — ‘«, .
В болое поздних работах появились и дальнейшие уточнения, которые здесь рассматриваться не будут.
Для целей, которые ставятся в настоящем параграфе, достаточно воспользоваться простым предположением Ландау. То новое, что вносит уточнение Маркштейна, будет вкратце рассмотрено ниже.
Условия (38.5) и (38.6) связывают возмущения скоростей по обе стороны пламенп. Для того чтобы связать и возмущенпя’ давления, необходимо ввести третье условие. Пусть па поверхность пламепи действует некоторое ускорение Ь. Тогда для брх и Ьр.1у взятых в малой окрестности поверхности раздела, можно будет записать такое равенство:
6Л-6А = 6(Є1-Є.,)б. ї. (38.7)
Как уже говорилось выше, решение уравпенпп (38.3) и (38.4) ищется в виде показательных функции, пропорциональных ехр (iky — iQl). Пусть, следовательно,
Ор — с, ехр (іку І а./ — ,-q/), 6vI = csexp(iky + CU — — iQl), } (38.8)
T>vv — cs exp (iky -f і-1′ — iQ’)>
.ос/’ У" г ks ‘є і n G., Journ. of the Aeronautical Scicnccs, № 3, и топче PJCMtB® перевод: Маркштейн, Эксиерямептальное ракетной^ Tox^lasT™ ГTf ™mC™ ФР°НТа пламмш’ Моп1">сы где а — пока неопределенный множитель. Подставив написанное здесь выражение для Ьр в уравнение Лапласа (38.4), сразу находим, что
= 0 (а>0)
Или а = ± к. Подходящее значение а можно выбрать из условия, чтобы возмущения давления, которые связаны о возмугцевпем фропта пламени, не сказывались в бесконечном удалении от фронта, т. е. при х—> ^ оо. Но тогда, очевидно, для х < 0 (холодный газ) следует выбирать flj = /c, а для х > 0 (горячий газ) д2= — А.
Помимо найденного решения, может существовать еще одно. Действительно, уравнение Лапласа удовлетворяется, в частности, прп 6/; = 0. Рассмотрим этот случай более подробно. Если положить 6р = 0, то правые части первых двух уравнении (38.3) обращаются в нуль. Подставив в них би* и bvy согласно (38.8), найдем, что для этого случая а = —. Однако, ие допуская, чтобы в бесконечном удалении от поверхности пламени (при. t—» ± со) существовали отличные от нуля возмущения скоростей 6t>x и 6і>!(, будем учитывать найденное решение лишь для горячего газа (.г>0). Это можно пояснить следующим образом. Множитель Q, который пока остается неопределенным и который можно будет найти впоследствии из характеристического уравнения, будет, вообще говори, пметь комплексное значение. При этом в случае положительной мнимой части у Q все возмущения будут с течением времени, как это видно из (38.8), стремиться к бесконечности. Для этих значений Q возмущения будут затухать с удалением от фропта пламени лишь при. г > 0. Случай, когда мнимая часть Q отрицательна, интереса не представляет, так как это будут устойчивые колебания. в то время как целью настоящего рассмотрения являются поиски неустойчивых состояний фронта пламени.
Подставив решения (38.8) в уравнения (38.3) и предполагая, что они написаны для холодного газа, возьмем а = к н подберем такие значения постоянных коэффициентов С], с2, с3, которые удовлетворяют системе (38.3). Из третьего равенства этой системы сразу следует, нто cz = ic2.
(.38.10)
Н из любого ИЗ ДІЇ ух порш. гх, ЧТО — — Q, Л’" j с…
Следовательно, коэффициенты с3 и с3 находятся с точностью до неопределенного множителя который, не нарушая общности, можно положить равным с2. Таким образом, для холодного газа решения (38.3) будут иметь следующий вид:
SPi = Л1Є1 ("X — »і) ехр (iky + k. r — iQt), j &vls = ALDxp(ilaj + kx-ittt), І <38-[10])
6vly = i’/lj ехр (iky + kx —iQt). і
Аналогично для горячего газа (учитывая, что имеется два значения а), найдем следующие выражения:
6 р., = — + — кх — iQt),
6»г:с = ехр (iky — кх — iQt) +
+ А3 ехр (iky -f — ~~~ х iQt) , 6о2в = — г А, ехр (iky — la — iQt) —
Дополним равенства (38.9) и (38.10) еще одним:
6х = А^ охр (iky — iQt). (38.11)
Последнее равенство^^говорит о том, чтр_на фр_оите пламени образовались "події и, бегущие в направлении осп у. В случае гармонических колебапий эти полны характеризуются частотой Q или периодом колебании Т — ^ ,
Ііг — — —
(38.5), (38.6), (38.7), получим систему четырех линейных однородных уравнений, содержащих четыре неопределенных коэффициента: Ах> Аг, А3 п А±. Система будет иметь нетривиальное решение при равенстве нулю определителя:
Этот определитель можно прообразовать следующим
Образом — Умножив его вторую строку на и сложив ее
С первой, иолучим определитель третьего порядка, сред-
.. — „ s2
Нии столооц которого содержит оощии мпожптель I — .
Взнося его за знак определителя, долучим:
+ 1 <к ("і —
1 0 iq =0.
Єї ("Т- —-‘V’s ‘(ЄІ-ЄІ)
Производя несложные вычисления, найдем нз этого равенства характеристическое уравнение системы:
( і+єа) + 2/£г/гол-ь
Н Ьк (еа — ei) — {Vi-Щ)] = <>■ (38.12)
= n.
Прежде всего очевидно, что характеристическое уравнение имеет корепь Q = ikv2. Однако найденный корень надо отбросить, так как в этом случае исчезают слагаемые с коэффициентом А3, указанные слагаемые становятся точно такимп же, как слагаемые с.13, и следовательно, теряются существенные свойства явления. Поэтому дальнейший анализ устойчивости поверхности разрыва (фронта пламени) будем вести прп условии
1-^гФ 0- Из (38.12) получим:
Fi2(e, + e,-H 2<Ш-р1і’| 1 W,-(p2 (.’,)-
— Л—Єії’і (fj — г’з) = о. (38.13)
Введем для удобства ІІ, — — iQ. Тогда вместо урав — ненпя (38.13) можно панпсать:
Щ (Єї + Єї) + 2аі»Єіиі — ІІІЄі — Єї) — і
+ = (38.14)
Проанализируем полученное выражение " более подробно. Пусть ї = 0 (т. е. на фронт пламени не действует ускорение). Тогда, в силу того, что v2 > t»3 (скорость течения продуктов сгорания выше скорости притока свежей смеси), свободный член квадратного (относительно Qj) уравнения отрнцателен и, следовательно, оба корня вещественны и имеют разные знаки. Следовательно, переходя к Q, можно утверждать, что движение поверхности разрыва характеризуется двумя мнимыми «частотами» £2, имеющими разные знаки, т. е, движение будет иметь неустойчивую составляющую. Таким образом, если принять допущения Ландау, получается вывод о неустойчивости всякого плоского фропта пламени.
Как уже говорилось выше, Маркштенн уточнил теорию Ландау, введя вместо условия (38.G) другое, которое учитывает зависимость скорости сгорания от кривизны фронта пла_ме_пд. В результате уравнение для определения становится несколько более сложным, чем (38.13), и его аиалнз показывает, что неустойчивость становится Функцией числа к, однозначно связанного с дливой вол-
2л
Ны возмущения на фронте пламени X — у. Прп этом удается показать, что если локальная скорость сгорания увеличивается с уменьшением положительного локального радиуса кривизны фронта пламепп1), то для достаточпо
Кривизна считается положительной, когда фронт пламени выпуклый по направленню горящего газа < 0.
Малых X процесс всегда будет устойчивым, для достаточно больших X оп неустойчив, а для Я=оэ нейтрален. Из сказанного следует, что существует некоторое значение Я=Яшах, при kotopomj процесс максимально’ неустойчив.
Если счптать, что пменно этот внд неустойчивости проявится в опыте, то следует ожидать появления на плоском фронте пламени воли, имеющих длину, соответствующую Хтоах-
Маркштейн провел серию тонких экспериментов, в которых показал, что такие волны действительно образуются и приводят к так называемой ячеистой структуре фронта пламени. Скоростная киносъемка обнаружила, что фронт пламенп как бы распадается на ряд ячеек, выпуклостью направленных в сторону свежей смеси. Ячейки все время находятся в беспорядочном движении, причем большие ячейки увеличиваются за счет маленьких и расщепляются при достижении чрезмерной величины. В результате происходит известная нивелировка размеров ячеек, и можно говорить об их средней величине. Оценка, произведенная Маркштенном, показала, что размер этих ячеек не противоречит предположению о связи их характерной величины с длиной волны А, П1ах.
Все то, что до снх пор говорилось, относилось к тому случаю, когда 6=0, т. е. на фронт пламени не действуют ускоренна.*
Достаточно взглянуть на уравпепне (38.14), чтобы убедиться, что в зависимости от знака b ускорение может оказывать стабилизирующее плп дестабилизирующее влияние па процесс. Если b < 0, то предпоследнее слагаемое в (38.14) будет отрицательным (так как вследствие нагрева q2 < q,) и, следовательно, увеличится абсолютиая__велпЧ1ша отрицательного свободного члена квадратного уравнения (38.14), что приведет к увелпче — нШо"а5сошотной величины отрицательного корня порождающего неустойчивость. При b > 0 будет наблюдаться обратная тенденция.
В опытах Маркштейна труба, в которой производилось сжигание заранее подготовленной с. меси воздуха с различными углеводородами, стояла вертикально, причем так, что холодный газ (свежая смесь) был внизу, а продукты сгорания в верхней части трубы. Следовательно, на фронт пламени действовало ускорение силы тяжести b=g. В силу действии этого ускорения, соответствующего b > О, процесс должен был стать более стабильным, чем если бы труба располагалась горизонтально.
Надо сказать, что как неустойчивость фронта пламени в смысле Ландау, так и связанная с нею ячеистая структура этого фронта не имеют прямого отношения к вибрационному горению, т. е. возбуждению акустических колебапий в трубах. Для наблюдения этих эффектов нет никакой необходимости в акустических колебаниях среды. Однако если акустические колебания возникли, то опи могут оказать мощное воздействие на рассмотренный внд неустойчивости самого фронта пламени. Действительно, при акустических колебаниях, если только фронт пламени не находится в узле скорости, его будет «таскать» за собою колеблющаяся среда. При этом неизбежно воз — пикиовенпе ускорений, действующих на фронт пламени, отличных от нуля даже тогда, когда земное ускорение па него не действует (вертикальное положение фропта пламени). Поскольку ускорение, связанное с колебаниями среды, будет периодически менять знак,. постольку периодически будет усиливаться или ослабляться неустойчивость фропта иламепи.
Маркштепн наблюдал это явление экспериментально. В тех случаях, когда в его опытах возникали колебания фропта пламени как целого, скоростная киносъемка показывала, что ячеистая структура пламени имеет тенденцию к периодическому усилению п ослаблению — ячейки появлялись и исчезали в ритме вибрационного движения фронта пламени. Таким образом, можно говорить о том, что акустические колебания влияют на устойчивость фронта пламени, а следовательно, и па его структуру.
Последнее наводит на мысль о возможности возникновения обратпой связи, необходимой для возбуждения акустических колебапий. действительно, если в ритме акустических колебании происходит измепение структуры пламени, то это может привести к изменению эффективной скорости сгорания в том же ритме, что в принципе может оказаться достаточным для поддержания акустических колебаний. Эту мысль высказывают в своей работе Маркштейн и Скуайр1).
Надо сказать, что явлення, связанные с ячеистой структурой фронта пламени, вряд лн играют значительную роль нрн возбуждении акустических колебаний в промышленных установках. Эти эффекты наблюдались лишь при достаточно малых скоростях течения. В упоминавшихся выгпе опытах Маркштейна числа Рейпольд — са для потока в трубе лежали в пределах 400—600, т. е. соответствовали ламинарному режиму течения. По-вн — днмому, значительно более существенную роль пграет несколько иной эффект, к рассмотрению которого теперь можно перейти.
Если вернуться к уравнению (38.14), то нетрудно видеть, что возникновение неустойчивости на фронте пламени связано с двумя различными эффектами. Во-первых, опа может возникнуть в толі случае, когда секундный поток массы газа через поверхность разрыва отличен от нуля (QjPjt^O). Во-вторых, она может возникнуть и прп условии = 0, но только если имеет место отрицательное ускорение Ь. Первый случай рассматривался выше достаточно подробно. Рассмотрение второго совершенно элементарно. Если ql^1 = 0, то пз уравнения (38.13) получаем
Й=± j/bfe!^, (38.15)
Формулу, известную для колебаний двух тяжелых жидкостей, расположенных друг над другом. В последнем случае полагают b = g и вещественные Q (устойчивость) получаются тогда, когда q2 < Qi> т — е- верхняя жидкость легче нижней.
Указанные два типа неустойчивости проявляются различным образом. Первый из них, связанный с пересечением массой газа фронта пламенп (Qj^i =?= 0), дает ячеистую структуру пламени, подробно рассматривавшуюся Маркштеином. Как уже говорилось выше, этот вид неустойчивости возникает и при отсутствии ускорений
J) М а г 1с s t е і п С. И., S q и і г е W., On the stability of a plane Flame Front in Oscillating Flow., Journ. Acoust. Soc. Amer., 1955, v. 27, № 3.
(£=0). Что касается второго типа неустойчивости, связанного с отличием b от нуля, то для его возникновения ею иадо предполагать пересечения потоком массы поверхности раздела сред, имеющих различную температуру, она может проявиться и на поверхности, разделяющей и среднем неподвижные газы, если только ускорение будет направлено от холодного газа к горячему. Неподвижность газов в среднем говорит о том, что горение не происходит, так как последнее всегда связано с переходом холодных газов через фропт пламени, за которым они становятся горячими. Следовательно, второй тин неустойчивости может проявляться в чистом виде на поверхности раздела газов, имеющих разную илотиость (температуру) и подверженных действию ускорения нормального к поверхности раздела. Типичным видом такой неустойчивости является волнообразование па поверхности тяжелой жидкости под действием ускорений.
Периодически изменяющие свой знак ускорения, которые могут действовать на фронт пламени при акустических колебаниях, неизбежно вызовут волпообразование па поверхности раздела (фронте пламени). Указанное волпообразование будет взаимодействовать с явлениями, приводящими к ячеистой_с. труктуре пламени, однако, если попытаться оцепить этн два вида неустойчивости с точки зрения их обратного влияния па акустические колебания, то волпообразование надо будет признать более важным. Последнее связано главным образом с тем, что периодически увеличивающееся и уменьшающееся волнообразование ведет к периодическому измепецпю интегральной поверхности раздела (площади фронта пламени) и, следовательно, к периодическому изменению эффективной скорости сгорания.
Чтобы проследить это явление в чистом виде и получить простые формулы, проанализируем устойчивость поверхности раздела при = = 0. Качествеїшо картина не изменится, если взять i»! и v2 отличными от нуля, по это нзлпшпе усложнит анализ. Для того чтобы рассмотреть устойчивость поверхпостп раздела под действием ускорения Ь, имеющего периодическую составляющую, уже нельзя воспользоваться формулой (38.15), получеппоп в предположении b = const, а весь вывод нужпо повто-
рить заново. Поскольку условия па поверхности раздела являются теперь функциями времени, решение системы (38.3) следует искать не в виде (38.8), а в более общей форме, в внде произведения пока неопределенных функций времени F (t) па множитель охр (//.’/у ах).
(38.16)
Итак, пусть
Бр = F1 (t) ехр (iky + ах),
= Fi w. exp №/+ ах):
= F3 (t) cxp (iky + ax).
Подставив bp в уравнение (38.4), получим, как и ранее, а — Ч^ к. причем выбор знаков к сохранится: для х < 0 а1 = к, а для х > 0 а., = — к.
Для холодного участка газа (х < 0) подстановка значений переменных (38.16) в систему (38.3), с учетом того, что v = 0, даст следующие соотношения между U). F,_(t) п Fs(ty.
—F 1
* (38.17)
F„ = U’. )
Обозначив (t) = At (t), можно записать: при х < 0
— — f-4(*)exp(%+/№), i 6vu = AL(t)exV(iky + kx), (38.18)
6Yi„ = іЛі (t) MP (% +J
Для горячого газа (x > 0) пз совершоппо аналогичных соображений получим:
6рг = ^ЛІ(1)ехр(іку-кх), | &v^ = A2(t)exp(iky-kx), j (38.19) 6иг,( = — (f) ехр (іку — кх). |
Соотношения (38.18) и (38.19) являются более общей записью соотношений (38.9) и (38.10), правда, для случая, когда Dj = и3 = 0.
При сравнении выражений (38.10) и (38.19) бросается її глаза отсутствие во второй группе выражении слагаемых с множителем Л3. Это связано с тем, что при = 0 = Действительно, решение с А3 было получено выше как решение, удовлетворяющее первым двум уравнениям (38.3) при бр = 0. Здесь в силу того,
Что у = 0» будет — 0 и = следовательно, функции F. z(t) и Fz (t) в формулах (38 Л 6) являются постоянными. Если они отличны от нуля, то должно существовать некоторое отличное от нуля и постоянное во времени возмущение bvx и bv вдоль координаты сс, которое в рассматриваемой задаче отсутствует. Следовательно, постоянные F2 и Fs равны нулю н слагаемые с А3> отличным от нуля, в решении появиться не могут. Дополним, как и выше, равенства (38.18) и (38.19) еще равенством
Б $ = AA(t)&xpifoj, (38.20)
Являющимся более общей записью выражения (38.11).
Обратимся теперь к формулированию условий, которые должны выполняться на поверхности раздела (при. i; = 0). Поскольку теперь необходимо связать лишь трп функции — А1 (£), Л2(г) и j44(f), — одно из четырех условии (38.5), (38.6) и (38.7) является лишним. Легко сообразить, что это условие равенства тангенциальных скоростей (38.5), поскольку прп y1=i’2 = 01 т. о. прп отсутствии пересечения средой поверхности раздела, оно теряет физический смысл.
Подставив зпачения переменных (38.18), (38.19) и (38.20) в условия (38.6) и (38.7), сразу получаем
(38.21).
= 0,
— 4" (Єі4 + — Me, — Qs) ^
Откуда следует дифференциальное уравнение для определения Ах.
(38.22)
Полагая к = ~, где Я—длииа волны на поверхности раздела, н считая, что прп акустических колебаниях поверхность раздела целпком смещается вдоль оси х вместе с колеблющейся средой по синусоидальному закону
H = h(jo, os(iit (38.23)
(// — смещение среды, о» —размерная частота акустических колебаний [1/сея]), получпм следующую форму записи уравнения (38.22):
-*1"(г) -f т ItS " и2/’«008 м) А=0′ {ЖЩ
Здесь Л = /lj, b ~ gx — <srhQ cos 0)t, причем под gx понимается проекция ускорепия сплы тяжести па ось х, взятая с обратным знаком.
Для вертикальной трубы gx совпадает с полным ускорением силы тяжести g, для трубы с горизонтальным направлением оси gx = 0. Второе слагаемое b получено двукратным дифференцированием выражения для /г.
Если ввести независимую переменную z = (ot, то уравнение (38.24) сводится к известной форме уравнения Матье:
Л" (z) + (а — 2q cos 2z) A (z) = 0, (38.25)
. — qs)
Где
1 я mqi+ft) Как известно из математического анализа, решение линейного дифференциального уравнения этого типа имеет впд
Л(г)=С1ев7(г) + Сае-в7(-г), (38.26)
Где s — некоторая постоянная, а / (г) — периодическая функция с периодом л, или 2к.
Из решения (38.26) видно, что любому вещественному s, отлнчпому от нуля, соответствует неустойчивость, так как вне зависимости от знака s, в одном пз слагаемых (38.26) эксиопенцпальная функция будет иметь положительный показатель, пропорцпопальнып времени (пропорциональный z). Устойчивости соответствуют ЛИШЬ МІШ- мые значения s.
Будем далее рассматривать горизонтальную трубу, т. о. положим дх=0, а следовательно, а — О. Если изменять параметр q так, чтобы ои пробегал положительные значения, начиная от пуля, то так называемый характеристический показатель s, равный при q —0 пулю, станет при возрастании q сначала мнимым, затем при ^=0,91 вещественным и отличным от пуля, прп (7=7,5 стапет вновь мнимым, затем почти сразу вещественным, вплоть до 1, п т. д. Следовательно, но мере увеличения q
Будут чередоваться области устойчивости и неустойчивости, причем области устойчивости характеризуются крайне малыми отрезками на оси q, в то время как области неустойчивости являются весьма протяженными. Таким образом, неустойчивость будет наблюдаться практически всегда.
Подробное рассмотрение вопросов, требующих применения теории уравнений типа Матье, здесь приводиться ие будет. В § 49 будет дапо решение рассматриваемой здесь задачи в несколько упрощенной постановке, позволяющей иолучпть его в элементарных функциях.
Для дальнейших выкладок необходимо еще указать, что первая пз названных областей неустойчивости 0,91 <q< 7,5 характеризуется периодом функции /(z). входящей в решепие (38.26), равным 2я. Следующая область неустойчивости 7,5 < q < 21 будет соответствовать функциям / (а) с периодом л, затем прп 21 < q < 42 функция /(z) будет вновь иметь период 2я и т. д. (написанные неравенства являются приближенными, кроме того, в них не учитывается, что между областями неустойчивости лежат узкие интервалы значений q, при которых поверхность раздела устойчива).
Поскольку возможна двоякая периодичность решения (38.26), а для того чтобы неустойчивость поверхности раздела (фронта пламени) могла сыграть роль механизма обратной связи, надо чтобы эта периодичность находилась в должном соответствпп с периодом акустических 22 в. в. Раушенбах колебапий, рассмотрим вопрос о соотношениях между периодами.
Период акустических колебаний газового столба есть = Если перейти к независимой перемеипой
Z = то период акустических колебаний будет
2ак = я. Поэтому решепия (38.213) в тех областях значении q, где период /(z) равен л, будут соответствовать колебаниям поверхности раздела (фропта иламепи) с частотой акустических колебаний, в то время как в других областях зпачепий q, где период изменения функций f(z) равеп 2л, период колебапий поверхности раздела будет в два раза больше периода акустических колебаний.
Нетрудно сообразить, что для возможности возникновения механизма обратной связи,"основанного на колебаниях поверхности раздела (фропта пламени) иод действием акустических колебаний, необходимо чтобы период колебаний поверхности раздела был в два раза больше акустического. Действительно, это видно из следующих простых соображений. Увеличение, вследствие волнообразования, общей площади поверхности раздела ведет, как известно, к увеличению эффективной скорости распространения пламени. Чтобы эффективная скорость распространения пламени изменялась в ритме акустических колебапий (а это иеобходимо для возникновения обратной связи), надо, чтобы период колебаний поверхности пламени был бы в два раза больше периода акустических колебании, поскольку площадь поверхности раздела (фропта пламени) будет увеличиваться как при выгибе ее в положительном, так и в отрицательном направлении оси х. Для большей наглядности соответствующие схемы приведены на рпс. 75. Слева приведен случай, когда периоды акустических колебаний (переменная Ьр) и колебаний поверхности раздела (переменная Ьх) совпадают. Тогда период изменения площади поверхности раздела 6s оказывается вдвое меньше акустического. Справа на том же рисунке приведен случай, когда период колебаний поверхности раздела превосходит период акустических колебании вдвое; изменение 6s происходит в этом случае в том же ритми, что п изменение bp, а это открывает возможность для возникновения механизма обрат — ион связи.
Таким образом, не все области неустойчивости, полученные нри анализе уравнения (38.25), представляют лп — терес с точки зреппя взаимодействия с акустическими колебаниями; существенными в этом смысле надо нрпзпать
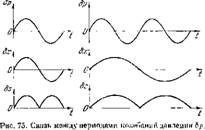
Смещения 6х и иозму щепля поверхности пламенп 6s.
Область зпачений q, определяемую неравенствами 0,91 <
Q < 7,5, затем область 21 < q < 42 и т. д., т. е. области, для которых нернод функции f(z) равен 2п.
Если сравнивать между собой интервалы значений q, для которых период функции / (z) равен 2я, то наибольший практический интерес представляет интервал 0,91 <
<7 < 7,5, характеризуемый наименьшими значениями q. Это следует нз таких соображений. Величина
Пропорциональна отношению ~. Длина волны возмущения поверхности раздела X связана с размерами сечения трубы, в которой происходят колебания, п, еслп не рассматривать очепь высоких гармоник, имеет порядок характерного лилейного размера этого сечения. Если
22*
Считать, что порядок величины X известен, то первая область значений q будет соответствовать наименьшим амплитудам hQ. Оценим порядок этих амплптуд. Прп
0,91 <q< 7.5 и подогреве, характеризуемом J-1 = 6, для
Уг
~ получим следующие неравенства:
0,1 <0,83,
В то время как для ближайшей подходящей области значении 7, лежащих в интервале 21 < q < 42, будем иметь
2,3 < ^ < 4.7.
Приведенные числа достаточпо убедительны сами во себе. Для реализации неустойчивости, соответствующей второму интервалу значений q, смещения среды при акустических колебаниях должны в 2—5 раз превосходить длины волн, образовавшихся па поверхности раздела.
Совершепно очевидно, что значительно более вероятна реализация колебаний с меньшими амплитудами /г0, соответствующими первому интервалу значений q. Кроме того, можпо привести еще такое соображение. Если рассматривать процесс парастанпя колебаний, мыслеиио увеличивая h0 от нуля, то первой подходящей областью значений q, которая встретится, окажется интервал 0,91 < q < 7,5. В то же время переход ко второй области будет затруднен, так как в промежутке лежнт область 7,5 < q < 21, в которой поддержание акустических колебаний рассматриваемым механизмом обратной связп невозможно.
Выше уже говорилось, что полученные результаты приближенно справедливы и для случая горения, т. е. для режимов, характеризуемых отличными от пуля z>, и v2. Поэтому свяжем колебания поверхности раздела с возмущениями эффективной скорости распространения пламени. Как видно из формул (1С.5) н (16.7), возмущение скорости распространения иламепи 6U определяется равенством
6*7= — TS’MO-St’- (38.28)
Изменение объема горячих газов складывается
Пз смещения фронта пламени скоростью течения v, что за время dt при поперечном сечении трубы, равном F, составляет Fvdt, и перемещения фронта пламени по частицам газа (вследствие горения) на величину SUudt, где S — суммарная площадь фронта пламени (вообще говоря, искривленного), a Uн— скорость распространения элемента фронта пламени в направлении, нормаль — пом к его поверхностп.
В установившемся режиме, когда фронт нламеии неподвижен относительно стенок, Fv—SUn=Q. Следовательно, в возмущенном движении Fr(Ј) изменится за время dt на
(F6v+UB6S + S6UB)dt. Если считать величину Ua постоянной, то последнее слагаемое в написанной сумме обратится в пуль. Во многих случаях это предположение в первом приближении можно считать справедливым, поэтому ниже будем считать, что
^JlM^fbv+U» 6Л
Подстановка этого равенства в (38.28) дает следующее выражение для возмущения эффективной скорости сгоранпя:
Т = (38.29)
Напомним, что увеличению абсолютной величины эффективной скорости сгорания соответствует смещение фронта пламени в сторону холодной смеси, т. е. в отрицательном направлении оси х.
Еслп продолжать рассматривать плоскую задачу возмущения фронта пламенп, то площадь поверхностп фронта пламени (при единичной протяженностп в направлении оси z) будет прямо пропорциональна высоте волн, образовавшихся на поверхности раздела, т. е. пропорциональна абсолютной величине 6а’, которое выражается форму — лой (38.20). Как было показано несколько выше, величина Л4 может, нри известных условиях, колебаться с периодом, вдвое превосходящим период акустических колебаний, а тогда абсолютная величина Ai будет изменяться во времени с тем же периодом, что и акустические колебания. Разлагая в этом случае разность — |6^|ср в ряд Фурье и отбрасывая высшие гармоники разложения, можно написать, что
| Ьх | — | бл [ср — Bj sin (lot + ф), (38.30)
Где | Ьх | ср — средняя абсолютная велнчииа Ьх при заданном положении рассматриваемой точки по оси у *).
Но тогда величина будет колебаться около некоторого среднего значения ио аналогичному закону:
6S = В2 sin (tot ср). (38.31)
Таким образом, возмущение эффективной скорости распространения пламенп 6U (38.29) также будет изменяться с частотой акустических колебаний. Это говорит о том, что обратная связь замкнулась: акустические колебания среды (точнее, связанные с ними ускорения) привели к периодическому волнообразованию иа поверхности пламени. Это волпообразование привело к пульса — циояному — с частотой акустических колебаний изменению эффективной скорости сгорания, что, как известно из гл. IV, при должных а ми л нт у дно — фазовых соотношениях снова дает акустические колебания.
В настоящей главе, посвященной поискам возможных механизмов обратпой связи, нет пужды уточнять фазу ф в формуле (38.31). Достаточпо того, что показана принципиальная возможность самовозбуждепия акустических колебаний вследствие деформации фропта пламени при колебаниях среды. Более подробно задача о реализации такого вида самовозбуждения будет, как уже говорилось, решена в § 49.
В заключение следует обратить внимание на одну особенность рассмотренного механизма обратной связи. Вдлнообразоваипе_ па_ поверхности пламени является типичным процессом параметрического резонанса: вследствие периодичност и существенпого параметра системы (в__рассматриваемОіі случае ускорения) происходит воз-
1) На самом деле явление будет несколько сложнее, так как А 4 включает в качестве сомножителя показательную функцию времени, бужденпе колебании поверхности фронта пламени. Возбуждение таких колебании может вести к возрастанию амплитуд волнообразования на фроите пламенп без того, чтобы возрасталп амплитуды акустических колебаний. Таким образом, обратная связь рассматриваемого тппа, в известпом смысле, сложнее тех, которые описывались в предыдущих параграфах. Это накладывает определенные трудности на строгое рассмотрение задачи в целом. Более полное изучение этого вопроса выходит за рамки настоящей книги.
ГЛАВА ЛІЗІ
РАСЧЕТ АВТОКОЛЕБАНИЙ С УЧЕТОМ НЕЛИНЕЙНЫХ СВОЙСТВ ЗОНЫ ТЕПЛОИОД ВОДА
§ 39. Общая характеристика автоколебаний
Выше уже неоднократно говорилось, что вибрационное горение и другие аналогичные процессы являются типичным прнмером автоколебаний. Это проявляется, в частности, в том, что вибрационное гореине возникает впезаппо, казалось бы, без какой-либо видимой причины. В момент, когда необходимые условия созрели, амплитуды колебаний совершают резкий п практически мгновенный скачок. Последнее хорошо видно, например, на рис.76, где приведены средние значения амплитуд колебаппй давления в дозвуковом потоке воздуха, колебания в котором были возбуждены горением. График на указанном рисунке построеп в виде зависимости отношения амплитуды колебаний давлення bp в некотором сечении потока к амплитуде колебаний, характерной для нормального (спокойного) горенпя б/?н в том же сечении от коэффициента избытка воздуха а. Опыт, результат которого приведен на рис. 7G, сводился к тому, что после поджигаиия горючей смесп производилось постепенное обогащение смеси (уменьшение а), при этом, по мере обогащения ее, регистрировались амплитуды колебаппй давления в некотором сечении трубы. Из приведенного экспериментального графика видно, что в некотором диапазоне изменения а (от а=2 до а=1,38) никакого измененпя амплптуды колебаний давления не происходит. Затем прп почти незаметном изменении а от 1,38 до 1,34 наблюдается внезапное. скачкообразное увеличение амплптуды в пять раз.
При дальнейшем уменьшении а эта амплитуда практически не меняется. Помпмо скачкообразного измепеиия амплитуд, переход через a=sl,38-~l,34 сопровождается также изменением характера самих колебаний: если при a>i,38 колебания неопределенны и изменчивы п имеют составляющие самых различных частот, то при а< 1,34 наблюдаются совершенно четкие колебаиня, составленные __ л
J 2
I
I
А-
Горения
Рве. 76. Изменение относительной амплитуды колебаний давления при вереходе к вибрацпонвому горению.
Одной или иногда двумя гармоииками, характерными для акустических свойств трубы в делом. Оба типа осциллограмм приведены па рис. 68.
Такое поведение колебательной системы можно объяснить следующим образом. Прп а>1,38 система устойчива и наблюдающиеся колебания давления являются следствием турбулентности течения, возмущепий давления, связанных с горением и т. д. Где-то между а=1,38 и а=1,34 система становится колебательно-неустойчивой по отношению к малым возмущениям; амплитуды тон гармоипки, которая стала неустойчивой, начинают быстро возрастать, и она вскоре становится доминирующей. I ост амплитуд ставшей неустойчивой гармоникп приостанавливается явлениями, связанными с нелинейными свойствами системы, речь о них будет идтп ниже.
Поскольку темп увеличения амплптуды колебаппй неустойчивой гармошши достаточно велик (обычно она достигает установившегося значения за 2—3 колебания, т. е. за малые доли секунды), то переход от нормального горения к вибрационному происходит практически мгновенно.
Как известно, линейная теория способна ответить на вопрос об устойчивости системы, но фактическое вычисление амплитуд автоколебаний в рамках линейной теории невозможно. Очень часто амплптуды автоколебаний интереса не представляют и вычисление их излишне. В подобных случаях можно ограничиваться линейной теорией. Таковы, в частности, требования к теории в тех случаях, когда автоколебания недопустимы. Действительно, еслп вибрацпопное горение пе должно возникать (так как оно грозит разрушением топки пли двигателя), то достаточно решить задачу об устойчивости процесса, а затем следить за тем, чтобы параметры системы не выходили из границ устойчивости. Другое дело, если автоколебания являются рабочим режимом, как, например, в топках с вибрационным сжиганием горючего. Тогда вычисление амплитуд является обязательным. Конечно, это не единственный случай, когда требуется знаппе амплитуд автоколебаний; оно может оказаться полезным и тогда, когда надо предварительно оцепить величину амплитуд, чтобы решить вопрос о допустимости автоколебательного режима работы установки. Короче говоря, могут представиться случаи, когда расчет амплитуд автоколебаний будет необходим, т. е. будет необходимо учитывать такпе свойства колебательной системы, которые не могут быть описаны линейными соотношениями; этп свойства будут для краткости называться далее существенными пелннепностями.
Из большого числа пелнпейных процессов, сопровождающих вибрационное горение, следует выделить наиболее важные, опустив другпе, чтобы излишне пе затруднять решепие задачи. Потери с нелинейными характеристиками можпо локализовать тремя способами. Во-первых, они могут быть распределены вдоль осп течения (трепне и потери, связанные с нелинейностью уравнений гидромеханики). Во-вторых, они могут быть связаны с излучением энергии из концов трубы; соответствующее условие может быть дапо в виде зависимости акустических имнедан — цев на концах трубы от амплитуды колебаний. Наконец, можно предположить, что процесс тепловыделения (горения) при достаточпо больших амплитудах колебаний существенно отклоняется от представляемого линейными соотношениями.
Внимательный анализ опытных данных показывает, что в огромном большинстве случаев можно с полной определенностью говорить о доминирующем значении иелппейиогтей, свойственных процессу горения. Поэтому в настоящей главе будет рассмотрен только этот случай. В то же время применяемый ниже метод может быть легко распространен на более широкий круг задач.
В предыдущей главе былп приведены многочисленные примеры механизмов обратной связи, способных привести к самовозбуждению колебательной системы. Коп — кретньтй ход решения задачи, конечно, зависит от того, какой из этих механизмов обратпой связи рассматривается в ней; однако общая методика решения ие будет претерпевать существенных изменений при переходе к другому механизму. Поэтому хотя приводимое ниже решение и опирается на один конкретный механизм обратной связи, его следует рассматривать как иллюстрацию применения общего метода. Выбор механизма обратной связи лля помещенной ниже задачи был сделан таким образом, чтобы результаты расчета можно было сравнить с опытными данными



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике