Выше уже указывалось, что численный анализ кон­кретных случаев является почти единственным методом изучения задач, рассматриваемых в настоящей главе. Однако в некоторых случаях оказывается возможным аналитическое рассмотрение. Такой задачей является, в частности, исследование колебательной системы при полном поглощении энергии падающей акустической вол — ІШ на одпом из концов трубы.

Пусть в концевом сечении Трубы с координатой (рнс. 22) нмпеданц отверстия известен и равен zv На дру­гом конце трубы с координатой |2 пусть происходит пол­ное поглощение энергии подходящих к акустических волн. В таком случае краевое условие для конца с коор — дипатоп |2 будет:

Z2=l.

Действительно, если перейти к переменным и, W, то формула (30.5) дает: при z—1 £=0. Но тогда из равенств (30.3) следует, что w=0 при ифО. Во второй главе гово­рилось, что величины w и и представляют собой акусти­ческие импульсы, движущиеся по потоку (и) п против потока (ш). Таким образом, при z2 — получается, что движущийся по потоку отлігчпьій от нуля акустический импульс и при взаимодействии с правым копцом (£ = £2) дает отраженный импульс w пулевой интенсивности. Это и говорит о полном поглощении акустической энергии у конца с координатой £ = £2.

Подставив z2 = l в характеристическое уравнение (31.4), сразу получаем его частпый вид, соответствующий рас­сматриваемой задаче:

Ехр ( ~гг_ в/Л — -(*1-И) (0і2-д«+аіі—в*і) По м VI-MtVxJ («1-1)(вм_в, в-в11+вв1) ■ W.1)

Прп заданноді процессе в зоне горения (заданных ЬЕ и ЬХ, т. е., в конечном итоге, при заданных ац, fli2′ «2і» «га) правая часть уравнения (33.1) полностью опре­делена. В общем случае вычисления дадут некоторое комплексное число А-тВі. Тогда вместо (33.1) можно панисать:

ЕхР ( i_2]/| v/i) [ cns (о} і + 1 siri и)/1 ] = + BL

(33.2)

Приравнивая вещественные и мпшшо части, сразу находим:

І —М д. и 0) = -^- Arclg —

(33.3)

Не все частоты to, даваемые первой формулой (33.3), являются решением. Очевидно, что пз множества частот следует выбрать то, для которых величина cos [ Arctg j имеет тот же знак, что п число А, поскольку величина exp vhможет быть лишь положительной.

Относительно полученного здесь решения уместпо сделать ряд замечаний. Расстояние 1£, на которое удале­но от зоны горенпя сечение, где происходит полное погло­щение колебательной энергии, пе оказывает никакого влияния на решение. Результат этот понятен, поскольку в сечении £2 гасятся все волны, идущие из зоны горения, и отраженных волн не возникает. Поэтому справа от плоскости подвода тепла 2 существуют лишь волны, бегущие в положительном направлепин оси С этой точ­ки зрения наличие справа от плоскости 2 сечения с пмпе — данцем эквивалентно бесконечной протяженности

Трубы в положительном направлении. В этой связи может показаться пеожиданным существование собственных час­тот, даваемых первой формулой (33.3). Как известно, стоячие волны, типа описываемых решением (33.3), возникают благодаря палнчию последовательности отра — же пий акустических импульсов от обоих концов трубы, Б рассматриваемом случае краевое условие %= 1 экви- иалептно иолубескоиечпоп трубе, в которой отсутствуют волны, отраженные от правого конца. Стоячие волны все же возникают потому, что вторым краевым условием но сути дела являются условия взаимодействия акусти­ческих волн и процессов в зоне теплоподвода. Дело в том, что подходящие к зоне теплоподвода волпы ие только проходят ее, но частично и отражаются. Кроме того, колеблющийся под действием падающих волн процесс теплоподвода способен сам порождать акустические волны, распространяющиеся в обе стороны. Этп отраженные п генерированные волны возвращаются к сеченшо и, таким образом, между левым концом трубы и з о пой теплоподвода существуют оба типа волн — как бегущие в положительном, так и бегущие в отрицательном направ­лении. Их взаимодействие и приводит к образованию стоячей волпы. Этим обстоятельством объясняется также тот факт, что собственные частоты зависят лишь от рас­стояния 1и значения Мь имнеданца z, и от свойств плоскости теплоподвода І1.

Возппкает естествеппый вопрос: может лп подобная система возбуждаться, т. е. могут ли существовать такие условия на которые дадут v>0?

Чтобы ответить на этот вопрос, упростим несколько задачу, предположив, что в сечепии расположен узел давления пли скорости (z1=0 ИЛИ 2г = Со).

Из решения (33.1) видно, что эти два случая отличают­ся лишь знаком правой части решения. Обращаясь к формулам (33.3), легко заметить, что указанное отличие приведет лишь к изменению частот колебании, но не может изменить велпчипы v. Поэтому оба случая будут рассматри­ваться совместно, причем для определенности будет по­ложено 2^ = 00. Этот выбор краевого условия на левом конце труоы диктуется также тем, что известны опыты, на которые ниже будет сделана ссылка, позволяющие сравнить получении© теоретическое решение с экспорilmph — том. Чтооы лайтн чпс;ю

Л-f Ві =

Обратимся к формулам (32.1). После подстановки значе­ний коэффициентов аи, а12, а21, а22 получим:

V^-M)-^1) A + Bi= .

Рассмотрим, как это делалось и в предыдущей главе, два элементарных процесса в зоне теплоподвода. Один из них характеризуется условием ЬЕ = 0 (2/х = 0), дру­гой—условием 6Х = 0 (?/2 = 0). Выпишем значения числа А—Ві для этих случаев:

А + Вг = — (,Л = П),

—-(l’1-l)

(33.4)

Л+Ві =^ (</і = 0)-

(!/»—!)

Сравнение двух вырашеиии (33.4) показывает, что они имеют совершенно одинаковую структуру — Поэтому результаты, полученные при нсследоваппп одного случая, нетрудно перенести и на другой.

Для определенности примем, что уг — 0. Положим далее

Уг = а + Ы. (33.5)

После иесложиых преобразовании получим-.

A+Bi=lK. " 7 ^ .

(„-!_£)- + »

Обозначим для сокращения записи

Ехр( i-Щ v/i) = c — <33’6)

Тогда на основании равенства (33.2) можпо составить следующую систему уравнений, связывающую веществен-
2 , sln"l— м 1

Будем пскать линии равных v в комплексной пло­скости переменного у2 (33.5). При заданных зиачепиях 1Х и Мх для заданного постоянного v величина с тоже будет заданным числом. Пользуясь системой (33.7), можно найти значения а и Ъ, являющиеся вещественной и дшп — мой частями у2 для серии заданных v. Физически это означает нахождение таких относительных значений ЬХ, прп которых возникают колебания с наперед заданным инкрементом или декрементом v. Входящая в систему (33.7) частота со является параметром, подлежащим псключепию.

Возведя равенства (33.7) в квадрат и воспользовав­шись известным тригонометрическим соотношением

Clg2 а Н — і = — Д—, ° 1 sin2 а 1

Получаем искомое соотношение, связывающее а и Ь:

[(«-тУ^^Г-

-с[7] + + № = (33.8)

Уравпенпе (33.8) является уравнением четвертой сте­пени относительно а и Ь. Поэтому можно ожидать слож­ного вида кривой, определяемой этим уравнением в коор­динатной плоскости (а, 6). Внимательпый анализ позволяет установить, что уравнению (33.8) можно придать сле­дующий вид:

Ныо переменные а п Ь: ‘П|1

2

— 2Ь

(33.7)

Таким образом, уравнение (33.8) распадается на два квадратных, и вместо кривой четвертого порядка в пло­
скости (ґ7, Ь) полупім окружность

+ + =0, (33.9)

Положение п радиус которой зависят <д параметра с, п окружность, выродившуюся в точку ‘

(i-rf;o). (33.10)

Физический интерес представляет окружность (33.9). По определению на границе устойчивости v = 0, что на основании равепства (33.6) приводит к с=1. Но тогда (33-9) вырождается в уравнение прямой и дает

« = -£-. (33.11)

Таким образом, границей устойчивости в рассматрива­емом случае является прямая, параллельная мнимой оси и идущая на расстоянии от начала координат. Б общем случае семейство окружностей (33.9) характеризуется тем, что центры окружностей всегда лежат на веществен­ной оси (в уравнении семейства отсутствуют члены, линей­но зависящие от Ь). Дальнейший анализ полученного решения удобнее провести на численном примере.

Примем, как и в предыдущем примере, -^?=0,4. Зада­вая значення с=2,5; 1,07; 1,25; 1,0; 0,83 я 0,713 (с > 1 — неустойчивость, с < 1 — устойчивость), получігм семей­ство липли v = const, изображенное па рис. 64. Как видно из этой диаграммы, но море стремления v к — со пли 4- со *) (соответственно с—»0 н с ■—5- сс) радиусы окружностей уменьшаются, стремясь к нулю. В пределе, прп с—>0 из уравнения (33.9) получаем окружность нулевого радиуса (точку) с коордипатами (—1 4-~ ‘■> 0), а прн с —> оэ точку (1 + — ; 0). Эти точки помечены на рпс. 64 буквами Л и В. Отпосптельпо последней точки следует заметить, что она

Являете я не только предельным значением линии равно­го инкремента при v —> + со, но и удовлетворяет всем

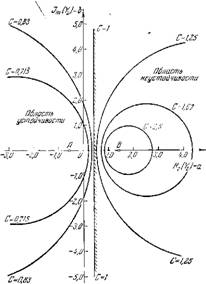
Рис, 64. Диаграмма устойчивости для случая полного поглощевия акустической энергии па одпом конце трубы.

Остальным значениям v, как это видно из сравнения ко­ординат точки В и (33.10).

Расположение границ устойчивости на рис. 64 указы­вает на то, что при 6Х=6£=0 (пачало координат) систе­ма устойчива. Напомним, что при отсутствии потерь на 18 ,Б. В. РаушснОах концах и при 6Х=ёЕ=0 она была нейтральна. Таким образом, наличие потерь, как и следовало ожидать, дела­ет колебательную систему более устойчивой/ менее склон­ной к возбуждению. /

Определим степень устойчивости системы в этом слу­чае. Воспользовавшись формулами (33.3) и (33.4) и поло­жив ^1==у2 = 0, сразу находим: 1 — М ,

СО — —jj— /сд,

Где к —О, 1, 2, 3, …; прп этом гА=0 соответствуют четные, a zx~ сс—нечетные значения к. Вне зависимости от этих значений Zj, декремепт затухания будет равен:

. т

1— М і п — i. In.

П

Как видно пз полученной формулы, степень устой­чивости процесса колебаний зависит главным образом от, точнее, от? г, так как т^ 1. Величина п равна отноше­нию скоростей звука в горячем и холодном газе и, следо­вательно, степень устойчивости процесса в рассматривае­мой системе прежде всего зависит от отношения темпера­тур горячего и холодного газа. Чем больше это отношение (чем больше? г), тем ближе процесс к нейтральному. При равенстве температур по обе Стороны 2 (т. е. при? г = 1) и при т=1 (как уже говорилось, эта величина всегда близка к единице) v —> — со.

Физически такая картина объясняется тем, что чем выше температура справа от 2, тем бблыпая доля волн отражается от 2 и тем большая доля энергии этих волн сохраняется на участке lv При /г = 1 отражения совершен­но не происходит п процесс поэтому формально бесконеч­но устойчив.

Полученное здесь решение показывает, что в принципе система с полным поглощением колебательной энергии па одном из концов трубы может возбуждаться. Оценим вероятность такого возбуждеппя. Как следует из формул (33.11) и (33.5), па границе устойчивости — • В рас­сматриваемом численном примере это приводит к необ­ходимому7 условию возбуждения |^2|>0,4. Однако при­веденная вьпне (см. § 32) оценка показывает, что подобные величины у.2 почти певероятны. Таким образом, в рас­смотренном численном примере возбуждение колебаний практически невозможно. Этот результат является типич­ным для процесса возбуждения акустических колебаний пламенем.

Интересно отметить, что полученный здесь теоретичес­кий вывод подтверждается экспериментально. В экспери­ментах Коварда, Хартвелла и Джорджей па, о которых уже была речь во введении, наряду с прочим наблюдался такой факт. Когда открытый конец трубы, в которой распространялось пламя, ничем не загораживался, то экспериментаторы получали хорошо выраженные акусти­ческие колебания со скачкообразным изменением частот колебаний, которые подробпо опнеаны выше. В тех же случаях, когда у открытого конца трубы располагалась стеклянная вата, колебания не возникали совершенно.

Стеклянную вату, помещенную у открытого конца, можпо считать устройством, полностью гасящим падающие на него акустические волпы и не препятствующим истече­нию продуктов сгорания. В теоретической схеме такому краевому условию соответствует гг = 1.

На рис. 1 ириведены записи колебаний давления, полученные в опытах Коварда, Хартвелла н Джорджсона. В верхней части рис. 1 дана запись прп отсутствии стек­лянной ваты у открытого конца трубы, в нижней части дается занпсь, полученная в тех же условиях, но при демпфировании акустических колебаний прп помощи стекляппой ваты. Приведенные кривые паглядно иллю­стрируют полученные в настоящем параграфе теоретичес­кие выводы.

Здесь был теоретически рассмотрен лишь Одни из воз­можных процессов в зоне горенпя, а именно — процесс, характеризуемый условием 6Е=(). Все полученные зако­номерности справедливы и для другого элемептаряого процесса (6.Х=0). Соответствующие формулы могут быть

Получены заменой ™ на — в выражениях настоящего

Иараграфа. Более сложные случаи {ЬЕфО; ЬХфО) можно также подвергнуть исследованию по развитой зд&Сь методи­ке, хотя они потребуют трудоемкого численного анализа. Эти случаи не анализируются, поскольку рассматривае­мая задача представляет лишь ограниченный интерес. Произведенные оценки показывают, что во всех этих случаях окончательный результат не изменится — наличие полного поглощения энергии па одном из концов трубы в снльвешпеп мере затрудняет возможпость возбуждения колебательной системы. Это обстоятельство позволяет сравнивать результаты опытов Коварда, Хартвеллд н Джорджсона, полученные ири неизвестных ЬЕ п ЬХ с расчетами, произведенными в настоящем параграфе для элементарных процессов.

ГЛАВА VII МЕХАНИЗМЫ ОБРАТНОЙ СВЯЗИ ПРИ

1 ІОЗБУ ЖД ЕЇІ И И АКУСТИЧЕСКИХ КОЛЕБАНИЙ ГОРЕНИЕМ

§ 34. Классификация механизмов обратной связи

В предыдущих главах был решен ряд задач о возбу­ждении акустических колебаний теилоподводом, причем всякий раз, явно или неявно, вводилось предположение о существовании обратной связи, т. е. об обратном воз­действии акустических колебаний на процесс горении. О большой роли, которую играет в рассматриваемом явле­нии обратная связь, уже говорилось в § 22. Чаще всего опа вводилась чисто формально, например в виде некото­рого множителя т/, связывающего возмущение скорости потока v (акустическое явлепне) с величиной ЬХ (пара­метр, характеризующий возмущение процесса горения). Иногда, как это было сделано в § 25, механизм обратпой связи описывался подробно, и тогда необходимости введе­ння такой формальпой связи между акустическими коле­баниями и процессом го реп и я не возникало.

Настоящая глава посвящается описанию различных физических явлений, через которые реализуется обрат — пая связь в рассматриваемой колебательной системе. Здесь следует сразу указать, что, как правило, между акустическими колебаниями и колебаниями процесса горения стоит целая цепочка связывающих их процессов. •!ак, например, колебания скорости течения в области расположения форсунок приводят к колебаниям коэф­фициента избытка воздуха и других характеристик смесе — ооразованпя (качество распыла горючего, траектории движения капель горючего и т. и.), а периодически измени — ющнеся свойства горючей смеси приводят к периодическим возмущениям процесса горения. В настоящем примере «цепочка» состоит всего из двух звеньев: акустические колебания возмущают смесеобразование, а смесеобразо­вание передает свои возмущення процессу горения. Вообще же количество таких звепьев может быть ii большим.

Прп объяснении механизмов обратной связи эти после­довательно связанные причины и следствия будут пи возможности подробно описываться. Однако в теорети­ческом анализе вся цепочка причин и следствий всегда рассматривается как нечто целое, как некоторый едипый механизм обратной связи.

Подробное описание механизмов обратной связи необ­ходимо по двум причинам. Во-первых, только ясное пред­ставление о физической сущностп явлепия, играющего роль обратпоп связи в том пли ином случае, позволяет «разорвать» возникшую обратпую связь и, тем самым, погасить колебания, еслп они нежелательны, или, на­оборот, стимулировать возбуждепие колебаний. Во-вто — рых, зная физическую сущность механизма обратной связи, можно описать ее аналитически и получить теоре­тическое решение задачи о возбуждении колебательной системы не в зависимости от амплитудно-фазовых соотно­шений между v, р и ЬЕ, ЬХ, а в зависимости от более «наглядных» и удобных для инженера параметров. Выше, в § 25, был дан пример доведения задачи о возбуждении акустических колебаний горением до такой формы. Задавшись некоторым конкретным механизмом обратной связи (здесь не обсуждается вопрос о том, насколько этот механизм вероятен), были получены вполне конкрет­ные выводы, например вывод о том, что система будет возбуждаться в случае достаточно крутого увеличения полноты сгорания при увеличении коэффициента избыт­ка воздуха.

Нередко авторы, работающие в области изучения вибрационного горения, ищут какую-то единственную, главную причину возникновения неустойчивости. По сути, это обьтчпо сводится к поискам главного мехапизма обрат­ной связи. Иногда это п удается для какого-либо конкрет­ного случая вибрационного горения, наблюдающегося в конкретных условиях некоторой экспериментальной установки. Однако попытка найти такой главный меха­низм обратной связи, годный для большой группы экспериментальных установок, камер сгорания двигате­лей или топок, обычпо закапчивается неудачей.

Дело в том, что на самом деле существует много раз­личных механизмов обратной связи, которые в конечном итоге приводят к колеблющемуся тепловыделению или колебаниям положения фронта пламени (или к тому и другому одновременно) и через них, как было показапо выше, к возбужденшо и поддержанию акустических коле­баний. При этом оказывается, что «главным» механизмом обратпой связи может оказаться то одип, то другой, в зависимости от конкретных условий опыта.

Ниже будет дана характеристика основных механиз­мов обратной связи. Конечпо, перечисленные ниже меха­низмы отнюдь не исчерпывают всего множества вероят­ных причин поддержания вибрационного горения. В насто­ящей главе будет дапа краткая сводка лишь тех явлений, которые на сегодпяшнпй день достаточно часто наблюда­лись и которые, видимо, играют в рассматриваемом типе автоколебаний осповную роль. Поскольку процессы горе­ния в камерах сгорания топок и двигателей связаны с процессами смесеобразования, вихреобразования и соб­ственно горепия, то и все механизмы обратной связи можно разбить на механизмы, связаппые со смесеобразо­ванием, гидромеханикой потока и собственно горением. Конечпо, эта классификация, как и другие мыслимые классификации, является весьма условной, и многие явления могут одновременно тяготеть к двум, а то и всем трем подразделениям.

Заметим здесь, что обратная связь может, вообще говоря, замыкаться и через системы автоматического регулирования, установленные на тонках или двигателях. Однако, если такие колебания, связанные с системой регулирования, и возбз’ждаются, то они обычно не явля­ются акустическими, так как быстродействие систем автоматического регулирования недостаточно для реаги­рования на акустические колебания, нередко имеющие порядок 100 и более герц. Поскольку в настоящей книге изучаются лишь акустические колебания, то колебания параметров течения и процесса горения, связанные
с работой системы автоматического регулирования, здесь рассматриваться не будут. Если же где-либо и встретится случаи взаимодействия системы регулирования с акусти­ческими колебаниями, то анализ этого процесса может быть проведен теми же методами, которыми производится рассмотрение самовозбуждения акустических колебаний теплоподводом нри отсутствии каких-либо регуляторов процесса горения или процесса течения воздуха и продук­тов сгорания но тракту топки или двигателя.

И-

Приведенную несколько выше классификацию механиз­мов обратной связи по физической сущности явлений,

Колебательная система

Обратная связь

Рпс. 65, Схематическое изображение обрат — пол связи.

Лежащих в их основе, можно дополнить классификацвей но типу воздействия обратной связи на колебательную систему. Хотя рассматриваемая акустическая система является классическим примером колебательной системы с распределенными параметрами, а современная теория автоматического регулирования рассматривает главным образом системы с сосредоточенными параметрами (систе­мы, описываемые обыкновенными дифференциальными уравнениями, а пе уравнениями в частных производных), здесь удобно воспользоваться некоторыми наглядными, схемами, применяемыми в теории автоматического регули­рования.

Изобразим колебательную систему в виде некоторого элемента, на вход которого поступают коордиваты, харак­теризующие процесс горепия ((?*, £7,, Р*), а выходными координатами являются параметры акустических коле­баний р, V и s (рис. 65). Поясним приведенную схему
несколько подробнее. Входом па рис. 65 является область горения, процесс в которой можно, как было показано в § 1(5, полностью охарактеризовать эффективными возму­щениями теплоподвода Q*, скорости перемещения фронта пламени ил и гидравлического сопротивления Iі*. Поэто­му заданием Q*, U^ и Р* задастся процесс возмущенного горения и, поскольку акустические свойства колеба­тельной системы считаются известными, величины р, о и $ для всех сечений трубы. Выходом на рис. 65 является вся масса колеблющегося газа, за вычетом зоны горепия. Следовательно, изображенную на рис. 05 схему надо понимать так: если при заданных свойствах колебатель­ной системы {Мг, М2, положение зоны горения и т. п.) задать, кроме того, п свойства возмущенного горения (Q*, UL, Р*), то тем самым будут определены и параметры акустических колебаний (;;, v и s).

Наличие обратной связи приводит к тому, что акусти­ческие колебания (выходные координаты) воздействуют на процесс горения (входные координаты). На схеме это условно изображено в виде пунктирной лннпп, ведущей от выходных координат ко входным. Хотя каждая из входных координат зависит, вообще говоря, от всех трех выходных, и поэтому следовало бы провести девять линий, соединяющих /;, и п s с каждой входной координатой, этого можпо избежать. Дело в том, что р, v п s ие являют­ся вполие независимыми параметрами, физически они представляют некоторый единый процесс акустических колебаний. Поэтому, проводя одпу линию, прп изобра­жении обратпой связи можпо говорить о том, что акусти­ческие колебаипя (как целое) воздействуют через некото­рую обратную связь на процесс горенпя (как целое). При таком подходе можно вообще пе интересоваться тре­мя входными и тремя выходными координатами, а изо­бражать одну входную и одну выходную координату. Ьдинои входной координатой будет возмущение процесса горения (имеющее составляющие Q*, Т и Р£), а выход- ноп_— акустическое возмущение (имеющее составляющие р, v и s). Для последующих рассмотрений подобный под­ход вполне достаточеп и поэтому ниже все схемы будут
изображаться одной линией. Это, конечно, не значит, что вообще нецелесообразно детализировать характер зависимости входных координат от выходных. Когда надо произвести тщательный анализ какой-либо кон­кретной обратной связи, то может оказаться необ­ходимым и более деталь­ное изучение особенно­стей зависимости каждого входного иараметра от всех выходных. Однако в настоящем параграфе та­кая детализация была бы пз лишней.

Рассмотрим особенно­сти, которыми могут об­ладать обратные связи различных тинов, харак­терные для процесса тер­мического возбуждения акустических колебаний.

Первый, простейший тип обратной связп пока­зан на рис. 66, а. Здесь выходпая координата прежде чем поступить на вход коле­бательной системы преобразуется в звене 1, которое ха­рактеризуется тем, что изменяет величины составляющих выходной координаты, преобразуя их в составляющие входной. При этом звено 1 описывается системой урав­нений вида

Q* = allp + aliV + aias,

О х = аг1р 4- a22v — f a23s,

PЈ = a3lp—a3iv + a33s,

Где коэффициенты aiv ап, аз3 — вещественные носто — яппые.

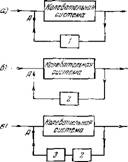
Рис. 66. Основные типы обрат­ной связи.

(34.1)

Такая обратная связь отличается тем, что составляю­щие входной координаты Q*, Uг и Р* мгновенно следуют
за изменепием составляющих выходной коордипаты р, v и s. Величины коэффициентов «п, й13, ..asa играют ири этом очень большую роль: при стремлении их всех одно­временно к нулю, обратное воздействие р, v и s на процесс — горения уменьшается и тогда естественно говорить об ослаблении обратной связи; если, например, изменить знаки всех коэффициентов линейного преобразования (34.1) на противоположные, то фазы Q*, Ul и изменят­ся на я и процесс, бывший устойчивым, может стать неустой­чивым и т. д. Этот тип обратной связи является наиболее — простым, он уже неоднократно встречался в предыдущих параграфах.

Второй тип обратной связи, по сути, близок к только что рассмотренному, он изображен на рис. 66, б. Звено 2 описывается таким же линейным преобразованием (34.1), как и звено 1, но отличается тем, что его коэффициенты являются комплексными и, в частности, могут зависеть от комплексной частоты колебаний р. Этот вид обрат­ной связи может появиться тогда, когда физические процессы, лежащие в его основе, зависят не только от р, и и s, но и от других величии, например от их производных.

Ниже будет описан процесс горения, который сущест­венным образом зависит от ускорения фронта пламени. Для него в линеипое преобразование (34.1) пришлось бы ввести

Dv

Слагаемые, пропорциональные ^ :

Тт* ~ і ~’ і — • Q = «ііV i-jf + diз* — г«14 — jr

И т. д.

Поскольку все параметры колебательной системы изменяются со временем пропорционально мпожптелю <?РТ,

Dv,—

То^=ри и линейное преобразование (34.1) приобре­тает вид

Q* = аир + (а12 + al4p) v + «13«

И т. д.

Из написанного равенства сразу видно, что коэффици­ент при v стал комплексным и перестал быть постоянной — он зависит от р.

Физически второй тип обратной связи отличается, как и первый, мгновенным следованием за изменением состав­ляющих выходной коордипаты (р, v, s), но допускает при этом дополнительные фазовые сдвиги. Действительно, умножение V па комплексный коэффициент («13-|-«14Р) означает не только изменение масштаба, но и поворот соответствующего слагаемого в комплексной плоскости.

Третий вид обратной связи изображен на рпс. 00, в. В простейшем случае оп состоит из двух последовательно расположенных звепьев — первого, совпадающего с толь­ко что рассмотренным звоном 2 (звено 1 может рассма­триваться как частный случай звена 2), п звена дающего временное запаздывание. Этот тин обратной связи реали­зуется тогда, когда процесс горепия следует за изменением р, v и s пе мгновенно, а с некоторым запаздыванием. Пример такой обратной связи уже рассматривался в § 2(j. Простейший случай, изображенный па рис. 66, в, соответ­ствует такому процессу, когда время запаздываппя Дт может быть принято единым для всех составляющих соответствующего лпнейного преобразования типа (34,1). Лить в этом случае звенья 2 и 3 можно расположить последовательно. Следует заметить, что обычно рассма­триваются лишь такие процессы. Если бы возникла необ­ходимость введения более одного времени запаздывания, например Atj, Дт2 и Дт3 связанных соответственно с р, у it s, то это не привело бы к необходимости разрабатывать какие-либо новые методы расчета колебательной системы, а только увеличило бы вычислительные трудпостл. При учете запаздывания по схеме, изображенной па рпс. 66, г?, коэффициенты линейного преобразования (34.1) становят­ся, вообще говоря, комплексными, причем все они умно­жаются на ОДИН и тот же комплексный множитель (см. § 26), зависящий от времени запаздывания Дт.

Таким образом, различные тшш обратной связи можно классифицировать по виду коэффициентов линейного пре­образования (34.1). Если они содержат мпожителем то налицо обратная связь с запаздыванием, если они

Комплексные, но не содержат времени запаздывания, то обратная связь характеризуется наличием дополнитель­ных фазовых сдвигов; если они вещественные, то налицо просгешпнй вид обратной связи. Конечно, эта классифи­кация, так же как и предыдущая, является условной п тмголпой.

("делаем в заключение настоящего параграфа несколь­ко общих замечаний.

При описании различных видов обратной связи ниже принимается, что процесс колебапий близок к установив­шемуся, т. е. что система близка к границе устойчивости. Выше уже подчеркивалось, что при решении задачи без учета начальных условий надо допустить, что процесс колебаиий происходит достаточно долго и что он в то же время ие вышел (по амплптудам) за пределы, допускаемые линейной теорией. Это сразу ограничивает допустимые масштабы неустойчивости. Одвако дело не только в таких формальных соображениях. Обычно наибольший интерес представляет мехаппзм обратной связи, который под­держивает возникшие автоколебания. Описание его есте­ственно вести для установившегося процесса колебапий. Up и таком подходе допускается, копечно, известная нестро­гость в рассуждениях. Поскольку процесс автоколебании установился, постольку явление стало существенно нели­нейным и сделанные выше ссылки на свойства линейной колебательной системы нельзя призпать достаточно убеди­тельными. Одпако, поставив себе целью лишь качествен­ное описание, можно сделать предположение, что оспов — ные физические явления, приводящие к образованию обратной связи, могут быть одинаковыми как в период медленного нарастания колебаний (линейная колебатель­ная система), так и тогда, когда колебания установились (в колебательной системе начали играть существенную роль нелинейные члены). Поэтому при анализе возможных механизмов обратной связи в дальнейшем вещду прини­мается, что колебания уже установились, и описывается цепь явлений, ведущих к поддержанию этих колебаний; при этом не делается разницы между двумя случаями — линейной системой, находящейся на границе устойчиво — ■івт’ кПлІТбЛіт"°П0" системой в режиме установившихся