В предыдущем параграфе были приведены общие решения уравнений акустики движущегося непзоэнтропнческого газа. Однако для однозначного определения исследуемого процесса необходимо сформулировать краевые и начальные условия. Эти условия могут иметь различігай впд, в зависимости от конкретного содержания задачи.
В простейшем случае краевые условия могут сводиться к линейным однородным соотношениям между переменными, которые должны удовлетворяться на концах трубы. Поместим начало коордипат | = 0 в левом конце трубы и, приняв длину трубы за характерный линейный размер L, получим для правого конца координату | =
Тогда эти условия можио записать, например, в таком виде:
Прп 1 = 0
(для всех т>0),
A2lv + ai2p + aiSs = О
«зі^ -1- я32? + «ваз = 0 лрп I = 1
Где аік — численные коэффициенты.
Задание этих соотношений не определяет, однако, задачи полностью, к ним следует добавить еще начальные условия:
« = /,(!) при т — 0, 0<£<1, р = Ш при т = 0, 0<|< I, S = /з(I) при т = 0, 0<|<1,
Где /і, /2 и /3 —задаипые функции.
Среди задач описанного типа особый интерес представляют такие, в которых два из трех краевых условий не содержат s, например в предыдущем примере случай,
когда й13 = й23 = 0. Тогда наличие двух краевых условий, содержащих только р п v, позволяет решать краевую задачу для двух первых уравнений системы (4.10) отдельно от последнего уравнения этой системы. Во многих случаях это оказывается достаточным, так как обычно наибольший интерес представляют колебания давления и скорости газового течения. Лишь в тех случаях, когда надо знать также и колебания энтропии (или других связанных с нею величии), приходится обращаться и к третьему уравпепшо системы (4.10).
(5.1)
(5.2)
Рассмотрим простейший пример — продольные колебания і; газовом потоке, текущем вдоль трубы, открытой с обоих концов. Если считать, что открытые концы сообщаются с неограниченным пространством, то в первом приближении и качестве краевых условий можно использовать часто применяемое в акустике условие постоянства давления па концах трубы, естественное для трубы в безграничном пространстве. В рассматриваемой задаче это условие примет вид
/) = 0 при £ = 0 (т>0), ] р = 0 при |=1 (т> 0). )
Напнсашше краевые условия пе содержат перемешюй о, поэтому будем решать краевую задачу для двух первых уравнений системы (4.10). Зададим еще начальные условия:
А = /іЮ при т = 0 (0<£<1), Р=Чг(I) при т = 0 (0<|<1).
Задаппе функций Д и /3 означает, что возмущение движения газа в трубе в начальный момент времени известно.
Обратимся к решению (4.13). Из формул (4.14) видно, что црп 6 = 0 q>j(0)=l, ф2 (0) = 0.
Следовательно, второе равенство (4.13) дает лрп | = 0 /> = Л;,йИт. 11о первому пз условии (5.1) эта велпчица равна нулю для всех г, что возможно только при А =0. На другом конце трубы при 1 = 1 тоже должно выполняться условие р — 0. Из (4.13) и (4.14) следует, что это возможпо
/
Лишь для /
Вторая формула (4.14) показывает, что, если отбросить тривиальный случай Д. = 0, последнее выполняется только прп
(5.3)
Пусть р является комплексной величиной р = v + ш.
Тогда (5.3) можно свести к двум равенствам, связывающим один лишь вещественные велпчпны:
Sin тіш ш ехР ( — v) =
Поскольку показательная функция веществеппой пере — меппой всегда положительна, эти два равенства могут удовлетворяться одновременно только при v = 0,
Со = (1 — Af2)foi (А = 0, 1,2, …). Таким образом, заданным краевым условиям удовлетворяют гармонические колебания с вполне определенными частотами а> (случай А" = 0 рассматриваться не будет, так как он соответствует не представляющему интереса переходу потока на новую стационарную скорость течения прп том же давлепии: р = 0, u = ^1) = const при всех х и Здесь следует заметить, что точно такие же частоты получились бы для краевых условий и = 0 на обоих концах трубы.
(5.4)
Самая низкая допустимая частота, соответствующая к = 1, o)j = (1 — М’1) ^называется основным тоном колебаний. Более высокие частоты (о2 = (1 — М-) 2л; со3 = (1 — Л/2) Зл; … и т. д. часто называют обертонами. В настоящей книге будет использовапо другое наименование допустимых частот коле баи ип. Условимся называть их собственными значениями частоты, илп гармониками. Прп это. м основной тон (нашшзшуто частоту) будем называть первой гармоникой, частоту, соответствующую к = 2 — второй гармоникой и т. д.
Каждое значение со, взятое по формуле (5.4), т. е. каждая гармоипка, определяет частное решение системы из двух первых уравнешш (4.10), удовлетворяющее постав — лешіьім краевым условиям. В силу лпнейпостп этих уравнении сумма частных решений также удовлетворяет этим уравнениям и краевым условиям (5.1).
Следонательно, решением системы будут не только функции (4.13), но и их суммы. Взяв суммы для всех значений к, получим
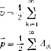
A, [Є~1 еі(і+М)Ля6] ei (1-М*) hire
(5.5)
Л=і
Здесь буквами Alfk обозначены неопределенные пока числа, которыми можпо распорядиться так, чтобы удовлетворить начальным условиям.
Строго говоря, прежде чем ндти дальше, надо было бы доказать сходимость рядов (5.5). В курсах уравнений математической физики приводятся соответствующие теоремы, которые позволяют судить о том, какие ограничения следует наложить на функцнп Д (|) н /., (|) (5.2), чтобы пх можпо было разложпть в ряд по функциям, стоящим в прямых скобках в выражениях (5.5). Этот вопрос и рпд примыкающих к нему вопросов математического характера здесь псследоваться не будут, главным образом потому, что в дальнейшем задачи с начальными условиями не рассматриваются; интересующиеся найдут соответствующие сведения в специальных руководствах.
Для полноты доведем, однако, решение поставленной в настоящем параграфе задачи до копца, сделав упрощающее допущение, что газ в трубе неподвижен (Л/ = 0).
V —
Тогда решения (5.5) примут при х = 0 следующий вид:
2 cos
P= 2 — tAvk sin



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике