Иеременные:

Чтобы проиллюстрировать метод решения задачи об устойчивости газового течения рассматриваемого типа, дадим здесь изложение схемы расчета одного из возмож­ных случаев возбуждения акустических колебаний тепло- подводом. В предлагаемом вниманию читателя примере основной следует считать имепио методическую сторону решения задачи. Что касается выводов технического или физического характера, которые можно сделать из анализа полученного решения, то опи имеют более частный характер.

(23.1)

Рассмотрим течение газа но трубе, причем будем пред­полагать, что зона переменного во времени теплоподвода удовлетворяет необходимым требованиям и уже сведена к некоторой фиктивной поверхности сильного разрыва 2. Примем те же обозначения, что и в предыдущем пара­графе, и пусть краевые условия снова будут соответство­вать узлам давления на открытых концах трубы;

Тогда, воспользовавшись решением (4.13), можно написать

ЩЧ>г (tl) + РіФі (У =■ 0,

Щ<Рг (h) + PiФі (Si) =0.

Пусть условия на 2 задали в следующей форме:

»а = ви"і+ a ls

Pi = «21У1 + a2Z

(23.2)

Ута форма записи отличается от канонической. Ее можно получить из формул (17.5), если сделать предпо­ложение, что «холодпая» часть течепия пзоэптропнчна = 0) и что характеризующие процесс нестационарного горепия величины ЬЕ’ п ЬХ’ могут быть представлены в виде

ЬЕ’ = ЬлiV, 4 bmPi, )

П- _ (23.3)

6.Х I

Напнсанпые здесь равенства опять следует тракто­вать как формальное введение некоторой обратной связи. Физический смысл формул (23.3) сводптся к тому, что процесс горепия следует за изменепиямп давления п скорости перед зоной горенпя и, в частности, при колебательном изменении рх п і (образованпи акусти­ческих волн) процесс горенпя приобретает колебательный характер. Ниже эта формальная запись будет конкре­тизирована.

Исключив с иомопц>ю (23.2) и р2 из системы (23.1), придем к характеристическому уравнению вида:

] Lo. (23.4)

I апЪ (У + °2іФі (У Й12Фз(У Т — ^22Фі (У I

Функции фі и ф2 заменим их выражениями согласпо формулам (4.14), учитывая при этом соотношение (22.5) п вводя — и h — bi ("чтобы иметь дело с положитель­ными величинами —безразмерными длинами и /2 холодпой н горячей частей трубы). После ряда преобра­зований, которые здесь опущены, получим характери­стическое уравнение системы в следующей форме1):

^ Ґ — К , 2/, , л 2/,6 .

С1 "р С таг+) Р+с[5]Ехр г=щ+

= а11 — Й12 — — f |

С4 = — — Я,2 — «21 ~ atГ

Следует подчеркнуть, что входящие R выражения (23.2) коэффициенты аи, </,„, ап, а22, характеризующие процессы в зоне горения и их зависимость от акусти­ческих колебаний, предполагаются вещественными. Тогда числа Си С2, С3 и С4 также будут вещественными и будут зависеть лишь от свойств зоны теплоподвода.

Если учесть, что р — v -(- і’со, то, подставив выражение р в (23.5) и разделяя вещественную и мнимую части, получим систему двух уравнений для определения v и о):

Cte<hi+*2)v cos (h1 + h2) Сі) + C2ehiv cos /ztw + |

4- Cae’w cos k2& + C4 — 0, Ce<hH-»e>v sin (hl — f h2) m — f C2ehiv sin /^m 4

+ Cseh*v sin h2o) = 0. J

Здесь

Нетрудио убедиться, что решение системы трансцен­дентных уравнений (23.7) в общем виде практически невозможно. Здесь будет дай графоаналитический метод решения такой системы.

Напишем систему (23.7) в следующем виде:

COS /1,03 + C3e^v cos A2Ci) = 1

— ^C.-C^+’^cosih^h,)^ C2eh^ sin h1 to — I — C*fih2V sin h2(s) = j ^ » ;

Возводя в квадрат левые п правые частп этих равенств и складывая их, получим:

Ce2h>y — Ь 2Сcos [к, — hz) (о — f =

(23.7)

= 2Cjf;4e("’ w^v tos (/?х-ь /g (o+qe2</IrH12)v

Элементарные преобразования нереводят это соотноше­ние в следующее:

[CЈe<fti-fta>v+ — CJe—<Л=

= 2 [СХС4 cos (Aj + A2)w — СгС3 cos (Aj — h%)со]. (23.10) Здесь искомые величины v и (0 находятся по разные стороны знака равенства. Пользуясь этим обстоятельством, нетрудно построить кривую, определяемую уравнением (23.10) в координатах v, ш. Для этого достаточно построить левую часть как функцию v, правую как функцию w п перенести точки, удовлетворяющие равенству (23.10), в координатную плоскость v, со.

Если рассматривать (23.9) как систему линейных неоднородных уравнений для определения величин C*ehlV и C3eh*v, то можно написать:

І — Сі — С^^1’^ cos (А, + h2) (о cos h2to |

Hav 1 I cosA^tn — C4 — C^i+^cos A2) (и I зЄ 2 ~ Л | sinAjto — C^i+b*^ sin (A, + Ajj) w [‘

Где определитель системы

I cos Aito cos А»ю ] A = , , 2 = sin (A, — Л,) оз.

I sin /^w sm A2co I

Произведя несложные преобразования, можно прпйти к следующим равенствам:

С e, ilV _ — Cj sin /*аTo + Iy(‘t] +"2)v sin ;?1to ,

Sin (Л2—-Лі) ш ‘ c _ Ct sin k1Qi—C1e(-hl+hi)v sin M

— sin (/?2—^i) co Эти равенства справедливы, конечно, лишь при условии

А = sin (А2 — Ах) со ^ 0. Перемножая соответственно левые п правые части (23.11), найдем после пекогорых упрощений

^2e2(/il+/i2)v e(/ti+b2)v х

Х ^gCasiu^B — Hi) СО —С, С4 (Sin2 Fttco + а1п»Лаи>) = Q

(23 ЛІ)

БІЛ ft-jCO SH /і20> "І" і —

Последнее равенство является квадратным уравнеппем относительно e<‘l’+,i!>v, ir следовательно,

,<„, ,„2)v = , (23,12)

Vgg

, / v _ С2С3 Sin2 {h2 — h]) la — Cfij (Sin2 /^ы-рмч2/^03) 1 ^ ‘ sin /v j со sin llt(i)

В коордшіатах v, to уравнение (23.12) определяет некоторую кривую, построение которой ироводптся эле­ментарно.

Искомые значення со и v, удовлетворяющие системе

, будут координатами точек пересечения кривых

И (23.12). Здесь следует, одпако, указать на некоторую дополнительную трудность. При получении уравнепий (23.10) и (23.12) оказалось необходимым произвести такие действия, как возведение в квадрат, почленное перемножение двух равенств. В результате система из уравнений (23.10) и (23.12) дает не только корпи системы (23.9), по ряд лишних корней, которые необходимо отделить. Отделение корней проще всего про­изводить пепосредствеппой проверкой — подстановкой найденных графически значений v и со во второе уравне­ние системы (23.7).

Приведем пример подобного расчета. Пусть =0,5, температура воздуха до подогрева 288* К, после подогрева 1500° К, а скорость холодного течепия 50 м/сек. Процессы в зоне теплоподвода примем такими, что Jx = =/2 == 0 и возбужденпе системы может происходить только за счет возмущения теплоподвода Q. Тогда лрл пе — которых фиксированных свойствах Q, которые будут ука­заны ниже, можно провести расчет по описанной выше ме­тодике.

Не приводя пнкаких численных расчетов и промежуточ­ных построений, дадпм сразу график, по которому опреде­ляются значення v и со. Как только что было показано, эти величины могут быть найдены как точки пересечения кри­вых в плоскости v, со, определяемых уравнениями (23.10) и (23.12). Обозначим первые m нпх F (v, о) — 0, а вторые / (v, (й) = 0.

Иа рис — 33 это построение дано для рассматриваемого конкретного случая. Следует лишь иметь в впду, что

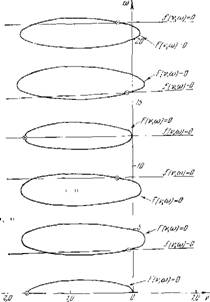
Рис. 33. Графический метод нахождения корней характе­ристического уравнения.

Ветви/(v, о>)=0, которые давали лишние корпи, па рпс. 33 опущены. Кроме того, поскольку изменение знака со на обратный не меняет системы исходных уравнений (23.7), построение сделано лишь для положительных (О. Точки ПЛОСКОСТИ V, (0, являющиеся решениями, отмечены кру­жочками. Приведенное построение представляет интерес (н является типичным) с двух точек зрепня. Прежде всего бросается в глаза то обстоятельство, что частоты колеба­ний, которые допускаются системой, отличаются от частот, определенных по привычной акустической методике. Дей­ствительно, колебания в цилиндрической трубе с двумя открытыми концами должны, казалось бы, иметь следую­щие периоды: наибольший, равный времени, необходимому для того, чтобы звуковая волна успела переместиться от входа к выходу трубы и обратно, и серию периодов, состав­ляющих г/2> 1/3, 1/4… и т. д. части наибольшего периода (см. §§ 5 и б). Если проделать такой расчет для рассма­триваемого случая, то окажется, что система должна допу­скать следующий ряд частот:

О) = 0; 4,11; 8,22; 12,33; 16,44; 20,55; … Фактически же допускаются:

А) = 0; 3,38; 9,1; 12,33; 15,7; 21,4; …

Эта особенность рассматриваемого случая объясняется следующим образом.

При прохождении звуковой волной поверхности разрыва 2 некоторая часть ее отражается и идет обратно. Поэтому элементарные соображения, приводящие к привычному акустическому правилу, Здесь неприменимы. Сложная игра преломленных н отраженных волн с учетом их отражений от обоих концов трубы дает резуль­тат, приведенный во второй строке частот со. Сравнение обеих строк показывает, что простое акустическое правило можно применять только в тех случаях, когда требуется грубая оценка частот.

Второй особенностью, выявленной приведенным рас­четом, является то, что различные гармоники затухают с различными декрементами. В рассматриваемом числен­ном примере наиболее блпзкимп к границе устойчивости (v = 0) оказались первая и четвертая гармоники. Что ка­сается апериодического члена (со = 0) и третьей гармоники, то они наиболее устойчивы. Поэтому нри сравнительно
малом изменении параметров поверхности 2 {малом изме­нении Q) наиболее вероятно возникновение колебатель­ной неустойчивости с частотами первой и четвертой гармоник.

(24.2)

Поскольку в реальных процессах высокие гармоники характеризуются при прочих равных условиях повышен­ным рассеиванием энергии, то в случае возникновения не­устойчивости рассматриваемая система скорее всего даст колебания с частотой первой гармоники (основного топа). Таким образом, проведенный расчет позволяет поннть, как колебательная система «выбирает» частоту колебании.

§ 24. Построение границ устойчивости

Приведенное в предыдущей! параграфе решение харак­теристического уравнения рассматриваемой задачи осно­вывалось на том, что процессы в зоне теплоподвода можно описать равенствами (23.3). Рассмотрим вопрос о свойствах зоны теплоподвода более подробно. Чтобы существенно упростить анализ условий возбуждения, сделаем предпо­ложение, что величины бЕ’ и ЬХ’ зависят от одного ком­плексного параметра; выше такой параметр Y уже вво­дился. Этим параметром в конкретных случаях может быть, например, возмущение эффективной линейной скорости горения Uv возмущение теплоподвода Q пли иной вели­чины, характеризующей нестационарное горение. Остано­вимся на каком-либо конкретном предположении. Пусть, например, этим существенным параметром будет возмуще­ние теилонодвода Q. Тогда равенства (17.4) позволяют написать

Сравнивая эти выражения с формулами (23.3), можно видеть, что безразмерное возмущение теплоподвода Q должно в явной форме зависеть от /Г, и vt:

<J = <lP,-vQvPv

Но тогда формулам (23.2), являющимся следствием равенств (І7-5), можно придать такой вид:

Р-2 = «і + <М Ц + («22 + <4СУ Pi — J

Здесь а’п ап … п т. д. Из формулы (24.2)

Видно, что Q полностью определяется (при заданных р{ и Uj) коэффициентами QvmQp. Раньше для определения возмущения Q бралась его амплитуда и фаза, теперь— проекции вектора Q на и vv Оба способа записи Q можпо прпмепять с одинаковым успехом. Применявшееся в предыдущих параграфах задание Q (нлн Y л т. п.) через амплитуду и фазу имеет преимущество большой общности. Однако в некоторых случаях, когда известна зависимость тепловыделения от состояния колебательной системы, бывает удобно выразить эту зависимость в яв­ном виде. Пусть, например, тепловыделение — извест­ная функция давлення и скорости

Q = Q(v1;P1)

И не зависит от пных параметров. Тогда, взяв вариацию от этого выражения и перейдя к принятой системе без­размерных переменных, можно написать

Q = C*L^ + C%§rPl, (24.4)

Где Сг и Сг — некоторые постоянные.

Сравнивая выражения (24.2) и (24.4), убеждаемся

В том, что коэффициенты Qv и Qp пропорциональны

№

И, т. е. выражают некоторую реально существующую "Pi

Зависимость тепловыделения от скорости течения и дав­ления.

Рассмотрим вопрос о границах устойчивости при за­писи свойств плоскости разрыва 2 в виде равенств (24.3). Применим для этой цели прием, использопашшй в § 19: будем рассматривать vlt рг, v2, р2 в качестве векторов s 2U построение границ устойчивости 187

И возьмем скалярное произведение равенств (24.3) друг на друга. В силу ортогональности р и v при v = 0 про­изведения pv обратятся в нуль, что даст следующую связь между коэффициентами Qv и 0L> па граипде устой­чивости:

Vl (а’и + <$„) (а’„ + a"KQ,) + р; « a"nQp) «2 + a;,Qv) = 0.

(24.5)

Для каждою заданного отношения — Ц — уравнение (24.5)

Определяет кривую второго порядка в плоскости {Qp; Qn). Все эти кривые проходят через четыре точки А, В, С и I)

(рпс. 34), координаты которых находятся приравнива­нием нулю первой и третьей, второй и четвертой н т. д. круглых скобок в уравнении (24.5), а сами кривые лежат внутри полос, ограниченных прямі, шн, параллельными осям координат и идущими через эти точки. Более подробный численный анализ показывает, что семейство кривых является семейством эллппсов, три из которых показаны на рис. 34, построенном для течений, харак­теризуемых 0,1; Л/2 = 0,25.

Изображенные па рпс. 34 эллппсы нп в коем случае нельзя рассматривать в качестве границ устойчивости. Полученные из энергетических соображений для постоян­ных-^ и, следовательно, без учета краевых условпй, эти v

Эллипсы обладают лишь одним важным свойством: точки, соответствующие границам устойчивости, могут лежать только на нолучепных эллипсах, а следовательно, только внутри или на границах вертикальной и горизонтальной ПОЛОС, определяемых ПрНМЫМИ… и Т. Д.

(или, в более короткой записи, прямыми ап = 0, а12 = 0, дй1 = 0 и ап = 0).

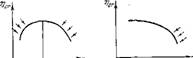
Диаграммы устойчивости для простейших случаев. Располагаясь внутри или на границах найденных полос, границы устойчивости, построенные с учетом краевых условий, могут давать различные конфигурации областей устойчивости. Покажем это для предельных случаев. Пусть длина lL пренебрежимо мала, т. е. вся труба занята горячими газами, а горе пне происходит во входном сече­нии. Тогда перед зоной горепия должно выполняться при­нятое выше краевое условие — Это сразу приводит к обращению в нуль второго слагаемого уравнения (24.5), и единственными границами устойчивости (впе зависимо­сти от величииы у-,) будут прямые ап = 0 и a2i = 0. Со­ответствующая диаграмма устойчивости приведена па рис. 35, а. Поскольку известно, что начало координат соответствует устойчивому режиму, область неустойчи­вости (заштрихованная часть диаграммы) находится сра­зу. На толі же рпсупке (диаграмма б) для полноты приве­ден случай, когда краевое условие при = 0 имеет вид

= 0 (закрытый конец). Тогда совершенно так же полу­чаем грапицы в впде равенств я12 = 0 и а22 — 0 для всех pv

Другим предельным случаем будет труба с пренебре­жимо малой длиной горячей части течения: Ь=-0. Най­дем границы устойчивости для краевого условия р. г = 0. С этой целью перепишем уравнения (23.2) следующим

Где

Д =

| а. п а22

Ооразом:

(24.6)

И иредполагается, что Д 0. Взяв, как и раньше,

О,

Агг-И

Ягг’О

П

Шгг’О

S>

А„=о

Ш.

Aj,=0~

Ш,

І% :жж

Zffp

I

I

"Т

-/А ^

Рис. 35. Диаграммы устойчивости дли предельных случаев.

Скалярное произведение равенств (24.6) друг на друга

(и и jи считаем векторами), вместо уравнения (24.5) получим:

Ъ’га21а2г + р1аиа1г = 0, (24.7)

Откуда при ^2 = 0 сразу находим границы устойчивости для произвольных v2: а21 ■= 0 н а22 — 0. Соответствующий тип диаграммы устойчивости прпведеп на рис. 35, в. В отличие от диаграмм тииа я и б, область неустойчи­вости укладывается здесь не виутрь полос, а полностью охватывает два квадранта всей бесконечной плоскости параметр о в QQn. Так же, как к в предыдущем случае, приведем для полноты диаграмму устойчивости, соответ­ствующую краевому условию Тогда для всех р2 границами области устойчивости станут прямые ап — б и а13 = 0, что даст диаграмму з) на рис. 35.

Как вндпо из приведенного примера, конфигурация областей устойчивости может в рассматриваемом случае изменяться весьма сильно в зависимости от того, каковы величины Pi, р2 и v2 в плоскости подвода тепла. Такое разнообразие конфигураций связано, в частности, с тем, что границы устойчивости могут уходить в бесконечность. Если построить аналогичные грапицы в системе коорди­нат, принятой в § 19, то случаи рх=0 и 1^ = 0 дали бы совершенно однотипные конфигурации областей неустой­чивости — окружности. Эти окружности приведены, напри­мер, на рнс. 28. Что касается случаев р2 = 0 и а2 = 0, то в системе координат § 19 построение областей неустой­чивости не дало бы столь простых границ. Дело в том, что эта система предполагает ориентировку векторов рг и г, в положительных направлениях осей координат, в то время как положение векторов рг и г>а остается произвольным. Это и ряд дополнительных трудностей делает нецелесообразный! подробное рассмотрение границ такого рода.

Использование переменных Qp и Q0 хотя п усложняет конфигурации границ устойчивости, но зато может упро­стить анализ условий возбуждения, как это будет видно из содержания следующего параграфа.

Прежде чем перейти к вопросу о копфигурацин гра­ниц устойчивости в плоскости параметров Qp, Q0 прп и /2, одновременно отличных от нуля, укажем еще па одно свойство диаграмм устойчивости, приведенных на рис. 35.

При со или Qv—> ± со декремент затухания

(или ннкремент возрастания) колебаний стремится к нулю. Таким образом, в бесконечности как бы располагается еще одна граница устойчивости. Это можно показать различными способами. Здесь будет дано доказательство этого утверждения путем анализа характеристического уравнения системы (23.7), что позволит попутно осветить еще один вопрос. Возьмем, для примера, диаграмму устойчивости, приведенную на рис. 35, в. Положив 12 = О, получим /<2 = 0 и равенства (23.7) примут крайне про­стой вид:

(C1 + C8)^cos/ilM + C3 + ^ = 0, 1

(С1 + Г2)й,,^рш/г1(о = 0. I {

Очевидно, что собственные частоты будут определяться равенством sinA1to = (); не уточняя их, заметим лишь, что при этом cos kx(i) = ±1. Так как e»Jv может быть лишь положительной величиной, то знак cos /^со будет совпадать

С-лА-СА

Со знаком отношения — >, ■ ■ , что позволяет написать

О ]_-}-(./а

V = fln I^XTH"

Воспользуемся связью (23.В) .между Clf С2! C’s п C, v с одной стороны, и аи, а12, а31 и а22, с другой, а также формулами (24.3), чтобы придать последнему равенству вид

V= 1 ln| (24 9) А, I («и—«зі)—"5i0»+<!!iQi> I ‘

Положив в (24.9) v —0 (условие существования гра­ницы устойчивости), легко найти с учетом (23.2) и (24.3) уже известные границы устойчивости «2] ■ ■ 0 и а22 = 0. кроме того, еще Qp= ± со II Q — 4- оз. Совершенно так же доказывается это положение и для других типов диаграмм, приведенных па рпс. 35.

Формула (24.9) дает возможность указать па одіто обстоятельство, которое надо всегда иметь в впду. При некоторых ^комбинациях Qv и Qtl числитель или зламе — натель дроби, стоящей под знаком абсолютной величины, .может обратиться в нуль. Этому будет соответствовать v —> + со или v —^ — со. Таким образом, рассуждая формально, можно утверждать, что где-то в плоскости параметров Qp, Qn расположены две прямые, которым соответствует бесконечно большая устойчивость или бес­конечно большая неустойчивость течения. В действитель­ности это связано с тем, что задача об устойчивости тече­ния рассматривается здесь, как и везде в данной книге,

Без учета начальных условий. Но подобный подход спра­ведлив лишь для таких режимов колебаний, для которых можно допустить, что рассматриваемый момент времепи достаточно удалеп от печального и вследствие рассеива­ния эпсргии, неизбежного в реальной системе, влияние начальных условий достаточпо ослаблено. Этим предпо­ложениям могут соответствовать только режимы нейтраль­ных или близких к ним колебаний. Если же в резуль­тате решения задачи получены значения v = ±oo, то это говорит лишь о том, что необходим учет начальных условий и нелинейных свойств системы. Получив зиаче-

ННЯ V = i od, можпо, по-видимому, утверждать, что в окрестности соответствующих значении Qp и Qv система становится особенно устойчивой или особенно неустойчивой.

Если с учетом этой оговорки построить линии V =• О и v = ± со в плоскости параметров Qp, то будет получена совершенно симметричная картина, изображен­ная на рис. 36. Прямые v = — f со п v = — со идут под 45° к осям координат, поскольку а* = а^., — Ь23. Точно такие же рассуждения можно было бы провести и для диаграмм

Рпс. 37, Изменение величиям v при движеапя вдоль прямых АЛ’ и ВВ’ па рпс. 3G.

А, б п г на рис. 35, получив на них линии v = — f со н v = — со. Этп линии позволяют составить качественно правильную картину изменения v на всей плоскости параметров. Если, например, считать, что Qp остается постоянной величиной, а Q)y изменяется (ли пин А А’ па рпс. 36), то кривая изменения v будет иметь вид, показанный в верхней части рис. 37, а если смещаться по пекотороп прямой ВВ’, то изменение v в зависимости от положення изображающей точки на линии ВВ’ будет иметь вид, показанный в нижней части рис. 37.

Границы устойчивости для общего случая. Для по­строения границы устойчивости в общелі случае целе­сообразно поступать следующим образом. 13 б. в. РаушеиОях

Коэффициенты Сх, С2, С3 и Сл, входящие в систему (23.7), являются линейными функциями Qp и Qv. В самом деле, указанные коэффициенты составляются из линей­ных комбинаций a.,j и которые, как уже указывалось, равны

Ап — «;, + a’nQr, avi = а13 — f «аі = + a22 = агі + nnQp-

Поэтому систему (23.7) можно представить как линей­ную относительно Qv и Qv с коэффициентами, завися­щими от v н со, причем v и со следует рассматривать в качестве параметров системы. Несложные алгебраи­ческие преобразования позволяют написать вместо (23.7) следующую систему:

Wn(v, CO) f (?/12(v,0)) = /’J3(v, 01), <гЛі (v, CO) + <?/32 (V, (rt) = (V, to).

Здесь функции Fik являются суммами вида

A^Cu+Ьг) v cos ^ ш _j_ ^м cos — f — cos k2a> — f д4,

Для первого равенства написанной системы и суммами впда

/jjcC1 і+л8> v sin (Лх — f Л2) со — f 62e»iv sin hx a) — j — b3ch*v sin h2 a>

Для второго равенства (nt, bl —• пекоторые постоянные коэффициенты).

Фиксируя значения V и со, можно, вообще говоря, находить соответствующие им Qp и Q]:

(24.12)

Где

F„(v, to) /-‘,. (V, to)

Лі (V. Ш) (V. ®)

Л» (v. °>) >’ 12 W. <°)

F2S(v, to) Fw{,ts>)

Fn(v, to) F]3(v, to)

‘ } (24.10)

J (24.11)

F21(v, to) (v, ш)

При Д = 0 система подлежит дополпительпому иссле­дованию. Если при этом одновременно оказывается, что Д =0 (или Дв=0), то, как известно, уравнения (24.11) являются линейно зависимыми и их совокупность опре­деляет не точку в плоскости параметров (Qp, Qv), а прямую. Ниже этот случай будет рассмотрен более по­дробно.

Если отвлечься от комбинаций значений (v, со), для которых Д = 0, то каждой точке в плоскости (v, аз) будет соответствовать точка в плоскости параметров (Qpf Qb). Прп движении по произвольной кривой в плоскости (v, to) равепства (24.12) дают возможность находить соответ­ствующую кривую в плоскости параметров (Qit, Qv).

Практически чаще всего приходится рассматривать движеппе в плоскости (v, со) по прямым, параллельным оси со- Ути прямые соответствуют режимам колебаний с постоянными значениями л>. Здесь можпо, в частности, рассмотреть режим с v=vl (vx < 0), т. е. с постоянным декрементом затухания колебаний; режим v = v2 (v2 > 0), т. е. постоянным инкрементом возрастания колебапин, и, накопец, режим v = 0 — границу устойчивости. Послед­ний режим представляет обычпо наибольший интерес. Поскольку во всех этих случаях v — const, то коэф­фициенты FiU системы (24.11) становятся для каждой из соответствующих кривых в плоскости (Qp, Qr) функ­цией только одного параметра — частоты со.

Построив сершо такпх кривых для различных v = const и для всех значений частот 0 < со < со на каждой кривой*), можпо получпть полную и весьма наглядную картину поведения колебательпой системы при любых Q, и Qb.

Построение этих диаграмм является несложной, но достаточно утомительной работой. Принимая во внимание то, что с увеличением со в реальных системах заметно возрастают потери, при расчетах следует ограничиваться некоторой разумной величиной со. Обычно для грубого задания верхней границы со порядок ожидаемых частот можно оценить достаточно точно.

) Из уравнений (23.7) видно, что изменение з па на о» не при­водит к нарушению равенств, следовательно, достаточно рассма­тривать интервал 0 < ш < со вместо — со < ш < со.

Чтобы дать наглядное представление о такого рода диаграммах, рассмотрим пример построения. Приведен­ный ниже пример является достаточно типичным, и в то же время выбраи так, что построение линий v = const оказывается возможным провести без утомительиого вычи­сления координат точек этих кривых.

Пусть плоскость теплоподвода 2 расположена в сече­нии трубы, которое определяется равенством hJ=*hs = k.

Тогда система уравнений (23.7) заметно упрощается и принимает следующий вид:

C1e’-2,iV cos 2/гш + (С, — f C:i) e,,v cos /т C4 = 0, 1 / sill h(0 [2Cje3’lv cos ha -(- eliV (C2 + r;t)J = 0. J

Найдем границу устойчивости. Для этого исследуем систему (24.13) при v = 0.

Рассмотрим сначала особый случай: sin Лаз = 0. Зна­чению sin/ко = 0 соответствуют два возможных значения cos Лео. При cos h(o — I из первого уравнения (24.13) имее. м:

^1 + ^2 + ^8+^4 = 0, (24.14)

Пли, в соответствии с формулами (23.6) «21 •= 0, что дает на основании равенств (24.10) прямую

<24Л5>

Для cos /т = — 1

Г;г-(63+6’3) + С^0. (24.16)

Что после аналогичных преобразований приводит Kr/J2 = U, т. е.

(24-17)

Пусть теперь sin/гіо Тогда, сокращая на этот

Множитель второе равенство (24.13), найдем путем исклю­чения cos/zco пз системы уравнении (24.3 3), следующее условие существования границы устойчивости:

— С, + Гл = 0, (24.18)

Ил II

Вц + вя = 0. (24.19)

Воспользовавшись формулами (24.10), напишем уравне­ние зтоіі прямой и плоскости (Q, Qv)

CCQp + a’Jl — I — a’n ■ J-«4 = 0. (24.20)

Здесь надо заметить, что если прямые (24.15) и (24.17) целиком являются границами устойчивости, то относитель­но полученной прямой (24.20) этого сказать нельзя. По­следнее связано с тем, что cos hto в уравнениях (24.13) не может иметь абсолютпоіі величины, превышающей еди­ницу. Найдем концы отрезка, лежащего на прямой (24.20) и принадлежащего границе устойчивости системы. Второе равенство (24.13) после сокращения па sin /но н исполь­зования (24.18) принимает следующий вид:

(6,1 + Г4)сояЛт + (С8 + Ся) = 0.

При изменении СО ОТ 0 до СО cos Лео будет периодически. меняться от і до —1. В крайних точках cos /ш, равному + 1 или —1. будут соответствовать уравнения

Г1 + 6’4 + 6’2 + 6’3 = 01

Гп + ^-^ + СзНО.

Сравнивая :>тн равенства с формулами (24.14) н (24.1(5), нетрудно видеть, что коицы искомого отрезка лежат на прямых (24.15) И (24.17).

Следовательно, границами устойчивости в рассматри­ваемом случае будут две прямые, параллельные осям коор­динат, к паклоппын отрезок, лежащий между этими пря­мыми.

Построение границ устойчивости бывает полезно до­полнить аналогичным вышеприведенному построением

Линий ПОСТОЯННЫХ V.

Следует лишь учесть, что При V ф 0 во все формулы вме­сто С, войдет а вместо Сг—Ся надо будет писать (С2+С3) ehv. Осуществление этих расчетов совершенно элементарно и здесь излагаться не будет. Легко сообразить, что и в этом случае в рассматриваемом примере линиями постоянных v будут служить прямые линии.

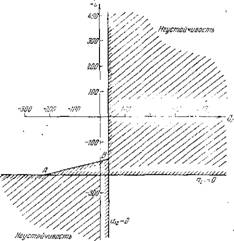
Диаграмма границ устойчивости и линий, равных v для e, iV=l, l (v > 0) и e’tv=ji — (v < 0), построенная по ука­занной здесь методике, дана на рпс. 38. Построение выпол­нено для УІ/j = 0,1, Mt — 0.25.

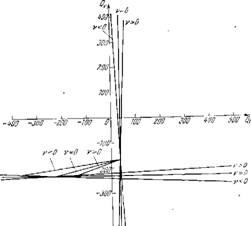
Рис. 38. Линии равных v вблизи границы устойчивости.

Как впдно из приведенной диаграммы, распределение областей устойчивости (v < 0) и неустойчивости (v > 0) напоминает распределение их на рис. 35, ви?. Диа­грамма 38 указывает на одно существенное обстоятельство, которое всегда следует иметь в виду. Линии равных v (на рпс. 38 три группы линий, условно иомечеипые v < 0, Y=0 п v > 0) пересекаются в плоскости параметров колеба­тельной системы ((?р, (?,.). Следовательно, в точке пересе­чения линий v > 0 и Y < 0 система должна быть одновремен-
no и неустойчивой и устойчивой, в точке пересечения лн — иий v = 0 и v > 0 нейтральной и неустойчивой одновремен­но и т. д. Этот вывод пе содержит в себе неразрешимого противоречия, как ;>то может показаться на первый взгляд. Дело в том, что иересекающнмся линиям соответствуют разные частоты, а то, что одна гармоника при заданных () и Qt. может быть более устойчивой, а другая менее устой­чивой, почти очевидно. Пример этого приведен, в частно­сти, па рпс. 38. Если бы вместо рпс. 38 была построена пространствепная диаграмма с частотой to, отложепной по третьей оси, то линии равных v и не пересекались бы, а перекрещивались на разпых высотах (прп разных to). Чтобы дать возможность судпть о том, каким частотам соответствуют точки на линиях равных декрементов, вдоль этих лпний бывает полезным делать разметку частот. На рис. 38 такая разметка не сделана, однако читатель без труда может восполнить этот пробел, если учтет, что пря­мая, идущая вдоль оси Qv, получена для sin /ш = О и cos /*ю — —1; прямая, идущая вдоль оси Qv~ для sin /газ = 0’и cos hсо ^ 1. а группа наклонных прямых — для всех остальпых со.

Ие следует думать, что для отделения областей устой­чивости от областей неустойчивости необходимо, помимо линий v = 0, стропть еще линии v > 0 и v < 0. Такой более ограниченный результат можно получить и проще, восполь­зовавшись так называемым правилом штриховки. Это пра­вило часто используется в теории автоматического регу­лирования, где ппогда носит название метода £)-разбиенпя пространства параметров системы. Хотя этот. метод ис­пользуется в теории регулирования для характеристиче­ского уравнения, имеющего вид полинома, он остается справедливым и для трансцендентных уравнений. Желаю­щим более но л по оз па к омиться с этим методом, полезно обратиться к специальным руководствам Здесь будет дано лишь краткое понятие об этом методе и указаны прак­тические приемы пользования нм.

Математическую основу описываемого ниже правила штриховки можно изложить следующим образом. Уравие-

(24.21

‘) См., например, м. Л. Л й а е р м а н, Лекции по теории автоматического регулирования, Гостехиздат, Москва, 1958 шія (21.11), ко торые будут кратко записаны так:

R(Qiit {),, v, ш) = 0,

!(0):, Q,, v, ш) = 0,

Можно рассматривать и качестве уравнешііі нреооразова- нніі некоторой области в нлоскос-ти (v, со) в область в пло­скости (<?„, (?,„) н обратно. Слева на рис.. 39 дана плоскості, {V, 0)). Каждой точке этой плоскости соответствует вполне

Ш
	У
Л

Я

У;

Рік*. 39. ОтоҐфпясепие плоскости (v, (о) ил плоскость параметров (Q,,. Q,-).

Определенное состояние колебательной системы (точнее, определенная частота п темп возрастания пли убывания колебаний). Справа дана плоскость параметров системы (Q Qt), каждая точка которой определяет некоторый процесс в зопе теплоподвода.

Пусть система (24.21) имеет некоторое решение, на­пример, при Qv — Q?> и Qv — Qv возникают колебания с v=vл и ш=(йл. Первой паре чисел соответствует точка А ‘ на плоскости (Qf], второй паре — точка А на плоско­сти (v, со), Можпо поэтому говорить, что точка А’ соответ­ствует точке А н наоборот. Если непрерывно изменять v и со, двигаясь, например, вдоль кривой АВ па плоскости (v, со), то соответствующая точка в плоскости (Q. (?,) будет тоже смещаться, двигаясь по некоторой кривой А ‘В’. Это позволяет утверждать, что кривая А’В’ является ото­бражением кривой АВ. В курсах математического анализа доказывается теорема, согласпо которой однозначное вы­ражение Q, и Q, как функций от v и со возможно только

При условии, что функциональный определитель д И дН

ДИ dR

DQP dQv IL дІ

DQtJ dQ„

Отличен от нуля. Прп этом оказывается, что знак определи­теля (24.22) играет важную роль. Пусть, помимо кривой АВ, в малой окрестности точки А в плоскости (v, со) дан еще отрезок АС> который лежит справа от кривой АВ, если двигаться от А к В. Отрезку АС в плоскости (Qp, Q}) соот­ветствует отрезок А’С’. Если А > 0, то преобразование (24.21) обладает тем свойством, что отрезок А ‘С’ будет ле­жать тоже справа от А ‘В’ (движение от А’ к В’). Если же А < 0, то преобразование (24.21) изменит положение точки С и она будет ориентирована противоположным С обра­зом: если С лежит справа от А В, то С будет лежать слева от А ‘В’.

(24.22)

Этим свойством преобразования (24.21) можпо восполь­зоваться следующим образом. Выберем в качестве кривой, изображение которой в плоскости (QP, Q,) ищется, ось ордппат в плоскости (v, со). При движении от точки D к точке Е в плоскости {Q h Qt) будет получен отрезок кри­вой D’E’. Пусть, для определенности, для всех рассма­триваемых зпачеппй со Д > 0. Тогда можно провести такое рассуждепие. На линии DE система нейтральна (v=0), следовательно, линия D’E’ является границей устойчиво­сти в плоскости параметров ((7 Qt). Справа от линии DE лежит область v > 0 (неустойчивость). Следовательно, спра­ва от D’E1 будет лежать область параметров Q, при которых колебательная система будет неустойчивой. Если бы было А < 0, то область неустойчивости лежала бы слева от D’E’.

Приведенные здесь соображения позволяют сформули­ровать такое правило штриховки. Будем, положив в урав­нениях (24.21) v=0, изменять со от — со до + со1) и нахо­дить для каждого значения ш соответствующую точку в плоскости параметров (Qp1 QJ. Совокупность этих точек
определит кривую, па которой будет задано направление движения (от точек с малыми со к точкам с большим со). Условимся штриховать правую сторону этой кривой, если А > 0, и левую сторону, еслп А < 0 *). Это приведет, в соот­ветствии со сказанным выше, к тому, что окрестность гра­ницы устойчивости, соответствующая v > 0 (неустойчи­вость), будет заштрихована.

Дальнейшее рассмотрение вопроса о штриховке гра­ниц устойчивости и, в частности, случая А—0, удобнее ве­сти не на основе весьма общих равенств (24.21), а пользуясь записью этих равенств для изучаемого случая (24.11). Существенным прп этом оказывается то, что величины Qp и Qn входят в них лпнейио. Функциональный опреде­литель (24.22) будет в этом случае равен

]/’■,,(<), (о) /^,(0, (о)| А = к(0, <0)^(0. Ш)!’ (24-23) т. е. будет совпадать с определителем линейной (относи­тельно Qp и Ql) системы (24.11). В тех случаях, когда Д = 0 н, кроме того, Ap=0 (пли А,,=0), уравнения системы (24.11) становятся линейно-зависимыми и, как уже указывалось выше, определяют не точки, а прямые в плоскости <?,). Будем называть этп прямые особыми прямыми. Если А = 0 при отличных от нуля А и Ап то это означает, что граница устойчивости в плоскости (Qp, Qx) уходит в бес­конечность.

Поскольку входящие в (24.23) функции Fik являются непрерывными фупкцпямп (0, постольку и А является не­прерывной функцией си, и следовательно, можем изменять знак лишь переходя через нуль. Поэтому штриховка кри­вой. о которой говорилось выше, может изменяться ЛІІНІ1. при встрече ее с особой прямой или нри уходе ее в беско­нечность. Штриховка особых нрямых ведется в согласии со штриховкой кривых.

Проиллюстрируем сказанное здесь на примере диаграм­мы, построенной на рис. 38. Как можно убедиться из фор­мул (24.13), (23.6) и (24.10), особыми прямыми в рассмат-

1) В теории регулирования обычно штрихуют левую сторону upu4>0 и правую прп Д<0. Здесь принято другое правило, посколь­ку в настоящей квигс штрихуется область неустойчивости, риваемом случае являются лишш п а для

Остальных значений о) все точки границы устойчивости ложатся на прямую АВ (рис. 40). Численный расчет пока­зывает, что значепито © — 0 соответствует точка А на рис. 40; по мере увеличения со, изображающая точка движется

Риг. 40, Диаграмма граппц устойчивости, еоотвотсчвутщаи случат, непораженному на рис. 38.

К В и при /го = я приходит в точку В. Здесь определитель Д^ который был прп движении от Л к В положительным, оораіцается в ну. и,, а прп дальпепшем увеличении со ста­новится отрицательным. Изображающая точка движется прп этом от В к А; после достижепия ею точки А она вповь движется к В и т. д, Прп этом всякий раз, когда точка движется от А к В, Д > 0, а при движении от В к А А < 0. Очевидно, нижняя часть отрезка А В должна быть заштри­хована. В точке А особая прямая ап — 0 имеет общую точку с линией А В и в этой точке согласуется штриховка АВ и ап = 0. Это согласованно ясно из чертежа. Особая прямая «12 = 0 штрихуется в согласил с характером штри­ховки линии А В в точке В.

В результате получается картина, показанная па рис. 40. Области, внутрь которых направлена штриховка, соответствуют неустойчивости. Сравнение диаграмм, при­веденні, їх на рис. 38 п 40, показывает пх полное совпа­дение. Таким образом, правило штриховки позволило по­строить диаграмму областей устойчивости без нахождения линий равных зпаченпй v.

Следует сказать, что такая простая конфигурация диа­граммы получилась потому, что было задано нужное для этого положенпе 12 вдоль трубы: В общем случае

Получается значительно более запутанпая картина, хотя само по себе построение п штриховка границ устойчивости ведется столь же просто.

§ 25. Анализ условий возбуждения

В предыдущем параграфе был иодробно рассмотрен воирос о конфигурации областей устойчивости и неустой­чивости в плоскости параметров колебательной системы Qv и Qv. Однако ясио, что умение указать на желательные, пли, напротив того, опасные комбинации величин Q и Qv дает сравнительно мало, еслп не знать, какпм образом эти величины выражаются через привычные для конструктора камеры сгорания (или иного устройства) величины.

Ниже будет дан пример анализа условий возбуждения, основанный на предыдущих результатах, применительно к возбуждению колебаний в спстеме, состоящей из камер сгорания специфического типа и присоединенных к ней входной и выхлопной трубы.

Пусть область сгорания о, которая затем мысленно сво­дится к поверхности разрыва Z. обладает следующими свойствами. Перед зоной а по трубе течет чистый воздух, а внутри областиff расположеныфорсуякп, распиливающие горючее. Горючее мгновенно распределяется по зоне а и мгновенно сгорает. Поскольку давление подачи горю­чего весьма велико, а колебания давления в потоке отно­сительно незначительны, расход горючего через форсунки постоянен п не зависят ни от давления окружающей среды, пи от скорости течения. Эта идеализация должна быть при­знана довольно грубой, хотя бы потому, что в ней пе учи­тывается время, необходимое на смесеобразование, испа­рение горючего, время задержкп воспламенения и т. д. Влияние подобного запаздывания будет изучено ниже. Что же касается принятой схемы процесса внутри о, то ее крайняя простота позволяет проанализировать рассма­триваемый случай до конца.

Поскольку расход горючего никак не зависит от состоя­ния колебательной системы, п поскольку влияние запазды­вания здесь не рассматривается, отличное от нуля возму­щение теплоподвода Q может возникнуть лишь в резуль­тате возмущения полноты сгорания введенного в поток горючего. Опыты говорят о том, что полнота сгорания мало зависит от давлення среды, если это давление незначи­тельно отклоняется от нормального. При горении смеси в открытой трубе давление действительно колеблется срав­нительно слабо (на доли атмосферы), поэтому будем ниже пренебрегать влиянием давлення па полноту сгорания. Скорость течения является более существенным парамет­ром. Нередко увеличение скорости потока после нровыше — ппя ею некоторой величины приводит к заметному сниже­нию полноты сгорания. В пределе, при значительном увеличении скорости течения может иропзойтн так назы­ваемый срыв пламени — полное прекращение горения. Наибольшее влпяппе на полноту сгорания оказывает обычно коэффициент избытка воздуха а (отношение факти­ческого количества воздуха в единице массы смеси к коли­честву воздуха, теоретически необходимому для полного сгорания заключенного в ней горючего). Таким образом, примем, что

Пег — Лег (Ui, «)

И. следовательно.

Переходя к безразмерной системе переменпых (4.8), можпо написать:

Дтіг. г <?Псг

Лег = vі + аа (а = 6а/а, Лег = бЛсг’Лсг)- (25-1)

TW Лег

1То определению а прямо пропорционально массе воздуха, поступающего в зону горения (так как расход горючего неизменен)

A = kQlvv

Где к — некоторая постоянная. Очевидно,

Как уже говорилось выше, холодное течение можно считать изоэитропическим = 0). Тогда р, = Qj (4.9) II формуле ДЛЯ Г|гг можно придать окончательны!! вид

П.-г — I — Па ) Ї’] + U’WV (2j-2′

^Т]0Г ^rjcr

ОМ, да Лм — ‘ Иг» — .

‘ Гиг 1(1 Тієї

Горючее, вводимое непосредственно в зопу горения, даст в уравнениях (15.7) член Q*. Если на единицу площади сечения потока в зону а в единицу вре. мени вводится горючее С химической эиергизп Qumi — которое сгорает СО СрЭдИеп ПОлнОТОІІ СГОрдіІИЯ Лег» ТО х " Л^л^хич’ Поэтому с учетом (15.8) имеем

П* _ 6<3* _ Чсг<?иця — У Єї»! Псг’

Пли, переходя к Q (16.1).

$ = filer, (25.3)

Dp

П ^^хЛсгС/хчм

Сравнивая формулы (24.2), (25.2) и (25.3), можно утвер­ждать, что в рассматривасдюм случае

Qp = Вагь,

Таким образом, величины Qp и (?„ оказались функ — цпямн двух частных производных: полноты сгорания по коэффициенту избытка воздуха а и иолиоты сгорания по числу ЛГ набегающего па зону горения воздушного потока.

Чтобы рассмотреть влияние этих двух частных произ­водных на процесс возбуждения колебании, надо пред­варительно располагать диаграммами устойчивости в плоскости параметров колебательной системы (Qjt, Qn). Такие диаграммы строились в предыдущем параграфе. Здесь достаточно указать, что в большинстве случаев онп имеют вид, аналогичный диаграммам на рис. 36. Такой вид имеет, например, диаграмма устойчивости, построенная для частот, близких к основному тону коле­бательной системы при равенстве длин холодной и нагре­той частей течения. Поэтому воспользуемся указанной здесь диаграммой для дальнейшего анализа процесса возбуждения акустических колебаппй.

Будем анализировать влияние т]а и тц; на колеба­тельную систему раздельно. Пусть сначала г|ГІ = 0. Тогда равенства (25.4) дают

Qp = 0; Q0 = BrM.

На диаграмме рис. 36 этому отвечает движение изображаю­щей точки по оси ординат, причем Qtl оказывается прямо пропорциональным г|д/. Соответствующий график изме­нения v приведен в верхпей части рпс. 37. Как видно из графика (на нем дана шкала Т]м), система становится неустойчивой при некотором отрицательном значении Т. е. при некотором Г|ДІ < 0.

Пусть теперь тім = 0. Тогда по равенствам (25-4)

Отсюда

<?, = %■ (25.5)

Таким образом, при изменении г|а изображающая точка движется в плоскости (Qp, Qy) по прямой (25.5). Этому соответствуют движение но прямой ВВ’ на диаграмме рис. 36 и графяк изменения v в нижней части рис. 37.

Началу координат на диаграмме рис. 36 отвечает r|u — О, положительным v]w— движение в направлении от В к В’. Это приводят к связи между г)а и V, показанной на рис. 37,

М

Рис. 41. Области, в которых наиболее вероятио воз­буждение системы (помечены стрелками).

Из которой можно видеть, что возбуждение системы невоз­можно только при т]а, близких к нулю. При достаточно больших по абсолютному значению га (вне зависимости от знака) колебательпая система может быть возбуждена.

Таким образом, колебательпая система будет возбуж­даться прп достаточно больших по абсолютному значению

ТЦ/ < О» Ла < О И ца > 0.

Если обратиться к зависимости полноты сгорания от Мj и а, то условное протекание соответствующих кривых приведено на рис. 41. Здесь же стрелками указаны обла­сти наиболее вероятного возникновения колебаний: %< 0,гш<0. Как видно из приведенных графиков, наибо­лее вероятно возбуждение колебаний при обогащении смеси до а < 1 п прп сильном обеднении смеси а > 1. Следует сказать, что первая пз названных возможностей является, по-видимому, более существенной. Это связано с тем, что прп обогащепип смеси полнота сгорания падает круче, чем при ее обеднении. Кроме того, в области богатых смесей большее зиачепие имеет и коэффициент В, пропор­циональный поступающей в единицу времени в зону горе­ния энергии сгорающего топлива Q^im-

Полученные здесь качественные результаты в целом удо­влетворительно согласуются с опытными данными. На­сколько можпо судить по ряду опытов, вибрационное горение действительно возникает нри переобогащенпи зо­иы горения и в ряде случаев удается подметить его связь с падением полноты сгорания по мере обогащения смеси.

Влпяние связи между полнотой сгорания и числом М поступающего в зону горения потока на возможность воз­буждения колебаний нетрудно проанализировать таким же образом, как это было с, делано выше. Однако указанный фактор имеет, вероятно, второстепенное значепие, посколь­ку заметное влпянпе скорости течения па полноту сгора­ния проявляется, как правило, на режимах, далеких от эксплуатационных. Кроме того, величина т]м входит в вы­ражение для (} (25.4) с множителем, равным единице,

В то время как ца входит с большим множителем

Проведенный здесь анализ имел целью дать простейший пример доведения задачи до величии, которые являются привычными в теории гореиия ц поэтому позволяют лучше ощутить физическую природу процесса возбуждения, В то же время следует иметь в виду, что рассмотренный пример далеко ие исчерпывает всей проблемы об уело внял возбуждения акустических колебании гореиием.

В заключение настоящего параграфа необходимо сде­лать два замечания. Первое из нях сводится к следующе­му. Выше неоднократно указывалось на ту роль, которую играет обратная связь в изучаемом явлении. Рассмотрен­ный приме}) позволяет указать па весьма важный механизм обратной связи, заключающийся в том, что вызванные ко­леблющимся тепловыделением акустические колебания приводят к колебаниям расхода воздуха в зоне располо­жения форсунок. В связи с этим колеблется коэффициент избытка воздуха, что в свою очередь вызывает колебания полноты сгорапия, т. е. тепловыделения.

Второе замечание относится к вопросу о законности иринятоіг в этом параграфе идеализированной схемы про­цесса и золе горения. Входящие в формулы (25.4) частные 14 Б. в. І’аушсийн* нропзводпые г] tj и i]a, строго говоря, нельзя брать из экспе­риментов, проводимых обычным способом. Дело в том, что когда экспериментатор регистрирует зависимость полноты сгорания от а п М, он проходит ряд стационарных режи­мов с различными фиксированными значениями этих пара­метров. Распространять найденные таким образом законо­мерности (типа представленных на рнс. 41) на сугубо нестационарный процесс — вибрационное горение — мож­но только с известными оговорками и для чисто качествен­ных рассмотрений. По-видимом у, статические характери­стики в общем правильно передают основную тенденцию — ухудшение полноты сгорания по мере удаления от а = Iі).

Если попытаться рассмотреть то новое, что может внести учет иестациопарпостн процесса горенпя, то в пер­вую очередь возникает естественное стремление учесть неизбежное запаздывание процесса воспламенения горю­чего. Это запаздывание обусловлено временем, необходи­мым для испарения н смешения горючего с воздухом, пе­риодом задержки воспламенения и т. д. Учет запаздывания можно осуществить сравнительно просто. Чтобы показать методику этого учета, рассмотрим простой пример.