В заключение настоящей главы верпемся ещё раз к во­просу об источниках энергии, необходимой для возбужде­ния акустических колебаний. В предыдущей главе было показано, что при известных предположениях о характере теплоподвода можпо указать на два принципиально раз­личных источншча энергии акустических колебаний, а в § 18 этот вывод был распространен и на более общий случай произвольного процесса горения смеси, поступаю­щей в зону теплоподвода.

Полученные в настоящей главе формулы, характери­зующие процессы, идущие внутри зоиы горения ст, позво­ляют поставить вопрос о численной оценке относительной •значимости каждого из двух найденных источников энергии.

Однако прежде чем решить, питается ли колебательная система главным образом за счет кинетической энергии течения или за счет энергии, имеющей тепловую форму, необходимо сделать одно замечание. В предыдущей главе были получены формулы (13.7), которые при переходе к без­размерной записи потока акустической эпергии (19.1) примут вид:

Л=407’бії+тб-Ебх)- I

■і / — і і мл> .la = |(46jr + idJ? dx) . I

По этим формулам можно оцепить составляющие пол­ного потока акустической энергии, излучаемой областью а, соответствующие двум независимым источникам энергии. При выводе этих формул использовалось то обстоятельство, что равным долям изменения bp внутри ст соответствовали равные доли изменения bv. Аналитически это условие вы­ражал ос i> фо рм у, із м и (13.3).

В общем случае, при произвольно сложном процессе горения внутри сг, рассуждения, приведшие к формулам (13..»>), окузиваїоїгн неверными. Это следует хотя бы пз того, что формулы (13.3) получены в предположении одно­мерности течения внутри о, в то время как в общем случае это течение может быть существенно не одномерным.

Тем пе менее в настоящем параграфе будут использо­ваться приведенные Здесь формулы ДЛЯ А! п А2. Дело в том, что эти формулы справедливы для всех тех случаев, когдл изменение Ьр и bv вдоль области ст происходит одно­временно и равным долям изменения Ьр соответствуют равпые доли изменения bv. Для одномерного течения в области а это легко доказывается. В общем же случае это является наиболее естественным предположением, так как трудно представить себе реальный процесс

Л*

Горонля, который характеризовался бы, например, тем, что в первой частн области о имеет место только возмущение давления, а во второй — только возмущение скорости, или наоборот. Качественные соображения такого рода позво­ляют использовать полученные рапыпе формулы с выраже­ниями Л j и Л а и для анализа общего случая.

Поскольку в пастоящем параграфе ставится только ограниченная задача оценки соотношения между Л3 и А 2, здесь будет рассмотрен лишь ряд простейших случаев.

При Л=0 (отсутствие потерь на концах трубы) формула (11.9) дает следующее равенство, справедливое для коле­бательной системы, находящейся па границе устойчивости:

Л + 3; = 0, (21.2)

Откуда сразу следует, что А1 = А2. Таким образом, на границе устойчивости абсолютные величины обоих потоков акустической энергии, из которых один обязан своим существованием кыпотическоп эпергип течения, а другой — энергии, имеющей тепловую форму, равны между собой. С этой точки зрения оба источника энергии автоколебаний совершенно равноценны.

Согласпо равенству (21.2) потоки Ах и А.2 имеют раз­ные знаки п на границе устойчивости взаимпо компенси­руются. При этом один из них стремится возбудить систе­му 1 а ДРУг°й гасит колебания. Дальнейшее развитие про­цесса зависит от того, сохранится ли такое равновесие или одержит верх одни из «борющихся» между собой потоков Лг и Л о. Следует при этом иметь в виду, что в зависимости от копкретных условий как возбуждепие, так и гашение колебаний может быть связано с заимствованием энергии нз любого из двух наличных источников энергяи. С этой точки зрения Ах н А» тоже совершенно равноправны.

Условие Л j = — Л2, выполняющееся на границе устой­чивости при отсутствии ноторь во внешпюю среду, инте­ресно в том отношении, что оно дает паглядпое представле­ние о роли двух энергетических резервуаров, которшмирас- полагает колебательная система. Каждый пз этих резервуа­ров может служить источником акустической энергии или, наоборот, поглотителем ее. Если, например, Лг > 0 и, еле-
довательно, А„ < 0, то при колебаниях в зоне горения полу­чается механическая энергия за счет тепловых членов в по­токе энергии, однако эта механическая энергия не расхо­дуется на усиление акустических колебании, а целиком идет на увеличение среднего потока кинетической энергии течеяпя. Если бы система обладала каким-либо одним энер­гетическим резервуаром, то заимствование из него энергии могло бы идти только на возбуждение акустических коле­баний пли па компенсацию потерь во внешнюю среду. Наличие второго энергетического резервуара как бы открывает возможность демпфиро­вания процесса колебаний даже при отсутствии каких-либо внешних потерь.

Чтобы дать количественную оцен­ку энергетических процессов, свой­ственных рассматриваемому явленню в процессе установившихся автоколебаний, обратимся к частному случаю (рис. 31). Рассмотрим закрытую с левого конца трубу. В этом случае поток суммарной акустической энергии влево будет равен нулю, так как излучение аку­стической энергии в окружающее пространство через за­крытый конец невозможно. Но тогда в левой части трубы сдвиг по фазе между pL и у, будет равен ~ и будет спра­ведливо соотпошепие (19.12). Пусть потери акустической э перги її будут всегда равными суммарной акустической энергии А1—А2, движущейся к открытому концу трубы. В этих условиях колебания посят установившийся харак­тер и пользование формулами (21.1) законно.

£

Рдс. 33. Схема тече — ИЛ я акустической энергии в трубе с одним закрытым концом.

/ /

Чтобы получить простую картпну процесса, рассмот­рим тот случай, когда возбуждение происходит за счет колебаний теплоподвода, а подогрев в плоскости 2 слаб (AIl=M„ = М, п = 1 и т = 1). В этих предположениях из формул (20.3) и (17.1) можно пайти

А по формулам (21.1)

(21.3)

1«=т

Где

X —1

А =

2 (J — М2) ‘

Здесь возмущение теплоподвода Q записано в векторной форме. Из формул (21.3) видно, что для рассматриваемого типа колебательного процесса вторые слагаемые в Лх н Л3 всегда дают отрицательные составляющие, т. е. всегда гасят колебания. Следовательно, возбуждение системы можно производить только за счет первых слагаемых, причем в ЛА %> и Q должны для этого составлять угол, пе превышающий ~ , а в Л2 н Q должны составлять

Угол больше — у ■ Поскольку pt и ь в левой части трубы, примыкающей к закрытому концу, связаны условием (19.12)

Г} + р = const,

То возможные наибольшие абсолютные значения рх и совпадают. Сравнение первых слагаемых выражений (21.3) показывает, что величина потока акустической энергии, идущей на возбуждение системы за счет кинетической энергии течения, возрастает прямо пропорционально числу М. При М —> 1 оба источника энергии (тепловой н механический) в этом смысле выравниваются.

Это не значит, что нри малых (по конечпых) М можно просто пренебрегать потоком энергии Л2. Проще всего это можпо впдоть из следующего рассуждения. Пусть первое слагаемое Л2 равно нулю (например, из-за фазо­вого сдвига между Q и?’]). Тогда возбуждепие будет происходить за счет одного только первого слагаемого Av Начнем увеличивать абсолютную величину Q. При этом вторые слагаемые, в которые Q входит в квадрате, будут расти быстрее, чем первое, П нри некотором Q = Qm ах суммарный поток Ах -f Л2 обратится в нуль. Следовательно, возбуждающее действие первого слагаемого Ах будет целиком погашено вторыми слагаемыми Аг и Л2, причем л совершенно одинаковой мере.

Эти качественные выводы хорошо подтверждаются точ­ными расчетами частных случаев тех или иных течений.

Энергии при изменении модуля Q.

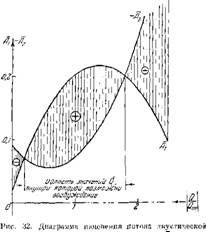
Для иллюстрации сказанного на рпс. 32 ириведепа диаграмма, показывающая, как изменяется ноток акусти­ческой энергии А1—Лг при изменении модуля Q для частного случая 0,1, ЛГа = 0,25, = Как

Видно из нриведеіших чисел, речь идет о сравнительно медленном течеиии: условие взято для того,

Чтобы перед плоскостью теплоподвода иметь заметные колебания как скорости, так и давления. При расчетах фаза Q выбиралась постоянной ц такой, чтобы для задан­ных рх и при некотором модуле Q = (/max обязательно достигался максимум Al-Jr Л2 (вектор Q проходит через центр окружности, являющейся граппцей устойчивости при избранных и 1^). При построении диаграммы по оси ординат были отложены величины Ах и — As, следовательно, расстояние между обеими кривыми по вер­тикали равно потоку Ах-~ А2, нри этом в тех участках, где кривая -/lj лежит выше — Л2, суммарный поток поло­жителен, а там, где —А2 проходит выше AL, — отрицателен.

Из диаграммы видно, что при Q = 0 + О, т. е. нрн отсутствии колебания теплонодвода система устойчива. Выше это обстоятельство уже подчеркивалось при построении границ устойчивости (§ 20).

Приведенная на рис. 32 диаграмма полностью подтвер­ждает полученные в настоящем параграфе результаты. Кроме того, из нее видно, что прп таком сравнительно мед­ленном течении колебательная система возбуждается за счет теплонодвода и потока внутренней энергии, а взаимо­действие системы с потоком кинетической энергии ведет к сильному демпфированию колебаний.

Этот результат вообще характерен для медленных те­чений (Af<l), возбуждаемых теплоподводом. Такцо тече­ния возбуждаются за счет потока кинетической энергии лишь в исключительных случаях, при рг, близких к нулю, причем абсолютная величина А Х + А2 в этих случаях не­велика.

Из сказанного не следует, однако, долать вывода, что поток А з никогда не играет заметной роли как активный фактор возбуждения колебании. Во-первых, с ростом: М доля А2 в общем потоке акустической эпергии пропорцио­нально возрастает, во-вторых, картпна может резко изме­ниться, если процесс в зоне теплонодвода перестанет рас­сматриваться как функция одного комплексного парамет­ра (в рассмотренном случае Q). Если учесть, например, что в зоне теплоподвода могут одновременно происходить и колебания теплонодвода и колебания положения фронта пламени, причем фазовый сдвиг между ними может быть произвольным, то нетрудно построить примеры систем, в которых главным источником энергии для возбуждения колебаний будет кинетическая энергия течения.

Кроме того, если вернуться к рис. 28, иа котором даны границы устойчивости для случаев Vj —0 и рх=0, и учесть, что эти границы построены с соблюдением масштаба для рассматривавшегося в настоящем параграфе медленпого течения, то нетрудно убедиться В том, что А2 может яв­ляться активным фактором возбуждения и в таких исклю­чительно неблагоприятных для этого условиях, как М1 = 0,1. Действительно, диаметр области неустойчивости в правой части рисунка (соответствующей р} = 0) лишь в 2,5 раза меньше диаметра области неустойчивости, изо­браженной слева. В то же время из примера (21.3) видно, что при Ръ = 0 единственным возбуждающим систему по­током акустической энергии является А2, а ири и, = 0 эту роль исполняет Av Следовательно, пренебрежение таким резервуаром энергии для поддержания автоколе­баний, как кинетическая энергия течеппя, может не толь­ко исказить картину в тех случаях, когда возбуждение происходит за счет энергии, находящейся в тепловой форме, но и привести к неправильным выводам о возмож­ности самовозбуждения системы в таких областях плоско­сти параметров, для которых возбуждение колебаний за счет энергии, находящейся в тепловой форме, вообще не­возможно.