Приведенные в предыдущем параграфе соображении указывают на то. что для описания колебапий газовых столбов, лежащих слева и справа от зоны горенпя, можпо по-прежпему пользоваться линейными уравнениями § 4, в то время как для зоиы горения о следует учитывать существенные нелинейности. Первое из этих утверждений хорошо подтверждается экспериментом: эпюры стоячих волн давления, подсчитанные по линейной теории, хорошо согласуются с экспериментальными, снятыми при авто­колебаниях (рис. 53). Справедливость второго утвержде­ния будет показана нпже.

Будем считать, что процесс теплоподвода в зоне горе­ния зависит от колебаний газового потока. Пусть эта зависимость проявляется двояким образом: фронт пла­мени будет подвижным и, кроме того, количество выде­ляющегося на единицу массы газа тепла не будет постоян­ным, т. е. примем, что 0. Отпосптельно подвижности фронта пламени будем предполагать следующее. Пусть эффективная скорость распространения пламени отпосп­тельно степок трубы N, определяемая формулой (16.5), совпадает с мгновенным зпачеппем колебательной со­ставляющей скорости bvv Физически это означает, что колеблющийся поток будет «таскать» за собою фронт пла­мени. Такое предположение позволяет легко найти вхо­дящие в описывающую свойства поверхности 2 (область о) систему (15.7) величипы /1? /3 и Js при помощп соотно­шений (16.2), (16.3) и (16.4). Величину т]сгЧ — <7,, фигури­рующую в последнем равенстве системы (15.7), найдем несколько позже.

Здесь следует заметить, что использование системы (15.7), строго говоря, допустимо лишь для задачи, опи­сываемой лппейиымп соотношениями. Сохраняя предпо­ложение о возможности описания линейными уравнениями процессов на концах трубы п внутри нее, вне области теп­лоподвода а, допустим также, что внутри области тепло­подвода все величипы будут продолжать связываться ли­нейными соотношениями, за исключением члена ‘Псг — h fo, т. е. за исключением возмущения самого теплоподвода. Как будет видно из дальнейшего, последнее ограничение не является принципиальным п его легко спять. Здесь эта возможность не используется для того, чтобы пе делать решения задачи более громоздким.

Используем систему (15.7), соотношения (16.2), (16.3), (16.4) и (16.5), а также учтем, что на основании кине­матического условия (16.6)

6v1 + ЬЬ = bv2 + ьий = 6 N.

Тогда, основываясь на сделанном в начале настоящего параграфа предположении, что бу^бД’ (значение N в стационарном режиме течения, очевидно, должно равнять­ся нулю), и переходя к размерным переменным, придадим системе (15.7) следующий вид:

Q2 bvi — f Vi ^qi = qa — j- c2 6q2, v 6qj + 2Qjt/j 6oj Ц • bpl = v 6q2 — j — 2q2v2 bv2 -1- 6/?2,

— f bQ* ~ ( 4 QA + ~Л ft) ftt’a "г ^T Sft.

(40.1)

Напомним, что — скрытая химическая энергия еди­ницы массы горючей смеси. Отсутствие члена </., указы­вает, что в стацпопариом процессе предполагается пол­ное сгорание (rjcr—1). Из сравнения равенств (40.4), (15.2), (15.4) и (15.7) нетрудно видеть, что

Б7 = Л«г). (40.2)

Т. е. учитывается изменение теплоподвода как за счет изменения скрытой химической энергии единицы массы горючей смеси, так и за счет пзменепия полноты сгорания. В линейной задаче следовало бы написать 6<7 = r}cr6^1-f + (7іАПсг, однако, в предположении, что наиболее суще­ственная нелинейность связана с 617, здесь введена более общая запись.

Будем искать вид нелинейной функции 6q. С этой целью следует прежде всего уточнить характер рассма­триваемого физического процесса. Выберем некоторую идеализированную схему, наиболее легко осуществляе­мую в лабораторпых условиях. Область теплоподвода о упомянутых выше лабораторных установок характери­зуется двумя особенностями: стабилизирующие процесс горения плохо обтекаемые тела невелики по размерам, расположены достаточно густо и все лежат в одном сече­нии. так что длина области интеисивиого горения за ста­билизаторами может быть принята малой по сравнению с длиной горячей частп трубы (протяженность зоны обрат­ных токов за стабилизаторами, грубо говоря, пропорцио­нальна их диаметру); второй особенностью является то, что форсунки, подающпе горючее, расположены в непо­средственной близости от стабилизаторов (£ф на рис. 67 близко к нулю).

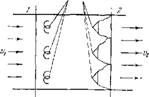
Представим эти особенности схемой, показанной па рис. 77. Пусть сеченпя 1 и 2 дают границы зоны подго­товки смеси и горения, причем расстояппе между ними i

А 6

I

Рис. П. Схегаа зоны горения, принятая в расчете.

Мало. Предположим, что все впрыснутое форсупками «топ­ливо мгновепио распространяется по всему объему менаду сечениями 1 и 2 п сгорает в сечении 2 за стабилизатора­ми б. В дальнейшем необходимое для этого время будет учтено введением времени запаздывания. Еслп считать, что горючее подается форсунками с постоянным расходом const, независимо от колебаний газовой среды, то изменение содержания массы горючего в объеме обла­сти о V=IF (где F — сечение потока) будет равно:

1

JGr dt — QrvFdt,

Где Qr — средняя плотность горючего в объеме IF, а V — скорость потока.

Поделпв полученное выражение на IF, найдем изме­нение плотности горючего в объеме IF: 1 .

-jGp — QrvF

DQr = і ^ dt. (40.3)

Это уравнение опиеыиает изменение плотности горю­чого п в сечеппн 2, в котором происходит горение.

Для того чтобы проинтегрировать уравнение (40.3), следует задать v=v(t). Будем рассматривать установив­шиеся колебания, т. е. положим

V = vQ 4- Av sin со/. (40.4)

После подстановки выражения (40.4) в уравнение (40.3) оно приобретает вид

^ = Л — Bqv — sin соl. (40.5)

Решение уравнения (40.5) не может быть представлено в элементарных функциях. На рпс. 78 сплошными ли­ниями дано численное решение этой задачи прп условии, что в момент 2 = 0 Qr=0. Представленный пример взят для параметров теченпя в топ лабораторной установко, на которой проводились эксперименты для сравнения теоретических расчетов с опытными данными. В расчете было принято, что fo=50 м/сек, Л„ = 50 місек, £=0,2 м, а расход горючего Gv таков, что при отсутствии колеба­ний (Л„ = 0) он дает q,.=0,008 (это приблизительно соответ­ствует коэффициенту избытка воздуха а = 1). Здесь сле­дует пояснить, почому амплитуда колебаний скорости A v взята в рассматриваемом примере равной средней ско­рости течения i?0. Дело в том, что в этом случае наиболее ярко проявляются особенности, которые приводят к воз­никновению нелинейных зависимостей между колеба­нием скорости и тепловыделения. Действительно, как видно из рпс. 78, в рассматриваемом случае для Q=32 гц Ор колеблется от 0,004 до 0,0225, что соответствует колеоанпю коэффициента избытка воздуха от а=2 до а=0,35. Для Q = 16 гц этот диапазон еще шире. Совер­шенно ясно, что при таком колебании состава горючей смеси полнота сгорания будет изменяться сильнейшим образом и безусловно не линейно. Более подробно этот вопрос будет рассмотрен ншке.

Из рис. 78 нетрудно видеть, что процесс колебаний Qr устанавливается очень быстро, а кривая Qr =Qr (/) после

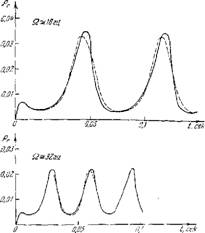
Рис. 78. Расчетное изменение количества горючего в зопо горения при колебании расхода ‘воздуха в плоскости рас­положении топливных ^форсунок.

Установлення колебаний весьма близка по форме к сумме двух синусоид с отношением частот, равным 2. Поэтому будем искать приближенное решение уравнения (40.5) следующим образом.

Предположим, что приближенная зависимость Qr = = Qr(t) может быть записана в виде

Єг = Ого — г D sin (соt + ф) 4- Е sin (2o>J + а). (40.6)

Подстановка этого равенства в уравнение (40.5) по­зволяет найтн входящие в (40.6) постоянные:

P = arctg^-, y = arctg^, С

Sin

‘ 4 /ш’+В’ Vйш’+В’ ф = arctg — сг

■ sm а — cos :

41 y’fo’+B®

A CD

А В

Уа’^В* С С д cos (ФЧ-Р) — 4 (f l-«)-2Bcos4

Е = — CD

2 y ia’+B1

(40.7)

Чтобы проиллюстрировать точность паіідепного при­ближенного решения, на рпс. 78 приведены пунктиром кривые, вычисленные по формулам (40.6) п (40.7). По­скольку совпадение с точным решением получается вполне удовлетворительным (это подтверждается и дру­гими расчетами), в дальнейшем используется приближен­ная методика.

Функции Qr = Qr(Ј) были получены для различных частот Q н для различных амплитуд колебательной со­ставляющей скорости Av. На рис. 79 даны в качестве примера такие кривые для Q = 48 гц и для различных значении Л0. Аналогичные зависимости были построены также для Q = 16, 32, 100 гц (этот диапазон охватывает частоты, которые наблюдались на опытной установке).

В отличие от предыдущего примера, здесь и ниже пред­полагалось, что в отсутствии колебаний камера сгорания работает на а ^1,5. На основании кривых Qr = gr(f, Q, Л(.) строились кривые тепловыделения в функции времени. Для. этого был использован условный график зависимости полноты сгорания от коэффициента избытка воздуха 23 в. В.’Раугпонбах (рис. 80). Функция Г)сг = tier(о&) (сознательно упрощен­ная) выражаот главные свойста такой зависимости: в не­котором диапазоне а (здесь 1<а<2) полнота сгоранпя практически постоянна и близка к единице. Слепа и спра­ва от этой области полпота сгорания резко надает, ста­новясь равной нулю при сильно обогащенной н сильно

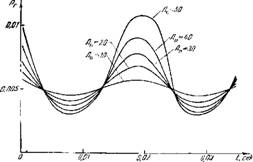
Рис. 79. Изменение количества горючего в зоне горения при разных амплитудах колебаний скорости в плоскости расположе­ния топливных форсунок.

Обедненной смеси (в рассматриваемом случае прп а=0,4 на=4). Нужно заметить, что уточнение этой зависимости не имело смысла. С одной стороны, это лшнь незначи­тельно изменило бы количественные, но не качественные результаты расчета, а, с другой стороны, уточненная по результатам опытов, поставленных на стационарных ре­жимах, зависимость лишь с большой натяжкой могла бы использоваться в расчетах нестационарного (колеблю­щегося) горепия.

Величины Qr и а, очевидно, обратно пропорциональ­ны друг другу, еслп пе учитывать колебаний плотности воздуха, связанных с колебаниями давления. Поскольку относительное колебание давления много меньше относи — г id І существенные нелинейности в зоне горешія 355

Тельного колебания скорости, эта зависимость не учиты­валась. Поэтому связь между Qr на была принята следую — 0 0078

Щей: а = — . Пользуясь этой связью между Qr и а

Qr

И графиком г)сг — "Пег(а), строились кривые Qr’ксг = /(/). Такие кривые выражают в некотором масштабе зависи­мость тепловыделения от времени. Эти графические зави­симости разлагались далее в ряд Фурье, причем для

G 1,0 2,0 3,0 ‘ 4,0 а

Рис. 80. Принятая в расчета зависимость мгповенион пол­ноты сгорапия от коэффициента избытка воздуха а.

Каждой кривой выделялась первая гармоника ряда, соот­ветствующая частоте колебаний скорости оз. Выделение этой гармоники физически оправдано — акустические ко­лебания с частотой оз будут поддерживаться колебаниями тепловыделения, происходящими с той же частотой.

В результате подобного расчета получалась амплитуда искомой гармоники ряда Фурье Лг и фазовый сдвиг ее относительно колебания скорости ср-,:

6q = const Л1 sin (a>t + фх) (40.8)

(химическая энергия единицы массы горючей смеси пред­полагается неизменной; она характеризуется введенной здесь размерной постоянной). Здесь

=-Ij (Л(.; м), ср, = qjj ; со).

Расчеты, проделанные для указанных выше частот и для Av = 10; 20, 30, 40, 50, 60 м/сек, показали, что зна­чение cpj колеблется около я, лишь незначительно откло­няясь от этой величины. Поэтому оказалось возможным

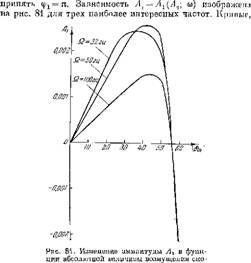
Рости перед зоной горения.

Вычисленные для других частот, идут аналогично. Наибо­лее важными свойствами, общими всем кривым, являются следующие: кривые идут пз начала координат, достигают максимума и вновь пересекают ось абсцисс где-то между |6Уд|г=Д, = 50 м/сек и |6у,| = Д, = 60 м/сек. Для облег­чения дальнейших вычислений было решено пренебречь зависимостью Ах от частоты. Такое пренебрежение не яв­ляется слишком грубым — оно может привести только к незначительному количественному изменению резуль­татов, отнюдь не меняя их по существу. Форма кривой А^ = А1(А,) была приближенно представлена квадратич­ной параболой:

Ах= 0,00000293 (56 — Av) Av. (40.9)

Прежде чем переходить к дальнейшему изложению хода решения задачи, следует указать на причину, по которой в рассмотренном примере все кривые Ax-=Ax(At) вторично пересекают ось абсцисс при 50 м/сек < А0 < < 60 м/сек. Для малых частот этот эффект естествен — прп достаточно больших периодически происходит сильное переобогащение и нереобеднепие смеси, что отри­цательно сказывается па процессе горения. Для высоких частот такие процессы переобогащения и переобеднения не успевают развиться, зато продолжает действовать дру­гой процесс, связанный с нарушением горения при Av > vQ. Когда колебательная составляющая скорости Ібі^^Д, становится больше средней скорости течения vQy ноток начинает двигаться в обратном направлении, а процесс горения на стабилизаторах (расположенных около сече­ния 2) прекращается, поскольку прекращается доступ к ним свежен смеси (продолжающееся на свободной по­верхностп раздела холодных п горячих газов горение играет сравнительно небольшую роль). Это состояние длится не только в течение времени движения продуктов сгорания в отрицательном направлении оси х, по и тогда, когда возобновляется течение в положительном направле­нии, до тех пор, пока в зону стабилизаторов пе начнет поступать свежая смесь. После этого в течеппе некоторого времени горение идет очень плохо, поскольку свежая смесь оказывается сильно переобогащенной — ведь она трижды пересекала область расположения форсунок (прямое пе­ресечение, затем возвращение смеси при течении газов в отрицательном направлении и, наконец, вновь пересе­чение при движении в положительном направлении). Эти обстоятельства сказались прп построении кривых РгПсг=/(0, на осповапни которых находились значения Лг Именно этп явления, связанные с забросом пламенп в область перед стабилизаторами, приводят к резкому уменьшению Ах при Av > vQ.