Одним из первых тщательпо поставленных опытов по вибрационному горению был эксперимент Коварда, Хартвелла и Джорджсона, который уже упоминался в предыдущих главах. Напомним, что в указанном экспе­рименте изучалось распространение фропта пламени вдоль трубы, заполненной неподвижной горючей смесью, причем один из концов трубы был закрыт, а поджигание велось от открытого конца.

В этом опыте почти однозначно определен основной механизм обратпой связи, что допускает достаточно пол­ное аналитическое рассмотрение вопроса. Действительно, поскольку речь идет о горенпи в заранее подготовленной гомогенной горючей смеси, то все механизмы обратпой связи, основанные на смесеобразовании, сразу исклю­чаются. Точно так же исключаются механизмы, в кото­рых основную роль играет вихреобразование и т. п. гидромеханические причины. Из явлений, связанных с собственно горением, сразу исключается вся группа процессов, реализация которых требует наличия под­жигающего источника (ироде ацетилеповой горелки и т. и,). Зависимость скорости распространения пламспи от параметров неподвижной среды, в которую движется фронт пламени, более плп менее известна. Однако ни коле­бания давления, пи колебания температуры в неподвиж­ном газе, которые па б л ю дались в опыте, не могут вызвать столь сильного изменения скорости распространения пла­мени, чтобы система возбудилась. По отой же причине привлечение разного рода соображений, связанных с изме­нением периода индукции, обусловленным, па пример, колебаниями давления, тоже не может дать сколько — нибудь убедительных результатов. По-видимому, главным механизмом обратной связи, который играет в этом опыте решающую роль, является механизм, связанный с перио­дическим волнообразованием на поверхности нламепи, который рассматривался во второй половине § 38.

В отличие от приведенного выше принципиального рассмотрения указанной задачи, здесь будет дано реше­ние для несколько упрощенных условий, но доведенное до конца.

Как уже указывалось в § 3S, прп акустических коле­баниях среды расположенный в ней фронт пламепи испы­тывает действие ускорений, изменяющихся периодиче­ски. В этом случае отклонение возмутцеиного фронта пламени от его стационарного положення х = 0 в направлении оси х (прп некотором заданном значений координаты?/) описывается уравнением Матье (38.25) (здесь z —величина, пропорциональная времени t);

Л" (г) — 2q cos 2zA (z) = 0. (4<J.1)

Поскольку трубы, в которых ставились опыты Ковар — дом, Хартвеллом и Джорджсоном, располагались гори­зонтально, коэффициент а в уравнении (38.25) принят равпым нулю. С тем, чтобы сделать возможным решепие написанного уравнения в элементарных функциях, введем следующее упрощение. Заметім периодическую функцию cos 2z прпблпжеппой, составленной из участков с постоян­ными значениями функцпп, как показано па рнс. 100. Кроме того, сместим начали отсчета аргумента z на у, введя перемениую + Тогда вместо уравнения

(49.1) можно будет паипсать

Л" (г,)+Ф (2,)-4(2,) = 0, (49.2)

Где ф (z,) = + mz для интервалов 0 < z, < , я < z, < ^

И т. д. н ф (z1) = — т — для интервалов < г, < л,

Дт — < Н < 2л и т. д.

Величина т- определяется при это. м следующей фор­мулой:

Приведенное здесь выражение для т2 нолучепо из сравпения уравнения (38.25) с уравнением (49.2).

Л

		Ж V			Іл г

‘л

Рис. 100. Замена косинусоиды разрывной функцией тона меандра.

При этом учтено, что средпее значение cos2z на интер­вале, где эта функция не меняет знака, равно по абсо­лютной величине 2/я.

Уравнение (49.2), так же как и уравнение Матье, является уравнением с периодическим коэффициентом (коэффициент при /1 (zx) изменяется в функции г, по закону, изображенному па графике в нижней части рнс. 100). В соответствующих разделах математического анализа показано, что уравнение такого типа имеет решение вида

,1 (z,) = С/Л/і U,) + C>Vi/2 (Zj), (40.4)

К которому принадлежит и решеппе (38.26). Прп этом функции fl(z j) п /а(22) янляются периодическими, а характеристические показатели Sj и. s2 —постояпиыми величинами.

Будем, основываясь на сказанном, искать решение уравнения (49.2) в виде

А(г,) = Се’^Ы- (49.5)

Разобьем всю ось Zj па участки длиною — ; уча­стками первого типа будем называть те, в которых ф (z:) = m2, участками второго типа те, где <р (лх) = — т2. Рассмотрим совокупность двух соседних участков пер­вого и второго типа. Пусть, для определенности, это будут участки 0<z2<-^ и Тогда решением

Дифференциального уравнения (49.2) будет для первого участка

Л1 = сут:’ + С>~4′,,г1 (49.6)

И для второго участка

Л2 = 6’3e"lzi + С4е~тгк (49.7)

Эти решения необходимо «склеить» должным образом. Для этого надо потребовать, чтобы на соприкасающихся границах участков величины Л, и Л2, а также производ­ил. dA2 rp пыс —fa н ~fa^ совпадали. Кроме того, следует учесть

Требование, которое является следствием периодичности фуякцнп /(г,) в равенстве (49.5). Обозначим период рас­сматриваемой функции через т; тогда естеетвеппо допу­стить, что этот период будет совпадать с периодом функ­ции ф(гх), входящей в уравнение (49.2), илп будет кра­тен ему. Перпод функции ф (z:) равен, как это следует из рис. 100, т = я; поэтому можно написать еще два
условия, связывающие начало и конец интервала, соот­ветствующего совокупности двух соседних участков пер­вого и второго типов: aAj (0) = Л2 (л); a (0) = (я), где Ъ = ечЯ. Таким образо. м, имеем следующие четыре условия:

У 2 у У г — (49.8)

<1Л, f я Л йЛи / я Л ‘/. I, ‘/. г, ,

Подстановка в условия (49.8) решений (49.fi) и (49.7) дает следующую систему уравнений:

TOC o "1-3" h z • 5 _ • — .

(49.9)

С, е"" 2 + С2с 2 — С3е" 2 + 2 = О,

, л, л л л

• si 1гп ~ї -«л — т ^ —?«-

Схе г — IC2p. ‘- — С3е L + С4е z = О,

A Сг + a С8 — Сьгтп — C. le~nm = 0, iaCj — taC2 — С>тя — fC4e-HtIt =0.

Система (49.9) может иметь петривиалыше решения только в том случае, если ее определитель равен нулю. Если написать это условие, го после несложных, но достаточно громоздких вычислений получим следующее равенство:

A + L = 0

А2 — 2 cos т ~ ch т a — f 1 = 0. (49.10)

Пользуясь написанным здесь равенством, можно найти два значения ее, при которых система (49.9) имеет реше­ния, отличные от нуля. Эти два значения (сц п а2) опре­делят два значения характеристических показателей Si и s2, входящих в общее решение (49.4). Даже не находя числепных значений и а2. можно указать на некоторые свойства этих величин. Из вида коэф­фициентов квадратного уравнения (49.10) следует, что
ига2 = 1. Следовательно, если модуль одного из чнсел больше единицы, то модуль другого меньше единицы, и наоборот. Таким образом, отлпчне модуля одного из чисел или а2 от единицы говорит о том, что волновое движение на поверхности пламени неустойчиво, так как тогда средп cij и а2 обязательно существует |а|>1, что соответствует s > 0, т. е. неустойчивости [не следует забывать, что независимая переменная в решении (49.4) пропорциональна времени t. Следовательно, устой­чив ый процесс (без нарастания амплптуд колебаний со временем) возможен только при а1 = а2 = 1 илн прн комплексных значениях и а2. Действительно,

Я, л, . . /, „ л, „ л alt 2 = cos т — cb т — j ± і у I — cos — т — clr т.

При cosm^zhm~<, 1 модуль числа или а2 (квадрат которого равен сумме квадратов вещественной п мнимой частей) в точности равеп единице. Это говорит о том, что характеристический показатель s имеет вещественную часть, равную нулю, т. с. амплитуды волн на поверх­ности нламени не станут возрастать с течением вре­мени zv

Формула (49.11) показывает, что величипы a1( 2 зави­сят от числа т. Проанализируем это влияние числа га па устойчивость более подробно. Такой анализ будет аналогичен рассмотренному в § 38 вопросу о влиянии коэффициента q на характер решения уравнения Матье. Сравнивая уравнения (49.1) и (49.2), .можно установить между этими двумя параметрами численное соответствие, приближенно отвечающее существу явлении:

(здесь принято, что средпее абсолютное значение cos 2z 2

Равно —).

Л’

При непрерывном изменении числа т корни at и «2 будут также меняться непрерывно. В силу того, что а1а2= 1, достаточно следпть за каким-либо одним из этих корней. Прежде чем приступать к анализу зависимости а от т, напомним, что функция eh?; является четной, всегда положительной, монотонно-возрастающей по | х и достигающей наименьшего значения ch:r = 1 при я = 0.

Пусть т увеличивается ог 0 до со. При т = 0 а1 = 1. При увеличении т ах становится комплексной величиной, пока cos2 т-у ch2 т не начиет ^вследствие монотон­ного возрастания превышать единицу. В этот момент a j станет вещественным корнем. Далее, вслед­ствие приближения cos2m-^ к нулю сц вновь примет комплексное значеппе и т. д. Следовательно, а1 будет периодически становиться то вещественной, то комплекс­ной величиной, причем по мере роста т интервалы зна­чений т, где at — комплексная величина, будут делаться все более узкими вследствие быстрого роста ch2m-^-.

Описанному здесь чередованию интервалов значений т, где корень dj является вещественным или комплексным, соответствует чередование областей устойчивости и не­устойчивости волнообразования на фронте пламени. Такое же чередование областей устойчивости и неустой­чивости описывалось и выше, прн рассмотрении уравне­ния Матьо (см. § 38).

Численный анализ дает в рассматриваемом случае следующие результаты:

При 0 < т2 < ‘1,39 at — комплексная величина,

При 1,39 < tn’2 < 9 cij — отрицательная вещественная величина,

Прп 9 < т2 < 25 а, — положительная вещественная ве. личин а,

Прн 25 < тг < 49 (ij — отрицательная вещественная величина,

При написании этих неравопств не принимались во внимание узкие интервалы значений т1 около т2 = 9, т — — 25, ?пг — 49 …, в которых ctj является комплексной во дичиной (непрерывный переход от cij отрицательных к ctj положительным и обратно происходит через ком­плексные значения а2).

Если сопоставить эти интервалы с соответствующими интервалами значений коэффициента q в уравнении Матье (см. § 38), то, пользуясь формулой (49.12), можно соста­вить следующую сравнительную таблицу значений q:

Интервалы зпачешш соответствующих областям неустойчивости

По уравнению Матье (19.0	170 ураиненшо (49.2)
0.91<?<7,5 7,5<?<21 21<5<42	1,09<?<7,05 7,О5<?<19,0 1Э,6<?<38,4

Как видно из приведенной таблицы, численное соот­ветствие между обеими сериями областей получилось много лучше, чем можно было бы ожидать от столь грубой идеалпзацни — замены синусоиды ступенчатой разрывной функцией типа меандра. Это обстоятельство позволяет надеяться, что н другие стороны изучаемого явления будут переданы приближенным уравнением (49.2) не только качественно правильно, по и со вполне удовле­творительным количественным соответствием.

Как известно из § 38, где рассмотрено уравнение Матье, в иервом и третьем интервалах, помещенных в таблице, период функций / (га) в решении (49.4), част­ным случаем которого является и решенпс (38.26), равен 2я, в то время как во втором интервале он вдвое меньше. Тем же свойством обладают и функции /(zA), полученные путем решения уравнепия (49.2). Действи­тельно, для первого и третьего интервалов сц является отрицательной величиной, а для второго положительной. Следовательно, в последнем случае функция / (z,) вер­нется к той же фазе (точнее, фаза изменится па 2я) при изменении гл на я, а в первом случае (ал < 0) фаза } {zx) будет отличаться от исходной на я (так как амплитуда /(z,)
изменит свой зиак). Поэтому прн щ < 0 возвращение к начальной фазе потребует двух шагов, каждый из которых сменит фазу иа я, а оба вместе на 2л. Этим п доказывается высказанное утверждение.

Выше, в конце § 38, уже говорилось, что для того, чтобы колебания поверхности фронта пламени могли играть роль механизма обратной связи, поддерживающего акустические колебания среды, период этого волнообра­зования должен быть вдвое больше периода акустиче­ских колебании (в переменной zx равного я). Поэтому для анализа взаимодействия волнообразования на поверх­ности пламени и акустических колебаний следует рас­сматривать только те диапазоны значений иг2, для кото­рых является отрицательной вещественной величиной. При этом наибольший интерес представляет первый из этих интервалов 1,39 < т — < 9, который соответствует [как это следует нз формулы (49.3)] наименьшим ампли­тудам смещений среды при акустических колеба­ниях /г0.

(4У.13)

Чтобы получить наглядное представление о функции Л(2і), являющейся решением уравнения (49.2), приведем здесь численный пример. Пусть первоначальное возмуще­ние на поверхности пламени было достаточно малым и к рассматриваемому моменту прошел достаточно боль­шой промежуток времени, чтобы одно из слагаемых решения (49.4) уменьшилось до пренебрежимо малой величины. Поскольку здесь рассматривается случай не­устойчивости, | ctj | > 1, то в силу условия аха, г = 1 | а21 < 1, т. е. второе слагаемое будет уменьшаться с течением времени. Выберем значение т2 вблизи от границы пер­вого интервала, характеризуемого а4 < 0. Пусть, напри­мер, ?пг = 1,46. Тогда о, = —1,6. Выберем за начало отсчета времени zx момент, когда величина A (z2) веще­ственна и равна единице. Тогда, полагая ^ = 0, найдем из равенства (49.6) С,1 + С2=1. Входящие в решения (49.6) и (49.7) постоянные С1? С2, Сэ п С4 являются, вообще говоря, комплексными величинами. Поэтому, обо­значая Ск = Bk + iDk (к= 1,2,3,4), можпо написать

В,+В, = 1, 1

/л+ £>а = о. І

Введем обозначения

E‘m еп’1 = с. (49.14)

Toi^ia

Л я

— mi ^ —«і г,

Е " = а — Ы е. " =— .

С

В конце первого участка функция At (zx) будет равна Л, ( £ ) = « (В, + В.2) — 2ID, + ІЬ (Вх — В2).

Нетрудно сообразить, что мнимая часть А^у^) рав­на пулю. Действительно, в конце второго участка функ­ция A2(zx) должна быть вещественной, так как ^(0) = = <XjА, (ті), а ах и А, (0) — вещественные величніші. ГІо изменение функции Л2 на втором участке связано с мно­жителями emz* п которые тоже являются вещест­венными. Следовательно, функция A.2(zx) вещественна па всем участке, в том числе п в начале участка. Но тогда, в силу неразрывности функции А [первое условие «склей­ки» (49.8)], можно утверждать, что Ax(zx) в конце своего участка тоже является вещественной величиной. Условие отсутствия мнимой части у А^ ~ ^ приводити равенству ВХ = В2,

Которое в совокупности с (49.13) дает В3 — = у.

Упоминавшееся только что требование, чтобы функ­ция А2 (zx) была вещественной всюду, позволяет найти еще две величины: D3 — D4 = 0. С учетом найденных значений Вх, В.2, D3 и D4 п с учетом условия Dx— — D.2 (49.13)’ равенство величин Ах (zx) и Az(zx) прн п = у выразится следующим образом:

А — 2hDL = cBs + ~ . Условие Аа (я) = aAj (0) даст: » •> , IU

А условие совпадения производных [последнее условие (49.8)]:

Система, составленная из трех последних равенств, по­зволяет найти D-р В3 н 2?4. Несложные вычисления дают следующее (приводим значения всех Bh и Dh):

Вг = 0,5, Dx = — 0,6; В3= -0,0392, D3 = 0,

В2 = 0,5, D2 = 0,6; Д, = 7,4, Д, — 0.

Таким образом, фуикция A(zx) определена. Соответ­ствующий график приведен па рис. 101. На этом же

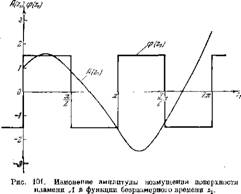
Рпсупке дана зависимость cp(zj). Если отвлечься от не­которого возрастания средней амплитуды A (z2) с тече­нием времени Zj (следствие неустойчивости), то можно говорить о том, что А (z,) является периодической функ­цией времени, которая достигает наибольших абсолют­ных величин приблизительно на серединах участков.

Характеризуемых положительными значениями ф^^иі2. Это означает, что наибольшее положительное возмущение суммарной поверхности пламени будет происходить в эти моменты времени.

Возмущение эффективной скорости распространения пламени 6U’crop (папо. мннм, что 6С/СГОр нрп увеличеиип абсолютной скорости сгорания является положительной величиной и отличается от бUx знаком) может быть па основе формулы (38,29) написано следующим образом;

Б^сгар-г/н. сг^ (Ifn. СГ — — Uu>0). (49.15)

Следовательно [см. (38.20), (38.24), (38.30), (38.31)], максимальное значение Ucrop? так же как и Л (z{), будет достигаться в моменты, которые соответствуют середине участков ф (zx) = т2.

Функция ф (zt) есть результат грубой идеализации функции 2q sin 2zx = 2q sin со£. Напомним [ото проще всего видеть из равенств (38.22), (38.24) и (38.25)], что вели­чина q пропорциональна действующим на поверхности пламени ускорепиям. Это позволяет связать колебания скорости сгорания bUCV0V с колебаниями скорости. Дей­ствительно, пусть колебания скорости в холодной части течения перед фронтом пламени равны

Bvx = — (fiascos ш£, (49.16)

Где (бо,)0 —амплитуда колебаний bvx. Тогда возмущение ускорения, действующего на фронт пламепп, запишется в впде

Bb = (o(6vx)0sme>t. (49.17)

Можно считать, что в принятой схематизации этот закон с точностью до масштаба изображен в виде функ­ции ф (Zj) на рнс. 101, при-этом максимумы бb соответ­ствуют серединам участков ф (zx) = т2. Поскольку максимумы абсолютных величин A(zl), т. е. максимумы волнообразования на поверхности пламени, а следова­тельно, и максимумы возмущений поверхности пламени бS, тоже совпадают с серединами участков ф (z2) = + т2 (с наибольшими значениями возмущений ускоре­ния ЬЬ), то фазовый сдвиг между 6iS* п ЬЬ равен нулю и, следовательно.

BS = (6ЛТ)0 sin t»t. (49.18)

Здесь (65)0 — амплитуда колебаний поверхности пла­мени. Заметим, что, согласно графику функции A(zx) на рнс. 101, существуют моменты, когда А (гл) становится равным нулю, а фронт пламени перестает быть возму­щенным. Очевидно, что прн этом S достигает минимума, т. е. указанные моменты соответствуют в приведенной записи 65 — — (65)0 (минимуму 65). Следовательно, «есте­ственным» состоянием фронта пламени считается неко­торая средняя искривленность, а наибольшими возму­щениями [соответствующими 65—-г(65)0 и 65 = —(650)] такие, которые либо удваивают эту среднюю искривлен­ность, либо сводят ее до нуля. В первом случае происхо­дит увеличение поверхности пламени против средней величины, во втором случае уменьшение этой поверх­ности.

Если обозначить входящую в формулу (49.15) величину относительного изменения поверхности пла­мени через bS — ^ , то, пользуясь уравнениями (49,16) и (49.18), можно установить фазовое соотношение между fiffoop и

Б^сгщ>= ^.егй sin ®t,

Л, Л * • Г, ‘М (48Л9)

6t’j = (61^)0 РІП {^(ot 2") • I

Как видно пз написанных равенств, сдвпг по фазе между bUCTOV и 6равен — у.

Рассмотрим вопрос о возбуждении акустических коле­баний в трубе, закрытой с одного конца, когда процесс возмущенного горения описывается первым равенством (49.19). У закрытого конца трубы пе может существовать средний поток акустической энергии, отличный от нуля. Поэтому колебания скорости 6ух и давлення bpj будут, при установившихся колебаниях, сдвинуты но фазе на ™ .

Это значит, что колебания скорости сгорания 6{7сгор бу­дут происходить в фазе пли в нротпвофазе с колебаниями
давления. Выше уже говорилось, что условия воз­буждения вследствие колебаний тенлоподвода и вслед­ствие колебаний bUcruр в основных чертах совивдают, а в § 45 было показано, что близость фаз У = Ы/СГ()р и бр} является иаиболее благоприятной для возбуждения акус­тических колебаний. В тех случаях, когда Ьрх и Ы/Сг0р находятся в нротивофазе, возбуждение акустических колебаний невозможно. Сказанное здесь следует, в част­ности, и из вида тппнчиой диаграммы границ устойчи­вости, приведенной на рис. 27.

А) —	Ж*"—
61-

Стности закрытого кон — Ряс. 102. Возмущения скорости те-

Ца трубы в момент чевпи в окрестности ванрытеи-о

4 ‘ — конца труиы. перехода возмущепия

Давления Ьру через мак-

Си лгум. И момент, непосредственно предшествующий максимальному сжатию газа, воздушные массы еще дви­жутся к закрытому концу (схема а), а в момент, непо­средственно следующий за максимальным сжатием газа у закрытого копца трубы, Начинают двигаться в сторону открытого копца трубы (схема б). Такой характер дви­жения говорит о том, что па газы действует ускорение, направленное в положительную сторону оси х. Поскольку в момент максимального сжатия возмущевпе скоростп б у, переходит через нуль, то в этот момент ускорение бb достигает наибольшей абсолютной величины [см. (49.10) л (49.17)].

Рассмотрим более подробно вопрос о том, когда фазы bUcr0p и Ьрг будут совпадать. На рпс. 102 дана схема движения газа в окре­

Таким образом, в. момент максимального сжатия у закрытого конца на газ, расположенный вблизи этой области сжатия, действует максимальное положитель­ное ускорепие. Физически этот результат кажется почти само собой разумеющимся. Максимуму положительного ускорения соответствует середина участка ф(гд) = +/«2, т. е. моменты, когда bS, а следовательно н ЬІ7сг0р, дости­гает максимума. Поэтому в блпжайшей окрестности 29 г,. В. Раутенбдх
закрытого конца всегда будет наблюдаться совпадапне фаз брх и 6*7crop, т. е. будут выполняться условия воз­буждения. Что касается других участков трубы, то возможность самовозбуждения колебаний при нахожде­нии фронта пламени в них существенно зависит от номера

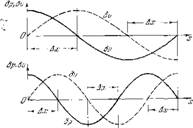
Рис. 103. Эшоры стоячих воля колебании для первых трех гармоник (труба с одним закры­тым концом); Дя —интервалы, внутри которых должен находиться фронт пламени, чтобы само­возбуждение оказалось возможным.

Бр. ди

Возбужденной гармоники. Чтобы рассмотреть этот вопрос несколько подробней, обратимся к рис. 103.

На рнс. 103 приведены эторы стоячих волн колеба­ний Ьр и bv для трех первых гармоник, причем эпюры bp ii б v условно совмещены в одной нлоскости. Как было тоЛько что ноказано, у закрытого конца (при ^=0) усло­вия возбуждения выполняются всегда, т. е. для всех гар­моник. Из предыдущего яспо, что в конечном итоге вопрос
ч возможности возбуждения свидится к вопросу о соотно­шении между фазами давления и ускорения; еслп поло­жительному 6/>j соответствует и л о ж ит е л ыю е б 6, то коле­бательная система способна возбудиться. Рассмотрим с этой точки зренпя вторую гармонику (средняя дна — грамма на рис. 103). В окрестности .х —0 условия возбу­ждения выполняются, при переходе эпюры bp через пуль они нарушаются. Действительно, нри этом Ьр мспяет знак, т. е. меняет фазу па п, в то время как фаза bb сохраняется [пз формулы (49.17) видно, что пзмепенпе фазы bb возможно только при изменении фазы (6i? j)0, а эпюра bv па рпс. 103 говорит, что при переходе через сечение, соответствующее Ьр = 0, фаза 6i> остается преж­ней]. Следовательно, если па участке, прилегающем к закрытому концу трубы, фазы и bb совпадали, то в окрестности, лежащей правее сечения, где Ьр~0, опп оказываются сдвинутыми на л. Это означает, что bp п bUcr0р находятся в протпвофазе п акустические коле­бания будут демпфироваться.

Дальпейшое движение в положительном направлении оси х приводит в сечение, где меняет знак (т. е. изменяет фазу на л) возмущение bis. Что касается фазы bp, то она остается прежней. Таким образом, справа от узла bv фазы bp її bb будут опить такими, что возбуждение акус­тических колебаний станет возможным. Следовательно, если первая гармояика, изображенная в верхней части рис. 103, допускала возбуждение системы нри любом положении фронта пламени внутри трубы, то для второй гармоники существуют две области, в которых возможно возбуждение — одна лежит в окрестности закрытого, другая в окрестности открытого конца трубы.

В нижней части рис. 103 построены эшоры стоячих во. тн bp и bv для третьей гармоипкп. Относительно при­веденных эиюр можно провести точно такпе же рассу — жденпя, которые показывают, что для третьей гармоники существует три участка, внутри которых обеспечиваются условия возбуждения, и два участка, где этих условий нет. Интервалы значений. с, впутри которых должен находиться фронт пламеып, чтобы появилась возможность возбуждения акустических колебаний, обозначены иа рис. 103 через Ах.

Полученный здесь па основе теоретического рассужде­ния результат хорошо совпадает с экспериментом. Для примера па рпс. 104 даны результаты опытов Коварда, Хартвелла и Джорджсона, уже приводившиеся на рис. 49 и рис. 50. Наряду с опытными точками на диаграммы нанесены зоны Ах, построенные следующим образом. Так как холодная смесь в рассматриваемых опытах была

HH

Ах

So

Рис. 104. Сравнение с експериментом иаіі денных теоретических интервалов Дх, внутри которых должен находиться фронт пламени, чтобы с а мо возбуждение оказалось возможным,

Неподвижна, то четверть длины стоячей волны возмуще­нии давлення и скорости равна ^ (я, — скорость звука в холодном газе, й — частота колебаний в герцах). Первая четверть волны, отсчитываемая от закрытого копца (от пачала коордппат на рисунке), считалась зоной, где возбуждение «возможно, а затем аналогичные области появлялись через одну (рис. 103). Частота колебаний Q, которая подставлялась в приведенное несколько выше выражение, бралась пз опыта.

Как видно пз рис. 104, возбуждение акустических колебаний происходило только тогда, когда фронт пла­мени находился внутри зоп Ах1). Это является хорошим

Ах

*) Может ян звать недоумение то, что для первой гармоники нптервал Аг по простирается до открытого конца трубы. Однако ;)то вполне закопомерло. При построении областей Ах на рис. 104
подтверждением сделанного в начале настоящего пара­графа предположения, что основным механизмом обрат­пой связп является взаимодействие акустических колеба­ний с волнообразовапием на фронте пламени и воздей­ствие отого волнообразования па эффективную скорость распространения пламенп.

Рис. 104 дает повод сделать еще несколько замечаний по вопросу о механизме возбуждения колебаний. Прежде всего следует указать па то, что концы участков Д.-с соот­ветствуют: левый — узлу скорости, правый — узлу дав­ления. Поэтому па концах участков Д. г система не может возбуждаться. То, что в узле давлення возбуждения нет, видно из правой диаграммы иа рис. 30 (следует лншь иомппть, что на этой диаграмме амплитуда возмуще­ния отложепа кверху, а следовательно 6£чтор будет направлено по оси абсцисс). При повороте бСсгор на угол ~ относительно 6 г.’, диаграмма границ устойчивости

Не дает в этом случае попадания конца вектора bUCTQV в область неустойчивости. В окрестности узла скорости колебательпая система не возбуждается потому, что вместе с уменьшением амплитуды колебаний скорости уменьшается (при заданной частоте) п величина ампли­туды смещений среды /?„, входящая в выражепие для т2 [см. формулу (40.3)]. Если считать, что длина волны на фропте пламени А. сохраняет порядок своей величины неизменной, то вблизи узлов скорости //г2 я» 0. В то же время выше было показано, что возбуждение волнообра­зования па фронте пламени возможно. тишь при т- > >1,39. Следовательно, не только нри положении фронта

Расчет велся для заданных экспериментальных частот по холод­ному г а. чу, так как для оценки колебаний bp и 6г> перед фронтом шіамоші незачем зпать характер колебании, в гОрячен пасти трубы. Поэтому правый конец области Дя для первой гармоники лежит там, где располагался бы узел давления в том случае, когда вся труба была бы занолпепа холодным газом, а колебания происхо­дили с наблюденной частотой. Фактически характер колебаний горячих газов справа от опытной точки (который здесь интереса не представляет) совершенно иной, так как там располагается горячий газ, кроме того, при переходе через фронт пламенп пара­метры колебаний тоже мешпотси, так что фактически узел давле­ния расположен, конечно, у открытого конца трубы.

Пламени в непосредственной близости от узла скорости, но и прн удалении пламени на известное расстояние от этого узла колебательная система возбуждаться не будет.

Опытные точки ложатся, в полном соответствии со сказанным, внутрь интервалов Ах, причем тенденция к смещению опытных точек к правым концам интерва­лов Д,*• указывает на то, что для возбуждения колебаний более существенный! является возмущение скорости, а не возмущение давления. Особенно показательны в этом смысле опытные точки, соответствующие положению фронта пламени непосредственно у закрытого конца. В этот момент колебания происходят с частотой второй гармоники, причем по мере приближения фронта иламепи к закрытому концу трубы процесс колебаний начинает явно нарушаться. Впешне это проявляется в исчезнове­нии регулярности, быстром падеппи частот колебаний.

Если бы механизм обратной связи был обусловлен какими-то физическими процессами, зависящими от дав­ления (например, изменение периода в функции давле­ния и т. п.), то но мере приближения пламени к закрытому концу никаких нарушений процесса колебаний не наблю­далось бы. Наблюдаемые отклонения от ожидаемого характера явления становятся понятными, если в основе механизма обратной связи лежит «таскание» фропта пла­мени колеблющейся средой. Тогда близость закрытого конца трубы должна резко нарушить всю гидромеханику такого «таскания» и вызвать отклонения от теоретической картины.

Выше, в §§ 28 и 29, рассматривался вопрос о скачко­образном изменении частот колебаний прп непрерывном изменен]иг длины горячей части трубы. Там соответст­вующие результаты были получены на основании фор­мальных соображений и никак ие были связаны с кон­кретным механизмом возбуждения колебаний. Анализ конкретного явлепия, произведенного здесь, приводит к той же закономерности, но теперь становится понятной внутренняя сущность этого явления. Если рассматривать постепенное движение фронта пламени от открытого коица трубы (абсцисса, равпая 5 м на рис. 104), то перво­начально (как это следует пз схемы на рис. 103) будут неустойчивы все гармоники (здесь не учитываются потерн). Однако колебательная система начинает возбуж­даться пе с первой, а с наибольшей возможпой (с уче­том потерь) гармоники. Это происходит потому, что для более высоких частот необходимое для самовозбуждения удаление от расположенного у открытого конца трубы узла бр происходит раньше, чем для более нпзкнх гар­моник. Как только в результате движения фронта пла — мепн к закрытому концу трубы амплитуда колебаний скорости bv уменьшится (вследствие приближения фронта пламепи к узлу bv) до соответствующей величины, про­исходит «перескок» на соседнюю гармонику, для которой узел bv расположен на более далеком расстоянии от откры­того конца. С этой точки зрения становится понятпым и повторный переход на колебания с частотой второй гармоники у закрытого конца трубы. Oif происходит тогда, когда переход на вторую гармонику «удаляет» фронт пламени от узла 6t> (совпадающего с закрытым концом трубы), причем это удаление надо понимать как смещонне относительно эпюры стоячей волны: в то время как самые левые экспериментальные точки, соответ-

1

Ствующие основному топу, лежат па расстоянии — — g-

Четвертн длины стоячей волны от узла скорости, для вто­рой гармоники на том же расстоянии от закрытого копца укладывается четверть длины волны целиком, т. е. фронт пламени оказывается в пучности б v.

Конкретный анализ рассматриваемого эксперимента делает понятным и то, почему экспериментальные точки на рис. 50 лучше совпадают с теоретическими областями неустойчивости, чем точки на рпс. 49. В § 29 по этому поводу можно было утверждать только то, что характе­ры возмущенного процесса горенпя в момент наступле­ния неустойчивости и в момент ее исчезновения не вполпе одинаковы. Теперь это общее замечание может быть конкретизировано: наступление неустойчивости связапо с удалением от узла давления, в то время как ее исчезно­вение обусловлено приближением к узлу скорости. Эти внешпне прнчшгьг имеют более глубокое физическое содержание. В момент наступления неустойчивости волнообразование на поверхностп пламени может легко возникнуть, лимитирующим является то, что вследствие близости фронта пламени к узлу давления отличное от нуля bUсгор не может дать положительного притока акустической энергии. В момент исчезновения неустой­чивости фронт пламени приближается к пучности давле­ния, условия получения положительного притока акусти­ческой энергии весьма благоприятны, но вследствие уменьшения j 6yj прекращает функционирование механизм обратной связи (прекращается волнообразование на фрон­те пламени). Из сказанного становится ясным, что при­чины начала и коица неустойчивости совершенно раз­личны; поэтому совпадепия теоретических и эксперимен­тальных границ исчезновения неустойчивости па рис. 49 и ие должно было получиться.

Полученные в §§ 28 и 29 результаты имеют преимуще­ство большой общности, поскольку они не зависят от конкретного типа вибрационного горенпя. Но будучи весьма общими, эти результаты не могут объяснить мно­гих частностей паблгодаемого явления. Не следует также забывать, что выводы § 28 основаны па предположении, что область неустойчивости существует. Выводы настоя­щего параграфа, в этом отиошенин, более полны, они говорят, что для рассматриваемого режима горения область неустойчивости должна существовать.

В заключение полезно еще раз вернуться к рассмот­рению экспериментальных данных, чтобы проанализиро­вать их с точки зрения генерирования акустической эпергии в зопе теплоподвода.

Поскольку при вибрационном горении рассматривае­мого типа осповпьтм является возмущение эффективной скорости распространения пламени, условие на поверх­ности разрыва 2, представляющей область теплоподвода, надо написать в виде системы (16.12). С учетом равенств (15.9) н (15.10), а также в предположении, что средняя скорость перемещения фронта пламени по трубо весьма мала, а следовательно Mt и М2 близки к нулю, систе­му трех уравнений (16.12) легко привести к следующему виду.

Pt=Pv

(49.20)

Вместо трех уравнений (16.12) получены два уравне­ния (49.20), потому что первое и третье уравнения (16.12) после введения предположения Л/j s= Л/"2 = 0 совпали.

Суммарный поток акустической энергии, излучаемой зоной теплоподвода, можпо определить но равенству (19.7), положив в нем т= 1. Тогда с учетом условий (49.20) и заметив, что 2}il i — получим

As = y (l-w1)!^. (49.21)

Как уже указывалось, 6 L и б Ї7сггф отличаются только знаками. Следовательно, переходя к безразмерным переменным, можно написать

V —

Еслп учесть равенства (49.19) и положить, что для участка типа b на рис. 96, который соответствует тече — пшо, прилегающему к закрытому концу,

Б//"] = {bpx)0 .«in соt, то можно утверждать, что

»11 Рі і

Подставим найденное значение в (4!).21). Тогда

3»=4 (»» — 1) ^f — (Щ0 |Я|. (49.22)

Для участков типа а на рпс. 96 знак As будет противо­положным тому, который дает формула (49.22). Посколь­ку п > 1, система будет возбуждаться лишь на участках тпна Ь.

Полученная здесь формула (49.22) является аналити­ческой записью того факта, который уже подвергался обсуждению песколько выше — возбужденно вибрацион­ного горенпя (т. о. получение положительной секупднои работы Лі;) связано как с наличном отличного от пуля возмущения давления /?,, так и отличного от нуля волно­образования на поверхностп пламени (6£)0. Если раньшо ото заключение основывалось на чисто качественных соображениях о типичных конфигурациях границ устой­чивости, то теперь оно приобрело количественный харак­тер, указывающий па то, что оба эти фактора играют одинаково важную роль. Следует па помнить, что при вы­воде формулы (49.22) уже были приняты должные фазо­вые соотношения, поэтому онп ие вошли в окончатель­ное. выражение для Л^.

Для того чтобы стало возможным волнообразование па поверхности пламени, как уже говорилось, параметр т2 должен быть больше 1,4, по меньше 9. Если обра­титься к выражению для т2 (49.3), то после перехода от h0 к (буД, = й0со получим условие волнообразования в виде неравенства

Из которого следует, что колебания скорости bv должны превосходить некоторый предел. Поэтому (б5)0, отлич­ное от нуля, может существовать лпшь в известном уда­лении от узла скорости. Надо заметить, что более точ­ная численная оценка этого обстоятельства по результа­там эксперимента затруднительна, поскольку в нем пе было получено данных о длине волны на поверхности иламепи X.

Вторым затруднением при анализе выражения (49.22) является то, что входящая в пего сомножителем величи­на (6iS)0 не определяется параметрами акустических ко­лебании. Если условие (49.23) выполнено, то при по­стоя ппых колебаниях среды [постоянном (6у,)0] величина (bS)0 может изменяться со временем. В § 38 это обстоя­тельство уже подчеркивалось, и там указывалось, что такое свойство волнообразования связано с тем, что обра­зование волн па поверхности раздела является парамет­рическим резоиапсом. Поэтому — хотя по мере отхода фронта пламени от узла давления (перемещения справа палево внутри интервалов Ах па рпс. 104) амплиту­да (6yj)0 будет монотонно уменьшаться, амплитуда (bS)0, характеризующая волнообразование, может возрастать. Следовательно, и произведение (bS)n | р, входящее.5 50] колр. баішя В 1IT. I ДЕ мюльных топклх 459

В формулу (49.22), может увеличиваться пе только за счет возрастания l/’iJ, но и за счет возрастания (бS)0. Увели­чение Ац по мере удаления фронта пламени от узла дав­ления будет приводить к тому, что амплитуды акустиче­ских колебапий станут возрастать. Это возрастание общего уровня колебаний будет в свою очередь воздействовать на величину w.2, так что изменение амплитуд колебапий по мере перемещения фронта пламени по длине трубы пе будет столь закономериым, как изменение частот.