В предыдущем параграфе был проанализирован одни из возможных случаев возбуждения акустических колебаний горением. Рассмотрение было проведено без учета запаздывания тепловыделения. Можпо было бы вернуться к этому случаю и выявить то новое, что дает учет запаздывания. Однако более целесообразным представляется рассмотрение другого примера, такого, где роль, которую может играть задержка воспламенения, проявилась бы наиболее ярко. В качестве подобного примера рассмотрим спстему, которая при отсутствии запаздывания, в отличие от описанной выше, вообще пе возбуждается.
‘) В камерах сгорания следует различать коэффициент избытка воздуха, подсчитанный для камеры в делом, и местиое значение а в зоне горения. Суммарное а бывает нередко выше единицы за счет воздуха, направляемого в обход зоїш горения и подмешиваемого к продуктам егорапия ниже зопы интенсивного горения.
Пусть ПлоскостЬ подвода тепла X лежит во входном сечении, т. е. /,—-0. Тогда продукты сгорания займут всю длину трубы, чему будет соответствовать 1г~ (рис. 42). Краевые условия сформулируем так: на входе и выходе трубы расположены узлы скорости. Такие краевые условия могут рассматриваться, панрнмер, в качестве первого приближения к реальным краевым условиям, наблюдаемым в камерах сгорания жидкостных реактивных двигателеІІ. Л нижней части рис. 42 дана схема типичной камеры такого двигателя. Слева, на так называемой головке камеры А, располагаются форсунки, подающие компоненты топлива — горючее и окислитель, а в правой части камеры сгорания помещается сопло Лаваля. Очевидно, что глухая стеика А не позволяет колебаться скорости течения у левого конца цилиндрической части камеры (расход компонентов топлива считаем постоянным). Справа, в критическом сечении сопла Лаваля С всегда сохраняется скорость течения, равная скорости звука. Если отвлечься от возможного колебания самой скорости звука, то можно считать, что в сечении С поддерживается постоянная скорость течения. Когда расстояние от В до С мало, ото прпводпт к тому, что в сечении В скорость течепия также становится постоянной. Отсюда возникает формулировка второго краевого условия—отсутствие колебании скорости в правом кон цевом сеченнп (В) цилиндрической части камеры сгорания. Заметим, что близость написанных краевых условий к крае вым условиям для камеры сгорапня жидкостного реактивного двигателя ие означает, что далее будет дан анализ устойчивости рабочего процесса в таком двигателе. Этому будет иосвящеи ниже специальный раздел книги. Здесь, вероятно, нелишне указать, что неустойчивость сгорания в жпдкостпом реактивном двигателе связана в первую очередь с возмущением расхода массы, а пе теплоподвода.
Будем описывать процесс возмущенного теплоподвода в плоскости 2, совпадающей с сечением А на рис. 42, уравнениями (17.5) с учетом условия я, = 0 и формул (24.1),
Е [
![]()
ВС
Рис. 42. Идеализированная схема жидкостного реактивного
ЛШ1ГІІТЄЛЯ.
Vi*
(24.2), т. е. предположим, что в области теплоподвода имеет место только возмущение притока тепла и нет колебаний фронта пламени и т. п. Учтем также, что по краевому условию і’г=0. Тогда условия на плоскости 2 запишутся в виде
Р.> = а„рх A23Qppv J
Где «12, a is, an u «.23 — некоторые постоянные. Надо сразу оговориться, что эта запись справедлива лншь в том случае, когда изменение процесса горения мгновенно следует за изменением давления pv Если же процесс горения будет отставать от воздействующего на него давления рх на время Дт, то вместо равенств (26.1) надо написать другие. Первые слагаемые в правых частях этих равенств пе претерпят изменения, зато вторые, связанные с процессом возмущения теплоподвода, надо будет брать такими, какими онп были в момент, отстоящий от рассматриваемого па время Дт. Это можно зависать следующим образом:
V3{x) = a12p1 (т) J Дт), ) /1(. ,
_ > (26.2) Р» ("О = ашРх (*) т (hzQvPi (т — Лт). )
(Стоящие в скобках величины т и т —Дт указывают, для какого момента времени берутся переменные.)
Как известно из предыдущего, в принятой постановке задачи изменение всех возмущенных величин происходит пропорционально Поэтому формулы (26.2) можно
Переписать в следующем виде {v2i) = v2 при т = 0 н т. д.):
Ур = «.л/’ + ]
Отметим, что при Put индексы «единица» или «два» не поставлены вовсе. Дело в том, что хотя масштабы времени в холодном п горячем участках течения п различны (так как онп зависят от скорости звука) н поэтому следует отлпчать ^ от (}2. а от т2, произведение |5т не зависит от избранного масштаба времени, так как единица времени входит в одном из этих сомножителей п знаменатель, а в другом —в числитель. Сокращая оба равенства (26.3) на <>№, придадим условиям на S с учетом запаздывания окончательный впд:
— — — (2h.4)
Р,(1 = а22р10 4 I
Прп записи приведенных равенств уже использовано первое краевое условие (i^sO), Второе краевое условие — ~ог = 0 при £=•/., = 1 даст, на основании первой формулы (4.13).
TVPi(i) + /’йпЧ-2 (I) = <>.
Подставляя в последнее равенство с20 и /;.,„ из (2В.4), получим после некоторых упрощений
(«„ + ( 1 — г®щ) = <2«-й)
(В дальнейшем индекс «2» прп Р будем для простоты опускать.)
Следует подчеркнуть, что условия па 2 в случае учета запаздывания (26.4) в отличие от условий па 2 для случаев, когда задержка во времени не учитывается, становятся зависимыми от комплексной частоты {}. Ото обстоятельство затрудняет решение характеристического уравнения. В частности, метод, изложенный в § 23, оказывается неприменимым, так как в равенстве (23.5) коэффициенты Cj, С2, Сз и Сj становятся функциями комплексной частоты р. В этом случае соотношения (23.7) неверны, поскольку они были получены в предположении вещеетвенностп С1} Сг, С5 и С±. Перепишем (26.5) в впде
где Л({5) иБ((3)—вещественные величины. На границе устойчивости Р = ш и тогда написанное равенство разбивается на два, связывающие только вещественные переменные Qtl со.>соДт = Л (со), | Qtl s’i її соДт = -)і{ь>). j Отсюда сразу находим
Irctg j Л (со)
/,’Л.
(2ІІ.7)
Cos соДт ‘ I
Где к — целые числа. Задаваясь различными значениями со, находим по первой формули соДт, а по второй Q Таким образом, оказывается возможным найти пары значе — Јt>Jr
Qn =
ІОО &
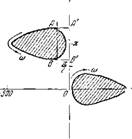
Рно. 43. Диаграмма устоіічішогтп при u, n — л л 111 я а пня’ды папип Дт.
Вий Qp и Дт, удовлетворяющие условиям существовании границы устойчивости.
(2В. И)
Цт) ‘ ■ I (и) J
ОДт —
На рис. 43 даны результаты такого расчета для — = 0,1, М2 — 0,25. Как видно из графика (к — 0; к = 1), неустойчивость возможна лишь для двух типов чередующихся замкнутых областей в плоскости (Qp, со Дт). Эти области сдвинуты друг относительно друга (по оси со Дт)
на угол, равный я, и соответствуют значениям Qp разных ішаков. Существование таких именно типов областей для рассматриваемого случая можпо было легко предсказать па основе диаграммы, приведенной в левой части рис. 28. Действительно, полагая QpewilX=Q, сведем рассматриваемый случай к исследованному выше. Соответствующая диаграмма у сто йчи в ости типа представленной на рис. 28 дана пл рис. 44, где аргумент вектора Q в области неустойчивости изменяется от —0 до + О (направления ОВ и ОЛ). С учетом последнего равенства легко получить, что значенням Q > О области неустойчивости отвечают следующие границі, і для Лт:
— О < ш Лт < 0. а значениям < 0 —
Л — 0 < соДт < 6, что находится в полном соответствии с результатом, показанным па рис. 43.
Хотя результат, представленный па рпс. 43, и можно было предвидеть, оп был получен здесь путем численного апализа уравнения (20.5) главпым образом для того, чтобы проиллюстрировать на простом примере метод решения задачи о возбуждении акустических колебании теилоподводом с учетом запаздывания процесса возмущенного теплоподвода. В более общих случаях такой простой анализ условии возбуждения прп помощи диаграммы типа представленной на рпс. 44 затруднителен. Кроме того, не следует забывать, что полученный в настоящем параграфе результат содержит пе только сведения о положении границ устойчивости, но и о частотах, соответствующих отдельным точкам отих границ.
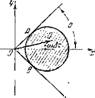
Рис. 44. Влияние запаздывания At на положение вектора Q на диаграмме устойчивости.
Рассмотрим приведенную па рис. 43 диаграмму более подробно, наложив па задачу дополнительные ограничения. Предположим, что по физической сущности процесса теплоподвода Qp может иметь лишь отрицательные значения. не Превосходящие по абсолютной величине 100.
Тогда возбуждение системы окажется возможным лишь в тех случаях, когда изображающая точка на диаграмме рпс. 43 будет лежать в заштрихованной части прямоугольника АА’ВВ’. Это обстоятельство накладывает специфические ограничения на допустимые зпачення Дт. Чтобы показать это. построим на рпс. 45 связь между Дт и со, снимая с дна — граммырпс. 43 значения соДт п со, соответствующие участку
Ат

0/2 J І І В *oj
1’ш 45. C. iw. sl между navTOTrtNUi колеоашш w її величиной запаздывания Дт.
А Н границы устойчивости. Как видно пз рис. 45. возбуждение оказывается возможным лишь при определенных частотах со п требует ири этом вполне определенных значении Дт. Важно при этом отметить, что если по рассматривать очень больших со (они почти всегда нереальны), то система не может возбудиться при Дт, близких к нулю. Это является весьма существенным отличием рассматриваемой задачи от задачи предыдущего параграфа, когда система была способна к возбуждению и при Дт = 0. Таким образом, учет запаздывания может оказаться необходимым, н это обстоятельство следует принимать во внимание.
Чтобы закончить рассдіотренде вопроса о влиянии дС — на возбуждение колебаний, сделаем одно замочапие. На рис. 45 приведены только минимальные значения Дт, необходимые для возбуждения колебательной системы. £сли увеличить Дт таким образом, чтобы повое значение т—Ат’ было связано с приведенным па рис. 45 Дт=~Дт(| соотношением соДт’= соДт0-г2Л’Я, где к — целое число, то па диаграмме рпс. 44 изображающие точкп для этих двух случаев, очевидно, совпадут.
Следовательно, при непрерывном изменении Дт от О до со могут периодически чередоваться области значений Дт, для которых система устойчива, с областями значении Дт. для которых система неустойчива.
§ 27. Частоты колебаний
При анализе частот колебании, возбужденных теилоподводом, следует учитывать, что в этом случае закономерности возбуждения частот не столь просты, как в обычных акустических системах. Выше это обстоятельство уже подчеркивалось в связи с примером решения характеристического уравнения {§ 23). Там, в частности, говорилось, что отклонение частот колебаний от величин, предсказываемых простейшими акустическими формулами, связано с тем, что нрн перосеченпп акустической волной поверхности разрыва 2! лишь часть ее проходит в область с иной температурой, а другая часть отражается от поверхности разрыва.
Дело пе только в том, что по разные стороны £ течет газ с различными температурами. Процессы, идущие в лоне горения (т. е. формально — свойства поверхности 2), самым существенным образом влияют на величины возбуждаемых частот.
Рассмотрим это явление более подробно. Пусть система находится па границе устойчивости и совершает колебания с постоянной амплитудой (v = 0). Для определенности предположим, что система пмеет узлы давления слева и справа от плоскости подвода тепла 2, в сечениях с координатами и Пусть plt щ и р2, ^-возмущения давления п скорости на плоскости 2 (£ = 0) слепа
и справа соответствснпо. Тогда исходная система будет иметь следующий вид:
TVPi(Јi) т/’іФіІІіІ^і),
Г’гФ* (Sa) (І2)=0.
Условия на S запишем в канонической форме (17.1):
P-i~ (l> йХ) = Uh — і" УтРх)%
Где чпсла ух н у2 введены (как и выше в аналогичных случаях) для того, чтобы явпым образом связать величины бЕ и ЬХ с фазами п амплитудами колебаний системы. Эти чпсла являются формальным введенном некоторой обратной связи, конкретизация которой здесь не требуется.
Используя (27.2), преобразуем характеристическое уравнение системы (27.1) к следующему виду:
А и — Фі Fo) Фі (Ь) ,, _ Фі (Si) _ Фі (S2) r>7 — JV " Уї Фа (Ыф®<Св) п Фг(£і) ‘ W " }
Отношения функций! Ц|> входящие в написанное урав — Ф2
Пение, можно определить па основе формулы (22.-3). Положив р = ш (по условию v = 0) и обозпачпв
(27.5)
(27.4)
I —Лі2
Нетрудно получить, что Фі(6) _
Проанализируем, основываясь на уравненин (27.3), оба простейших случая возбуждения колебаний — один, характеризуемый условием ЬХ = 0 (уг = 0), другой — условием ЬЕ = 0 (^1 = 0). В обоих случаях, как это следует из формулы (27.5), в правой части равенства (27.3) будет стоять мппмая велнчппа, а коэффициенты при ух или у.,
В левой части будут вещественными. —-
Таким образом, нейтральные колебания реализуются прп мнимых значениях и у2, что указывает на нзвест-
пью уже из § 12 и 22 условия возбуждения колебаний, согласно которым сдвиг по фазе между ЬЕ и pY (пли между ЬХ и t’j). равный, соответствует границе устойчивости. Этот результат не зависит, конечно, от величі и ты частоты колебапнй.
Рассмотрим, какие час юты могут возбуждаться в изучаемой системе. Изменение величины (о ведет к нзмепе-
|
Шх Зі |
М |
||
|
Гі |
|||
|
Ї |
F L _ |
||
|
А |
, я/", fM- |
||
|
Ч/ |
Г з 1s в 7 |
, Я Ш ш |
|
|
-гі |
— |
||
|
-Зі |
— |
||
|
-it |
— |
‘ле Idr |
Гис. К» і >н|’і’.имение собственны* частот колебателг.- пой системы.
Нищ а (27.4). а следовательно, л функции и
Фз^бп Фз U2)
(27.о). Таким образом, каждому значению со соответствует с вис значение?/, (или у2), нрн котором возможны нейтральные Колебания системы с заданной частотой о; оно племеитарпо определяется из уравнения (27.3).
Чтобы проиллюстрировать сказанное, па рис. 40 приведены результаты подобного вычисления. Для большой наглядности используются не значення у{ и у2, а ЬЕ=у1р] и 6X=y2v1 (при этом p-i н считались вещественными и положительными). Расчет произведен для случая трубы с узлами давлення в концевых сечеппях и с плоскостью 2, расположенной на равных расстояниях от обоих копцов. Скорость течения в «холодпой» части характеризуется числом М = 0,15, а относительный подогрев Т02/Т01 — (3,25 (здесь !Г0 означает температуру полностью заторможенного газа). В расчетах величина v в «холодном» концевом сечении была условно принята равной единице.
Важнейший вывод, который следует пз уравнения (27.3), сводится к тому, что при должном изменении ЬЕ или 6А~ можпо получить любую наперед заданную частоту (этот факт был З’же использован в § 24 для построения границ устойчивости, где определялось изменение Q и Qr при непрерывном изменении со). В отличие от обычиых задач акустики частота колебании определяется здесь не только свойствами колеблющегося газа и размерами трубы, но и характером процесса теплонодвода на Z. Поэтому такие понятая как «основной тон колебаний» пли «обертоны» следует употреблять с осторожностью. Эти привычные понятия имеют смысл для наперед заданных фиксированных значений ЬЕ и ЬХ. Действительно, например, прп ЬЕ — ЬХ -0 пз всех частот, приведенных на рпс. 46. могут реализоваться только частоты, соответствующие точкам А її /І. Частота со =4,82 (точка А) может рассматриваться как первая гармоника, частота со —7,95 (точка И) как вторая и т. д. (другие гармоники па рис. 46 не приведены). При другом характере процесса па например ЬЕ = ЬЕ0, те же гармоники будут соответствовать точкам А’ и 1Ґ. При непрерывном изменении ЬЕ возможен непрерывный переход от первой гармоники ко второй.
Здесь рассматривались элементарные случаи возбуж — депия колебаний, ирп которых ЬЕ пли 6Х равно нулю. Однако полученные выводы пе изменяются и в общем случае, когда между ЬЕ н ЬХ существуют произвольные соотношения. В этом легко убедиться на основании анализа уравнения (27.3).
§ 28. Ступенчатое изменение частот колебаппй с изменением положения зоны горения
Экспериментаторам хорошо известно о существовании связи между положением зоны горения (длиной «горячен» части трубы) и частотами колебаний. Известно, например, что при распространении пламени в трубе, заполненной горючей смесью, возбуждаемые пламенем частоты скачко — 2В СТУПЕНЧАТОЕ ИЗМЕНЕНИЕ ЧАСТОТ КОЛЕБАНИИ 22 t
Образно меняются по мере перемещения фронта пламени вдоль трубы. Это свойство легко поддается анализу на основе характеристического уравнения рассматриваемой задачи. Замечательным является при этом то обстоятельство, что подобное скачкообразное изменение частот никак не связано с конкретным видом процесса горения; оно может не наблюдаться лишь тогда, когда механизм возбуждения является фупкцией положення зоны гореиин вдоль оси трубы или функцией частоты колебании. Рассмотрим ;iTo явление более Подробно.
В качестве краевых условий выберем узлы давления ИЛИ скорости В сечениях Е = І! слева от поверхности подводи тепла и 1 = |2 справа от нее. Таким образом,
/?=|> или у = 0 ирit £ = Іі н | = Е3. (2H. J)
При использовании краевых условий вида (28.1) можно в решении не учитывать волн энтропии, и, если дополнительно условиться, ЧТО. S’j = 0 и формулы связи между
Рх и v.2, р., на 2 пе содержат ни комплексной частоты колебаний р, ни расположения плоскости 2 по оси трубы, то величины Е и р будут входить в характеристическое уравнение только через функции срх н ф2.
ГГрн этих предположениях два краевых условия (28.1) дадут два уравнения, связывающие, например, рг и vt в плоскости 2 [подобие тому как это получилось в § 23 при составлении характеристического уравнения (23.4)]. причем множители при р} и иг будут линейными функциями cpj ц ср2. Это даст в конечном итоге характеристическое уравнение вида
І «і. Фі (£і) + «12ф2 (У ад, (У + «з (У j =
Где вещественные коэффициенты alk будут функциями свойств поверхности 2. Вещественность коэффициентов предполагает запись условий на 2 ло типу форл/ул § 23.
Если учесть, что функции (р! и ср., линейно зависят от двух выражений, содержащих | и р (4.14)
Exp f-r^LV expJPL_ 1 V J ‘ lxP і — м ‘
То, выноси за знак определителя в первой строчке велн-
PlSl — f — 02&S Л
Чину е. хр -.J ^^ , а во второй — величину ехр ■ ^ J и сократив на нпх, получим характеристическое уравнение, зависящее от выражений
Как известно, величины [5, и рг связаны соотношением (22.5), а если начало отсчета £ совместить с S (рис. 22), то и удовлетворяют равенству
С учетом сказанного характеристическому уравнению (28.2) может быть придан следующий вид:
Здесь У»— целая рациональная функция второй степени с вещественными коэффициентами.
Проанализируем решение этого уравнения. Оно дает изменепне [3j в функции относительной длины «горячего» участка которую будем ниже обозначать 1.2, при заданных неизменных краевых условиях вида (28.1) п условиях на 2 указанного выше типа. Пусть по мере увеличения h величина декремента затухания колебаний v будет увеличиваться, переходя через нуль. Это будет соответствовать переходу от устойчивости (у < 0) к неустойчивости (v > 0). На границе устойчивости v = 0 и Р = гю[6]). Выберем пару значений /2 и ш, соответствующих границе устойчивости, и обозначилі их и юс1). Имея эти две величины, легко определить все множество значений пар чисел /2, ш. соответствующих всем гармоникам системы в момент перехода через границу устойчивости при увеличении /2. ,
Действительно, прп Р = гш равенство (28.3) становится равенством, связывающим тригонометрические величины
П Г 2м (І-/,) , • . 2w(J — М I
По условию оно удовлетворяется при /2= /j1′ П 0) = оУ’ Но тогда оно будет удовлетворяться так же нри всех значениях со и L, для которых справедливы равенства:
2<о(1-/а) 2м">(1_/.П) j
L-.V? 1 — М 1
О, О м„<„ • (28.5)
2(0/2 — 2Лгя 4- — 2 і 1 ‘
П{і-М) " — л(1—Л/1)’ |
Здесь К и Лг —любые це.1гые числа, ограниченные естественными условиями Q) > 0 и 0</3<1.
Следует лишь добавить, что знаки у вторых слагаемых надо брать одинаковыми —либо в обоих случаях плюс, либо в обоих случаях минус. В первом случае в левой части равенства (28.4) сохранится то же комплексное число, что и соответствующее 121′ и ша>, во втором появится сопряжепное комплексное число. Поскольку в правой части равенства (28.4) стоит пуль, это требует равенства нулю вещественной и мнимой частей числа, стоящего слева. Однако абсолютные величины как вещественной, так и мнимой части сопряженных комплексных чисел совпадают. (Это обстоятельство и позволяет писать в равенствах (28.5) два знака.)
Решив систему (28.5), находим:
О) = я[(1-А/;)ЛГ + л(1-Л/|)Л*] + ш(1 1
T _ЛП(1 — Щ) у J" (28.6)
2_ © " ‘ I
Может оказаться, что величины a>(17!;1, и юш велики, и для отыскания всех возможных комбинаций 0</2<1 и о) > 0, соответствующих границам устойчивости, окажется необходимым орать отрицательные значения целых чисел /V и Л. Чтобы избежать этого, и иметь в дальнейшем лишь положительные или равные нулю Л’ и К, можпо применить такой прием. Запишем /V и К в виде К — = K’=fK" и N = N’TN где числа К К"> N Л7" — целые неотрицательные. Тогда формулы (28.6) примут следующий вид:
Iii =■ л [(I — М’) К’}i (I — л/’^д-‘) 4-
I Л* (I—
— "" со
Здес ь
< = *>п’ — л [(І — М]) К" + «(1- Щ) — VI.
О= го"1/;1′ — л/? (і — .u®) N".
Числа К" и Л"’ надо выбрать так. чтобы
О < < я (I — Щ): 0 < < я// (1 — МЦ
Тогда К’ и Л" пе смогут быть отрицательными, так как в противном случае а) п 1г стали бы припимать отрицательные значения, что противоречит условиям, принятым вьппе.
В дальнейшем будем (кроме мест, оговоренных особо) предполагать, что в формулах (28.0) уже произведены соответствующие пересчеты, т. е. и Іь) имеют минимально возможпые значення. Иногда определенные таким формальным методом величины ffl(1} и не имеют физического смысла (со^ получается очень близким к нулю, а /У; > 1). Этпм не следует смущаться, так как подобный результат говорит лишь о том, что реально эти режимы (соответствующие А’ —0) наблюдаться но будут.
Рассмотрим сначала те решения, которые получаются при использовании знаков илюс в формулах (28.6). Тогда, задаваясь различпымп значениями К и N, можпо получить все грапицы устойчивости того же типа, что н исходная граница устойчивости, соответствующая и Это следует понимать в том смысле, что если, панрнмер, с увеличением U процесс пз устойчивого стал неустойчивым, то и все другие границы устойчивости ш; U, полу — ченпые на основе равенств (28.6), будут соответствовать переходу от устойчивости к неустойчивости по мере увеличения I.,.
Использование зиаков минус в (28.G) приведет к получению границ устойчивости противоположного по сравнению с исходной границей типа. Тогда, например, если С увеличенном z2 при переходе через І2] процесс из устойчивого становится неустойчивым, то все границы, полученные из равенств (28.0) ітрії отрицательных знаках у ш(|) 1>и и будут соответствовать переходу от неустойчивости к устойчивости по мере увеличения /2.
Указанное здесь свойство границ устойчивости легко доказать. Для этого достаточно сделать предположение, что при непрерывном измеиепии /2 комплексная частота р для всех гармопик также изменяется непрерывно (при этом отбрасывается неинтересный случай, когда прп всех /3 v=0). Предположение это вполне естественно, поскольку — свойства поверхности 2 были припяты иеизменными. Ко тогда очевидно, что при непрерывном изменении 12 следящий за одной и той же гармоникой наблюдатель будет отмечать, вообще говоря, многократные переходы через граппцы устойчивости, в моменты, когда будут удовлетворяться равенства (28.5). Важпо при этом отметить, что точки (1г, со), соответствующие границам устойчивости, полученные при использовании знаков «плюс» и «минус» в формулах (28.6), будут чередоваться. Это видно, например, из второго равенства (28.5), если заметить, что второе слагаемое правой части по абсолютному значению меньше 2л по определению. Действительно, второе уравнение (28.5) дает в плоскости (/2; со) пепересекающиеся гиперболы, которые, чередуясь, принадлежат двум семействам гипербол, получающихся при использовании знаков «плюс» и «минус» в указанном уравнении. Пересекая кривую ш = со (Z2), принадлежащую некоторой гармопике системы, эти гиперболы определят точки, соответствующие v=0, которые, чередуясь, будут принадлежать то одному, то другому семейству гипербол.
Выше было сделано предположение о непрерывном изменении Р в функции U. Тогда, прп монотонном изменении колебательная система, пересекая границы устойчивости, будет попеременно становиться то устойчивой, то неустойчивой (здесь не рассматривается вопрос о возможности реализации таких колебательных систем, у которых две точки, соответствующие соседним границам устойчи — 15 с. В. Раушенбах вости, будут стягиваться в одну точку). Следовательно, переходя через границы, соответствующие одному семейству гипербол, колебательная система будет всегда становиться, например, из устойчивой — неустойчивой, а пересекая границы, соответствующие другому семейству гипербол, из неустойчивой — устойчивой. Это утверждение п подлежало доказательству.
Приведенные рассуждения можно сделать более наглядными, ес-ли дать графическую интерпретацию формулам

Рис. 47. К построению диаграммы зависимости возбуждаемых частот от положения 2 по длине трубы.
(28.6). Обратимся с этой целью к рис. 47, па котором для некоторого численного примера построены линии равных К и равпых N в предположении, что Кроме того,
Здесь же папесены зависимости ш от 12 для разных гармоник (номера гармопик помечены прп них римскими цифрами), в предположении, что справедливо простейпгее_ акустическое правило для трубы с открытыми концами: пе — "~рпод колебаний равен времени двукратного пробега акустическим импульсом всей трубы (без учета взаимодействия "с зоной теплоподвода), т. с. что частота
F
1 — MV п (1 —М)
Задавшись затем некоторыми отличными от нуля значениями о)(1> и md) получаем границы устойчивости при использовании обоих знаков в формулах (28.6). Точки, соответствующие границам устойчивости, условно соединены прямыми, которыми отмечены области неустойчивости. При этом точки А0 соответствуют границам устойчивости, полученным для 7V=0, Ах и для N = 1 и т. д. Точки А соответствуют использованию знаков минус, точки В — знаков плюс в формулах (28.6). Как видно из
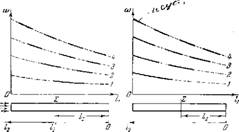
Рис. 48. Связь между положением 2 по длине трубы и всыиуж — даемымп частотами колебаний.
Чертежа, внутри каждого криволипейного четырехугольника, образованного лилиями равных К и N, лежит одна область неустойчивости.
Основываясь на сказанпом, легко построить Диагр&м- мы, дающие наглядное представление о распределении областей устойчивого и неустойчивого прптекапия процесса сгорания при перемещении зоны гореппя вдоль осп течения: Подобное построение дано на рис. 48 для двух типов кРаевЫх условий: ,трубы с открытыми копиами и трубы. С" одним закрытым концом. Отложенные по оси абсцисс значення /2 дают положение зоиы горения, по осп ординат отложены частоты колебаний со. Собственные частоты системы даны пунктирными линиями, около которых поставлены номера гармоник. Области неустойчивости показаны
Vj*
Сплошными линиями. Для того чтобы показать различные возможные типы распродолепия областей неустойчивости, па правой диаграмме приводен случай, когда основной топ имеет только одну, а не две границы. устойчивости. Такой случай вполне вероятен для трубы с одним закрытым концом.
Общие закономерности, которые бросаются в глаза при рассмотрении диаграмм, приведенных па рис. 48, могут быть сведены к двум положениям.
Во-первых, чем выше помер гармоники, тем большее число чередующихся областей устойчивости п неустоичп — востн помещается па длине трубы (при этом первая гармоника имеет одну область неустойчивости, вторая — две, третья — три и т. д.). Во-вторых, впдно, что одновременно могут быть неустойчивыми несколько гармоник, причем прп положении фронта пламени у открытого конца все гармоники устойчивы (хотя для высоких гармоник области неустойчивости и подходят сколь угодно близко к открытому концу).
При обсуждении этих диаграмм следует иомннть, что они получепы в предположении отсутствия излучения энергии пз открытых концов (узлы давлення в качестве краевых условий). Известпо, однако, что с увеличением частоты колебаний количество эпергпи, излучаемой пз трубы в окружающее пространство, резко возрастает (более подробно этот вопрос будет рассмотрен в следующей главе). Учет рассеивания энергии прп взаимодействии акустических воли с концами трубы приведет к тому, что области неустойчивости по мере увеличения частоты колебаний начнут сужаться, и начиная с некоторой частоты совершенно исчезнут. Следовательно, высокие гармоники практически наблюдаться пе будут п при положении фропта пламени в некоторой, достаточно большой, окрестности открытого копца трубы процесс будет всегда устопчпв.
В птоге можно предсказать следующий общий характер протекания процесса. По мере удаления зоны горения от открытого конца первоначально стабпльпый процесс должен стать пеустойчивым, причем частота колебаний будет скачкообразпо понижаться до основного тона системы. Это приведет к, казалось бы, парадоксальному поведению колебательной системы: увеличение относительной длины участка трубы, заполненного, горячіш ^ом^удеаіЕриво — дпть к уменьшению" частоты колебаний,, в то время как все гармоники должны были бы увеличивать свойственные им частоты. Объяснение этому легко усматривается пз диаграммы па рис. 48: хотя частоты каждой гармоники и уве-‘ личнпаются с возрастанием 1.2, по мере этого возрастания1 становятся пеустойчивыми все более и более низкие гар-| мопики, которые, рассеивая меньше энергии во виешпее: пространство, будут возбуждаться легче, чем высокие) гармоники, и смогут подавлять последние. Лишь прп очень j больших величинах когда оба конца трубы открыты,! появляется большая вероятность вторичного возбуждения! высоких гармоник. Вся совокупность имеющихся опытных! данных подтверждает этот вывод.
Полученные в пастоящем параграфе на основе формального анализа характеристического уравпения соотношения (28.6) имеют простой физический смысл. Если считать, что при известных условиях основной топ колебательной системы стал неустойчивым, т. е. к неустойчивости привела. например, пзвестпая комбинация величин р, v, Q* и Uj, то легко сообразить, что, в предположении неизменности процесса в зоне горения, точно такие же условия ((>, v, Q* и Ui) встретятся дважды на второй гармонике, трижды па третьей и т. д. Это связано с тем, что вторая гармоника как бы повторяет дважды стоячую волну колебаний основного тона, третья — трижды и т. д. Те же рассуждения справедливы и для моментов перехода от неустойчивости к устойчивости.
§ 29. Эксперименты по влиянию положения зоны горения на процесс колебаний
Целый ряд результатов, найденных в настоящей главе, подтверждается многочисленными экспериментами. Особенно поучительны в этом смысле’опыты. связанные с изучением влияния положения зоны горения по длпне трубы на процесс возбуждеппя акустических колебаппй. Некоторые из полученных при этом выводов могут иметь пе только теоретическое, по и практическое значение.
Прн оораоотке опытных данных целесообразно несколько упростить формулы (28.6). Поскольку все описываемые
Ниже опыты велись при сравнительно малых значениях Мг (порядка 0,05—0,1), то разности 1—М2 могут быть принятыми равными единице. Кроме того, формулы (28.6) целесообразно записать в размерных перемеппых (частоты в герцах, а длины в метрах), чтобы непосредственно сравнивать их с опытными точками. С учетом всех этнх замечании, соотношения, связывающие частоты колебаний и длипы холодной и горячей части течения, приобретают следующий вид:
![]()
Q
(29.1)
Здесь L и Ь2 — общая длина и длина горячей части течения, «j — скорость звука в холодной части течения, Q — частота колебаний в герцах. Q^1^ и Ь^ — частота колебаний па границе устойчивости и соответствующая длина горячей частя течения.
Получеппая формула исключительно проста и пе содержит величин, характеризующих детали процесса горения, численная оценка которых затруднительна. Все онп заключены в экспериментально определяемых значениях Q(1) п Z41). Остальные величины aly L, Ь.2 и Q) также измеряются совершенно просто.
В тех случаях, когда (как это часто бывает в эксперименте) наблюдается лишь одиа «лесенка» частот, например только области неустойчивости А0ВХ на рис. 47, формулы (29.1) допускают дальнейшее упрощение. Поскольку все точки Аа на рис. 47 получаются при N=0, а точки Вх прп N = 1, т. е. для постоянных N (которые полностью определены задаппем хотя бы одной точки А0 и 1?,), то формулы (29,1) можно записать в виде
![]()
(29.2)
Где QW и соответственно Ljj1* уже включают слагав’ Мы®, зависящие от /V. Пользование этими формулами край-
ие просто. Найдя экспериментально QO) и L^ для какой- либо точки А0, сразу получаем всю серию одноименных точек. Для построения серип точек надо подставить б выражения (20.2) QO> и L{i соответствующие какой-либо точке /?! и т. д. Если для таких расчетов будут браться ттаппизшие наблюдавшиеся частоты то числа К будут для всех других гармоник положительными.
Известным преимуществом формул (29.2) является, помпмо всего прочего, то, что опи не содержат такой величины, как п = —, измерение которой связано с некоторыми трудностями и данные по которой ие всегда приводятся экспериментаторами.
Ом
5 L,,m
Сравнение экспериментальных данных с теорией целесообразно начать с рассмотрения опытов Коварда, Харт — велла и Джорджсона, о которых уже говорилось в вводиой
S^, герц
— Теория Эксперимент
SO
Ом Z, 5
5 Lltm О
Рис. 49. Связь между положением фронта пламени и возбужден — вьімн частотами по опытам Коварда, Хартвелла н Джорджсона,
Главе. Опыты заключались в изучении вибрациопиого горения, возникавшего ири медленном распространении пламеии в трубе, закрытой с одпого конца, п заполненной горючей смссыо, при поджпганип смеси у открытого конца. В этих оиыта^х величина Ь. г равна расстоянию от открытого конца трубы до фронта пламени. Схема установки и результаты эксперимента приведены на рис. 49 и рис. 50.
Опыты ставились на двух трубах, несколько отличавшихся длиной и имевших разные диаметры (100 и 200 им?), поэтому па каждом из рисунков приведено по две диаграммы. Разница между рис. 49 и рис. 50 заключается в методике их получения. Теоретические области неустойчивости, приведенные па рнс. 49 (сплошные линии дают теоретически найденные области неустойчивости, а точки — экспериментальные даппые), были получены следующим образом. Из эксперимента бралось положение в плоскости
H-
I
>5,08м—
‘ 150
100 50
L, m5,0 W 3,0 2/1 10 0L*5.3 4,0 3,0 2,0 1,0 О
* I I I I I " і і і 1 1
О! 2 3 4м L, О I 2 3 4 SM L,
Рис.. 50. Связь между положением фронта пламени и иозбужден — иыми частотами по опытам Коварда, Хартвелла н Джорджсоиа.
Зкслерилгеш
(L2; Q) одной точки А, после чего с использованием формул (29.1) находились все другие точки, соответствующие границам устойчивости обоих типов. Эти точки соединялись прямыми, которые условно дают изменение Q в зависимости от L5 внутри области неустойчивости. Фактическое определение частот колебаний для точек, лежащих внутри области неустойчивости (т. е. таких, для которых v>0), не производилось, поэтому здесь говорится об условном характере изменения Q в зависимости от /v внутри области неустойчивости. На диаграмме не изображены области неустойчивости, теоретически существующие, но не наблюдавшиеся экспериментально. Все онн соответствуют более высоким частотам, чем изображенные на диа
грамме, и поэтому практического интереса но представляют. Вьппе уже говорилось, что возбуждение этих колебаний маловероятно.
На рис. 50 области неустойчивости построены также путем использования формул (29.1), но на этот раз только со знаком плюс. Для того чтобы компенсировать потерю половины границ устойчивости при таком расчете, в учет принималась не одна исходная точка А, а две (А и В), принадлежащие границам устойчивости противоположных типов. В остальном построение диаграмм иа рис. 50 ничем не отличалось от построения, описанного выше.
Сравнение теоретически найденных областей неустойчивости с наблюдавшимися экспериментально падо признать весьма удовлетворительным, особенно для тех областей, которые приведены на рис. 50. Единственным исключением являются точки, соответствующие Ь2, близким к пулю (т. е. положениям фронта пламени в непосредственной близости от закрытого конца трубы). Это связано с особенностями механизма самовозбуждения н будет объяснено в § 49.
Если сравнить между собою характер совпадения экспериментальных данных с теоретическими областями неустойчивости па рис. 49 и рис. 50, можно сделать следующий вывод. Лучшее совпадение теории с экспериментом. на рис. 50 связано с тем, что серия границ одного типа получена путем использования точки А, а серия границ противоположного типа путем использования точки В, в то время как на рис. 49 обо серии границ найдены с помощью точки А. Фпзнчески это означает, что характеры возмущенного процесса горения в момент наступления неустойчивости и в момент ее исчезновения не вполне одинаковы. Если бы опп совпадали, то зоны неустойчивости распределялись бы, как показало па рпс. 49, сплошными линиями. Причина этого различия станет понятной в § 49.
Более важиым, чем возможная разница свойств поверхности 2 в процессе перехода через грапицу устойчивости прп возиикновепші и прп исчезновении неустойчивости является хорошее совпадение теоретических и экспериментальных областей неустойчивости. Это говорит об одинаковом механизме возбуждения, действующем вне зависимости от номера гармоники, и удовлетворяющем условиям, выдвинутым в начале предыдущего параграфа. Там, в частности, делалось пред положение, что свойства поверхностп теплонодвода 2 не зависят от частоты. Это предположение включает, конечно, допущение об отсутствии запаздывания, так как введение времени запаздывания в тон илп иной форме прпвело бы, как показано выше, к зависимости свойств плоскости 2 от частоты [см., например, формулу (26.4)].
В рассматриваемом эксперименте происходило сгорание заранее подготовленной смеси газообразного горючего и воздуха, причем смесь сгорала в трубе, в которой пе располагалось никаких устройств для поддержания процесса горения (форсунки, стабилизаторы и т. п.). При таком характере горения в уравнениях, описывающих свойства поверхностп 2 (16.15), естественно положить (?*=0 и Рх = 0, т. е. считать, что возбуждеппе колебаний происходит только вследствие отличия от нуля возмущения эффективной скорости распространения пламени Uv Но тогда, по аналогии с формулой (24.2), можпо будет написать
U^U^+U plt (29.3)
Т. е. предположить зависимость Vх от возмущений давления п скорости. Коэффициенты ап, ан, аг1 п а23 в формулах (23.2) станут в этом случае линейными функциями £/„ и Up, и, следовательно, такими же свойствами будут обладать коэффициенты Сг, С2, С3 и С4 в выражениях (23.7).
Подставив в (23.7) для v=0 экспериментально найденное (например, для точки А) значение ш и значения hx и /г2, известные для той же точки А (поскольку они однозначно определяются заданием относительной длины горячей части трубы), можно рассматривать систему (23.7) как линейную неоднородную систему для определения Uv п U Фактическое вычисление Uv п Up позволит установить относительную амплитуду возмущепня эффективной скорости распространения пламени и ее фазу относительно возмущений vx и рх. Вычисления подобного рода могут дать полезные сведения о процессе, идущем о зоне горения, в момент наступления (или исчезновения) неустойчивости. Здесь эти расчеты пе приводятся, поскольку они пе имеют непосредственного отношения к содержанию настоящего параграфа.
Рассмотренные эксперименты были произведены в неподвижной смеси горючих газов, при свободном распространении в ней фронта пламени. Однако и при пзмеиеппи условий опыта найденные закономерности сохраняются. Обратимся с этой целыо к опытам, поставленным при сжигании заранее подготовленной смеси паров бензина с воздухом, движущейся по цилиндрической трубе. В указанных опытах была сделана попытка возбудить возможно большее число гармоник, чтобы наиболее полно сравнить теоретические зависимости с экспериментом. Это в известной мере удалось — если в он не а иной выше работе Коварда, Хартвелла и Джорджсоиа возбуждались три гармоники, то здесь было возбуждено семь гармоник.
Экспериментальная установка представляла собою открытую с двух концов трубу длиною в 4,57 м с диаметром в 100 мм. Эта труба свободпо обдувалась подогретым потоком бензо-воздущной смеси, которая непрерывно готовилась в специальном ресивере, отделенном от входного сечопия трубы свободным промежутком. Это было сделано для того, чтобы получить четкие краевые условия па обоих концах трубы: как входное, так и выходное ее сечения сообщались с окружающим пространством. Специально произведенными замерами было показано, что акустические колебания в трубе не передавались в ресивер, т. е. разрыв между выходным соплом, которым кончался ресивер, и входом в трубу был достаточно велик. Горение в трубе происходило за группой из нескольких стабилизаторов пламени (выполненных в виде конусов), расположенных в одной и той же плоскости, нормальной к осп трубы. Суммарная площадь проекции стабилизаторов на эту плоскость была мала по сравнению с площадью сечения трубы, т. е. стабилизаторы не загромождали с-ечепия, и акустические волпы свободпо проходили его, не испытывая заметных отражении от корпусов стабилизаторов.
Опыт заключался в том, что группа стабилизаторов, которая могла как целое перемещаться по трубе, постепенно сдвигалась по ней и через каждые 50 мм смещения производилась регистрация частоты колебаний.
![]()
V
&гери,
300-

1гмЮ № 7,0 OJ О
Рис. 51. Связь между положением стабилизатора иламеип ио длипе трубы и возбужденными частотами.
Результаты эксперимента приведены па рис. 51. Теоретические области неустойчивости построены по простейшим формулам (29.2) с использованием экспериментально найденных координат концов областей неустойчивости А и В. Взаимное расположение теоретических н экспериментальных областей неустойчивости вновь подтверждает справедливость соотношении, нолучепных в предыдущем параграфе. При этом следует особо подчеркнуть, что обе группы опытов, которые здесь рассматривались, были поставлены с различпымп краевыми условиями (закрытый п открытый конец трубы в одних опытах и два открытых копца в другпх), различным характером. движения газа (неподвижный относительно стенок газ в холодной части трубы и поток горючей смеси) и различной организацией горения (свободный фронт пламени и горение за плохо обтекаемыми стабилизаторами). Это указывает на большую универсальность полученных теоретических соотношений. Надо сказать, что это подтверждается также многими другими опытами, например ужо упоминавшимися экспериментальными исследованиями Путнэма и Депииса1) и других авторов.
Верпемсп к диаграмме па рис. 51 и рассмотрим ее с несколько иной точки зрения. Наряду с хорошим, для такого сложного явлення, совпадением теоретических п. экспериментально полученных областей неустойчивости, нетрудно заметить некоторое систематическое смещение их друг относительно друга. Это говорит о том, что свойства зоны тенлоподвода не вполне совпадают с теми, которые были постулированы в начале предыдущего параграфа. По-видимому, в рассматриваемом случае свойства зопы 2 в некоторой степени зависят от частоты колебаний, поскольку расхождение между теоретическими областями неустойчивости и экспериментальными точками систематически связано с измепеппем частоты колебаний. Этот результат надо признать естественным. В гл. VII будет показано, что при сжнгаппи заранее подготовленной смеси за плохо обтекаемыми стабилизаторами пламени механизм возбуждения п поддержания колебаний существенным образом связан с процессом •срыва вихрей со стабилизаторов. Из гидромеханики известно, что этот процесс может «подстраиваться» к частоте колебания скорости газа, обтекающего стабилизатор. Однако трудно предположить, что па этот процесс пе окажут влияния другие свойства вихре образования.
Л..’/LP у т„н 3 м 11, Д е е п и с,’ Исследоваипе вибрацноппого горения в горелках. Вопросы ракетной техники, № 5 (23), 1954.
Можно было бы тем же методом, на который было указано несколько выше, найти в этих опытах изменение Uv и Uv по мере изменения частот колебаний, и получить таким образом более глубокое представление о свойствах зоны теплоподвода. Однако такой анализ не входит в задачи настоящего параграфа.
Заметим, наконец, что на рис. 51 приведены лишь те области неустойчивости, которые соответствуют снижению частот колебаний по мере увеличения длины горячей части. В то же время из левой диаграммы рис. 48

Рис. 52. Осциллограмма колебания давления при внбращюлпом горении. Іірлмер од повременного возбуждения двух частот,
Следует, что при двух открытых концах трубы в процессе дальнейшего увеличения длины горячей части частоты колебаний должны вновь перескакивать на более высокие гармоники. Хотя в экспериментах подобное явдепие наблюдается сравнительно редко (так как при этом должна существовать короткая холодная и относительно длинная горячая часть точения), его удавалось зарегистрировать в установках, подобных той, которая использовалась для описанных здесь экспериментов.
Приведенные на рис. 48, 49, 50 и 51 области неустойчивости расположены таким образом, что прп некоторых относительных длинах горячен части течения становятся неустойчивыми сразу несколько гармоник. Это приводит к тому, что иногда возбуждаются сразу две, а то и три гармоники. Явление это наблюдается довольно часго и становится из рассмотрения упомянутых здесь диаграмм в полис понятным. На рис. 52 дан пример осциллограммы колебаний давления, снятой при вибрационном горении; на осциллограмме хорошо видно наложение двух гармоник — основной и имеющей вдвое большую частоту. Иногда осциллограммы приобретают еще более сложный вид и их расшифровка требует применения специальных методов. Одпако обычно основная частота может быть выделена сразу н нередко на сопутствующие ей частоты просто не обращают внимания.
Теория
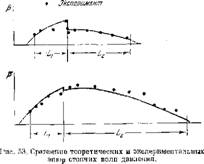
В конце предыдущего параграфа говорилось, что физической основой наблюдающегося скачкообразного изменения частот колебаний является способность колебательной системы как бы повторять форму стоячей волны дважды при возбуждении второй гармоники, трижды—третьей и т, д, С этой точки зрения совпадение теоретической картины скачкообразпого измепеипя частот колебаний с опытом косвеппо свидетельствует о том, что и формы стоячих волн близки к теоретическим. Этот факт можно зарегистрировать непосредственно, путем измерения формы стоячей волпы прп возбужденных в спстеме колебаниях. Проще всего это сделать для стоячей волпы давления. На рис. 53 приведены два примера сравнения
теоретических и экспериментальных эпюр абсолютных значений амплитуд стоячей волны давления. Как видно из диаграмм, опытные точки достаточпо хорошо следуют за теоретической зависимостью. Скачкообразное изменение теоретической эпюры в средней части диаграммы соответствует плоскости сильного разрыва X, которая представляет л идеализированном виде зону гореипя.
Если анализ процесса скачкообразного изменения частот колебаний при изменении длины горячей части трубы (п неизменной длипе трубы в целом) представляет скорее физический интерес, то реальпый практический иптерес имеет родственное явление, которое впешпе проявляется в известном смысле противоположным образом. Речь идет о свойстве колебательной системы стремиться к сохранению постоянного значения размерной частоты колебании при пепзмеппой длине горячей части и значительном увеличении общей длины трубы.
Пусть длила горячей части трубы Ьг остается постоянной, а общая ее длипа L непрерывно увеличивается. При этом относительная длина горячей части LJL будет уменьшаться, т. е. если вернуться к предыдущим диаграммам, движение будет идти не справа налево, а слева направо. Следовательно, та точка, которая соответствовала исчезновению неустойчивости, будет теперь соответствовать ее воз никп о велик» и наоборот.
![]()
(29.4)
Положим в утих формулах N=const, т. е. будем рассматривать родственные точки (паиримор, все левіле нлп все правые концы отрезков на рис. 51).
Пусть теперь, как уже говорилось выше, размерная длина горячен части течения будет постояіша (1/2=const). Тогда в правой части второго равепства (29.4) окажутся только постоянные величины. Следовательно, ло мере изменения общей длины трубы но при сохранении
В соответствии с формулами (29.1) можно написать
длины горячей части Ьг—const, колебательная система будет стремиться сохранить частоту колебаний Q неизменной при всяком новом возникновении неустойчивости.
Если обратиться теперь к первой формуле (29.4), то сразу видно, что это стремление колебательной системы может быть удовлетворено лишь за счет К, т. е. за счет перехода к возбуждению более высоких гармоник по мере увеличения общей длины трубы L.
Чтобы сделать эти выводы более наглядными, обратимся к примеру расчета. Найдем, пользуясь формулами
Я, г ер и
![]()
О 5 Ю ІЇ L, m
Рис. 54. Связь между возбуждаемыми частотами и длиноіі трубы при постоянной длине горячей части труби.
(29.4), прп N~ 1 моменты возникновения неустойчивости, а положив iV=0, сменив знаки прп на обратные п изменив абсолютную величину QW должным образом, моменты исчезновения неустойчивости. Результаты расчета построим в впде графика Q = Q (L), причем точкп начала и конца неустойчивости у словно соединим прямыми, чтобы отметить области неустойчивости. Соответствующее построение приведено на рпс. 54, причем около областей неустойчивости написано, каким К они соответствуют. Пример построен для численных значений параметров, совпадающих с теми, которые были характерны для эксперимента, представленного на рпс. 51. Прпведеппая па рпс. 54 диаграмма показывает, что в спстеме, независимо от длппы трубы L, можпо ожидать появлення колебаний только с частотами, л ежащими в пределах 61 —110 герц. 16 Б. В. Раутепбах
По мере увеличения общей длины трубы L частота коле — бапий в начале начинает снижаться, например, для области неустойчивости, соответствующей К = 1, со 110 герц до 61 герц, что вполне соответствует ожидаемому поведению системы, так как увеличение L увеличивает время пробега звукового импульса вдоль трубы.
Однако в дальнейшем не только не продолжается снижение Q, но, паоборот, частота скачкообразно повышается вновь до 110 герц, поскольку неустойчивой стала следующая гармоппка, соответствующая К-= 2. Прп этом
![]()
— 1-? д
![]()
Рис. 55. Энюры стоячих волн в трубах с одинаковой длиной горячей части течения.
D
І в
В некоторой области значений L могут одновременно существовать частоты порядка 105—110 герц и 61—72 герца для лежащих друг над другом участков К=2 и К=1.
Описанное явление наблюдалось в специальном эксперименте. Свободно обдуваемая воздушным потоком труба имела телескопическое устройство, которое позволяло непрерывно наращпвать длину входного участка, не изменяя режима обдува входного сечения. В концевой части трубы располагалась зона горения. После возбуждения вибрационного горения производилось медленное увеличение длины холодной части трубы и велось непрерывное наблюдение за изменением частот колебаний. Частоты колебаний первоначально имели тенденцию к снижению, но затем скачкообразно повышались до исходного значения.
Физические процессы, лежащие в основе явления, довольно просты. Пусть, например, существует некоторая труба с приблизительно одинаковыми длинами холодной и горячей части, и в ней возбуждены колебания основного тона. На рис. 55, А схематически показана эта труба н здесь же построена эпюра амплитуд колебаний давления в пей. Предположим, что возбуждепная частота и связанные с ней эпюры колебаний 6р и bv реализуют такие условия в зоне горенпя, которые в наибольшей мере способствуют возбуждению системы. Тогда, но мере увеличения общей длины трубы, сохранение процессов в зоне — горепия неизменными (в частности, сохранение н конфигураций эпюр амплитуд колебаний bp и bv) возможно только путем сохранения размерной частоты колебаний (на чертеже — расстояний между узлами на эпюре), т. е. перехода к более высоким гармоникам. В нижней части рис. 55 приведена соответствующая схема трубы с удлиненной холодной частью.
Таким образом, возбуждаемая системой частота колебаний в известном смысле определяется длиною и свойствами горячей части трубы, т. е. камеры сгорания. Сделанный вывод согласуется со всем имеющимся экспериментальным материалом.
Надо заметить, что этот вывод имеет большое практическое значение. Дело в том, что нри исследовании камер сгорания возникает вопрос о возможности испытаний их изолированно от двигателя, путем присоединения к воздухопроводу, нередко имеющему очень большую длину. Казалось бы, при этом нарушается всякое подобие акустических условий работы и поэтому изучать на такой установке процессы вибрационного горения испытываемой камеры псльзя. Однако анализ явления, который был проведен выше, показывает, что это простое рассуждение является неточным и если камера сгорания склонна к неустойчивости (вибрационному горению), то эта неустойчивость проявится (причем в тех же формах, без изменения частоты колебаппй п т. п.) п па установке с длинным входным воздухопроводом.
Полученный результат не следует истолковывать в том смысле, что колебательная система вообще нечувствительна к изменению длины холодной части трубы. По сути, здесь было показано только то, что если вместо некоторой длины холодной части трубы Ьх взять другую, L*, то При условии, что новая длина будет во много раз больше исходной {Ll >L1)> процесс колебаний будет характеризоваться стремлением к сохранению как частоты, так и всех
1С*
Иных своих свойств. Это позволяет вести испытания камер сгорания на стендах, характеризующихся очень длинными воздухоподводящими трубопроводами, не слишком рискуя шість акустические условии в зоне горения, резко отличные от натурных. Однако пз отого вовсе не следует, что при изменении длины все свойства колебательной системы сохранятся. Чтобы показать это, рассмотрим такой пример. Пусть область неустойчивости мала и в нормальных условиях система не возбуждается.
Р

0 / 2 ~ 3 4 5
Рис, 5’і. Влияние длины трубы на устойчивость течения.
Начнем увеличивать длину холодиой части трубы Lx сохраняя все размеры горячей части постоянными. Тогда диаграмма распределения областей устойчивости, аналогичная приведенной на рис. 54, может иметь впд, показанный на рис. 56. Пусть исходная полная длина трубы будет, например, X=2,5 м (линия АА на рис. 56). Это соответствует отсутствию колебаиий, поскольку линия АА пе пересекает областей неустойчивости (изображенных на диаграмме сплошными линиями). Удлиним теперь входной участок трубы, сохраняя размеры зоиы горения и участка трубы, по которому текут продукты сгорания, неизменными. При £/>3,1 м любая длина L будет соответствовать какой-либо области неустойчивости (линия В В на рис. 56), т. е. при достаточпо большом удлинении входного участка трубы, первоначально стабильный процесс может стать неустойчивым. Правда, это предполагает, что система в целом склонна к возбуждению, т. е. обладает областями неустойчивости. Таким образом, если система способна возбудиться, то эта способность особенно легко реализуется по мере удлинения входного участка точеппя.
Этот результат тоже представляет значительный практический интерес. Он говорит, что если камера сгорания доведена на стенде с длинным трубопроводом и не дает па нем внбрационных режимов горения, то возникновение их прп переходе к более коротким входным участкам маловероятно. И в то же время, если камера сгорания доведена прп малой длине входного участка, то простое удлинение его способно привести к влбрацпонному горению.
Сказанное можно подтвердить следующим экспериментом. Для опытов была использована камера сгорания со входным участком течения, имевшим длину 700 мм. Изменяя подачу горючего, удавалось получать коэффициенты избытка воздуха от а = 1 до а=3. Во время опыта регистрировались амплитуды колебаний давлення перед зоной горения Ьр. Эти амплитуды относились к избыточному (по отношению ко в пешней среде) давлению полностью заторможенного потока воздуха перед камерой сгорания <j. Относительные величины возмущении
Давления ~ строились в фупкцпи коэффициента избытка воздуха а. На нормальных, «спокойных» режимах горенпя ^ пе превышало величин порядка 0,1—0,15. На рпс. 57 даны экспериментально полученные зависимости ^ = /(а)для трех случаев: кривая а соответствует исходному варианту установки, с длиной входного участка Јj=700 мм-, кривая с — длине входного участка 1400 мм кривая г — длине входного участка 2800 мм. Как видно пз эксперимента, нервоначально стабильпый процесс сгорания становился вибрационным (с увеличением амплитуд колебаппй в 5—10 раз) от одного только увеличения дл пныхолоднон части течения L,, как это и следует из развитой теории.
Надо, правда, добавить, что рассуждения, на основе которых оылн получепы приведенные выше выводы, исходили пз предположения, что все области пеустой — чивости характеризуются совершенно одинаковыми механизмами возбуждения и гашения колебании. Это, конечно, не всегда имеет место, особенно если колебательная система способна возбудиться при помощи разных физических процессов, реализующих обратную связь (подробнее о них см. гл. VII). Все же подтверждение многих
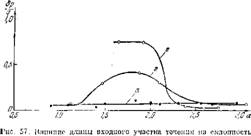
Системы к возбуждению.
Следствий из развитой простейшей теории указывает на то, что ею можно пользоваться как теорией первого приближения.
В заключение настоящего параграфа полезно привести некоторые дополнительные данные по акустике стендовых установок, не относящиеся непосредственно к вопросу о влиянии отноептельпых длин горячей и холодной частей течения на области неустойчив ости.
Хотя испытания камеры сгорания на длинном подводящем воздухопроводе дают известную гарантию того, что прп переходе к более коротким входным участкам склонность колебательной системы к возбуждению скорее уменьшится, чем увеличится, иногда может представить интерес пепытаппе камеры сгорания с коротким входным участком, па который не влияет подводящий воздухопровод. В этом случае мыслимы две схемы, которые акустически разделяют входной участок камеры сгорания и стендовый воздухопровод (рпс. 58).
Первая пз этих двух схем сводится к созданию ресивера перед входным сечением канала, ведущего к камере сгорания, а вторая — к разрыву трубопровода в пужпом месте (опа нрнмепнма лишь прп ограниченных давлениях внутри трубопровода).
Рассмотрим первую из названных схем. Интуитивно ясно, что если ссченпе ресивера S2 будет много больше, чем сечение трубы Sv то ресивер фактически станет своеобразной «внешней средой», а в месте стыка образуется узел давления. Труба с камерой сгорания будет как бы отделена от всех подводящих воздух магистралей. Обьгчпо сечение S2 не может быть сделано очень большим п поэтому представляет интерес численная оценка влияния отношения S^ISi на степепь приближения условия па стыке труб разных диаметров к узлу давления.
В книге Апдреева и Русакова1) приводится такое выражение для отношения амплитуды, прошедшей через стык труб волпы давлення, к амплитуде подошедшей волны:
2
= Г" •
Очевидно, что коэффициент 1] характеризует степень приближения рассматриваемого изменения сечения к полностью открытому концу. Прп этом г|=0 указывает на отсут — ствие проходящей волны (полное отражение), а г)=1 на то,
ST.
Рис. 58. Две схемы разделения стендового воздухопровода и входного участка камеры сгорания.
Д Р е ^mJ1- 11 ■ 11 р У с а к о в И. Г., Акустпка движущейся среды. ГТТИ, 1934.

Дюс=ЯЮ.
Величина c/nami/vet/cp — го іїавлені/я, замеренная /7р&є£/жн6/м ш/77-
W/гом в указанных тач/гах {колебательная сое/павля/ащая]
![]()
<П
Рік.’. 59. Эпюры амплитуд колебания давления на стыке ресивера и начального участка трубы камеры сгорапия.
Метрами 150, 300, 400 и 500 мм. По длине ресивера и трубы в окрестностях их стыка производилось измерение амплитуд колебания давления. Соответствующие эпюры и общая схема установки даиы на рис. 59.
Из приведенных графиков видно, что по мере увеличения отпошеппя SJSx условия па степке труб все более приближаются к условиям, характерным для открытого конца. Даже такое небольшое увеличение диаметра прп переходе к ресиверу, как переход от 100 мм к 150 мм, дает четкую эпюру стоячей волны в трубе. С увеличе-
Что волпа полностью проходит. Таким образом, уменьшение ї) означает приближение к условию открытого конца. В специально поставленном эксперименте цилиндрическая труба диаметром 100 мм, в которой происходило вибрационное горение, подсоединялась к ресиверам с диа-
|
F^lF- |
|
|
ХслсЗная час/пь |
11 і камера |
|
Труды |
Сесраная |
|
Груба камеръ/ сеараная |
Точки зпмара статического давления
-Н
Пнем S., амплитуды колебании в ресивере, как и следовало ожидать, уменьшаются. По-видимому, достаточно полное разделение ресивера и трубы получается при 5а/51>3.
ТИ-
"Г
Вторая схема также изучалась экспериментально. Разрыв трубопровода имел ту же цель — сформировать колебания с узлом давления в месте разрыва. Схема
Подводящий тофпровоЗ, Тачки стигло чесШо ggj^ / Заметя
|
_Г J |
|
|
Л’олоЗтя vae/m трубы |
Комора |
|
Сгорания Труба кямедд/ егарания |

Рис. 60. Эпюры амплитуд колебаппй давления в окрестпос-ш разрыва трубопровода.
Опытной установки и распределение амплитуд колеианпп при вибрационном горении, измеренных в окрестности разрыва, даны на рис. 60. Так же, как и в предыдущих опытах, в трубе диаметром 100 мм возбуждалось вибрационное горение. При разрыве Д£=10 мм колебания передавались через разрыв так, будто оп не существует. При этом частота колебаний (110 герц) оказалась в полном соответствии с суммарной длиной обеих частей трубы,
разделенных разрывом. При разрывах в 20 мм и J00 мм картина резко менялась. Эпюра колебаний давления явно стремилась к нулю в месте разрыва, а в левой части трубы наблюдались колебания постоянной, но малой амплитуды. Прп этом частота колебании повысилась до 130 герц и стала соответствовать длине правой части трубы, без участка, лежащего по другую сторону разрыва. Это говорит о том, что для получения должного эффекта разрыв между трубами должен быть порядка 20% от диаметра труб или больше.
Можпо, конечно, комбинировать обе приведенные схемы, делая подводящую трубу большего диаметра, чем труба, в которой происходит гореппе, и одновременно сохраняя разрыв.
Полученный экспериментальный результат хороню согласуется с опытами Коварда, Хартвелла и Джордж — сопа, описанными в § 1. Приближение в указанных опытах пластины к открытому концу трубы (диаметр ее был тоже 100 мм) практически не сказывалось иа характере колебаний при расстояниях между пластиной и трубой, равных 60 мм и 30 мм. Прп расстояниях 15 мм и меньше характер вибрационного горения изменялся весьма резко (см. рис. 1). Таким образом, и здесь удаление пластины на расстояние, превышающее 20% диаметра, практически разрывало связь между колебаниями газа в трубе и подводимым к устью трубы препятствием.



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике