Если рассмотренные в предыдущих параграфах процессы вибрационного горения были в той или иной степени связаны с подвижностью фронта пламени, то классическим примером системы, в которой подвижность поверхности теплопровода совершенно исключена, является труба Рпйке. Кроме того, устанавливаемая в такой трубе сетка настолько топка, что можно пренебрегать ее протяженностью в направлении осп трубы и поэтому полагать объем V в уравнениях (15.5) равным пулю, Это приводит к тому, что исключается и иоявлепие подвижности некоторого эффективного фропта пламени, который иногда полезно вводить пз формальных соображений.
Следовательно, труба Рийке является наиболее ярким примером возбуждения акустических колебаний тепло — подводом. Это обстоятельство делает целесообразным рассмотрение процесса возбуждения звука в такой трубе, хотя оно и не связапо с каким-либо процессом горения.
Как уже говорилось, труба Рийке представляет собою вертикально установленную трубу, в которой осуществляется слабый проток воздуха. Обычно этот проток связан с тем, что установленная в одпом из сечений трубы нагретая сетка несколько подогревает вышележащие слои и создает таким образом тягу. Центральным прп анализе возбуждения звука трубой Рийке является вопрос о передаче тепла от нагрЬтой сетки к пересекающему ее воздуху и связи этой теплоотдачи с акустическими колебаниями. Основываясь па результатах, полу- чеипых в предыдущих главах, пе представляет труда провести апализ этих вопросов.
Рассмотрим свойства поверхности теплоподвода 2. В описываемом случае пагретая сетка и вводимая чисто формально плоскость теплоподвода 2 будут совпадать. Это, пожалуй, единственный случай, когда плоскость теплоподвода 2 имеет такой четкий физический смысл. Поскольку в обычном режиме сотка может нагреть пересекающий ее воздух лишь незначительно, будем считать, что МХ=М2, п=1 и поэтому уравнения связи параметров колебаний слева и справа от 2 примут в простейшем случае вид (20.3):
І
J (48.1)
Следует обратить внимание на то, что единственным параметром, от которого может зависеть самовозбуждение системы, является безразмерное возмущение теплоподвода Q, которое можно [иа основании формул (15.8) и (20.2)] записать в форме
Q = (48.2)
Рассмотрим более подробно возмущение теплоподвода bQ*. Будем считать, что проволочки, составляющие нагретую сетку, достаточно тонки, В этом случае для расчета секупдпои теплоотдачи от сеткп к воздуху можно воспользоваться одной из известных формул, например формулой Кинга1):
Q*=±a(Tu-T)l, j
, , ‘ (48.3)
Где X — теплопроводность воздуха, D —- диаметр проволочки, I _ ее полная длила, Тп — температура проволочки, Т — температура среды.
^ " 0 л • Измерение воздушных потоков, Госте!’-
Издат, 1947,
Множитель ~ введен в первую пз наннсаниых формул для приведения секундного потока тепла к единице площади сечения трубы.
Еслп частота колебаний мала, то, как это видно из второй формулы (48.Я), возмущение (?*, т. е. изменение 6Q*, будет происходить в фазе с изменением скорости течения 6 с1:
6Q* = r,(Tn~T) (48.4)
При больших частотах колебаний картина резко изменяется. Процессы в пограничном слое становятся существенно нестациона рпымп, нестацпопа рной становится вследствие этого и теплоотдача. Теоретический анализ этого явления, как, впрочем, и экспериментальное его изучение представляют огромные трудности. Сравнительно недавно Лайтхиллом было получено приближенное теоретическое решеппо подобной задачи для ламинарного обтекания бесконечно длинной проволоки, обдуваемой потоком газа, направленного нормально к ней, скорость течения которого имеет малую синусоидальную составляющую1). Полученный им результат сводится вкратце к следующему: если частота колебаний весьма велика, то независимо от этой частоты фаза возмущения теплоотдачи начпнает отставать от фазы возмущения скорости на угол. Амплитуда возмущения теплоотдачи монотонно убывает с увеличением частоты колебаний, На рнс. 95 представлен график, заимствованный из указанной работы, на котором приведены две кривые, Одна нз них дает величину г|з — фазового запаздывания 6Q* отпосптельпо стационарного 6Q*.т (6(2*, которое было бы прп бесконечно малой частоте колебаний),
А вторая — отпошеппе амплптуд у^гу» равное т]. Обе
V СТ 2лй D
Кривые построены в функции параметра —-—, где
L і g k t її і 11 M. I., Tlie response of laminar skin friction and heat transfer to fluctuations in the slre&m velocity. Proceedings of the Royal Society, Ser. A, vol. 224, № 1156, 1954.
Q — частота акустических колебаний в герцах, a D — диаметр про во л очі» и. Приведенные кривые показывают, что ослабление возмущения теплоподвода rj прп достаточно больших Q может быть весьма значительным, а фазовое запаздывание нарастает с частотой достаточпо быстро и практически достигает предельного значения, равного -2- , в момент, когда ослабление амилитуды возмущения теплоподвода имеет порядок 0,15. Если оцепить порядок
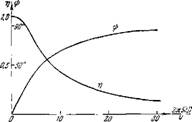
Рис. 95. Ослабление амплитуды г п фазовое запаз — дываппо і]’ при передаче тепла от проволочки к течей ню воздуха, имеющему гаумоипческую составляющую.
2.-Т QZ)
Величины параметра —-— , который может наолюдаться в трубе Рийке, то для D = 1 мм, Q = 500 герц и и = 0,1 м/сек получим его блпзкпм к 30. Это указывает, что в трубе Рийке можпо ожидать существенного ослабления амплитуды возмущения теплоподвода (приблизительно в 10 раз по сравнению с соответствующей величиной для квазистационарного процесса) и предельного фазового запаздывания, равиого ~ .
Если ослабление амплитуды возмущения теплоподвода имеет только количественное влияние на процесс возбуждения звука в трубе Рийке, то фазовое запаздывание является важнепгапм фактором в рассматриваемом явлении. Легко убедиться, что при отсутствии фазового запаздывания звук в трубе Рийке не возбуждался бы никогда. Действительно, еслп бы фаза Q и фаза v} совпадали [формула (48.4)1, то на основании формул (17.1) и (48.1)
= v vі
Г{і м ‘ _ ! (48.5)
ЬЕ имело бы также фазу, совпадающую с фазой у,, а ЬХ — противоположную фазу. Предполагая отсутствие потерь во внешнюю среду, можно было бы написать условие возбуждения акустических колебаний в виде неравенства
Js > 0. *
Б то же время по формуле (19.2)
= Y (р, ЬЕ + 6Х + б Е ЬХ).
Поскольку внешние потерп отсутствуют, Pi _L а следовательно, первое из трех слагаемых As равно нулю, а два других — отрицательны {ЬХ находится в противо — фазе с п ЬЕ). Следовательно, А^ < 0, п возбуждение звука невозможно. Таким образом, запаздывание фазы возмущения скорости ивляотсн необходимым условием самовозбуждения акустических колебаний в трубе Рийке.
Не следует думать, что использование теоретических кривых Лайтхилла всегда дает предельное фазовое запаздывание, равное у — . Приведенный выше численный пример соответствовал в некотором смысле крайнему случаю. Более реальным случаем будет возбуждение звука в длинной трубе Рийке прп помощи сетки, состоящей из сравнительно тонких проволочек. Еслп положить Q = =100 герц; Л=0,3 мм; і> = 0,3 м>сек, то т. е. фазовое запаздывание ty будет порядка нескольких градусов, а ослабление амплитуды возмущения тепло — подвода практически будет отсутствовать вовсе (ri^l). Таким образом, можпо ожидать, что в трубе Рийке будет иметь место весьма широкий диапазон изменений пара — 2nQD
Метра —-— и связанных с ннм явлении.
Здесь уместно подчеркнуть, что использование теоретических результатов Лайтхилла для расчета самовозбуждения звука в трубе Рийке вряд ли возможно признать, без дальнейшего исследования этого вопроса, законной операцией.
Составляющие сетку проволочки работают в совершенно иных условиях, чем те, которые полбжил в основу своего расчета Лайтхилл. Оп рассматривал одиночную проволоку в бесконечном пространстве, в то время как в сотке расстояния между проволочками имеют порядок их диаметра, и взаимное влияние соседних проволочек безусловно значительно. Кроме того, Лайтхилл считал, что синусоидальная составляющая скорости течения мала по сравнению с его средней скоростью, в то время как опыты Лема на1) показали, что фактически в трубе Рийке амплитуда колебания скорости в 2—6 раз превосходит среднюю скорость течения. Совершенно ясно, что такое изменение условий обтекания проволоки должно существенно изменить кривые на рпс. 95.
Опыты Лемана косвенно подтверждают высказанное здесь предположение. Если бы кривые Лайтхилла можно было непосредственно прилагать к сеткам в трубе Рийке, то изменение диаметра проволочек в сильной степени влияло бы на самовозбуждение звука. Однако упомянутые опыты показывают, что подобное влияние практически отсутствует.
В настоящее время пет данных по пестационарпой теплоотдаче от нагретых сеток, поэтому количественный анализ звучання трубы Рийке фактически невозможен. Чтобы дать качественное представление об этом явлении, можно воспользоваться кривой Лайтхилла, которая дает возможность учитывать наиболее существенный фактор — наличие фазового запаздывания между возмущением теплоподвода и возлгущением скорости.
Прежде чем приступать к численпому анализу возбуждения звука в трубе Рийке, пеобходимо уточнить формулы первого приближения (48.1), которые использовались до сих пор в качестве соотношений, описывающих процесс на поверхности теплоподвода 2. В эти соотношения необходимо внести уточнения. Во-первых, можно было бы уточнить их, учтя, что температура воздуха, прошедшего через сетку, выше температуры воздуха, подходящего к сетке. В уже упоминавшихся опытах Лемана было показано, что на нормальных режимах воздух после сетки пагревается на 100—150D, т. е. сравнительно мало. Поэтому учет нагрева (т. е. учет того, что Мг Ф М2 п Ф 1) не сможет заметно сказаться на результатах анализа.
(48 .(>)
Более существенным является учет гидравлического сопротивления сетки. При рассмотрении процесса горения в тоиках или камерах сгорания обычно можно пренебрегать гидравлическими потерями, так как они невелики. При описании возбуждения звука в трубе Рийке всегда указывается, что сетка должна быть густой, а это влечет за собою заметные гидравлические сопротивления. Полученные в гл. IV общие уравнения позволяют учитывать и этот фактор. Если исходить из системы уравнений (20.1) и учесть, что все члены, связанные с возмущением теплоподвода, кроме Q = 2MQ*, равны нулю, можно получить вместо соотношений (48.1) следующие равенства:
— к—1 тг кМ3 — р
V* — Vl + 2(1 — ЛЯ) " ~~ i-M* I
7 -» м О I (*-1)А/4+л*а;р
P-i-lh М 2(t-M*) V+ )
2(1 —м*) V ^ 1-А/2
(48.7)
Соответственно вместо равенств (48.5) надо будет напясать:
6 f — л 1 о ti р
— 2(1—Д/ч * 1-АЯ
Ьх= — м у—1
Ил 2(1-АЯ) V-t — х
Величину Рх легко связать с коэффициентом гидравлического сопротивления если считать, что в этом
случае применима гипотеза стационарности. Действительно, обозначив потери давления па сетке рг> запишем обычное гидравлическое равенство
У 6£’2
Возмущение этой величины будет равно бPl^lqv 6i»r
Величина Рх=г — 6р^ будет характеризовать спловое воздействие сетки на поток. Переход к безразмерным переменным (15.8) дает
-Іг"’- <[12]-8)
Величину Q определим, исходя из равенств (48.2) п (48.3). Предположим, что входящий в выражение для а (48.3) корень заметно больше единицы1):
/
(48.9)
Тогда можпо написать, что
Q* = Л Tv,
Где Л —некоторая постоянная. Соответственно
Или
= (48.10)
Воспользовавшись фо|імулой (48.2), запишем:
^ISr5» (/і8л1)
Где Q* соответствует теплоподводу от сетки ГфН отсутствии возмущений течения.
Формулы (48.7), (48.8) и (48.11) полностью определяют процесс на поверхностп разрыва 2, если считать, что известен теплоподвод Q*, коэффициент гидравлического сопротивления сетки £ п параметры г] и характеризующие отклонения от стационарности процесса теплоотдачи от сетки к воздуху.
Располагая всеми указанными данными, можпо было бы решить соответствующую краевую задачу, подобно тому, как это делалось в гл. У, VI и других местах. Однако достаточно полное представление о возбуждении звука и трубе Рийке более просто получить путем использования. энергетического метода, развитого в гл. III и IV. В рассматриваемом случае применение энергетического метода напрашивается потому, что частоты возбуждаемых колебаний можно считать известными. Все исследователи, паблюдавшпе звучание трубы Рийке, всегда указывают, что возбуждаются колебания с частотами, определяемыми обычнымп акустическими соотношениями (т. е. ие требующими для своего определения учета постоянной составляющей скорости течения вдоль трубы и учета свойств зоны теплоподвода). Поскольку единственный важный параметр колебаний — частота,— определение которого из энергетических соображений невозможно, известеп, использование энергетического метода является совершенно естественным.
В качестве типичных численных данных используем те, которые были реализованы в опытах «Немана. Это позволит сопоставить результаты расчета с экспериментом. В названных опытах основная масса эксперт! ентов была проведена на трубе, имевшей диаметр d—61 мм и общую длину L = 1140 мм. В трубе обычно возбуждались колебания осповного топа (частота 165 гц) и иногда второй гармоники (частота 330 гц). Скорость течения в трубе изменялась по желанию экспериментатора, так как она создавалась не тягой, а вентилятором, питавшим воздухом большой ресивер, к которому присоединялась труба. Располагавшаяся в некотором сечении трубы тонкая проволока (диаметр 0,2 мм, шаг 2 мм) нагревалась электрическим током. В непосредственной близости от нее помещалась частая металлическая сетка,. которая воспринимала тепло от раскаленной проволоки и передавала его воздуху. Как уже указывалось, сама раскаленная проволока (без частой сетки) звука возбудить ие могла. Диаметр проволочек, пз которых составлялась частая сетка, оказывал лишь незначительное влияние на процесс возбуждения звука (в опытах Лема па количество ячеек на 1 см’1 менялось от 1115 до 46,8, что, по-видимому, соответствует изменению диаметров проволочек, составлявших сетку от 0,1 мм до 0,5 мм). Средняя скорость течения по трубе изменялась от 0 до 0,7 м/сек. Наиболее сильное звучапие получалось при скоростях 0,3 — 0,45 м/сек. Количество тепла, которое передавалось от сетки к воздуху, изменялось от 272 до 480 ватт.
Примем для расчета некоторые средние значения параметров, характерные для опытов Лемана. Пусть скорость течения у=0,35 м/сек, средний теплоподвод і^*=432 ватта, средняя скорость звука в трубе равна 376 м./сек (она определена пз наблюдавшихся частот колебаний), а диаметр проволочек, из которых составлена сетка, 0 = 0,35 мм. Для основного тона (Q = 165 горц) это
2л ШЗ, л
Даст —-—^ ‘1 и соответственно г) ^ 1 и запаздывание
Хотя последние величины получены на основе срафика Лайтхилла (рис. 95), допустимость применения которого вызывает законное недоверие, здесь они будут взяты в качестве некоторых параметров первого приближения, имеющих, вероятно, правильные порядки величин, тем более, что другие данные в настоящее время отсутствуют. Главное, что здесь вводится, — это некоторое запаздывание возмущения теплоподвода Q относительно возмущения скорости V.
Воспользуемся теперь известным энергетическим условием (19.3), справедливым для границы устойчивости
= 0. (48.12)
Вычислим обе входящие в написанное равенство величины. Как уже упоминалось в настоящем параграфе,
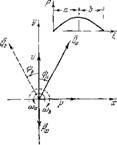
Рис. 96. Фазовое смещение вектора Q вследствие запаздывания в зависимости от положения сечения теплоподвода относительно стоячей волны колебаний давления.
42$ Частные случаи самовозбуж,1енпн [гл. x
Определим фазовые сдвиги между векторами, входящими в написанное равенство. Предварительно рассмотрим положение векторов на рис. 90. Векторы р и и направлены как обычно — первый в положительную сторону осп х, а второй — осп у (здесь предполагается малость Н). Вектор как это следует из равенства (48.8), всегда направлен в сторону, противоположную вектору v. Вектор Q нри очень малых частотах имеет ту же фазу, что п V, а вообще его фаза сдвинута относительно vL на угол в результате запаздывания. Чтобы определить, в какую сторону от оси у откладывать угол ф, для нахождения фаз Q следует учесть направление вращения всей диаграммы векторов с угловой скоростью ш. Легко сообразить, что это направление будет различным для разных участков стоячей волны давления. В верхней части рнс. Обдана схема стоячей волны колебаний давлення, охватывающая половин}’- полной длины волны. Изображаемая на этой схеме полуволна разбпта на участки а и b, лежащие по разные стороны пучности давления. На участке а при переходе через максимум давления возмущение скорости течения изменяет знак — из положительного (направленного к пучности давлеиия) оно становится отрицательным. Это происходит потому, что прп постепенном сжатии газа массами, движущимися к пучности давлення, давление возрастает, достигает максимума, после чего колебательная составляющая скорости течения изменяет знак, так как газ приобретает составляющую движения влево, в сторону
пониженных давлений. Точно такой же процесс на участке Ь приводит к тому, что при переходе возмущения давления через максимум колебательная составляющая скорости течения, изменяя знак, превращается пз отрицательной в положительную. Поэтому па векторной диаграмме. приведенной на рис. 96, направление ю для участков а и b будет различным: для участка а — против часовой стрелки, для участка b — по часовой стрелке. Вообще при принятых направлениях отсчета участки стоячей волны, лежащие между узлом и пучностью давления и расположенные влево от пучности давления, будут характеризоваться направлением угловой скорости соа, а остальные участки — угловой скоростью cof;. Поскольку фазовый сдвиг ф обусловлен запаздыванием, постольку и положение вектора Q будет различным: Q для участков а будет сдвинуто на угол ф вправо от для участков b — влево.
Рассмотрим тепорь выражеппе для
Воспользовавшись равенствами (48.7) и пренебрегая малым слагаемым и велИ1Шной М’1 по сравпе-
Нию с Мй, можно для участков а написать:
+м 2ЇГЗЖЇ) I 11QIcos (180° + ^ —
Для участков b Л» будет выражаться точно так же, за исключением того, что знаки перед ф надо будет измелить на обратные.
Упростим написанное выражение, полагая 1—М2=1, —-)— = 0,2, а угол ф—малым по абсолютному значению.
![]()
Тогда для участков а
^410,21^1 vl{Q-
—M*Px\vx~$№MQ*-02M*Q\Px\. (48.13)
Как следует из паштсанпого равенства, при малых но абсолютному значению ф все слагаемые, кроме первого, дают отрицательные величины, т. е. гасят колебания. Лишь первое слагаемое может быть положительным при ф > 0, что возможно лпшь для участков а. Для участков Ъ ф < 0 п, как это следует пз наппсаппой формулы, возбуждение невозможно. Этот результат можно было ожидать, так как выше неоднократно указывалось, что прп положении вектора возмущеппого теплоподвода во второй четверти возбуждение невозможно (см., например, диаграммы устойчивости рпс. 29).
Подставим в соотношение (48.13) найденные несколько выше значения Q и Рх. Для выбранных численных величин
I (48.14)
Где v следует брать в м/сек. Чтобы определить величину Рх, зададим £ = 5, что приблизительно соответствует (при малых числах Рсйнольдса) проволочной сетке с отношением живого сечения к сечению трубы порядка 0,4 —0,5 [13]). Производя необходимые вычисления, получим следующие выражения:
At=0,021 иг |рг j — 0,0035 ] |[14] для участка а,
^ = -0,021^11^1-0,00351^ для участка Ь.
Изменение v1 и [ рх | в зависимости от положения сетки по длипе трубы можно нринять
I vt I = с COS ф (,| Pi | = с I Sin ф | (с > 0), где ф = /ся£, как это следует из формул (6.3).
Л,
График изменения и функции параметра ср приведен па рис. 97. Как видно из графика, положительные зиачепия Де простираются от ср = 10° до ср = 90°. Равенство (48.12) позволяет учесть потери эпергпи, связанные с излучением ее из открытых концов трубы. При наличии потерь на излучение векторы и [v^ перестают
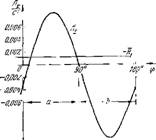
Рис. 97. Поток акустической энергии в зависимости от положения плоскости теплоподвода по длипе трубы.
Быть взапмпо перпендикулярными и поэтому формула (48.13) должна была бы включать дополнительный поворот їїг отноептельно pv но поскольку для малых потерь этот поворот тоже будет мал, здесь соответствующей уточпение вводиться пе будет, и выражение даваемое формулами (48.15), будет считаться правильным.
При заданных d и L концевой имиедапц трубы (30.8) будет равен
Z — 0,000216со2 -f 0,0187(О(,
Причем безразмерная частота колебаний со для первой гармоники равна со = jt, а дли второй со = 2л.
Воспользовавшись найденным зиачепием z, определим потери па пзлучеппе из обоих концов трубы. Это ножно сделать путем удвоения потока акустической энергии из одного коицевого сечения
R = р v.
ГГри этом следует учесть, что v ^ с, а величина р и угол между р и v легко находятся из равенства
Р — ZV.
Вьгчислеиия дают для первой гармоники ~ = 0,0014,
С2 ‘
А для второй
-0,005В.
С2 ‘
£
Прямая нанесена на график рис. 97. Она позволяет выделить область неустойчивости, соответствующую As — Ri > 0, которая простирается от ф ^ 14° до ф 87°. Совершенно аналогичное построение можпо привести и для второй гармоники. Если при этом учесть, что вслед — 2я QD
Ствпе увеличения параметра —-— вдвое примерно во стол],ко же раз увеличивается и запаздывание, а потери Яи
— =0,0056, то область неустойчивости оказывается расположенной от ф = 13° до ф—83°.
Воспользовавшись уже приводившимся соотношением ф=/»:я|(А.’=1 для первой гармоникк и к.= 2 для второй), построим области неустойчивости для двух первых гармоник в фупкции относительного положения сетки по длине трубы (рис. 98). Приведенная диаграмма хорошо согласуется с опытными данными. Во-первых, видно, что основпоп тон трубы может быть возбужден лишь в том случае, если координата £<0,5, т. е. если сетка находится в нижней части трубы. Более того, если вернуться к рис. 97, то сразу видно, что наибольшего зпачения раз-
НОСТЬ — І2 — Я достигает приблизительно при,
Т. е. при £ = 0,25. Это полностью согласуется с указаниями экспериментаторов, что наиболее сильное звучание имеет место в том случае, если нагретая сетка располагается на расстоянии, равном 1/4 общей длины трубы,
Я, г ери
J30
О 0,5 10 і
Рис. 98. Распределение областей неустойчивости по длине трубы для двух первых гармоник.
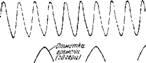
Считая от нижнего конца. При £<0,25 становится неустойчивой и вторая гармоппка. В опытах Лемана это обстоятельство было зарегистрировано в виде наложения колебаний двух гармоник при £<0,25, причем по мере уменьшения | вторая гармопика начинала пграть все более заметную роль. Соответствующие осциллограммы приведены на рис. 99.
Анализ построенных диаграмм объясняет и то, почему в опытах Босша и Рпсса звучание возбуждалось только в том случае, если |>0,5, т. е. при положении сетки в верхней частп трубы. Поскольку в этих опытах сетка была охлаждающей, то фаза теплоподвода, определенная по гипотезе стационарности, изменилась па я но сравнению с тем случаем, когда сетка нагрета. Это видно из формулы (48.4), поскольку у охлаждающей и нагревающей сеток знаки разности Тп—Т различны. Тогда, при запаздывании фазы теплоподвода, вектор Q попадает в четвертую четверть, если сетка расположена в области h в. В. Раушенпах На рис. 96, а это соответствует наилучшим условиям возбуждения. В то же время положеппо сетки в области а приводит Q в третью четверть, в которой при малых М Практически отсутствуют области возбуждеппя, поскольку диаграмма устойчивости приближается к виду, показанному па рнс. 29, е.
AAA
![]()
АЛЛ
Рис, 99. Осциллограмма колебаний давления в трубе Рийке по опытам Лемава. Верхняя осциллограмма соответствует £ = 0,25; средний £ = 0,125; нижняя £ = 0,0625,
Резюмируя, можно утверждать, что даже использование столь грубой для рассматриваемых условии схемы явления нестационарной теплоотдачи, как та, которая следует из теоретических расчетов Лайтхилла, позволяет получить все наиболее существенные свойства трубы Рийке.
Помимо уже известных свойств трубы Рийке, Леман, воспользовавшись тем, что он имел возможность регулировать среднюю скорость течепия по своему усмотрению, обнаружил повое ее свойство: по мере увеличения сред пей скорости течения п при постоянном средпем тепло — подводе звучаппе трубы Рийке первоначально усиливается, достигает максимума интенсивности, затем уменьшается и при достижении пекоторой скорости, зависящей от среднего теплоподвода, прекращается.
Прекращение звучания трубы Рийке при некоторой, достаточно большой, скорости может быть понято из написаппых выше формул. Действительно, пусть средний теплоподвод сохраняется поетояппым: <2* = cons^* Тогда, как это следует пз выражения (48.11), ] Q будет уменьшаться, а следовательно, будет уменьшаться тот единственный член выражения (48.13), который дает положительный поток акустической энергии As — В то же время основпое слагаемое, дающее отрицательную составляющую As, М21 Рх 11 vx будет увеличиваться, поскольку с учетом выражения (48.8)
М*рхЫ = № fi^- ii рассмотренном выше случае, прн оптимальном поло — жепии сеткн (£=0,25, т. е. [ иг = | рг | =0,707 с), указанные два члена в сумме (48.13) дадут
4-0,707*c2f 0,2 —sin ty — 5 —, 2 V й а J
Т. е. выражение, которое монотонно уменьшается с увеличением v. Если провести более точный численный ана-
^ As
Лпз, то оез учета возможного изменения ty становится
Равным ~ прн скорости порядка 0,75 м/сек. Эксперимент дал эту величину равпой 0,0 м/сек. Для столь сложного явления падо иризпать хорошим такое совпадение теоретического расчета с опытными данными.
Помилю прекращения звучання трубы Рийке прп увеличении средней скорости течения, тот же эффект наблюдался и нри уменьшении ее до величины порядка
28*
0,15 м/сек. Это, по всей вероятности, связано с тем, что при уменьшении средних скоростей течения и сохраневии средней величины теплоподвода непзмепной происходит сильное нагревание воздуха в окрестности сетки (в том числе и перед ней) и подогрев притекающего воздуха в значительной доле осуществляется за счет естественной турбулентности течения в результате смешепии молей холодного н горячего воздуха еще до пересечения первыми области расположения сетки. Поскольку турбулентное смешение холодных и горячих молей происходит в первом приближении независимо от акустических колебаний, то это приводит к разрыву обратной связи в колебательной системе. Надо заметить, что приведенное предположение не подвергалось количественной проверке и поэтому его следует рассматривать лшиь как одно из возможных объяснений прекращения звучапия трубы Рийке при малых значениях средпих скоростей течения.



 14 августа, 2012
14 августа, 2012  admin
admin  Опубликовано в рубрике
Опубликовано в рубрике