К числу основных интегральных характеристик факела относится его длина. Величина ее сравнительно легко может быть определена из опыта, а также из расчета. Ряд работ, посвященных теоретическому и экспериментальному определению длины факела, упоминался ранее. Для диффузионного факела зависимость длины его от основных определяющих факторов может быть получена из соображений размерности. Для ламинарного диффузионного факела, развитие которого определяется только молекулярным смешением (т. е. для малых значений числа Рейнольдса), как и обычно для молекулярной диффузии, можно принять
TOC o "1-3" h z n d исР, і, ud
Ре — — — = const или — = const—————— ,
I Dl d D
Где d — диаметр сопла, Ре — критерий Пекле, I — длина факела. Значение постоянной в этих формулах зависит от стехиометриче — ского коэффициента реакции и от значений чисел Прандтля и Шмидта (Рг = v/a, Sc = v/D). Таким образом, длина ламинарного факела прямо пропорциональна характерной скорости — скорости истечения газа и квадрату характерного размера — диаметра сопла.
Сохраним ту же форму зависимости длины факела от основных параметров и для турбулентного горения. При этом взамен коэффициента молекулярной диффузии подставим выражение эффективного коэффициента турбулентной диффузии DT = kTud, где k7 —
опытный коэффициент. В соответствии с этим для турбулентного диффузионного факела получим lid — const. В этом случае длина факела не зависит от скорости истечения газа и пропорциональна диаметру сопла. Оба результата — пропорциональность длины ламинарного диффузионного факела скорости истечения и независимость от нее длины турбулентного диффузионного факела — неоднократно подтверждались экспериментально. Результаты опытов различных авторов находятся в хорошем согласии с приведенными выражениями (подробные данные по длине турбулентного факела см. в § 2-1). Некоторые результаты эксперимента показаны на рис. 1-5.
Как видно из графиков, в области малых значений числа Re опытные данные удовлетворительно аппроксимируются прямой, проходящей через начало координат, а при достаточно больших числах Re длина факела сохраняется постоянной. Первое отвечает ламинарному режиму течения, второе — турбулентному. В промежуточной области значений числа Рейнольдса наблюдается более сложная зависимость длины факела от скорости истечения с характерным нелинейным переходом от одной формы к другой. Заметно отличаются факелы и по внешнему виду. Изменения внешнего вида диффузионного факела по мере увеличения скорости истечения сводятся к следующему.
|
Рис. 1-5. Зависимость длины диффузионного факела от скорости истечения газа [Л. 92]. |
Начиная от некоторого значения скорости, в вершине факела появляются заметные местные пульсации, приводящие к локальному нарушению ламинарного фронта пламени. Затем, по мере дальнейшего возрастания скорости, возмущения распространяются вверх по потоку и охватывают все большую область течения. Длина факела при этом заметно сокращается. Наконец, при достаточно высоких значениях скорости истечения возмущения приближаются к устью сопла, факел становится полностью турбулентным. При дальнейшем увеличении скорости длина факела остается практически постоянной.
Для расчета длины факела в переходной области можно воспользоваться интерполяционной формулой, развитой в работе [Л. 32] на основе общих феноменологических представлений о взаимоналожении процессов молекулярного и молярного обмена. Сущность вопроса заключается в следующем.
В переходной области течения выражение эффективного коэффициента суммарной (молекулярной и турбулентной) диффузии запишем по правилу смешения в виде
Где символом е обозначена -доля «неупорядоченности» турбулентного режима. Значение е = 0 отвечает развитому турбулентному режиму, а е = 1 — ла-
|
-а—^v_ |
|
R/R=0,8 |
|
• t |
|
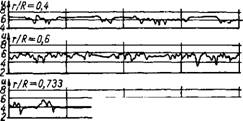
Рис. 1-6. Осциллограммы турбулентных пульсаций за телом — в области перемежаемости [Л. 95]. |
|
Где х — координата состояния; сг — эмпирическая постоянная. Для рассматриваемого случая, как и для течения в трубах, естественно положить х = Re — ReKP, где ReKp — критическое значение числа Рейнольдса [Л. 40]. При х = 0 имеем ламинарный режим (є = 1). При со, очевидно, е-»-0, что отвечает развитому турбулентному режиму. Исходя из этого, можно принять для эффективного коэффициента диффузии следующее выражение: |
Илt/R’0,8 ■
Минарному. Область О < е < 1 соответствует переходной области, в которой молекулярное и молярное перемешивания взаимоналагаются. Во многих случаях є лі 1 — у, где у — так называемый коэффициент перемежаемости [Л. 95], численно равный отношению длительности турбулентного процесса в данной точке к полному времени (см. осциллограммы пульсаций на рис. 1-6).
 Примем в соответствии с экспериментом, что ламинарная и турбулентная формы факела устойчивы. Переход от одной из них (ламинарной) к другой (турбулентной), происходящий при увеличении числа Рейнольдса, опишем оправдавшей себя в ряде случаев простейшей нелинейной релаксационной зависимостью [Л. 321
Примем в соответствии с экспериментом, что ламинарная и турбулентная формы факела устойчивы. Переход от одной из них (ламинарной) к другой (турбулентной), происходящий при увеличении числа Рейнольдса, опишем оправдавшей себя в ряде случаев простейшей нелинейной релаксационной зависимостью [Л. 321
Подставляя его в формулу для длины факела, получаем для переходной области общее интерполяционное выражение
It = п_____________________________
AiT Re + I ——— kr Re j
Переходящее при Re = ReKp и Re -»• оо соответственно в прежние формулы для длины ламинарного и турбулентного факела.
Для проведения численного расчета следует заимствовать из эксперимента значения эмпирических постоянных а[5] и ReKp, a также знать физические свойства газов (число Шмидта) и значение
|
|
Коэффициента турбулентной диффузии. Переход от ламинарного факела к турбулентному происходит так, что длина факела в переходной области проходит через экстремум (максимум — см. рис. 1-5) при некотором значении Re = ReMaKC. Величины ReMaKC и /макс достаточно надежно могут быть определены из эксперимента. Поэтому для определения эмпирических постоянных удобно воспользоваться соотношением ——(—) — 0. Отсюда нетрудно
V d /макс
Прийти к выражению, связывающему постоянную а2 со значением Re
ІЛ ——————————————————————- .
ReMa кс [r
EMaKc^rSc — 1]
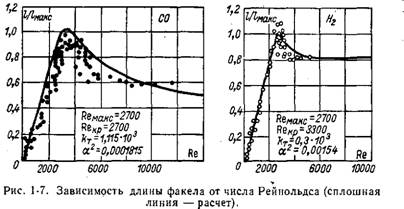
Определенные таким образом из конкретного эксперимента величина а2 и значение ReKp позволяют рассчитать зависимость длины факела от Re во всей области течения. Как видно из рис. 1-7, расчетная кривая удовлетворительно описывает данные эксперимента. Принятые значения ReKaKC и ReKp указаны на рисунке. Значение коэффициента kT в формуле DT — kT ud может быть заимствовано, например, из работы [Л. 35], согласно которой величина kT ж Ю-3 (точнее kT = 0,0009 — ь 0,0013). В расчете учтена также приближенная зависимость значения kT от отношения плотностей газа в струе и окружающем пространстве в виде
|
0,5
|
Вытекающая из условий постоянства начального импульса [Л. 101 ].
Конечно, приведенный здесь интерполяционный расчет лишь в первом приближении отражает реальную закономерность изменения длины факела. Существенно, однако, то, что он качественно правильно описывает картину нелинейного критического перехода от ламинарной формы течения к турбулентной. Как и в других случаях такого перехода, типичными для кризиса течения являются своеобразное затягивание ламинарного режима и последующий нелинейный переход к турбулентному режиму. Внешне это проявляется в том, что кривая зависимости длины факела от скорости истечения подходит к постоянному значению для турбулентной области не снизу, а сверху.



 13 августа, 2012
13 августа, 2012  admin
admin 
 Опубликовано в рубрике
Опубликовано в рубрике