Рассмотрим диффузионное горение в области турбулентного смешения двух спутных плоскопараллельных потоков газа — топлива и окислителя. Схема факела аналогична изображенной на рис. 1-2 для ламинарного горения. Она отличается, однако, от ламинарной прямолинейностью фронта пламени. Это следует из приведенного ниже решения, но может быть, как об этом говорилось в предыдущем параграфе, обосновано простейшими соображениями размерности.
Действительно, для рассматриваемой (автомодельной) задачи о турбулентном фронте пламени в исходных уравнениях и граничных условиях отсутствует величина размерности длины (размер сопла или отношение v/u0 — в ламинарном факеле). Поэтому лю-
Ри (и —
Бая безразмерная функция, например г =———————————— — , не
Может зависеть от координат хну (или £ и у) в отдельности, а будет определяться безразмерным аргументом вида у! х в физической яту/У^ в приведенной плоскости. В частности, на фронте пламени — поверхности постоянных значений температуры, скорости, функций Ft и т. п.— должно быть г/ф = const или Уф = const хф.
Аналогично этому в задаче Стефана [JI. 85] координата фронта плавления пропорциональна корню из времени (х ~ в методе эквивалентной задачи роль «времени» играет координата |). Это сопоставление поясняет аналогию между задачами теории факела и теплопроводности с «движущейся границей».
Заметим также, что рассматриваемая задача о плоском фронте пламени в техническом плане представляет собой схематизацию течения и горения в начальном участке осесимметричного или плоского факела конечного размера (в общем случае — спутного). Для обоих течений (k = 1 и k = 0) при относительно малой толщине области смешения задачу можно считать плоской. Решим ее методом эквивалентной задачи теории теплопроводности (см.
Выберем функции F; в следующем виде, удобном для расчета:
Для всей области течения
^ Р" ("-"-«)
Р + -И+,* К.-"—) для зоны / (формулы слева) и зоны II (справа) р рЦСр(Г-Гф) и р 9ucp(T-T_J)
А также
Р _ риса___________ р _ рисв
" Р+ оо" + ooCЈJ, + ОО 8 Рф"фСвф ‘
Индексы + со и — со относятся здесь соответственно к невозмущенным потокам топлива и окислителя, индекс «ф», как всегда,— к фронту пламени.
Исходная система уравнений для плоского течения (k = 0) имеет вид
(2-5)
DU di/» V
С граничными условиями:
У< О, F==Ft = Fa = 1, */>О, ґ = 0, ґп — 1, = 0;
‘ F = Л = Fa = = 0 при «/ = + С»,
|
При = 0 |
|
(2-6) |
|
При > 0 р |
|
F = FU = F а |
О, і7,, = = 0, ^- = 0 при i/=-co, 0, = 1 при г/ = г/ф. К этим условиям следует добавить соотношение на фронте
І
О/г
/ф "" /ф
Заменим в равенстве (1-7) производную по нормали к фронту
|
4-COS (и, х) + -7- cos (л, дх ду ду |
|
Дсб ду |
|
(2-7) |
Д_ дп
С учетом неравенств д/дх діду (известное свойство пограничного слоя) и cos (и, х) ^ 0, cos (и, у) » 1 производной по координате у. Поэтому взамен (1-7) примем приближенно (при DTa^DT6 — равенстве коэффициентов турбулентной диффузии компонентов)
__ <2 дса
Ф дУ
Решение уравнений (2-5) имеет вид
^ = + rf _ (2-8)
Где Л, и В, — постоянные интегрирования; = —приве
Денная координата, разная для различных уравнений, причем
Lu=l = = — эмпирическая постоянная. В соответствии с этим і|) = у! V І и ф9 = tyg = y = Ф
Постоянные интегрирования At и В{ легко находятся из граничных условий. ,
В результате решения соотношения (2-8) могут быть представлены следующими выражениями:
|
(2-9) |
|
F (ф) = — |
|
Р+„ |
Ри (и —
= -^(1 +erf ф),
= Fa(W =
Тф) ? + +
|
Риср (Т — Тф) |
|
Р иса |
|
(2-10) |
^ егГ(фуТ)-егКффУТ) I —erf (Фф уЪ)
|
= fe(t) = |
|
РфЧфСдф |
Рис,I (T — 7[10]Ф)
Рф" г.0Р(тф-т—)
1 + erf (ф /а ) 1 + erf (фф /7)
Из этих выражений первое (2-9) относится ко всей области течения, тогда как (2-10) и (2-11) относятся соответственно к зоне I и зоне II, в каждой из которых распределения плотностей потоков энтальпии и вещества подобны между собой.
Если теперь, как в § 1-4, пренебречь различием между средним (в смысле Рейнольдса) значением произведения и произведением средних, т. е. положить, например, ри^р-и, ри[11]^р-и2 и т. д., то выражения (2-9) — (2-11) с учетом равенства рТ — const, а также ср « const представят собой уравнения, из которых можно найти распределение всех первичных величин — плотности газа, скорости, температуры и концентраций. Следует отметить, что приближение рия&р-и и т. д. является общим для всех расчетов турбулентных струй и факела. По существу оно же принимается всегда при обработке опытных данных — при расчете профиля скорости и других величин — исходя из экспериментально определенных значений динамического давления ри2 и температуры Т = = const/p.
|
(О |
С учетом этих замечаний из выражений (2-9) — (2-11) получим квадратное уравнение относительно распределения скорости в поперечных сечениях факела: для зоны I
[i;J-[m + F{l-iol)]JL + m{l-ml)Fl-wlF(l~m) = 0; (2-12) ■
Для зоны II
FjLy_fmu) +ІІФ(т пр 1JL +
и0 I 11 и„ 11 I 11 «о
— ‘) ^п — 0 — т)<о^ — 0. (2-13)
Решения этих уравнений имеют вид: для зоны I
|
, (2-14) |
|
|
|
ТГ (ш11 -1)/гП-ттП +4 (1-т)«1} Ш ир |
|
И |
|
, (2-15) |
Т + (1 — ш, ) F, + ]/"[(! — со, ) F, — /я]* + 4 (1 — т) <о, F
И
Где
+ If т* + 2 (1 — ш) Ш, [1 + erf (фф)]
«п
Заметим, что здесь и далее перед корнем выбран знак плюс, так как во всех случаях горения параметры (о, и а>п больше единицы. Знак минус соответствовал бы не рассматриваемому здесь случаю эндотермического процесса (например, конденсации и т. п.).
|
И ф _ |
Из распределения скорости в факеле без труда находятся все остальные переменные. Окончательные выражения для них сведены для удобства в табл. 2-1, в которой (как и в приведенных выражениях для плотности газа) обозначено:
|
Тф Р+~ Тф Р-оо ‘ шп О) =—= _±_ и) =—=————- ш = _li т — . 1 Г+00 Рф " РФ «, " + м Таблица 2-1
|
Кроме того, в табл. 2-1 для краткости принято
/6 = т + (! ~wi)Fi> f7 = {l~Mi)Fi-m’
Л = "ф (шп -l) Fn+ mwu ‘ Л = "ф (щп -1) Fu ~ тти •
Выражения, приведенные в табл. 2-1, значительно упрощаются в частном случае т = О, когда спутный поток отсутствует (и_м = 0). Эти выражения указаны в табл. 2-2.
Полученные выражения как в общем, так и в частном случае содержат неопределенную до сих пор величину — приведенную координату фронта пламени фф = уф/2 ]Аф. Для отыскания ее следует воспользоваться условием на фронте (2-7). Вычисляя с помощью выражений, представленных в табл. 2-І, производные от концентраций топлива и окислителя, получаем
|
Дса |
Са, +по |
Dca |
1 |
‘ (Р") + оо |
RiF, |
+ F d |
||
|
Ди |
2 УТ |
Гіф |
21/? |
Ри |
Гіф |
1 ‘ ^ • |
Р" |
» |
|
Дев |
С6 » |
Dc6 |
" (Р")+оо |
DFn |
+ F — + " гіф |
(ри) + « |
||
|
Ду |
2 УЇ |
Гіф |
2VT |
Р и |
Гіф |
Ри |
Имея в виду, что условие (2-7) должно удовлетворяться на фронте пламени (ри — рфиф и Г:ф = 0, f,, = 1), получаем
" + «, ехр ф|а)
~ W г ‘ " — __ J
|
Дса ду |
|
‘■а. +• |
]/+£ "Ф I —erf (фф Y" )
|
Дев ду |
"Фш11еб. ___________________ ехр (- ф|з)
Ф УяЕІИф(<вп + 1)-т, вііи + -] 1 + erf (ффКо)
Подстановка этих выражений в (2-7) приводит к трансцендент ному уравнению относительно координаты фронта фф
|
(2-16) 2. Тем са |
І-erf (фф/Г)
(т + Mf _
Т + (">п + і)Л« 1+erf (ффІ^Г)
Где М = + 2 (1 — m)(0, (1 + erf фф), a fc =
Б, — «
Мым задача доведена до конца.
В случае истечения топлива в неподвижное пространство (и^^ = = 0, т = 0) формула (2-16) несколько упрощается:
1+erf (ффіМ
Где
— Q |/2о
— Наконец, при т — 0 и а = 1 уравнение для определения координаты фронта а|)ф имеет совсем простой вид:
; "-■ — ; wf|t_,+tit=^Eia.
На рис. 2-2 показана зависимость фф ф) для нескользких значений постоянной о и Параметра т.
Как видно из рис. 2-2, эта зависимость хорошо согласуется с результатами физического анализа явления. Действительно, во всех случаях (при заданных т и а) с ростом стехиометрического комплекса f>1 абсолютное значение координаты 1|>ф растет. При этом величина і|}ф < 0 (начиная с весьма малых значений комплекса). Это значит, что фронт пламени расположен в области окислителя (Уф/Хф < 0) и тем дальше от оси (у = 0), чем больше значение стехиометрического комплекса При постоянном значении и
Любом заданном значении параметра т (например, при т — 0 или т = 0,5 на рис. 2-2, а) с ростом значения о фронт пламени смещается в сторону потока топлива, т. е. приближается к оси у = 0. Аналогично этому при заданных значениях Pi и а (например, а = 0,7 на рис. 2-2, б) увеличение т ведет к уменьшению фф, поскольку ширина области смещения при сближении скорости обоих потоков уменьшается. Отметим также существенное отличие результатов расчета для т = 0 и т = 0,5.
На рис. 2-3 для примера построены профили относительных значений температуры и скорости в пограничном слое. Эти кривые иллюстрируют влияние параметра а на местоположение фронта пламени. Следует иметь в виду, что в физических координатах это влияние будет менее заметно, поскольку изменению координаты г|?ф пропорционально изменение arctg (Уф/хф).
Для иллюстрации в табличке приведены значения углов для т = 0,5 (по рис. 2-3) и т — 0 (в расчете принято со, = о)п = 6, 1, Q = 11, а также С — 0,025 для m = 0,5 и С = 0,04 для т — 0, где С = УТ/х эти значения примерно соответствуют горению метана в воздухе).
Значения эмпирических постоянных С = С (т), а также а должны быть заимствованы из опыта. Если ориентироваться на данные по струям, то 0,7 ч-0,85. Из приведенных примеров можно заключить, что в реальных условиях (в физической плоскости течения) трудно обнаружить влия-
|
Рис. 2-3. Распределение скорости и температуры в плоском пограничном слое при горении неперемешанных газов. |
Ние значения а на местоположение фронта пламени, так как точность измерений в турбулентном факеле позволяет определить координаты фронта с точностью порядка нескольких градусов.



 13 августа, 2012
13 августа, 2012  admin
admin 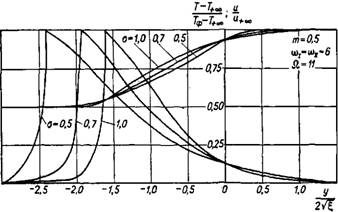
 Опубликовано в рубрике
Опубликовано в рубрике