При обсуждении особенностей турбулентного горения газа [Л. 49; 52; 65; 78; 98; 100] на первый план, как правило, выдвигаются вопросы интенсификации процессов переноса (теплопроводности и диффузии) под влиянием турбулентных пульсаций скорости. Обсуждаются, в частности, искривления поверхности фронта пламени вплоть до так называемого эстафетного распространения его путем заброса горящих молей в свежую смесь и т. п.
Наряду с этим важным для выяснения механизма турбулентного горения явлением большое значение имеет влияние пульсаций температуры на макроскопическую кинетику реакций в турбулентном потоке. Указание на несоответствие между наблюдаемой средней скоростью реакции и ее расчетным значением, отнесенным к средней температуре, встречается в работе Я. Б. Зельдовича [Л. 47]. Следуя в основном работе [Л. 26], рассмотрим сущность и в первом приближении количественную сторону этого явления, играющего большую роль в турбулентном горении факела (как и вообще при протекании химических реакций в турбулентном потоке).
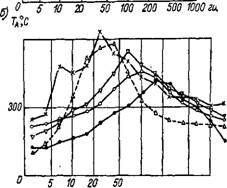
Вследствие турбулентного перемешивания свежей смеси с продуктами сгорания в зоне реакции происходят непрерывные пульсации температуры. На рис. 5-1 приведены кривые спектрального распределения интенсивности пульсаций температуры в турбулентном диффузионном факеле [Л. 57]. Как видно из рисунка, частотный спектр пульсаций факела близок к спектру, характерному для турбулентных струй. Из работы [Л. 57] следует, что вблизи фронта пламени (в области максимального значения средней температуры) отношение Тмакс/Т’макс достигает 0,5 и выше.
Отвлекаясь от сложного в действительности характера турбулентного спектра пульсаций температуры, рассмотрим для простоты выделенные монохроматические колебания температуры. Примем, что скорость реакции мгновенно следует за изменением температуры, т. е. соответствующее время релаксации пренебрежимо мало. В этом предположении, близком к действительным условиям протекания реакций горения в турбулентном потоке, наиболее часто проявляется своеобразная асимметрия колебаний скорости реакций. Из-за нелинейной экспоненциальной температурной зависимости константы скорости реакции (закон Аррениуса) симметричным относительно среднего значения колебаниям температуры будут отвечать резко несимметричные колебания скорости реакции со значительным (иногда на несколько порядков) сме
щением в область повышенных значений. Конечно, в реальном турбулентном спектре влияние температурных пульсаций на кинетику реакций будет чрезвычайно сложным, однако качественная сторона нелинейного эффекта
Сохранится — рост скорости реакции при повышении температуры будет превалировать над падением ее при снижении температуры.
Заметим, что подобный эффект сохраняется и в других процессах, скорость которых нелинейно зависит от температуры (например, при излучении). В частности, и это наблюдается в эксперименте (см. § 10-2), аналогичное значительное увеличение эффективного значения электропроводности имеет место в турбулентных потоках проводящего газа из-за нелинейной зависимости проводимости от температуры
[0~ехр(-А)].
В принципе сложный временной ход скорости реакции учитывается при статистическом описании турбулентного горения [JI. 52; 65; 66; 77; 100], но такой путь не привел пока к конкретным результатам. Поэтому для оценки рассматриваемого эффекта обратимся к простейшим колебаниям.
С этой целью свяжем между собой актуальное,
|
Л — к х-5 +-S |
|
—1 О-2 V-3 |
|
Ф |
|
" / ЧД "л / ? * II ‘ V |
|
Та, С |
|
V\ |
|
J |
|
/I F* ‘і’ l/l |
|
300 |
|
■Я |
|
100 200 500 1000 ги, |
|
Рис. 5-1. Кривые спектрального распределения интенсивности турбулентных пульсаций температуры в диффузионном факеле: а — При х = 4 |
|
Ы |
|
1_ — при у = 0, f = 990° С; 2 — при у = 5 мм, Т = 1010" С; 3 — при у 10 мм, Г = 1200° С; 4 —■ при у = 15 мм, Т = 1340° С; 5 — при у = 20 мм, Т = 1090° С; 6 — при у = 25 мм, Т = 550° С; б — при X = 8 (— при у = 0, Т = 980" О, 2 — при_ у = 5 мм, Т = 1140° С; 3 — при у = 10 мм, Т = 1390° С; 4 при у =а 15 мм, Tj= 730° С; 5 — при у =» 20 мм, Т — 160° С. |
А затем и среднее значение скорости реакции в турбулентном потоке со значением ее, рассчитанным по осредненной (в смысле Рейнольдса) температуре. Поскольку экспоненциальная зависимость скорости реакции от температуры преобладает над сравнительно слабой степенной зависимостью от концентрации (также
пульсирующей во времени в результате турбулентного перемешивания), ограничимся учетом изменения константы скорости реакции. Температурную зависимость последней представим, как обычно, формулой закона Аррениуса:
* (Л ехр [—!_]. (5-3)
Формула (5-3) определяет изменение во времени мгновенного значения константы скорости реакции. Среднее ее значение для
Установившегося (в среднем) процесса может быть выражено в виде
Е
Dt.
RT (t) J
H
Где т — достаточно большой (по сравнению с периодом пульсаций температуры) интервал времени. Определим также среднее значение температуры (Т = Т — Т’):
— і
J T(f)dt
T0
|
K (Т) = kb ехр |
И соответствующее ему значение константы скорости реакции:
£оехр(——- . (5-4)
1
Я— J T(t)dt
Обозначим отношение осредненного во времени значения константы скорости реакции k [Т (t) ] к значению ее, соответствующему средней температуре k [Т (/) ], символом
К(Т) (5-5)
K(T)
Для качественной оценки допустим, что актуальное значение температуры Т (t) изменяется со временем по одной из простейших симметричных форм колебаний, например прямоугольной (рис. 5-2). Тогда — ив этом основное содержание эффекта — нелинейный характер зависимости k (Г) приведет к асимметричному колебанию k (t) с существенным преобладанием повышенного относительно k (Т) значения над пониженным. То же самое сохранится и при синусоидальных колебаниях. С физической стороны эта асимметрия колебаний значения k (Т) относительно величины k (Т) .(или значения •/■ относительно единицы) объясняется тем, что повышение температуры на величину 7" = Т — Т вызывает относительное увеличение значения константы k по формуле (5-4), существенно превышающее уменьшение ее при снижении темпера — — туры на ту же величину Т’. Иными словами, для трех значении
Температуры Т + Т’, Т и Т — Т’ можно написать неравенство
K (Т + Т’) k(T__ Т’)
|
ЦТ) |
— — т ‘———— 1 > 1————— v, справедливое для практически
Интересной области аррениусовской кривой (до перегиба).
Приведем теперь количественную оценку эффекта. Ограничиваясь для простоты случаем прямоугольного симметричного во времени колебания температуры с амплитудой Т’, запишем среднее значение k (7) в виде
K(T + Г) + k(T—T’) = 2 ~
K{T)
|
+ ехр |
|
RT
|
Ехр
RT
Т
Itfifl-
|
1 |
|
Г Т Е |
|
+ |
|
Ехр |
|
RT |
|
RT |
Рис. 5-2. Схема колебаний температуры и константы скорости реакции.
Примем, что пульсации температуры сравнительно малы: ТЧТ <<( 1; тогда вместо (5-5), используя приближенное разложение в показателе экспоненты
1 + -=- , можно написать Т
1 ±
+ ехр
RT
Температуры Т IT и чем меньше средняя величина безразмерной температуры RT/E. _
Рассмотрим численный пример для значения Т’/Т = 0,1. Для нескольких значений RT/E, указанных в таблице, соответственно получим:
|
RT/E |
0,03 |
0,05 |
0,1 |
0,2 |
Ft |
3,33 |
2 |
1 |
0,5 |
|
Т, °К |
300 |
500 |
1000 |
2000 |
* |
14 |
3,6 |
1,54 |
1,13 |
Как видно из этих данных, при вполне реальных значениях Т (при Е = 20 ООО /скал/моль — град) и умеренной величине Т/Т значения отношения х весьма большие. Порядок величины х остается тем же, если взять для расчета, например, треугольную или наиболее правдоподобную с физической точки зрения синусоидальную форму колебаний. В этом случае приближенно можно положить х = ф ch где ф — формфактор колебаний, равный примерно Ф = 1, ф = 0,7 и ф = 0,5 соответственно для прямоугольной, синусоидальной и треугольной форм колебаний.
Для приведенного выше примера Т’/Т = 0,1 и ф да 0,7 (колебание близко к синусоидальному) взамен х = 3,6 (при Ф = 1) будем иметь х да 2,2. В случае сильных пульсаций температуры (Т’/Т да 1) в качестве верхней предельной оценки из формулы (5-6) получим (при ф = 1, Г да Г’)
При RT/E = 0,05 и 0,1 значения х соответственно будут равны х да 104 и х да 75. Даже при RTIE = 0,2 значение х = 6.
Приведенный приближенный расчет и численные примеры дают достаточно наглядное представление о порядке величины рассматриваемого эффекта. Обратимся поэтому к краткому обсуждению физических условий, в которых он может проявляться.
Во всех случаях, когда в зоне протекания химической реакции из-за турбулентного смешения будут происходить пульсации температуры, локальное повышение скорости реакции при 67" > 0 в среднем будет всегда значительно превышать ее снижение при бТ’ < 0. Результатом этого будет более быстрое по сравнению с ламинарным потоком распространение пламени. При этом, как и всегда, когда речь идет о смешении свежей горючей смеси с продуктами сгорания, местное повышение температуры будет сопровождаться местным балластированием смеси (снижением действующих концентраций). Однако преобладание более резкой (экспоненциальной) зависимости скорости реакции от температуры над более слабой (степенной) зависщрстью от концентрации, как
и в других случаях (возврат продуктов горения при стабилизации пламени и др.), обеспечивает прогрессивное, ускоряющее реакцию действие этого смещения.
Таким образом, обсуждаемый эффект играет, видимо, существенную роль в явлении турбулентного распространения пламени, обусловливая, в частности, известную из опытов зависимость скорости турбулентного распространения пламени от кинетических факторов (от нормальной скорости пламени и др.— см. [Л. 50; 100]). Особенно велико может быть ускоряющее действие пульсаций температуры при распространении пламени в неподвижной газовой смеси, и при возникновении в последней турбулентного движения, приводящего к перемешиванию продуктов сгорания со свежей смесью и, следовательно, к пульсациям температуры, сопровождающим пульсации скорости. Представляется вероятным, что именно этим частично объясняется механизм ускорения пламени в трубах, приводящего к образованию детонационной волны, а также влияние шероховатости и других факторов на возникновение детонации в опытах К — И. Щелкина [Л. 98; 99]. Не рассматривая здесь эти вопросы, сформулируем общий физический вывод, имеющий принципиальное значение.
В турбулентном потоке, помимо известных кинематических факторов, в зоне горения проявляется прямое, в качественном отношении значительное воздействие турбулентных пульсаций температуры на эффективную скорость протекания химических реакций.



 13 августа, 2012
13 августа, 2012  admin
admin 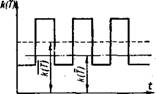
 Опубликовано в рубрике
Опубликовано в рубрике