Сильное воздействие на пламя могут оказать скрещенные электрическое и магнитное поля. Схематически такое течение показано на, рис. 9-1.
Расчет течения для случая Е > иВ и, следовательно, / = оЕ может быть выполнен аналогично предыдущему.
Для автомодельного решения, помимо задания зависимости
Магнитного поля от координаты х в виде В = В0/f х, следует принять также и для электрического поля Е = EJ ]/ х. При этом как исходные уравнения, так и уравнения в переменных Дородницына остаются теми же, что и в предыдущей задаче. Иной вид примут только уравнения баланса сил и тепла для эффективной зоны:
[l-fL _ *L| ] = ,ЕВЫ. 0-25)
LI ду ф1 ду |ф2_1
№ф/)ф = + 1. (9-26)
°У |ф1 LI ду ф! ду |ф2]
Тогда как граничные условия не изменятся. Сохранятся теми же выражения для безразмерных’ профилей скорости, температуры и концентраций в областях по обе стороны от эффективной зоны взаимодействия. Из этих выражений с учетом равенств (9-7) — (9-15) и (9-20) можно получить выражения, определяющие значения скорости и температуры внутри зоны взаимодействия:
= 0,5 {(1 + т) Г1 + erf (фф) +
" + оо ( L 1+mJ
+______ Lr^’CH)______________ ————————— (9-27)
[erf (Ф)]ф erf [(Фф 1/Рг)]ф (1 — 2ГФ0) (Гф — 1) 1 + « j
Н
|
Мц/зсЩ,/Sc_ |
|
(9-28) |
Г» 9
1—erf (ффі/Sc)
(erf (Ф)1ф (1 — 2Тфв) (Тф — 1)
Pr 1 — erf2 (фф V Рг) причем безразмерные параметры Nly х, Q определяются формулами: aEaBaL
Q
Первый из них характеризует отношение объемной электромагнитной силы к динамическому давлению, второй — отношение джоу-
Лева тепла к плотности потока химической энтальпии, а третий — отношение энтальпии единицы массы газа к химической
|
‘Ф(х-О)
Рис. 9-6. Изменение температуры в зоне горения в зависимости от напряженности электрического ПОЛЯ. 1 — при <7=10* ккал/кг; 2 — при <7 = 0,8 ккал/кг-,3 — при q =0,6 ккал/кг; 4 — при <7 = 0,4 ккал/кг. |
Энтальпии. Эти три параметра Nlt *, Q определяют значения температуры и скорости в зоне горения. В зависимости от приложенного электрического поля параметр может принимать положительное или отрицательное значение, так что возможно как ускорение, так и торможение газа в зоне взаимодействия с полем. Торможение факела привело бы, по-видимому, к резкому сокращению его длины.
Результаты расчета скорости в эффективной зоне в зависимости от напряженности электрического поля представлены на рис. 9-5. На нем нанесена серия кривых иф = f (*), рассчитанных для различных значений теплотворности газа. Зависимость температуры в зоне горения от напряженности электрического поля приведена на рис. 9-6. На рис. 9-7 показано распределение скорости и темпе-
|
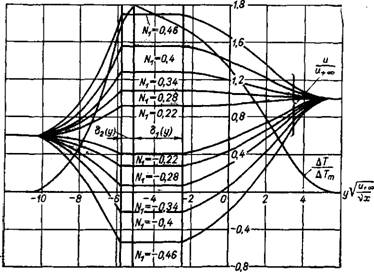
Т-Т+оа. U Tfffl+oo Uroa
Рис. 9-7. Распределение скорости и температуры при различных Значениях напряженности магнитного поля. ши = 0,6,и + 00= 10 м/сек, р+00= 1,25 кг/л3, Г± = 300° К, с’по=0.25 кг/лг> сбо= 0,23 кг/кг, д = 10′ ккал/кг, Е„ = 3800 е/л. |
|
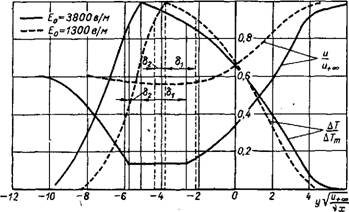
Рис. 9-8. Распределение скорости и температуры при различных Значеннях напряженности электрического поля. тц = 0.6, и + х, — 10 м/сек, р+ю = 1,25 кг/м’, 7"±ос = 300° К. са_ +00 =■ — 0,25 кг/кг, с6> +<ю = 0,28 кг/кг, В0 = 0,01 еб/м’, д = 10′ ккал/кг. |
Ратуры в поперечных сечениях пограничного слоя при различных значениях магнитной индукции и напряженности электрического поля для весьма малых значений параметра х, что физически соответствует сгоранию высококалорийных смесей при умеренных значениях поля и различных значениях параметра Nt. В этом случае профиль температуры практически не изменяется, а профиль скорости претерпевает заметные изменения. Расчет показывает, что скрещенные поля могут ускорить (большие положительные значения N1 > 0) или замедлить (большие отрицательные значения Nt) течение газа.
На рис. 9-8 показано для двух значений х влияние электрического поля. С ростом поля фронт пламени смещается во внешнюю сторону пограничного слоя.
Как видно из этих примеров, с помощью скрещенных электрического и магнитного полей можно в сравнительно широких пределах воздействовать на температурный режим и аэродинамику диффузионного газового факела. Разумеется, что в рассмотренных примерах не учитывается возможное в принципе влияние полей на скорость реакций горения.



 13 августа, 2012
13 августа, 2012  admin
admin 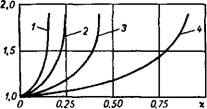
 Опубликовано в рубрике
Опубликовано в рубрике