14 августа, 2013 
admin What exactly is a fluid?
• Fluid is a term used for both liquids and gases.
• Vapor is an inexact term but is generally understood as gas near the saturation condition where liquid and gas phases exist together.
• Water and steam, air and flue gas, and fuel oil and fuel gas are the main fluids operating in a boiler.
Ideal and real fluids. An ideal fluid, which of course does not exist, is one that has no viscosity or surface tension and is incompressible. However, fluids with low viscosity, such as water and air, can be considered as ideal fluids under certain conditions to simplify the analysis. Real or practical fluids are the opposites of ideal fluids and are commonly found.
Newtonian and non-Newtonian fluids. Newtonian fluid is one in which the shear stress is directly proportional to the rate of shear strain or velocity gradient. Non — Newtonian fluid is the opposite (Figure 2.16).
Types of flow.
• Steady and unsteady flows
• Uniform and nonuniform flows
• Laminar and turbulent flows
• Compressible and incompressible flows
|
|
FIGURE 2.16
Types of fluids.
• Rotational and irrotational flows
• One-, two-, three-dimensional flows
The most basic and universally applied law in fluid flow is the Bernoulli’s equation, which is essentially an energy conservation law—the sum of pressure and velocity/kinetic energy in a flowing fluid is constant and mutually convertible. Stated differently, for a steady and ideal flow of incompressible fluid, the total energy comprising pressure, kinetic, and datum energies is constant at any point in the fluid.
Where
P = pressure head in meters (pressure in kilograms per square meter X specific volume in cubic meters per kilogram)
V = velocity in meters per second Z = elevation in meters
Material Balance or Continuity Equation
Another important law governing the fluid flow is the continuity equation or material balance:
Where Q is the flow in cubic meters per second and A is the area in square meters. It follows that as the fluid flows from body 1 to 2
|
(2.24) |
Q = AM = A2V2
Usually, adiabatic flow is assumed but occasionally isothermal flow may be more correct.
Flow through Nozzles and Orifices
• As the fluid passes through a nozzle of an orifice, a drop in pressure and an increase in velocity take place simultaneously.
• For incompressible fluid flowing through a nozzle where the approach velocity is negligible, the outlet velocity is
|
|
(2.25)
Where A p is the difference in pressure head in meters.
— Thus, the velocity of a free jet is dependent only on the differential pressure head that causes the flow, and is independent of the density.
— If the density difference is <5% at the discharge, mainly arising from a small pressure difference, the fluid can be considered as incompressible and Equation 2.25 can be used.
For a compressible fluid flowing through the nozzle, the outlet jet velocity is V2 2g X (h1 — h2) = 91.53VAh m/s
Where Ah is the enthalpy difference in kilocalories per kilogram.
— For steam, Ah can be read from the steam tables or the Mollier chart.
— For other compressible fluids where perfect gas laws are applicable, it is calcu-
Lated as
|
(k-1)/k |
|
Pi Pi |
|
M/s |
|
K |
|
1 |
|
Pi |
|
K -1 |
|
V, = 91.53 |
 |
|
 |
|
|
|
Where k = Cp /Cv, the ratio of specific heats at constant pressure and volume, and p1 and p2 are upstream and downstream pressure heads in meters, respectively.
The smallest cross section of a nozzle is called the throat, where velocity is the highest and pressure the lowest. As the pressure is lowered the velocity keeps increasing at the throat until it reaches the acoustic velocity. This is called the critical flow pressure (different from the critical pressure).
Any further reduction in the back pressure does not increase the velocity, and hence the maximum flow in kilograms per second is fixed. However, beyond the throat, as the pressure is lower the specific volume increases and supersonic velocities will result.
For any gas or vapor the ratio of critical to inlet pressure is constant, and it varies from 0.5 to 0.6.
For perfect gases it can be calculated as
K/(k-1)
|
(2.28) |
|
Pi |
—1 : + 1J
Where k is a constant 1.4 for air and varies as 1.31 and 1.26 for steam at 7 and 70 bar, respectively.
Critical pressure for air is constant at 0.53 of absolute inlet pressure and varies as
0. 544 at 7 bar and 0.551 at 70 bar for saturated steam and 0.553 for SH steam.
The flows resulting from the preceding equations are theoretical and do not take into account an important factor, friction. To arrive at the actual velocity, the ideal velocity should be multiplied by the velocity coefficient Cv, which is equal to ^ 1—Cd, where Cd is the drag coefficient. Cv is 0.98-0.99 for thin orifices.
A jet of fluid issuing from a square-edged orifice attains a minimum cross-sectional area before enlarging again. This minimum area of jet is called vena contracta, and the ratio of the area of vena contracta to the area of nozzle is the contraction coefficient Cc. For thin orifices, Cc is —0.62. Overall the product of Cc and Cv is the flow coefficient Cq.
• Friction comes into play whenever there is flow of a fluid.
• Friction loss is dependent on the flow pattern (laminar or turbulent), fluid properties, the size and form of conduit, and surface condition of the conduit.
• In laminar flow the adjacent layers of fluid flow over each other with no slip at the walls, whereas in turbulent flow there is random flow of particles with shearing of adjacent layers. The layer adjacent to the wall is too thin, and the fluid experiences the roughness of the wall.
• Moody’s friction factor captures the effect of friction for all conditions.
The friction loss inside a conduit is given by Darcy’s formula in meter head
|
(2.29) |
V2
2gD;
Where
|
F L V2/2g Di |
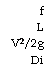Moody’s friction factor or four times Fanning’s friction factor : length of pipe/conduit in meters velocity head in meters
Pipe bore or equivalent diameter for noncircular conduit (flow area/wetted perimeter) in meters.
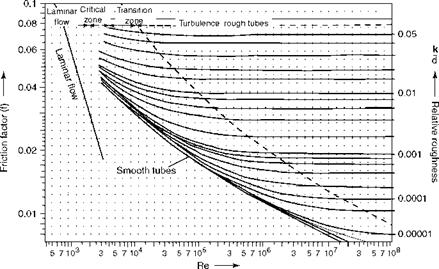
Based on Re and the relative roughness, friction factor f is calculated from Figure 2.17 for turbulent flow, which varies in a narrow band of ~0.020-0.025 for normal applications of steam and water.
|
Reynolds number FIGURE 2.17 Friction factor (f) versus Reynolds number (Re). |
|
Equivalent diameter (de) (in.) |
FIGURE 2.18
Relative roughnesses of pipe materials.
• The relative roughnesses (k/de or e/de) for various materials and equivalent diameters are given in Figure 2.18.
• For laminar flow f = 64/Re.
• In practical calculations the effect of aging of pipe should be included by increasing the roughness suitably.
These losses form the major portion of total piping losses as the straight runs in a boiler plant are relatively short and the fittings are many. These losses can be calculated as the equivalent lengths of straight pipes or the number of velocity heads. For valves, these data furnished by the valve makers are both empirical and approximate. The loss in valves is given in meter head by
V2
Hf = fL
2gDi
Or
|
Hf |
XT fL N™ь
Where NVH is the number of velocity heads.
TABLE 2.4
Equivalent Lengths for Restriction
TOC o "1-5" h z Restriction L/D
Entrance 20
Exit 40
Close return bend 50
180° Bend 30
90° Bend 25
45° Bend 15
90° Short-radius elbow 24
|
TABLE 2.5 Bend Factors
|
TABLE 2.6
Expansion Factors
Expansion angle 20 40 60 80 90
Fe 0.45 0.9 1.2 1.2 1.1
Typical equivalent lengths as the number of diameters are given in Table 2.4.
Bends cause two types of losses. In addition to the friction loss in the developed length of the bend, there is loss due to change in the direction of flow, which is calculated in meter head using the formula Fb X VH, where the bend factor is taken from Table 2.5. It is important to increase Fb by 70% when the bend is immediately followed by a short straight pipe less than 4D.
These losses put together with head are considered as 1.5 VH in meters. These are the combined shock losses at the entry and exit of tubes and pipes.
This loss is due to reduction in the cross section of flow area. The loss is neglected when the included angle is < 30°. When the angle is more than 30°, the loss is calculated in meter head as 0.5 (1 — A) VH, where A is the ratio of smaller to larger area.
This loss in meter head due to enlargement of cross section is Fe(1 — A)2 VH, where VH is calculated on smaller area (Table 2.6) and Fe is taken as per Table 2.6.
Duct losses are also calculated in a similar way as pipe losses. But the shapes and the configurations are many and hence not covered here.
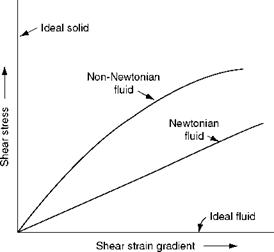
Опубликовано в рубрике 
