12 августа, 2013 
doctype 8.1 Estimating surface area of heat transfer equipment; overall heat trans
Fer coefficient; approximating overall heat transfer coefficient in water tube boilers, fire tube boilers, and air heaters; log-mean temperature difference
8.2 Estimating tube-side heat transfer coefficient; simplified expression for
Estimating tube-side coefficient
8.3 Estimating tube-side coefficient for air, flue gas, water, and steam
8.4 Estimating heat transfer coefficient outside tubes
8.5 Estimating convective heat transfer coefficient outside tubes using
Grimson’s correlations
8.6 Effect of in-line vs. staggered arrangement
8.07a Evaluating nonluminous radiation heat transfer using Hottel’s charts
8.07b Nonluminous radiation using equations
8.08a Predicting heat transfer in boiler furnaces
8.08b Design of radiant section for heat recovery application
8.09a Evaluating distribution of radiation to tube banks
8.09b Estimating the temperature of a lance inside boiler enclosure
8.11 Effect of gas velocity, tube size on fire tube boiler size
8.12 Computing heat flux, tube wall temperatures
8.13 Effect of scale formation on tube wall temperature and boiler perforMance
8.14 Design of water tube boilers
8.15a Predicting off-design performance
8.15b Logic for off-design performance evaluation for water tube boilers
8.16 Estimating metal temperature in a boiler superheater tube; thermal resistances in heat transfer; calculating heat flux
8.17 Predicting performance of fire tube and water tube boilers
8.18 Why finned tubes are used and their design aspects
8.19a Heat transfer and pressure drop in finned tubes using ESCOA correla
Tions
8.19b Heat transfer in finned tubes using Briggs and Young correlation
8.19c Predicting the performance of a finned tube superheater
8.20 Sizing of finned tube evaporator
8.21 Comparison of bare tube and finned tube boilers
8.22 In-line versus staggered arrangement
8.23 Effect of tube-side heat transfer on fin configuration
8.24 Effect of tube-side fouling on bare and finned tube boilers
8.25 Estimating weight of finned tubes
8.26 Effect of fin thickness and conductivity on boiler performance and tube and fin tip temperatures
8.27a Is surface area an important criterion for boiler selection?
8.27b Optimization of a finned evaporator surface
8.28 Design of tubular air heaters
8.29 Off-design performance of air heaters
8.30 Predicting performance of economizers using NTU method
8.31 Evaluating natural convection heat transfer coefficients in air
8.32 Natural convection heat transfer in liquids
8.33 Determining size of coil/tube bundle immersed in liquids
8.34 Evaluating gas/steam temperature profiles in HRSGs
8.35a Simulating off-design performance
8.35b A simplified approach to determining auxiliary fuel requirement in an
HRSG
8.36 Why gas exit temperature cannot be assumed in HRSGs
8.37 How to optimize temperature profiles in HRSGs
8.38 Efficiency of HRSGs according to ASME Power Test Code
8.39a Effect of fresh air fan size on HRSG performance
8.39b Performance of a multipressure HRSG in fresh air-fired mode
8.40 How to evaluate operating costs in HRSGs
8.41 Why economizer steaming occurs in gas turbine HRSGs
8.42 Why water tube boilers are preferred to fire tube boilers for gas turbine applications
8.43 Why 10% increase in surface area does not mean 10% more duty in boilers or heat transfer equipment
8.44a Time required to heat up boilers
8.44b Transient heating of a superheater bundle
8.44c Transient response of a water tube evaporator to cutoff in heat input and
Feedwater supply
8.44d Response of a water tube evaporator when steam demand increases and feedwater supply is cut off 8.45a Parameters to be considered in testing performance of HRSGs
8.45b Evaluating HRSG performance from operating data
8.46 Estimating boiling heat transfer coefficient and critical heat flux in water
Tube boilers
8.47a Relating heat flux, steam pressure, quality, flow in water tube boilers
8.47b Estimating critical heat flux in fire tube boilers
8.47c Estimating critical heat flux in a fire tube boiler; correcting for bundle
Geometry
8.48 Simplified approach to designing fire tube boilers
8.49 Simplified approach to designing water tube boilers
8.50 Estimating tube bundle size
8.51 Estimating thickness of insulation for flat and curved surfaces; effect of
Wind velocity; estimating thickness to limit surface temperatures
8.52 Estimating surface temperature of given thickness of insulation; trial- and-error procedure to determine casing temperature
8.53 Sizing insulation to prevent freezing; determining water dew point
8.54a Estimating heat loss from pipes for various insulation thicknesses
8.54b Estimating temperature drop of fluids in insulated piping
8.55 Optimum thickness of insulation; life-cycle costing; annual heat loss and capitalized cost; annual heat loss if no insulation is used
8.56 Design of hot casing
8.57 Temperature of duct or stack wall with and without insulation
8.58 Effect of wind velocity, casing emissivity on heat loss
8.59a Checking for noise and vibration problems in heat transfer equipment
8.59b Determining natural frequency of vibration of a tube bundle
8.59c Computing acoustic frequency
8.59d Determining vortex shedding frequency
8.59e Checking for bundle vibrations
8.59f Checks for tube bundle vibration using damping and fluid elastic instability criteria
8.60 Estimating specific heat, viscosity, and thermal conductivity for a gas mixture
8.61 Effect of gas analysis on heat transfer
8.62 Effect of gas pressure on heat transfer
8.63 Converting gas analysis from weight to volume basis
8.64 Effect of gas pressure and analysis on design of fire tube boiler
How is the surface area of heat transfer equipment determined? What terms can be neglected while evaluating the overall heat transfer coefficient in boilers, economizers, and superheaters?
The energy transferred in heat transfer equipment, Q, is given by the basic equation
Q = U x A x A T (1)
Also,
Wh Ahh = Wc Ahc (2)
Where
A = surface area, ft2 W = fluid flow, lb/h
Ah = change in enthalpy (subscripts h and c stand for hot and cold)
AT = corrected log-mean temperature difference, °F U = overall heat transfer coefficient, Btu/ft2h °F
For extended surfaces, U can be obtained from [1] 1 A A
U = h~At + ff ‘■x A + ff o+
At d, d 1
— x——- x In — H——
Aw 24Km dt zh0
Where
At = surface area of finned tube, ft2/ft A,- = tube inner surface area = %di/12, ft2/ft Aw = average wall surface area = p(d + d,)/24, ft2/ft Km = thermal conductivity of the tube wall, Btu/fth °F
D, d, = tube outer and inner diameter, in. ff,, ffo = fouling factors inside and outside the tubes, ft2h °F/Btu h,, ho = tube-side and gas-side coefficients, Btu/ft2h °F Z = fin effectiveness
If bare tubes are used instead of finned tubes, At = pd/12.
Equation (3) can be simplified to
1 d 1 d d
U = hd + ho+ 24k; x d
D (4)
+ ff, x d + ffo
Where ho is the outside coefficient.
Now let us take the various cases.
Water Tube Boilers, Economizers, and Superheaters
The gas-side heat transfer coefficient ho is significant; the other terms can be neglected. In a typical bare tube economizer, for example, h, = 1500 Btu/ft2 h °F, ff, and ffo = 0.001 ft2h °F/Btu, and ho = 12 Btu/ft2 h °F. d = 2.0 in., d, = 1.5 in., and Km = 25 Btu/fth °F.
Substituting into Eq. (4) yields
1 2.0 1 2.0 , 2
— ——————— 1—- 1———— x ln —
U 1500 x 1.5 12 24 x 25 1.5
+ 0.001 x 20 + 0.001 = 0.0874
Hence,
U = 11.44 Btu/ft2 h °F
Thus we see that the overall coefficient is close to the gas-side coefficient, which is the highest thermal resistance. The metal thermal resistance and the tube-side resistance are not high enough to change the resistance distribution much.
However, in a liquid-to-liquid heat exchanger, all the resistances will be of the same order, and hence none of the resistances can be neglected.
TOC o "1-5" h z Even if finned tubes were used in the case above, with At/A, = 9 substituted into Eq. (3), U = 9.3 Btu/ft2 h °F, which is close to ho. Thus, while trying to
Figure U for economizers, water tube boilers, or gas-to-liquid heat exchangers, U
May be written as
U = 0.8 to 0.9 x ho (5)
Ho is large, on the order of 1000-1500Btu/ft2h°F, whereas h, will be about 10- 12Btu/ft2h °F. Again, using Eq. (4), it can be shown that
U h x d (6)
All the other thermal resistances can be seen to be very small, and U approaches the tube-side coefficient h,.
Gas-to-Gas Heat Exchangers (Example: Air Heater in Boiler Plant)
In gas-to-gas heat transfer equipment, both hi and ho are small and comparable, while the other coefficients are high.
Assuming that ho = 10 and hi = 15, and using the tube configuration above,
1
|
-4 |
2.0 1
+ —- + 0.001 + 9.6 x 10
U 15 x 1.5 10
+ 0.001 x 15 = 0.1922
Or
U = 5.2 Btu/ft2 h °F
Simplifying Eq. (4), neglecting the metal resistance term and fouling, we obtain
H:d:/d , ,
U=hox hoiim (7)
Thus both ho and h, contribute to U.
AT, the corrected log-mean temperature difference, can be estimated from
AT — AT —
AT = FT x —ATmm_
Ln(ATmax/ATmin)
Where FT is the correction factor for flow arrangement. For counterflow cases, FT = 1.0. For other types of flow, textbooks may be referred to for FT. It varies from 0.6 to 0.95 [2]. ATmax and ATmin are the maximum and minimum terminal differences.
In a heat exchanger the hotter fluid enters at 1000°F and leaves at 400°F, while the colder fluid enters at 250°F and leaves at 450°F. Assuming counterflow, we have
ATmax = 1000 — 450 = 550°F ATmin = 400 — 250 = 150°F
Then
550 — 150
AT = mc55i07T50) = 307°F
How is the tube-side heat transfer coefficient ht estimated?
The widely used expression for ht is [1]
TOC o "1-5" h z Nu = 0.023 Re0 8 Pr0 4 (8)
Where the Nusselt number is
Nu = пЙ (9)
The Reynolds number is
Wd, , ,
Re = 15.2—, (10)
Where w is the flow in the tube in lb/h, and the Prandtl number is
Pr=mi (ii)
where
M = viscosity, lb/fth Cp = specific heat, Btu/lb °F k = thermal conductivity, Btu/fth °F
All estimated at the fluid bulk temperature.
Substituting Eqs. (9)-(11) into Eq. (8) and simplifying, we have
W°-8k°-6CS’4 w°-8C
Hi = 2’44 x d/V4 = 2’44 x "dp" (12)
Where C is a factor given by
|
-‘p |
K 0’6c0’4
|
M0’4 |
C = ■
C is available in the form of charts for various fluids [1] as a function of temperature. For air and flue gases, C may be taken from Table 8.1.
For hot water flowing inside tubes, Eq. (8) has been simplified and, for t < 300°F, can be written as [3]
V08
H, — = (150 + 1.550-^ (13)
Where
V = velocity, ft/s t = water temperature, °F
For very viscous fluids, Eq. (8) has to be corrected by the term involving viscosities at tube wall temperature and at bulk temperature [1].
Estimate h, when 200 lb/h of air at 800°F and atmospheric pressure flows in a tube of inner diameter 1.75 in.
|
Table 8.1 Factor C for Air and Flue Gases
|
Using Table 8.1 And Eq. (12), we have C = 0.187.
0 187
H = 2.44 x 2000 8 x ‘ ia = 11.55 Btu/f2 h °F ‘ 1.7518
Where
W = flow, lb/h
Dt = inner diameter, in.
For gases at high pressures, Ref. 1 gives the C values. (See also p. 531.)
In an economizer, 50,000 lb/h of water at an average temperature of 250°F flows in a pipe of inner diameter 2.9in. Estimate ht.
Let us use Eq. (13). First the velocity has to be calculated. From Q5.07a,
V = 0.05(wv/dt2). v, the specific volume of hot water at 250°F, is 0.017 cuft/lb. Then, t
|
V = 0.05 x 50,000 x -2-^ = 5.05 ft/s |
0.017
J00 x
Hence, from Eq. (13),
5 05°’8
H- = (150 + 1.55 x 250) x —= 1586 Btu/ft2 h °F
2’90’2
Estimate the heat transfer coefficient when 4000lb/h of superheated steam at 500psia and an average temperature of 750°F flows inside a tube of inner diameter 1.5in.
Using Table 8.2, we see that C = 0.318. From Eq (12)
Ht = 2.44 x 4000—X80 318 = 285 Btu/ft2 h °F 1.518
If steam were saturated, C = 0.383 and ht = 343 Btu/ft2 h°F.
|
Pressure (psia)
|
How is the outside gas heat transfer coefficient ho in boilers, air heaters, economizers, and superheaters determined?
The outside gas heat transfer coefficient ho is the sum of the convective heat transfer coefficient hc and nonluminous heat transfer coefficient.
Ho = hc + (14)
For finned tubes, ho should be corrected for fin effectiveness. is usually small
If the gas temperature is less than 800°F and can be neglected.
A conservative estimate of hc for flow of fluids over bare tubes in in-line and staggered arrangements is given by [1]
Nu = 0.33 Re0 6 Pr033 (15)
Substituting, we have the Reynolds, Nusselt, and Prandtl numbers
Re=(16)
Nu=M (17)
And
Pr = ^ (18)
K
Where
G = gas mass velocity, lb/ft2 h d = tube outer diameter, in. m = gas viscosity, lb/fth k = gas thermal conductivity, Btu/fth °F Cp = gas specific heat, Btu/lb °F
All the gas properties above are to be evaluated at the gas film temperature. Substituting Eqs. (16)-(18) into Eq. (15) and simplifying, we have
Hc = °.9G°’6 ^ (19)
Where
C0.33
F = k061 ^ (20)
Factor F has been computed for air and flue gases, and a good estimate is given in Table 8.3.
The gas mass velocity G is given by
W
G = 12 —————— (21)
NwL(St — d) v ;
Where
Nw = number of tubes wide ST = transverse pitch, in.
L = tube length, ft Wg = gas flow, lb/h
|
Table 8.3 F Factor for Air and Flue Gases
|
For quick estimates, gas film temperature f can be taken as the average of gas and fluid temperature inside the tubes.
Determine the gas-side convective heat transfer coefficient for a bare tube superheater tube of diameter 2.0 in. with the following parameters:
Gas flow = 150,000lb/h Gas temperature = 900°F Average steam temperature = 500°F Number of tubes wide =12 Length of the tubes = 10.5 ft Transverse pitch = 4.0 in.
Longitudinal pitch = 3.5in. (staggered)
Solution. Estimate G. From Eq. (21),
G =12 x -—»T9—r — = 7142 lb/ft2 h 12 x 10 . 5 x (4 — 2) ‘
Using Table 8.3, at a film temperature of 700°F, F = 0.113. Hence,
Hc = 0 . 9 x 71420 6 x 0143 = 15 . 8 Btu/ft2 h °F
Because the gas temperature is not high, the hN value will be low, so
U « ho « hc = 15 . 8 Btu/ft2 h °F
(Film temperature may be taken as the average of gas and steam temperatures, for preliminary estimates. If an accurate estimate is required, temperature drops across the various thermal resistances as discussed in Q8.16a must be determined.)
The convective heat transfer coefficient obtained by the above method or Grimson’s method can be modified to include the effect of angle of attack a of the gas flow over the tubes. The correction factor Fn is 1 for perpendicular flow and decreases as shown in Table 8.4 for other angles [1].
If, for example, hc = 15 and the angle of attack is 60°, then hc =
0. 94 x 15 = 14 .1 Btu/ft2 h °F.
|
Table 8.4 Correction Factor for Angle of Attack
|
8.05 Q:
How is the convective heat transfer coefficient for air and flue gases determined using Grimson’s correlation?
Grimson’s correlation, which is widely used for estimating hc [1], is
Nu = B x ReN (22)
Coefficient B and power N are given in Table 8.5.
150,0 lb/h of flue gases having an analysis (vol%) of CO2 = 12, H2O = 12, N2 = 70, and O2 = 6 flows over a tube bundle having 2 in. OD tubes at 4 in. square pitch. Tubes per row = 18; length = 10 ft. Determine hc if the fluid temperature is 353°F and average gas temperature is 700°F. The Appendix tables give the properties of gases.
At a film temperature of 0.5 x (353 + 700) = 526°F, Cp = 0.2695, m = 0.0642 and k = 0.02344. Then mass velocity G is
G = 12 x——— 150000———— = 5000 lb/ft2 h
18 x 10 x (4 — 2) ‘
|
Table 8.5 Grimson’s Values of B and N
|
5000 x 2
Re =—————— = 12,980
12 x 0.0642
H v 2
Nu = 0.229 x 12,980°•632 = 91 = ■ c
12 x 0.02344 or
2
Hc = 12 . 8 Btu/ft2 h °F
Compare in-line versus staggered arrangements of plain tubes from the point of View of heat transfer and pressure drop considerations. In a waste heat boiler
180,0 lb/h of flue gases at 880°F are cooled to 450°F generating steam at 150psig. The gas analysis is (vol%) CO2 = 7, H2O = 12, N2 = 75, and O2 = 6. Tube OD = 2 in.; tubes/row = 24; length = 7.5 ft. Compare the cases when tubes are arranged in in-line and staggered fashion with transverse pitch = 4 in. and longitudinal spacing varying from 1.5 to 3in.
Using Grimson’s correlation, the convective heat transfer coefficient hc was computed for the various cases. The nonluminous coefficient was neglected due to the low gas temperature. The surface area and the number of rows deep required were also computed along with gas pressure drop. The results are shown in Table 8.6.
Gas mass velocity G = „180 .00^X 12— = 6000 lb/ft2 h J 24 x (4 — 2) x 7 . 5
|
Table 8.6 In-Line Versus Staggered Arrangement of Bare Tubes
|
Average gas temperature = 0.5 x (880 + 450)/2 = 665°F, and film temperature is about 525°F.
Cp = 0.2706, m = 0.06479, k = 0.02367 at gas film temperature and Cp = 0.2753 at the average gas temperature.
6000 x 2 ,
Re =——————- = 15,434
12 x 0.06479
Duty Q = 180,000 x 0.99 x 0.2753 x (880 — 450) = 21 MMBtu/h Saturation temperature = 366°F.
(880 — 366) — (450 — 366)
AT = log-mean temperature difference = ■
Ln[(880 — 366)/(450 — 366)] = 237°F
With SL/d = 1.5 in-line, we have the values for B and N from Table 8.5:
B = 0.101 and N = 0.702 Hence
0.702 ——— ’ 2
Nu = 0.101 x 15,434 = 88.0 = hc x
12 x 0.02367
Or
Hc = 12.5
Because other resistances are small, U = 0.95hc = 11.87 Btu/ft2 h °F.
Hence
21 x 106
A = ———- —— = 7465 = 3.14 x 2 x 24 x 7.5Nd/12
237 x 11.87 d
Or the number of rows deep Nd = 79.
The friction factor f, using the method discussed in Q7.27, is
F = 15,434~°,15(0.044 + 0.08 x 1.5) = 0.0386
Average gas density = 0.0347 lb/ft3
_1(1 2 0.0386
Gas pressure drop = 9.3 x 10 10 x 60002 x 79 x————— = 2.95 in. WC
F F 0.0347
The calculations for the other cases are summarized in Table 8.6.
1. The staggered arrangement of bare tubes does not have a significant impact on the heat transfer coefficient when the longitudinal spacing exceeds 2, which is typical in steam generators. Ratios lower than 1.5 are not used, owing to potential fouling concerns or low ligament efficiency.
2. The gas pressure drop is much higher for the staggered arrangement. Hence, with bare tube boilers the in-line arrangement is preferred. However, with finned tubes, the staggered arrangement is comparable with the in-line and slightly better in a few cases. This is discussed later.
8.07a Q:
How is the nonluminous radiation heat transfer coefficient evaluated?
In engineering heat transfer equipment such as boilers, fired heaters, and process steam superheaters where gases at high temperatures transfer energy to fluid inside tubes, nonluminous heat transfer plays a significant role. During combustion of fossil fuels such as coal oil, or gas—triatomic gases—for example, water vapor, carbon dioxide, and sulfur dioxide—are formed, which contribute to radiation. The emissivity pattern of these gases has been studied by Hottel, and charts are available to predict gas emissivity if gas temperature, partial pressure of gases, and beam length are known.
Net interchange of radiation between gases and surroundings (e. g., a wall or tube bundle or a cavity) can be written as
|
|
(23)
Where
Sg = emissivity of gases at Tg
Ag = absorptivity at To
Tg = absolute temperature of gas, °R
To = absolute temperature of tube surface, °R
Sg is given by
|
(24) |
Sg = Sc + ZSw — As
Ag is calculated similarly at To. z is the correction factor for the water pressure, and As is the decrease in emissivity due to the presence of water vapor and carbon dioxide.
Although it is desirable to calculate heat flux by (23), it is tedious to estimate ag at temperature To. Considering the fact that T4 will be much smaller
Than Tg4, with a very small loss of accuracy we can use the following simplified equation, which lends itself to further manipulations.
|
(25) |
Q = SЈg(Tg — T) = hN (Tg — To)
The nonluminous heat transfer coefficient hN can be written as
(26)
To estimate hN, partial pressures of triatomic gases and beam length L are required. L is a characteristic dimension that depends on the shape of the enclosure. For a bundle of tubes interchanging radiation with gases, it can be shown that
|
|
(27a)
L is taken approximately as 3.4-3.6 times the volume of the space divided by the
Surface area of the heat-receiving surface. For a cavity of dimensions a, b and c,
|
1. 7 |
|
L = |
|
2(ab + bc + ca) 1/a + 1/b + 1/c |
|
3 . 4 x abc |
 |
|
|
|
In the case of fire tube boilers, L = di.
Sg can be estimated using Figs. 8.1a-8.1d, which give ec, ew, z, and As, respectively. For purposes of engineering estimates, radiation effects of SO2 can be taken as similar to those of CO2. Hence, partial pressures of CO2 and SO2 can be added and Fig. 8.1 used to get sc.
Determine the beam length L if ST = 5in., SL = 3.5 in., and d = 2 in.
Solution.
|
= 7.8 in. |
|
L = 1. 08 x |
5 x 3. 5 — 0 . 785 x 4
2
In a fired heater firing a waste gas, CO2 in flue gases = 12% and H2O = 16%. The gases flow over a bank of tubes in the convective section where tubes are arranged as in Example 1 (hence L = 7.8). Determine hN if tg = 1650°F and to = 600°F.
|
FIgure 8.1a Emissivity of carbon dioxide. (From Ref 1.) |
Solution.
7.8
TOC o "1-5" h z PcL = 0.12 x — = 0.078 atm ft c 12
7 8
PwL = 0.16 x — = 0.104 atm ft w 12
In Fig. 8.1a at Tg = (1650 + 460) = 2110°R and PcL = 0.078, sc = 0.065. In Fig. 8.1b, at Tg = 2110°R and PwL = 0.104, sw = 0.05. IN Fig. 8.1c, corresponding to (P + Pw)/2 = 1.16/2 = 0.58 and PwL = 0.104, z = 1.1. In Fig. 8.1d,
|
FIgure 8.1b Emissivity of water vapor. (From Ref 1.) |
Corresponding to Pw/(Pc + Pw) = 0 .16/0 . 28 and (Pc + Pw)L = 0 .182, As : 0.002. Hence,
Sg = 0.065 + (1.1 x 0.05) — 0.002 = 0.118
Using Eq. (26) with the Boltzmann constant a = 0 .173 x 10-8,
21104 — 10604
|
2110 — 1060 |
HN = 0 .173 x 10-8 x 0 .118 x ■ = 3. 6 Btu/ft2 h °F Thus, hN can be evaluated for gases.
|
FIgure 8.1c, d (c) Correction factor for emissivity of water vapor. (d) Correction term due to presence of water vapor and carbon dioxide. (From Ref 1.) |
8.07b Q:
Can gas emissivity be estimated using equations?
Gas emissivity can be obtained as follows. hN is given by Eq. (26),
T4- t
1 g o
HN = asg ————-
N g T ______ T
Tg To
Where
A = Stefan-Boltzmann constant = 0.173 x 10 8 Tg and To = gas and tube outer wall temperature, °R
Sg, gas emissivity, is obtained from Hottel’s charts or from the expression
Eg = 0.9 x (1 — e-KL) (28a)
(0.8 +1.6pw)x(1 — 0.38Tg/1000)
K =——————— u,—————- r x (Fc +Fw) (28b)
V(pc +pw)L
Tg is in K. L is the beam length in meters, and pc and pw are the partial pressures of carbon dioxide and water vapor in atm. L, the beam length, can be estimated for a tube bundle by Eq. (27a),
L =1.08 x ST xSL -°.785d2
D
ST and SL are the transverse pitch and longitudinal pitch. Methods of estimating pc and pw are given in Chapter 5.
In a boiler superheater with bare tubes, the average gas temperature is 1600°F and the tube metal temperature is 700°F. Tube size is 2.0 in., and transverse pitch ST = longitudinal pitch SL = 4.0 in. Partial pressures of water vapor and carbon dioxide are pw = 0.12, pc = 0.16. Determine the nonluminous heat transfer coefficient.
From Eq. (27a), the beam length L is calculated.
4 x 4 — 0:785 x 2 x 2
L = 1.08 x———————————
2
= 6.9 in. = 0.176 m
Using Eq. (28b) with Tg = (1600 — 32)/1.8 + 273 = 1114 K, we obtain
(0.8 + 1.6 x 0.12) x(1 — 0.38 x 1.114) A
K =——————— . —————- x 0.28
0:28 x 0:176
= 0:721 From Eq. (28a),
Sg = 0.9 x [1 — exp(-0.721 x 0.176)] = 0.107 Then, from Eq. (26),
8 20604 — 11604
HN = 0.173 x 0.107 x 10-8 x 1600 — 700 = 3.33 Btu/ft2 h °F
8.08a Q:
How is heat transfer in a boiler furnace evaluated?
Furnace heat transfer is a complex phenomenon, and a single formula or correlation cannot be prescribed for sizing furnaces of all types. Basically, it is an energy balance between two fluids—gas and a steam-water mixture. Heat transfer in a boiler furnace is predominantly radiation, partly due to the luminous part of the flame and partly due to nonluminous gases. A general approximate expression can be written for furnace absorption using an energy approach:
Qf = ApSw Sf s(Tg — To4)
= Wf LHV — Wghe )
Gas temperature (Tg) is defined in many ways; some authors define it as the exit gas temperature itself. Some put it as the mean of the theoretical flame temperature and te. However, plant experience shows that better agreement between measured and calculated values prevails when tg = tc + 300 to 400°F [1]. The emissivity of a gaseous flame is evaluated as follows [1]:
Sf = p(1 — e-KPL) (30)
P characterizes flame-filling volumes.
P = 1.0 for nonluminous flames = 0.75 for luminous sooty flames of liquid fuels = 0.65 for luminous and semiluminous flames of solid fuels L = beam length, m
К = attenuation factor, which depends on fuel type and presence of ash and its concentration. For a nonluminous flame it is
K = 0-8 + (1 — 0.38Te/1000) (pc + pw) (28b)
V(pc + pw)L
For a semiluminous flame, the ash particle size and concentration enter into the calculation:
0 :8 + 1 :6pw
K = , (1 — 0.38Te/1000) (pc + pw)
V(pc + pw)L
1 ‘/3
Where
Dm = the mean effective diameter of ash particles, in mm dm = 13 for coals ground in ball mills
= 16 for coals ground in medium — and high-speed mills = 20 for combustion of coals milled in hammer mills m = ash concentration in g/N m3 Te = furnace exit temperature, K
For a luminous oil or gas flame,
K=їж — 05 <28d>
Pw and pc are partial pressures of water vapor and carbon dioxide in the flue gas.
The above equations give only a trend. A wide variation could exist due to the basic combustion phenomenon itself. Again, the flame does not fill the furnace fully. Unfilled portions are subjected to gas radiation only, the emissivity of which (0.15-0.30) is far below that of the flame. Hence, decreases. Godridge reports that in a pulverized coal-fired boiler, emissivity varied as follows with respect to location [3]:
TOC o "1-5" h z Excess air 15% 25%
Furnace exit 0.6 0.5
Middle 0.7 0.6
Also, furnace tubes coated with ferric oxide have emissivities, sw, of the order of
0. 8, depending on whether a slag layer covers them. Soot blowing changes sw considerably. Thus, only an estimate of Sf and sw can be obtained, which varies with type of unit, fuel, and operation regimes.
To illustrate these concepts, a few examples are worked out. The purpose is only to show the effect of variables like excess air and heat release rates on furnace absorption and furnace exit gas temperature.
Determine the approximate furnace exit gas temperature of a boiler when net heat input is about 2000 x 106Btu/h, of which 1750 x 106Btu/h is due to fuel and the rest is due to air. HHV and LHV of coals fired are 10,000 and 9000 Btu/lb, respectively, and a furnace heat release rate of 80,000 Btu/ft2h (projected area basis) has been used. The values sw and Sf may be taken as 0.6 and 0.5, respectively; 25% is the excess air used. Water-wall outer temperature is 600°F. Ash content in coal is 10%.
Solution.
Q LHV
Q = 80,000 = Wf ——
Ap f Ap
From combustion calculation methods discussed in Chapter 5, using 1 MMBtu fired basis, we have the following ratio of flue gas to fuel:
Wg 760 x 1.24 x 104 | 1 10
Wf = 10 + 1 — 100
= 10.4 lb/lb
Q = APSwSf s (Tg — T4) = Wf LHV — Wghe
Dividing throughout by Wf gives A
Wf SwSf S(Tg — T) = LHV — W/e
Ap/Wf = LHV/80,000 = 0.1125
Assume te = 1900°F. Then
Cpm = 0.3 Btu/lb °F
Tg = 1900 + 300 = 2200° F = 2660°R
Let us see if the assumed te is correct. Substituting for Ap /Wf, sw, Sf, s, Tg, Te in the above equation, we have (LHS = left-hand side; RHS = right-hand side)
LHS = 0.1125 x 0.6 x 0.5 x 0.173 x (26.64 — 10.64) = 2850 RHS = (9000 — 10.4 x 1900 x 0.3) = 3072
These do not tally, so we try te = 1920°F. Neglect the effect of variation in Cpm:
LHS = 0.1125 x 0.6 x 0.5 x (26.84 — 10.64) x 0.173 = 2938 RHS = 9000 — 1920 x 0.3 x 10.4 = 3009
These agree closely, so furnace exit gas temperature is around 1920°F. Note that the effect of external radiation to superheaters has been neglected in the energy balance. This may give rise to an error of 1.5-2.5% in te, but its omission greatly simplifies the calculation procedure. Also, losses occurring in the furnace were omitted to simplify the procedure. The error introduced is quite low.
It is desired to use a heat loading of 100,000 Btu/ft2 h in the furnace in Example
1. Other factors such as excess air and emissivities remain unaltered. Estimate the furnace exit gas temperature.
Solution.
Q LHV
Q = 100,000 = wf ——
Ap f Ap
Al = ^HV_ = 0.09
Wf 100,000
W„
= 10.4, te = 2000°F; tg = 2300°F
Wf g
Cpm = 0.3 Btu/lb °F; Tg = 2300 + 460 = 2760°R LHS = 0.09 x 0.6 x 0.5 x 0.173 x (27.64 — 10.64) = 2664 RHS = (9000 — 10.4 x 2000 x 0.3) = 2760
From this it is seen that te will be higher than assumed. Let te = 2030°F, Tg = 2790°R
Then
LHS = 0.09 x 0.6 x 0.5 x 0.173
X [(27.9)4 — (10.6)4] = 2771 RHS = 9000 — 10.4 x 2030 x 0.3 = 2667
Hence, te will lie between 2000 and 2030°F, perhaps 2015°F.
The exercise shows that the exit gas temperature in any steam generator will increase as more heat input is given to it; that is, the higher the load of the boiler, the higher the exit gas temperature. Example 3 shows the effect of excess air on
Te-
What will be the furnace exit gas temperature when 40% excess air is used instead of 25%, heat loading remaining at about 100,000 Btu/ft2h in the furnace mentioned in earlier examples?
Solution.
Q LHV Ap
Q = 100,000 = Wf ——, — p = 0.09
Ap f Ap Wf
Wg 760 x 1.4 x 104
W =———— 106——- + 09 = 1L54lb/lb
Te = 1950°F, Cpm = 0.3 Btu/lb °F
Tg = 1950 + 300 + 460 = 2710°R
LHS = 0.09 x 0.6 x 0.5 x 0.173
X [(27.1)4 — (10.6)4] = 2460 RHS = 9000 — (11.54 x 1950 x 0.3) = 2249
These nearly tally; hence, te is about 1950°F, compared to about 2030°F in Example 2. The effect of the higher excess air has been to lower te.
If ew x Јf = 0.5 instead of 0.3, what will be the effect on te when heat loading is
100,0 Btu/ft2h and excess air is 40%?
Solution. Let
Te = 1800°F; Tg = 1800 + 300 + 460 = 2560°R LHS = 0.09 x 0.5 x 0.173 x [(25.6)4 — (10.6)4]
= 3245
RHS = 9000 — (11.54 x 1800 x 0.3) = 2768
Try
Te = 1700°F; Tg = 2460°R
LHS = 0.09 x 0.5 x 0.173 x [(24.6)4 — (10.6)4]
= 2752
RHS = 9000 — (11.54 x 1700 x 0.3) = 3115
Try
Te = 1770°F; Tg = 2530°R
Then
LHS = 3091; RHS = 2872
Hence, te will be around 1760°F. This example shows that when surfaces are cleaner and capable of absorbing more radiation, te decreases.
In practice, furnace heat transfer is not evaluated as simply as shown above Because of the inadequacy of accurate data on soot emissivity, particle size, distribution, flame size, excess air, presence and effect of ash particles, etc. Hence, designers develop data based on field tests. Estimating te is the starting point for the design of superheaters, reheaters, and economizers.
Some boiler furnaces are equipped with tilting tangential burners, whereas some furnaces have only front or rear nontiltable wall burners. The location of the burners affects te significantly. Hence, in these situations, correlations with practical site data would help in establishing furnace absorption and temperature profiles. (See also p. 112, Chapter 3.)
A promising technique for predicting furnace heat transfer performance is the zone method of analysis. It is assumed that the pattern of fluid flow, chemical heat release, and radiating gas concentration are known, and equations describing conservation of energy within the furnace are developed. The furnace is divided into many zones, and radiation exchange calculations are carried out.
How is heat transfer evaluated in unfired furnaces?
Radiant sections using partially or fully water-cooled membrane wall designs are used to cool gas streams at high gas temperatures (Fig. 8.2). They generate saturated steam and may operate in parallel with convective evaporators if any. The design procedure is simple and may involve an iteration or two. The higher the partial pressures of triatomic gases, the higher will be the nonluminous radiation and hence the duty.
|
Figure 8.2 Radiant furnace in a water tube boiler. |
If a burner is used as in the radiant section of a furnace-fired HRSG, the emissivity of the flame must also be considered. As explained elsewhere [8], radiant sections are necessary to cool the gases to below the softening points of any eutectics present so as to avoid bridging or slagging at the convection section. They are also required to cool gases to a reasonable temperature at the superheater if it is used.
200,0 lb/h of flue gases at 1800°F has to be cooled to 1600°F in a radiant section of a waste heat boiler of cross section 9 ft x 11 ft. Saturated steam at 200 psig is generated. Determine the furnace length required. Flue gas analysis is (vol%) CO2 = 8, H2O = 18, N2 = 72, O2 = 2. Assume a length of 25 ft and that the furnace is completely water-cooled.
Surface area for cooling = (11 + 9)x2 x 25 = 1000 ft volume
Beam length = 3.4 x
Surface area
9 x 11 x 25
= 3.4 x———————————————— = 7.1 ft = 2.15 m
2 x (11 x 9 + 9 x 25 + 11 x 25)
Average gas temperature = 1700°F = 1200 K. Partial pressure of CO2 = 0.08, and that of H2O = 0.18. Using Eq. (28b),
|
|
K = (0.8 + 1.6 x 0.18)(1 — 0.38 x 1.2) x
Gas emissivity sg = 0.9 x (1 — e-0’2053 x 2 16) = 0.32 23
Let the average surface temperature of the furnace be 420°F (saturation temperature plus a margin). Then the energy transferred is
Qr = 0.173 x 0.9 x 0.3223 x (21.64 — 8.84) x 1000 = 10.63 MM Btu/h
Required duty = 200,000 x 0.99 x 0.32 x 200 = 12.67 MM btu/h
Where 0.32 is the gas specific heat. Hence the furnace should be longer. The beam length and hence the gAs emissivity will not change much with change in furnace length; therefore one may assume that the furnace length required = (12.67/10.63) x 25 = 29.8 or 30 ft.
If the performances at other gas conditions are required, a trial-and-error procedure is warranted. First the exit gas temperature is assumed; then the energy transferred is computed as shown above and compared with the assumed duty.
How is the distribution of external radiation to tube bundles evaluated? Discuss the effect of tube spacing.
Tube banks are exposed to direct or external radiation from flames, cavities, etc., in boilers. Depending on the tube pitch, the energy absorbed by each row of tubes varies, with the first row facing the radiation zone receiving the maximum energy. It is necessary to compute the energy absorbed by each row, particularly in superheaters, because the contribution of the radiation can result in high tube wall temperatures.
The following formula predicts the radiation to the tubes [8].
(31)
Where a is the fraction of energy absorbed by the first row. The second row would then absorb (1 — a)a; the third row, {1 — [a + (1 — a)a]}a; and so on.
1 MM Btu/h of energy from a cavity is radiated to a superheater tube bank that has 2 in. OD tubes at a pitch of 8 in. If there are six rows, estimate the distribution of energy to each row.
Solution. Substituting d = 2, S = 8 into Eq. (31), we have
|
2/8 2 |
|
A = 3.14 |
Sin 1 ( + p4 x 4 — 1 — 2
28
= 0.3925 — 0.25(0.2526 + VT5 — 4) = 0.361
Hence the first row absorbs 0.361 MM Btu/h.
The second row would receive (1 — 0.361) x 0.361 = 0.231 or 0.231 MM Btu/h.
The third row receives [1 — (0.361 + 0.231)] x 0.361 = 0.147 MM Btu/h.
The fourth row, [1 — (0.361 + 0.231 + 0.147)] x 0.361 = 0.094 MM Btu/h, and so on.
It can be seen that the first row receives the maximum energy and the amount lessens as the number of rows increases. For a tube pitch S of 4 in., a = 0.6575. The first row receives 0.6575 MM Btu/h; the second, 0.225 M Btu/h; and the third, 0.077 MM Btu/h. Hence if the tube pitch is small, a large amount of energy is absorbed within the first two to three rows, resulting in high heat flux in those tubes and consequently high tube wall temperatures. Hence it is better to use a wide pitch when the external radiation is large so that the radiation is spread over more tubes and the intensity is not concentrated within two or three tubes. Screen tubes in boilers and fired heaters perform this function.
A soot blower lance is inserted in a boiler convection section where hot flue gases at 2000°F are flowing around the tubes. If the water wall enclosure is at 400°F, what will be the lance temperature? Assume that the heat transfer coefficient between the flue gas and the lance is 15Btu/ft2h °F and the emissivity of the lance and the water wall tubes is 0.9.
The energy transferred between the flue gases and lance and from the lance to the water wall enclosure in Btu/ft2 h is given by
Q = hc(2000 — T)
= 0.173 x 0.9 x 0.9 x [(T + 460)4 — (400 + 460)4] x 10-8
Where
T = lance temperature, °F
0.173 x 10- 8 is the radiation constant
Emissivity of lance and enclosure = 0.9
Actually, a trial-and-error procedure is required to solve the above equation. However, it may be shown that at T = 1250°F, both sides balance and Q = 11,250 BtU/ft2 h. At low loads, when hc = 5 and with other parameters remaining the same, what will be the lance temperature? It can be shown to be about 970°F and Q = 5150btu/ft2h.
Hence just as a thermocouple reads a lower temperature due to the radiation to the enclosure, the lance also will not reach the gas temperature. Its temperature will be lower than that of the gas.
Determine the size of a fire tube waste heat boiler required to cool 100,000 lb/h of flue gases from 1500°F to 500°F. Gas analysis is (vol%) CO2 = 12, H2O = 12, N2 = 70, and O2 = 6; gas pressure is 5in. WC. Steam pressure is 150psig, and feedwater enters at 220°F. Tubes used are in 2 in. OD x 1.77 in. ID; fouling factors are gas-side fouling factor (ft); 0.002 ft2 h °F/Btu and steam-side ff = 0.001 ft2h°F/Btu. Tube metal thermal conductivity = 25Btu/fth°F. Steam — side boiling heat transfer coefficient = 2000 Btu/ft2 °F. Assume that heat losses and margin = 2% and blowdown = 5%.
Use Eq. (4) to compute the overall heat transfer coefficient, and then arrive at the size from Eq. (1).
Hdo/d), _L
24Km h0
Hi, the tube-side coefficient, is actually the sum of a convective portion hc plus a nonluminous coefficient hn. hc is obtained from Q8.04:
C
Hc = 2.44 x w08 x —r-T c d/’8
At the average gas temperature of 1000°F, the gas properties can be shown to be Cp = 0.287 Btu/lb °F, m = 0.084 lb/fth, and k = 0.0322 Btu/fth °F. Hence,
C = x (0.0322)0-6 = 0.208
.084/ v ’
Boiler duty Q = 100,000 x 0.98 x 0.287 x (1500 — 500)
= 28.13 x 106 Btu/h
Enthalpies of saturated steam, saturated water, and feedwater from steam tables are 1195.5, 338, and 188 Btu/lb, respectively. The enthalpy absorbed by steam is then (1195.5 — 188) + 0.05 x (338 — 188) = 1015Btu/lb, where 0.05 is the blowdown factor corresponding to 5% blowdown.
Hence,
28:13 106 ……………….
Steam generation =—————— = 27,710 lb/h
In order to compute ht, the flow per tube w is required. Typically w ranges from 100 to 200lb/h for a 2 in. tube. Let us start with 600 tubes; hence w = 100,000/600 = 167 lb/h.
1670:8
Hc = 2.44 x 0.208 x———— ^ = 10.9 Btu/ft2 h °F
C (1.77)
The nonluminous coefficient is usually small in fire tube boilers because the beam length corresponds to the tube inner diameter. However, the procedure used in Q8.07 can also be used here. Let us assume that it is 0.45 Btu/ft2h °F. Then
Ht = 10.90 + 0.45 = 11.35 Btu/ft2 h °F
Let us compute U. Because it is based on tube outside surface, let us call it U0.
1 2/1 77 2
W0 = iL^T + °-°01 + 0.002 x 177
+ ^(177) x 24xx25 + 0.0005
= 0.10 + 0.001 + 0.00226 + 0.00041 + 0.0005 = 0 .10417
Hence, U0 = 9.6 Btu/ft2 h °F.
The various resistances in ft2h °F/Btu are
|
Gas-side heat transfer |
0.10 |
|
Gas-side fouling |
0.00226 |
|
Metal resistance |
0.00041 |
|
Steam-side fouling |
0.001 |
|
Steam-side heat transfer |
0.0005 |
If U is computed on the basis of tube inner surface area, then U is given by the expression
Ai x Ui = Ao x Uo
Hence,
U = 9 . 6 x — = 10 . 85 Btu/ft2 h °F
I 1. 77 ‘
Log-mean temperature difference is
(1500 — 366) — (500 — 366) _ ln[(1500 — 366)/(500 — 366)]
Hence
Ao = 28 J3 x 106 = 6261 ft2
0 468 x 9. 6
= 3 .14 x 2 x 600 x —
12
So required length L of the tubes = 19.93 ft. Use 20 ft. Then
20 2 A0 = 3 .14 x 2 x 600 x — = 6280 ft2
0 12
Ai 5558 ft2
Let us compute the gas pressure drop using Eq. (12) of Chapter 7.
DPg = 93 x 10~6 x w2/Le-j5
Friction factor f depends on tube inner diameter and can be taken as 0.02. The equivalent length Le can be approximated by L + 5dt to include the tube inlet and exit losses.
Specific volume v obtained as 1/density, or v = 1/p. Gas density at the average gas temperature of 1000°F is pg = 39/1460 = 0.0267 lb/cu ft. Therefore,
DPg = 93 x 10~6 x 1672 x 0.02
X 20 + 5 xL775 = 3.23 in. WC
0. 0267 x (1.77)5
This is only one design. Several variables such as tube size and mass flow could be changed to arrive at several options that could be reviewed for optimum operating anD iNstalled costs.
8.11 Q:
What is the effect of tube size and gas velocity on boiler size? Is surface area the sole criterion for boiler selection?
Surface area should not be used as the sole criterion for selecting or purchasing boilers, because tube size and gas velocity affect this variable.
Shown in Table 8.7 are the design options for the same boiler duty using different gas velocities and tube sizes; the procedure described in Q8.10 was used to arrive at these options. The purpose behind this example is to bring out the fact that surface area can vary by as much as 50% for the same duty.
1. As the gas velocity increases, the surface area required decreases, which is obvious.
2. The smaller the tubes, the higher the heat transfer coefficient for the same gas velocity, which also decreases the surface area.
3. For the same gas pressure drop, the tube length is smaller if the tube size is smaller. This fact helps when we try to fit a boiler into a small space.
4. For the same tube size, increasing the gas velocity results in a longer boiler, a greater gas pressure drop, but smaller surface area.
In the case of water tube boilers, more variables such as tube spacing and in-line or staggered arrangement in addition to gas velocity and tube size can affect surface area. This is discussed elsewhere.
|
Tube size |
1.75 x 1.521 |
2 x 1.773 |
2.5 x 2.238 |
||||||
|
Velocity, ft/s |
109 |
141 |
166 |
110 |
140 |
165 |
109 |
140 |
166 |
|
Tubes |
1100 |
850 |
725 |
800 |
630 |
535 |
510 |
395 |
335 |
|
Length, ft |
19 |
20 |
21 |
22.5 |
24 |
25 |
29.5 |
31.5 |
33 |
|
Surface area, ft2 |
8318 |
6766 |
6059 |
8351 |
7015 |
6205 |
8811 |
7286 |
6474 |
|
U, Btu/ft2 h °F |
9.74 |
11.78 |
13.25 |
9.6 |
11.43 |
12.89 |
9.15 |
11.02 |
12.43 |
|
Pressure drop in. WC |
2.5 |
4.4 |
6.3 |
2.6 |
4.4 |
6.2 |
2.5 |
4.3 |
6.2 |
Gas flow = 110,000lb/h; inlet temperature = 1450°F; exit temperature = 500°F; steam pressure = 300psig; feedwater in = 230°F; blowdown = 5%; steam = 28,950 lb/h; gas analysis (vol%): CO2 = 7, H2O = 12, N2 = 75, O2 = 6; boiler duty = 29.4 MM Btu/h.
How is the tube wall temperature in fire tube boilers evaluated? Discuss the importance of heat flux.
To compute the tube wall temperatures, heat flux must be known. qo = heat flux outside tubes = Uo x (tg — t,) Btu/ft2 h
Similarly, qt (heat flux inside the tube) would be U x (tg — t,). However, heat flux outside the tubes is relevant in fire tube boilers because boiling occurs outside the tubes, whereas in water tube boilers the heat flux inside the tubes would be relevant. A high heat flux can result in a condition called departure from nucleate boiling (DNB), which will result in overheating of the tubes. It is preferable to keep the actual maximum heat flux below the critical heat flux, which varies from 150,000 to 250,000 Btu/ft2 h depending on steam quality, pressure, and tube condition [1].
An electrical analogy can be used in determining the tube wall temperatures. Heat flux is analogous to current, electrical resistance to thermal resistance, and voltage drop to temperature drop. Using the example worked in Q8.10, we have that at average gas conditions the product of current (heat flux) and resistance (thermal resistance) gives the voltage drop (temperature drop):
Qo = heat flux = 9.6 x (1000 — 366) = 6086 Btu/ft2 h
Temperature drop across gas film = 6086 x 0:1 = 609°F Temperature drop across gas-side fouling = 6086 x 0.00226 = 14°F Temperature drop across tube wall = 6086 x 0:00041 = 3°F Temperature drop across steam-side fouling = 6086 x 0:001 = 6°F Temperature drop across steam film = 6085 x 0:0005 = 3°F
Hence,
Average inside tube wall temperature = 1000 — 609 — 14 = 377°F Outside tube wall temperature = 377 — 3 = 347°F.
The same results are obtained working from the steam side.
Outside tube wall temperature = 366 + 6 + 3 = 375°F
One can also compute the maximum tube wall temperature by obtaining the heat flux at the hot gas inlet end.
8.13 Q:
What is the effect of scale formation on tube wall temperatures?
If nonsoluble salts such as calcium or magnesium salts or silica are present in the feedwater, they can deposit in a thin layer on tube surfaces during evaporation, thereby resulting in higher tube wall temperatures.
Table 8.8 lists the thermal conductivity k of a few scales. Outside fouling factor ff0 can be obtained if the scale information is available.
Thickness of scale
Ff =—————————
O conductivity
Let us use the same example as in Q8.10 and check the effect of ff0 on boiler duty and tube wall temperatures. Let a silicate scale of thickness 0.03 in. be formed. Then,
Ff0 = M3 = 0.05 ft2 h °F/Btu
0.6
|
Table 8.8 Thermal Conductivities of Scale Materials
|
Assume that other resistances have not changed. (Because of different duty and gas temperature profile, the gas-side heat transfer coefficient will be slightly different. However, for the sake of illustration, we neglect this.) We have
-L = 0.10 + 0.00226 + 0.00041 + 0.05 + 0.0005
Uo
= 0.15317
Hence, Uo = 6.52 Btu/ft2 h °F
Heat flux qo = 6.52 x (1000 — 366) = 4133 Btu/ft2 h
Temperature drop across outside steam film = 0:0005 x 4133
= 2°F
Temperature drop across steam-side fouling layer or scale = 4133 x 0:05
= 207°F
Temperature drop across tube wall = 4133 x 0.00041
= 2°F
We see that average tube wall temperature has risen to 366 + 2 + 207 + 2 = 577°F from an earlier value of about 375°F. Scale formation is a serious problem. Note that the heat flux is now lower, but that does not help. At the front end, where the heat flux is higher, the tubes would be much hotter.
Now let us check the effect on boiler duty. It can be shown [1,8] that
Ln sat = ——— UA (32)
Tg2 tsat Wg x CP x hlf
Where hlf is the heat loss factor. If 2% losses are assumed, then hlf = 0.98.
We know that Uo = 6.52, Ao = 6280, tg1 = 1500, tsat = 366. Hence,
1500 — 366 6.52 x 6280
Ln-
Tg2 — 366 100,000 x 0.98 x 0.287
= 1.456
Or
1500 — 366 = 4.29 tg2 — 366
Hence tg2 = 630°F compared to 500°F earlier. The reason for tg2 going up is the lower Uo caused by scale formation.
Hence new duty = 100,000 x 0.98 x 0.287 x (1500 — 630) = 24.47 x 106 Btu/h. The decrease in duty is 28.13 — 24.47 = 3.66MMBtu/h. Even assuming
A modest energy cost of $3/MM Btu, the annual loss due to increased fouling is 3.66 x 3 x 8000 = $87,800. The steam production in turn gets reduced.
Plant engineers should check the performance of their heat transfer equipment periodically to see if the exit gas temperature rises for the same inlet gas flow and temperature. If it does, then it is likely due to fouling on either the gas or steam side, which can be checked. Fouling on the gas side affects only the duty and steam production, but fouling on the steam side increases the tube wall temperature in addition to reducing the duty and steam production.
To ensure that variations in exit gas temperature are not due to fouling but are due to changes in gas flow or temperature, one can use simulation methods. For example, if, for the same gas flow, the inlet gas temperature is 1800°F, we can expect the exit gas temperature to rise. Under clean conditions, this can be estimated using the equation (32)
1500 — 366 1800 — 366
————— =—————— , or tg2 = 535 F
500 — 366 tG2 — 366 g2
Now if, in operation, the exit gas temperature were 570-600°F, then fouling could be suspected; but if the gas temperature were only about 535°F, this would only be due to the increased gas inlet temperature. Similarly, one can consider the effect of gas flow and saturation temperature.
How is the size of a water tube boiler determined?
The starting point in the design of an evaporator (Fig. 8.3) is the estimation of the overall heat transfer coefficient U. The cross-sectional data such as the number of tubes wide, spacing, and length of tubes are assumed. From the duty and log — mean temperature difference, the surface area is obtained. Then the number of rows deep is estimated. Tube wall temperature calculations and gas pressure drop evaluation then follow. A computer program is recommended to perform these tedious calculations, particularly if several alternatives have to be evaluated.
200,0 lb/h of clean flue gas from an incinerator must be cooled from 1100°F to 600°F in a bare tube evaporator. Steam pressure = 250psig saturated. Feedwater temperature = 230°F. Blowdown = 5%. Fouling factors on steam — and gas-side = 0.001 ft2 h°F/Btu. Gas analysis (vol%): CO2 = 7, H2O = 12, N2 = 75,
O2 = 6. Let heat loss from casing = 1%.
|
FIgure 8.3 Boiler evaporator bundle. |
S0luti0n: Use 2 x 1.773 in carbon steel tubes; number wide = 24; length = 10 ft; tube spacing = 4 in. square.
Average gas temperature = 0.5 x (1100 + 600) = 850°F
Steam temperature inside tubes = 406°F. Assume tube wall temperature = 410°F (this should be checked again later).
Film temperature = 0.5 x (850 + 410) = 630°F
Gas properties at film temperature are (from Appendix) Cp = 0.2741, m = 0.0693, k = 0.0255
Cp at average gas temperature = 0.282
Duty Q = 200,000 x 0.99 x 0.282 x (1100 — 600) = 27.92 MMBtu/h Steam enthalpy change = (1201.7 — 199) + 0.05 x (381.4 — 199) = 1011.82 Btu/lb
Hence
Steam generation = 27.92 x = 27,600 lb/h
6 1011.82 ‘
Gas mass velocity G = —200,000 x 12 = 4167 lb/ft[2] h
24 x 12 x (4 — 2)
4167 x 2
Reynolds number Re = Gd/12m = ——— ^ = 10,021
J 12 x 0.0693
Using Grimson’s correlation,
Nu = 0.229 x (10,021)0 632 = 77.3 The convective heat transfer coefficient
Hc = Nu x 12k = 77.3 x 12 x 00255 = 11.83 Btu/ft2 h °F d 2
Let us compute the nonluminous heat transfer coefficient hN. Partial pressures of CO2 and H2O are 0.06 and 0.12, respectively; beam length L = 1.08 x (4 x 4 — 0.785 x 4)/2 = 6.95 in. = 0.176 m.
Average gas temperature = 850°F = 727 K
Using Eq. (28b),
^ (0.8 + 1.6 x 0.12) x(1 — 0.38 x 0.727) x 0.19 ^
K =—————————————- jrr———————— = 0.746
(0.19 x 0.176)
Gas emissivity eg = 0.9 x (1 — e-0’746×0 176) = 0.1107 Assuming that the tube wall is at 420°F (to be checked later)
13 14 8 8[3]
HN = 0.173 x 0. 9 x 0.1107 x —————— — = 0.94 Btu/ft2 h °F
N 1310 — 880 ‘
Using a conservative boiling heat transfer coefficient of 2000 Btu/ft2 h and a tube thermal conductivity of 25 Btu/ft h °F; we have
Or
(1100 — 406) — (600 — 406)
Log-mean temperature difference = —————————————— — —
5 F ln[(1100 — 406)/(600 — 406)]
= 393°F
27 92 x 106 2
Surface area required A = —; = 5776 ft
4 12 . 3 x 393
A = 3.14 x 2 x Nd x 24 x 12/12 = 5776, or Nd = 38 . 4
Use 40 rows deep. Surface provided = 6016 ft2. Let us estimate the gas pressure drop.
28 2 492
Gas density p =———- ^————— = 0 . 0295 lb/ft
* F 359 x (460 + 850) ‘
Friction factor f = 10,020-a15 x (0.044 + 0.08 x 2) = 0.0512
2 0.0512
AP„ = 9 . 3 x 10-10 x 41672 x 40 x—————- = 1.12 in. WC
G 0.0295
The average heat flux on tube ID basis is
Q = 12.3 x (850 — 406) x 2/1.773 = 6160 Btu/ft2 h
Temperature drop across inside fouling layer = 6160 x 0.001 = 62°F Temperature drop across inside film coefficient = 6160/2000 = 3.1 °F Drop across tube wall = 0.0004 x 1.773 x 6160/2 = 2.2°F
Hence tube outer wall temperature = 406 + 6.2 + 3.1 + 2.2 = 418°F. Since this is close to the assumed value another iteration is not necessary.
Note that this is only the average tube wall temperature. The maximum heat flux is at the gas inlet, and one has to redo these calculations to obtain the maximum tube wall temperature. A computer program would help speed up these calculations.
8.15a
Q:
How is the off-design performance of a boiler evaluated? Predict the performance of the boiler designed earlier under the following conditions: Gas flow =
230,0 lb/h; gas inlet temperature = 1050°F; steam pressure = 200psig. Gas analysis remains the same.
Performance calculations are more involved than design calculations, because we do not know the gas exit temperature. The NTU method discussed in Q8.30 minimizes the number of iterations. However, for an evaporator, a simple procedure exists for predicting the performance.
The boiler duty Q is given by the expression
Q = WgCp(t1 — t2) = UA(tf~ <2) (33)
Ln[(t1 — ts)/(t2 — ts)]
Where
Ti, t2 = gas inlet and exit temperatures, °F ts = saturation temperature, °F Wg = gas flow, lb/h (correcting for heat loss factor)
Cp = gas specific heat at average gas temperature, Btu/lb °F U = overall heat transfer coefficient, Btu/ft2h °F A = surface area, ft2
Simplifying, we have
T!—s = _^L (34)
T2 — ts WgCp ‘ ’
First we have to estimate U. Assuming 580°F as the gas exit temperature, average gas temperature = 815°F and average film temperature = 613°F.
M = 0.06875, k = 0.0252, Cp = 0.2735 Cp at average gas temperature = 0.28 Btu/lb °F
12 2
G = 230,000 x ——- —- = 4791 lb/ft2 h
24 x 12 x 2
4791 x 2
Re =——————— = 11,615
12 x 0.06875
Nu = 0.229 x 11, 6150 632 = 84.9
Or
Hc = 84.8 x 12 x 0.0252/2 = 12.9 Btu/ft2 h °F
The nonluminous heat transfer coefficient may be computed as before and shown to be 0.895 Btu/ft2 h °F.
1 = 1/(0.895 + 12.9) + 0.001 + 0.0011 + 0.000565 + 0.0004 = 0.0756
U = 13.2 Btu/ft2 h °F
Using Eq. (34) with saturation temperature of 388°F, we have 1050 — 388 13.2 x 6016 1 5
T2 — 388 = 230,000 x 0.99 x 0.28 = .
Or
T2 = 578°F From eq. (32)
Q = 230,000 x 0.99 x 0.28 x (1050 — 578) = 30.0 MM Btu/h
Steam generation = 29,770 lb/h
The tube wall temperature and gas pressure drop may be computed as before. It may be shown that the gas pressure drop is 1.5 in. WC and the tube wall temperature is 408°F. Thus off-design performance is predicted for the evaporator. With an economizer or superheater, More calculations are involved as the water or steam temperature changes. Also, the duty is affected by the configuration of the exchanger, whether counterflow, parallel flow, or crossflow. The NTU method discussed in Q8.29 and Q8.30 may be used to predict the off-design performance of such an exchanger.
Discuss the logic for determining the off-design performance of a water tube waste heat boiler with the configuration shown in Fig. 8.4.
In the design procedure one calculates the size of the various heating surfaces such as superheaters, evaporators, and economizers by the methods discussed earlier based on the equation A = Q/(U x AT). In this situation, the duty Q, log — mean temperature difference AT, and overall heat transfer coefficient U are known or can be obtained easily for a given configuration.
In the off-design procedure, which is more involved, the purpose is to predict the performance of a given boiler under different conditions of gas flow, inlet gas temperature, and steam parameters. In these calculations several trial — and-error steps are required before arriving at the final heat balance and duty, because the surface area is now known. The procedure is discussed for a simple case, configuration 1 of Fig. 8.4, which consists of a screen section, superheater, evaporator, and economizer.
1. Assume a steam flow Ws based on gas conditions.
2. Solve for the screen section, which is actually an evaporator, by using the methods discussed in Q8.15a.
|
FIgure 8.4 Configurations for water tube boiler. |
Solve for the superheater section, either using the NTU method or by trial and error. Assume a value for the duty and compute the exit gas/steam temperatures and then AT.
Assumed duty Qa = WgCp(Tg, — Tgo)hlf
= Ws(hso — hsi)
Where
Hso, hsi = enthalpies of steam at exit and inlet Tgi, Tgo = gas inlet and exit temperatures.
Compute U. Then transferred duty is Qt = U x A x AT. If Qa and Qt are close, then the assumed duty and gas/steam temperatures are correct; proceed to the next step. Otherwise assume another duty and repeat step 3.
4. Solve for the evaporator section as in step 1. No trial and error is required, because the steam temperature is constant.
5. Solve for the economizer as in step 3. Assume a value for the duty and then compute exit gas/water temperatures, AT, and Qt. Iteration proceeds until Qa and Qt match. The NTU method can also be used to avoid several iterations.
6. The entire HRSG duty is now obtained by adding the transferred duty of the four sections. The steam flow is corrected based on the actual total duty and enthalpy rise.
7. If the actual steam flow from step 6 equals that assumed in step 1, then the iterations are complete and the solution is over; if not, go back to step 1 with the revised steam flow.
The calculations become more complex if supplementary firing is added to generate a desired quantity of steam; the gas flow and analysis change as the firing temperature changes, and the calculations for U and the gas/steam temperature profile must take this into consideration. Again, if multipressure HRSGs are involved, the calculations are even more complex and cannot be done without a computer.
Determine the tube metal temperature for the case of a superheater under the following conditions:
Average gas temperature = 1200°F
Average steam temperature = 620°F
Outside gas heat transfer coefficient = 15 Btu/ft2h°F
Steam-side coefficient = 900 Btu/ft2 h °F
(Estimation of steam and gas heat transfer coefficients is discussed in Q8.03 and Q8.04.)
Tube size = 2 x 0.142 in. (2in. OD and 0.142 in. thick)
Tube thermal conductivity = 21 Btu/fth °F (carbon steel)
(Thermal conductivity of metals can be looked up in Table 8.9.)
Because the average conditions are given and the average tube metal temperature is desired, we must have the parameters noted above under the most severe conditions of operation—the highest gas temperature, steam temperature, heat flux, and so on.
Material 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500
|
Aluminum (annealed)
|
(continued )
|
Temperature (°F)
|
Let us use the concept of electrical analogy, in which the thermal and electrical resistances, heat flux and current, and temperature difference and voltage are analogous. For the thermal resistance of the tube metal,
D d 2 ,2
= _ .,, ln — = ——— x ln ■
M 24Km ‘ d 24 x 21" ‘1.72
= 0.0006 ft2 h °F/Btu
Outside gas film resistance
Ro = = 0.067 ft2 h °F/Btu
12
Inside film resistance R, =—— = 0.0011 ft hr °F/Btu
‘ 900 ‘
Total resistance Rt 0.067 0.0006 0.0011
= 0.0687 ft2 h °F/Btu
Hence
1200 — 620 2 Heat flux Q = —0 0687— = 8443 Btu/ft h
Temperature drop across the gas film = 8443 x 0.067 = 565°F
Temperature drop across the tube metal = 8443 x 0.0006 = 5°F
Temperature drop across steam film = 8443 x 0.0011 = 9.3°F
(Here we have applied the electrical analogy, where voltage drop is equal to the product of current and resistance.) Hence,
* . (1200 — 565) + (620 + 9.3)
Average tube metal temperature =—————— 2—————— = 632 F
We note that the tube metal temperature is close to the tube-side fluid temperature. This is because the tube-side coefficient is high compared to the gas heat
Transfer coefficient. This trend would prevail in equipment such as water tube
Boilers, superheaters, economizers, or any gas-liquid heat transfer equipment.
An approximation of the tube metal temperature for bare tubes in a gasliquid or gas-gas heat transfer device is
Hi
Tm = to — , (to — ti) (35)
Hi + ho
Where
Ht, ho =heat transfer coefficients inside and outside the tubes, Btu/ft2h°F t,, to = fluid temperatures inside and outside, °F
In a boiler air heater, ho = 9, ht = 12, tt = 200°F, and to = 800°F. Estimate the average tube wall temperature tm.
Using Eq. (35), we have 12
Tm = 800 ————- x (800 — 200) = 457°F
M 12 + 9
How is the performance of fire tube and water tube boilers evaluated? Can we infer the extent of fouling from operational data? A water tube waste heat boiler as shown in Fig. 8.5 Generates 10,000 lb/h of saturated steam at 300psia when the gas flow is 75,000 lb/h and gas temperatures in and out are 1000°F and 500°F. What should the steam generation and exit gas temperature be when 50,000 lb/h of gas at 950°F enters the boiler?
It can be shown as discussed in Q8.15a that in equipment with a phase change [1,8],
Ln t1 — tsat __ UA
T2 — tsat WgCp
Which was given there as Eq. (34).
For fire tube boilers, the overall heat transfer coefficient is dependent on the gas coefficient inside the tubes; that is, U is proportional to Wg, • 8. In a water tube boiler, U is proportional to Wg,• 6. Substituting these into Eq. (34) gives us the following.
|
FIgure 8.5 Sketch of (a) fire tube and (b) water tube boilers. |
For fire tube boilers:
|
H ~ ^si t9 tst |
|
Ln |
 |
|
|
|
||
For water tube boilers:
|
T1 ~ ^sa To |
|
Ln |
|
|
 |
|
|
|
As long as the fouling is not severe, Eqs. (36) and (37) predict the exit gas temperatures correctly. If t2 is greater than predicted, we can infer that fouling has occurred. Also, if the gas pressure drop across the boiler is more than the calculated value (see Chap. 7 for pressure drop calculations), we can infer that fouling has taken place.
Calculate K2 from Eq. (37). tsat = 417 from the steam tables (see the Appendix).
K2 = In f1000—417) x (75,000)° 4 = 173
2 500 — 417 7 ’
Let us predict the exit gas temperature when Wg = 50,000.
Ln (95° ~417) =^50’000^0 4 = 2.29 V t2 — 417 / 173
950 -417 t2 = 417 + ^29) = 471°F
Now the actual exit gas temperature is 520°F, which means that the fouling is severe.
The energy loss due to fouling is Q = 50,000 x 0.26 x (520 — 471)
= 0 . 63 x 106 Btu/h
If energy costs $3/MMBtu, the annual loss of energy due to fouling will be
3 x 0.63 x 8000 = $15,120 (assuming 8000 hours of operation a year).
When and where are finned tubes used? What are their advantages over bare tubes?
Finned tubes are used extensively in boilers, superheaters, economizers, and heaters for recovering energy from clean gas streams such as gas turbine exhaust or flue gas from combustion of premium fossil fuels. If the particulate concentration in the gas stream is very low, finned tubes with a low fin density may be used. However, the choice of fin configuration, particularly in clean gas applications, is determined by several factors such as tube-side heat transfer coefficient, overall size, cost, and gas pressure drop, which affects the operating cost.
Solid and serrated fins (Fig. 8.6) are used in boilers and heaters. Finned surfaces are attractive when the ratio between the heat transfer coefficients on the outside of the tubes to that inside is very small. In boiler evaporators or economizers, the tube-side coefficient could be in the range of 1500- 3000Btu/ft2h °F, and the gas-side coefficient could be in the range of 10-
|
Figure 8.6 Solid and serrated fins. |
20Btu/ft2h °F. A large fin density or a large ratio of external to internal surface area is justified in this case. As the ratio between the outside and inside coefficients decreases, the effectiveness of using a large ratio of external to internal surface areas decreases. For example, in superheaters or high pressure air heaters, where the tube-side coefficient could be in the range of 30- 300Btu/ft2h °F, it does not pay to use a large fin surface; in fact, it is counterproductive, as will be shown later. A moderate fin density such as two or three fins per inch would be adequate, whereas for economizers or evaporators, five or even six fins per inch may be justified if cleanliness permits.
The other important fact to be kept in mind is that more surface area does not necessarily mean more energy transfer. It is possible, through poor choice of fin configuration, to have more surface area and yet transfer less energy. One has to look at the product of surface area and overall heat transfer coefficient and not at surface area alone. The overall heat transfer coefficient is significantly reduced as we increase the fin surface or use more fins per inch.
Finned tubes offer several advantages over bare tubes such as a compact design that occupies less space, lower gas pressure drop, lower tube-side pressure drop due to the fewer rows of tubes, and smaller overall weight and cost.
Solid fins offer slightly lower gas pressure drop than serrated fins, which have a higher heat transfer coefficient for the same fin density and configuration. Particulates, if present, are likely to accumulate on serrated finned tubes, which may be difficult to clean.
How are the heat transfer and pressure drop over finned tubes and tube and fin wall temperatures evaluated?
The widely used ESCOA correlations developed by ESCOA Corporation [9] will be used to evaluate the heat transfer and pressure drop over solid and serrated finned tubes in in-line and staggered arrangements. The basic equation for heat transfer coefficient with finned tubes is given by Eq. (3).
The calculation for tube-side coefficient ht was discussed earlier. ho consists of two parts, a nonluminous coefficient hN, which is computed as discussed in Q8.07, and hc, the convective heat transfer coefficient. Computation of hc involves an elaborate procedure and the solving of several equations, as detailed below.
Determination of Hc [9]
D + 2 h• 5 fte + 460 • 25
TOC o "1-5" h z hc = C3 Ci C51 —-— x
D ) ta + 460
|
( |
!0 • 67
A) (38)
Wg
G = [(Sr/12) -Ao]NwL (39)
D nbh _ N
Ao = 12 + -6T (40)
C1; C2, and C3 are obtained from Table 8.10.
Gd
Re = 12m (41)
S =—— b (42)
n
Fin Efficiency and Effectiveness
For both solid and serrated fins, effectiveness z is
Af
Z = 1 -(1 — E) A (43)
C = 0 . 25 Re-035 C2 = 0 . 07 + 8Re-045 In-line
C3 = 0 . 2 + 0 . 65e-025h/s C4 = 0 . 08(0 .15ST/d)-11^ 15 C5 = 1.1 — (0 . 75 — 1. 5e-0. 7Nd)e-2 . 0SL/ST C6 = 1. 6 — (0 . 75 — 1. 5e-0. 7Nd)e-0 . 2(Sl/st)2 Staggered o 2o
C3 = 0.35 + 0.65e-0 . 25h/s C4 = 0 .11 (0 .15ST/d)-0 : 7(h/s)0 20 C5 = 0 . 7 + (0 . 7 — 0 . 8e-0 15Nd2)e-1 0SL/ST
C6 = 1.1 +(1. 8 — 2 .1 e-0 15Nd2)e-2 . 0(sl/st) — (0 . 7 — 0 . 8e-0 15Nd2)e-0 6(SL/Sr)
C1 = 0 . 25 Re-035 C2 = 0 . 07 + 8 . 0Re-0 45 In-line
C3 = 0 . 35 + 0 . 5e-035h/s C4 = 0 . 08(0 .15ST/d)-11(h/s)0 2 C5 = 1.1 — (0 . 75 — 1. 5e-0. 7Nd)e-2. 0SL/ST C6 = 1. 6 — (0 . 75 — 1. 5e-0 7wd)e-0.2(st/sr)2 Staggered
C3 = 0.55 + 0.45e-0 . 35h/s C4 = 0 .11 (0 . 05ST/d)-0 . 7(h/s)0 23 C5 = 0 . 7 + (0 . 7 — 0 . 8e-0 15Nd2)e-1 0SL/ST
C6 = 1.1 +(1. 8 — 2 .1 e-0 15Nd2)e-2. 0(sl/st) — (0 . 7 — 0 . 8e-0 15Nd2)e-0. 6(sl/st)
Source: Fintube Technologies, Tulsa, OK.
For solid fins,
|
Af = pn x—————— ————————————————————— (44) At = Af + p (45) |
4dh + 4h2 + 2bd + 4bh
^4"
D(1 — nb)
T2"
TOC o "1-5" h z E = 1/{1 + 0.002292 m2h2 [(d + 2h)/d]0 5} (46)
Where
M = (24ho /Kb)0 • 5 (47)
For serrated fins,
|
Af = pdn ———— ————— (48) |
2h(ws + b) + bws 12 ws
At = Af + pd (1 12nb) (49)
E =tanh (mh) (50)
mh
C = 0 •053(1.45 — 2.9Sl/d)-2 • 3 Re-0 • 21 C2 = 0 .11 + 1.4 Re-0• 4
C3 = 0 •20 + 0. 65e-025h/s C4 = 0 . 08(0 .15ST/d)-11(h/s>0 15
C5 = 1.1 — (0 . 75 — 1. 5e-0• 7Nd)e-2• 0Sl/st c6 = 1. 6 — (0 . 75 — 1.5e-0 • 7Nd)e-0 • 2(Sl/st)2
J = C C3C5[(d + 2h)/d]0 5[(tg + 460)/(ta + 460)]° 5 f = C2C4C6[(d + 2h)/d][(tg + 460)/(ta + 460)]0 • 25 Staggered
C1 = 0 . 091 Re-0 • 25 C2 = 0.075 + 1.85 Re-0 • 3 o 2o
C3 = 0.35 + 0. 65e-025h/s C4 = 0 .11 (0 . 05ST/d)[4]
|
-°-6(Sl/St ) |
C5 = 0 . 7 + (0 . 7 — 0 . 8e-0 15Nd2)[e-10SL/ST] C6 = 1.1 +(1. 8 — 2 .1 e-0 15Nd2)e-2 0(SL/ST> — [0 . 7 — 0 .8e-0 •15N2]e~
J = C1 C3C5[(d + 2h/d]05[(fg + 460)/(ta + 460)]05
F = C2C4C6[(d + 2h)/d]0 • 5[( tg + 460)/( ta + 460)]-0 • 25
C1 = 0.053(1.45 — 2.9Sl/d)-2 • 3 Re-0 • 21 C2 = 0 .11 + 14 Re-0 • 4
C3 = 0 . 25 + 0 . 6e-026h/s C4 = 0 . 08(0 .15ST/d)^•H^)015
C5 = 1.1 — (0 . 75 — 1. 5e-0• 7Nd)e-2 • 0SL/ST C6 = 1. 6 — (0 . 75 — 1.5e-0 • 7Nd)e-0 • 2(Sl/st)2
J = C1 C3C5[(d + 2h)/d]0 5[( tg + 460)/( ta + 460)]0 5 f = C2C4C6[(d + 2h)/d][(tg + 460)/(ta + 460)]0 • 25 Staggered
C1 = 0 . 091 Re-0 • 25 C2 = 0.075 + 1.85 Re-0 • 3 o
C3 = 0 •35 + 0. 65e-0 17h/s C4 = 0 .11 (0 . 05ST/d)2
|
°:6(Sl/St ) |
C5 = 0 • 7 + (0 . 7 — 0 . 8e-0 15Nd2)e-10SL/st C6 = 1.1 +(1. 8 — 2 .1 e-0 15Nd2)e-2 0(SL/ST) — (0 .7 — 0 .8e-0 15Nd2)e-
J = C CsCsKd + 2h)/d]° :5[(fg + 460)/(fa + 460)]° 25 f = C2C4C6[(d + 2h)/d]° ■ 5[(fg + 460)/(fa + 460)]-° ■ 25
Where
Kbws
Gas pressure drop APg is
DPg = (f + a) Pg x 1.083d X 109 (52)
Where
2h 0 5
TOC o "1-5" h z f = C2C4C6 x ^—-—J for staggered arrangement (53)
D ~)- 2h
= C2C4C6 x—— — for in-line arrangement (54)
D
1 + B2 tg2 — tgi
A 4Nd X 4(50 + tg (55)
B = ffree gaS areaV (56)
total area /
C2, C4, C6 are given in Table 8.10 for solid and serrated fins.
Tube Wall and Fin Tip Temperatures
For solid fins the relationship between tube wall and fin tip temperatures is given
By
TOC o "1-5" h z tg — tf = K1(mre) x I0(mre) + I1(mre) X K0(mre) (57)
Tg — tb Ki(mre) x Io(mro) + Ko(mr0) x ^1 (mre)
The various Bessel functional data are shown in Table 8.11 for serrated fins, treated as longitudinal fins:
Tg — tf 1
Tg—f = (58)
Tg — tb cosh(mb)
A good estimate of tf can also be obtained for either type of fin as follows:
Tf = tb + (tg — tb) x (1. 42 — 1. 4 E) (59)
Tb, the fin base temperature, is estimated as follows:
Tb = ti + q (R3 + R4 + R5) (60)
Where R3, R4, and R5 are resistances to heat transfer of the inside film, fouling
Layer, and tube wall, respectively, and heat flux qo is given by
Q0 = Uo(tg-1,) (1)
The following example illustrates the use of the equations.
|
X |
Wx) |
/1(x) |
K)(x ) |
K1(x) |
|
0 |
1.0 |
0 |
8 |
8 |
|
0.1 |
1.002 |
0.05 |
2.427 |
9.854 |
|
0.2 |
1.010 |
0.10 |
1.753 |
4.776 |
|
0.3 |
1.023 |
0.152 |
1.372 |
3.056 |
|
0.4 |
1.040 |
0.204 |
1.114 |
2.184 |
|
0.5 |
1.063 |
0.258 |
0.924 |
1.656 |
|
0.6 |
1.092 |
0.314 |
0.778 |
1.303 |
|
0.7 |
1.126 |
0.372 |
0.66 |
1.05 |
|
0.8 |
1.166 |
0.433 |
0.565 |
0.862 |
|
0.9 |
1.213 |
0.497 |
0.487 |
0.716 |
|
1.0 |
1.266 |
0.565 |
0.421 |
0.602 |
|
1.2 |
1.394 |
0.715 |
0.318 |
0.434 |
|
1.4 |
1.553 |
0.886 |
0.244 |
0.321 |
|
1.6 |
1.75 |
1.085 |
0.188 |
0.241 |
|
1.8 |
1.99 |
1.317 |
0.146 |
0.183 |
|
2.0 |
2.28 |
1.591 |
0.114 |
0.140 |
|
2.2 |
2.629 |
1.914 |
0.0893 |
0.108 |
|
2.4 |
3.049 |
2.298 |
0.0702 |
0.0837 |
|
2.6 |
3.553 |
2.755 |
0.554 |
0.0653 |
|
2.8 |
4.157 |
3.301 |
0.0438 |
0.0511 |
|
3.0 |
4.881 |
3.953 |
0.0347 |
0.0402 |
|
3.2 |
5.747 |
4.734 |
0.0276 |
0.0316 |
|
3.4 |
6.785 |
5.670 |
0.0220 |
0.0250 |
|
3.6 |
8.028 |
6.793 |
0.0175 |
0.0198 |
|
3.8 |
9.517 |
8.140 |
0.0140 |
0.0157 |
|
4.0 |
11.30 |
9.759 |
0.0112 |
0.0125 |
|
4.2 |
13.44 |
11.70 |
0.0089 |
0.0099 |
|
4.4 |
16.01 |
14.04 |
0.0071 |
0.0079 |
|
4.6 |
19.09 |
16.86 |
0.0057 |
0.0063 |
|
4.8 |
22.79 |
20.25 |
0.0046 |
0.0050 |
|
5.0 |
27.24 |
24.34 |
0.0037 |
0.0040 |
A steam superheater is designed for the following conditions.
Gas flow = 225,000 pph Gas inlet temperature = 1050°F Gas exit temperature = 904°F
Gas analysis (vol%): CO2 = 3, H2O = 7, N2 = 75, O2 = 15
Steam flow = 50,000 pph Steam temperature in = 501°F (sat)
Steam exit temperature = 758°F Steam pressure (exit) = 650 psig
Tubes used: 2 x 0.120 low alloy steel tubes; 18 tubes/row, 6 deep, 10 ft long, in-line arrangement with 4 in. square pitch and nine streams. Tube inner diameter = 1.738 in.; outer diameter = 2 in.
Fins used: solid stainless steel, 2 fins/in., 0.5 in. high and 0.075 in. thick. Fin thermal conductivity K = 15 Btu/fth °F.
Determine the heat transfer coefficient and pressure drop.
So/wt/on.
A = H + 2 x 0 • 56x 0 •075 = 0.17917 ft2/ft
G =__________ ^____________ — = 8127 lb/ft2 h
18 x 10 x [(4/12) — 0.17917)] ‘
The gas properties at the average gas temperature (from the Appendix) are
Cp = 0.276, m = 0.086, k = 0 .03172
8127 x 2
Re =—————- = 15,750
12 x 0 .086
C = 0 .25 x (15,750)-0.35 = 0 .0085
S = 1/2 — 0.075 = 0.425
C3 = 0 .2 + 0 .65 e-0 425 = 0.6843
C5 = 1.1 — (0 .75 — 1. 5 e-0 7×6) (e-2×4/4) = 1. 0015
Assume that the average fin temperature is 750°F. The average gas temperature = 977°F, and steam temperature = 630°F. The fin thermal conductivity K is assumed to be 15 Btu/fth °F. Then,
/3^ 0
Hc = 0.0085 x 0.6843 x 1.0015 x (- 977 + 460° . 25
75^) x 8127 x 0.276
0.
|
20 29 |
03172 x° 67
0. 276 x 0.086
Using methods discussed in Q8.07, we find hN = 1.0. The beam length for finned tubes is computed as 3.4 x volume/surface area. Hence
H0 = 20.29 + 1.0 = 21.29
24 x 21.29°-5=21 31
V15 x 0.075y
E = 1/(1 +0.002292 x 21.31 x 21. 31 x 0.5 x 0.5 x VL5)
= 0 . 758 Af = 3.14 x 2
4 x 2 x 0.5 + 4 x 0.5 x 0. 5 + 2 x 0.075 x 2 + 4 x 0.075 x 5
X————————————————————————————-
24
= 1. 426
At = 1.426 + 3 .14 x 2 x 1 — 2 x 0.075 = L 871 ‘ 12
Hence
Z = 1 — (1 — 0.758) 1426 = 0 .8156 1 871
Let us compute h, for steam. w = 50,000/9 = 5555 lb/h per tube. From Table 8.2, factor C = 0.34.
X0 . 8
(5555)0 2
H = 2.44 x 0.34 x ———— ^ = 303 Btu/ft[5] h °F
‘ (1.738)1’ 8
1 1 1 871
■+ 12 x ■
U 21.29 x 0.816 303 x 3.14 x 1.738
+ 0.001 + 0.001 x 1 871 x 12 + 24 ln ^ 2
3.14 x 1. 738 1. 738
1 871
24 x 20 x 3 14 x 1 738 = 0.0576 + 0.01358 + 0.001 + 0.0041 + 0.0032
= 0.0795 or U = 12 .58 Btu/ft2hF
Calculation of Tube Wall and Fin Tip Temperature
Heat flux q = 12.58 x (977 — 630) = 4365 Btu/ft2 h tb = 630 + 4365 x (0.0032 + 0.0041 + 0.01358) 722°F
1. 5
Mre = 21.29 x — = 2.661 ft, mro = 1.7742 ft
E 12
K0 (2. 661) = 0.0517 K1 (2.661) = 0.061
I0(2. 661) = 3. 737, I1(2.661) = 2. 921
K0(1.7742) = 0.1515, I0(1. 7742) = 1. 959
Hence,
977 — tf 0.061 x 3 .737 + 2.921 x 0.0517
———- }— =——————————————— = 0.6743
977 — 722 0.061 x 1.959 + 0.1515 x 2. 921
Tf = 805 °F Using the approximation
Tf = tb + (1.42 — 1.4 x 0.758) x (977 — 722) = 813°F
Note that this is only an average base and fin tip temperature. For material selection purposes one should look at the maximum heat flux, which occurs, for instance, at the gas inlet in a counterflow arrangement, and also consider the nonuniformity or maldistribution in gas and steam flow. A computer program can be developed to compute the tube wall and fin tip temperatures at various points along the tube length and the results used to select appropriate materials.
It can be noted from the above that there are a few ways to reduce the fin tip temperature:
C2 = 0 .07 + 8 x (15,750)~° 45 = 0 .1734
|
C4 = 0 . 08 x (0 .15 x 2) |
1.11 x(0 .5/0 .425)°’15 _ 0 3107
|
DPg = (0.0808 — 0.0051) x 8120 x 8120 x |
|
6 0.0271 x 1.083 x 109 |
|
904 — 1050 1 +0.2134 460 + 977 x 24 |
|
= -0 . 005 |
|
|
|
|
|
|
 |
|
 |
= 1. 02 in. WC
(Gas density = 0.0271. )
Computer solution of the above system of equations saves a lot of time. However, I have developed a chart (Fig. 8.7) that can be used to obtain hc (or hg) and z values for serrated fins and an in-line arrangement for various fin configurations and gas mass velocities for gas turbine exhaust gases at an average gas temperature of 700°F. Although a computer program is the best tool, the chart can be used to show trends and the effect of fin configuration on the performance of finned surfaces. The use of the chart is explained later with an example. The following points should be noted.
1. From Fig. 8.7, it can be seen that for a given mass velocity, the higher the fin density or height, the lower the gas-side coefficient or effectiveness, which results in lower Uo. The amount of energy transferred in heat transfer equipment depends on the product of the overall heat transfer coefficient and surface area and not on the surface area alone. We will see later that one can have more surface area and yet transfer less duty due to poor choice of fin configuration.
2. Higher fin density or height results in higher APg. Even after adjusting for the increased surface area per row, it can be shown that the higher the fin density or the greater the height, the higher the gas pressure drop will be for a given mass velocity.
|
Figure 8.7 Chart of convective heat transfer coefficient and pressure drop versus fin geometry. (Data from Ref. 10) |
Describe Briggs and Young’s correlation.
Charts and equations provided by the manufacturer of finned tubes can be used to obtain hc. In the absence of such data, the following equation of Briggs and Young for circular or helical finned tubes in staggered arrangement [4] can be used.
12k =0 ^ (62)
Simplifying, we have
/G0 . 681 Zk0 ■ 67 c0 ■ 33 / S0 .313
Hc = 0 ■295 (d0319′) ( mi. o ■ 35i ) (63)
Where
G
NWL(ST/12 -A0)
S = fin clearance = 1 /n — b, in [Eq. (42)]
D, h, b = tube outer diameter, height, and thickness, in.
D nbd 2
A0 = fin obstruction area = — H——, ft /ft [Eq. (40)]
12 6
The gas properties Cp, m, and k are evaluated at the average gas temperature.
The gas heat transfer coefficient hc has to be corrected for the temperature
Distribution along the fin height by the fin efficiency
E =—————- * , (64)
1 / mh Id + 2h
+ 3W2
Where
L24h
M= /*i [Eq.(47)]
Km is the fin metal thermal conductivity, in Btu/fth°F.
In order to correct for the effect of finned area, a term called fin effectiveness is used. This term, z, is given by
Af
Z = 1 -(1 — E)x-f — [Eq. 43]
At
Where the finned area Af and total area At are given by
Pn
Af = — (4dh + 4h2 + 2bd + 4bh) [Eq . (44)]
Pd
At = Af + — (1 — nb) [Eq. (45)]
N is the fin density in fins/in. The factor
K0 . 67 c0 . 33
F(65) is given in Table 8.12.
The overall heat transfer coefficient with finned tubes, U, can be estimated as U = 0 . 85zhc, neglecting the effect of the non-luminous heat transfer coefficient.
TAble 8.12 Factor F for Finned Tubes
|
F |
Temp (°F)
|
|
Determine the gas-side heat transfer coefficient when 150,000 lb/h of flue gases at an average temperature of 900°F flow over helically finned economizer tubes with the following parameters:
D = tube outer diameter = 2.0 in. n = fins/in. = 3 h = fin height = 1 in. b = fin thickness = 0.06 in.
L = effective length of tubes = 10.5 ft Nw = number of tubes wide = 12
= transverse pitch = 4.5 in. (staggered)
Calculate Ao, Af, and At. From Eq. (40),
A0 = — + 3 x 0 . 06 x 1 = 0 . 2 ft2/ft
0
12 6
From Eq. (44),
|
+ 2 x 0.06 x 2 + 4 x 0.06) = 4. 9 ft2/ft |
From Eq. (45),
|
|
|
At = 4 . 9 + p |
G =_________ ^__________ — = 6800 lbf h
12 x 10 . 5 x (4 . 5/12 -0 . 2) ‘
Fin pitch S = 1 — 0 . 06 = 0 . 27
Using Eq. (65) with F = 0.145 from Table 8.12 Gives us h= 0.295 x 68800• 681 x 0 .145
0.27a313
= 12 . 74 Btu/ft2 h °F
20319 x 10 -2 x 0 . 060 113
Calculate fin efficiency from Eq. (64). Let metal thermal conductivity of fins (carbon steel) = 24Btu/fth °F.
M = J————- = 14 . 57
24 x 0 06
E =————————————— 2—- . = 0 . 6
1 + 0.33 x (14.57 x 1/12)2 x V(2 + 2)/2
4 9
Fin effectiveness z = 1 — (1 — 0 • 6) 5-— = 0 • 63 Hence,
Zhc = 0.63 x 12.74 = 8 Btu/ft2 h °F
Ranges from 23 to 27 Btu/ft h °F for carbon steels, depending on temperature [1]. For alloy steels it is lower.
8.19c
Q:
This example shows how one can predict the performance of a given heat transfer surface. A superheater is designed for the following conditions: 18 tubes/row, 6 rows deep, 10 ft long with 2 fins/in., 0.5 in. high and 0.075 in. thick solid fins. It has 18 streams. Surface area = 2022 ft2. Tube spacing = 4 in. square.
Predict the performance of the superheater under the following conditions:
Gas flow = 150,000 lb/h at 1030°F
Steam flow = 35,000 lb/h at 615psig sat
Flue gas analysis (vol%): CO2 = 7, H2O = 12, N2 = 75, O2 = 6
Heat loss = 2%
Surface area A 2022 ft2
Let us say that U has been estimated as 10.6 Btu/ft2 h °F using methods discussed earlier.
Let us use the NTU method to predict the performance of the superheater. This is discussed in Q8.30. The superheater is in counterflow arrangement.
Energy transferred Q = eCmin(tg — tSi )
Where
1 — exp[—NTU(1 — C)]
E = ■
1 — C exp[-NTU(1 — C)]
C Cmin/Cmax
Cmin is the lower of (mass x specific heat of the fluid) on gas and steam sides.
Tgi, t = gas and steam temperature at inlet to superheater, °F
Use 491 °F for steam saturation temperature.
Though NTU methods generally require no iterations, a few rounds are necessary in this case to evaluate the specific heat for steam and gas, which are functions of temperature. However, let us assume that the steam-side specific heat = 0.6679 and that of gas = 0.286 Btu/lb °F.
Cgas = 150,000 x 0.98 x 0.286 = 42,042 Csteam = 35,000 x 0. 6679 = 23,376
Hence, Cmin = 23,376.
C = = 0 . 556
42,042
10.62 x 2022 NTU = UA/Cmin = 23 376 = 0.9186
Hence
1 — exp[—0.9186 x (1 — 0.556)] = 0 5873
1 — 0.556 exp[—0.9186 x (1 — 0. 556)] .
Hence
Energy transferedQ = 0.5873 x 23,376 x (1030 — 491) = 6.7 MMBtu/h
6,700,000
Exit steam temperature =————————— h 491 = 287 + 491 = 778 F
F 35,000 x 0.06679
6,700,000
T gas = 1030 — 150.000 x 0. 286 x 0 .98 = 871 °F
Steam-side pressure drop is obtained as follows:
Equivalent length of tube = (18/9) x 6 x 10 + (18/9) x 6 x 2 .5 x 2 = 180 ft
/352 185
Pressure drop = 3. 36 x 0.02 x 0.956 x I — j ^ pyggs = H4 psi
Gas-side pressure drop may be estimated using the chart in Fig. 8.7 And is about
0.6in. WC.
8.20 Q:
A gas turbine HRSG evaporator operates under the following conditions:
Gas flow = 230,000 lb h (vol % CO2 = 3, H2O = 7, N2 = 75, O2 = 15)
Gas inlet temperature = 1050°F Exit gas temperature = 406°F
Duty = 230,000 x 0.99 x 0.27 x (1050 — 406) = 39.6 MM Btu/h Steam pressure = 200 psig Feedwater temperature = 230°F Blowdown = 5%
Fouling factors = 0.001 ft2h °F/Btu on both gas and steam sides
Arrangement: 4 in. square pitch
Tubes used: 2 x 1.773 in., 24 tubes/row, 11 ft long
Fins: 5 fins/in., 0.75 in. high, 0.05 in. thick, serrated
Determine the overall heat transfer coefficient and pressure drop using the chart.
The chart shown in Fig. 8.7 has been developed for serrated fins in in-line arrangement for the above gas analysis. Users may develop their charts for
Various configurations or use a computer program. The chart is based on an average gas temperature of 700°F and a gas analysis (vol%) of CO2 = 3, H2O = 7, N2 = 75, O2 = 15.
Ao = 12 + ^5 x 0 . 75 x 005) = 0.1979 ft2/ft
230,0 2
G = 24 x 11 x (0.3333 -0.1979) = 6434lb/ft2 h
Average gas temperature = 728°F. From Table 8.12, the correction factor is
0. 1402/0.139 = 1.008.
For G = 6434, hc from the chart = 11.6 Btu/ft2 h °F, Gas pressure drop over
10 rows = 1.7 in. WC.
Fin effectiveness = 0.75
HN is small, about 0.4 Btu/ft2 h °F
H0 = 0.75 x (0.4 + 1.008 x 11.6) = 9.07Btu/ft2h°F
The fin total surface area can be shown to be 5.7 ft2/ft.
Hence
At 5 7 x 12
— =——————- = 12 29
At 3 .14 x 1. 773 ‘
Let tube-side boiling coefficient = 2000 Btu/ft2 h °F and fin thermal conductivity = 25 Btu/fth °F
I = _L + 0.001 x 12 .29 + 0.001 +1229 + 12 ,29 x 2 xln(2/L773)
U 9.07 2000 24/25
= 0.110 + 0.01229 + 0.001 + 0.006145 + 0.004935 = 0.1344 U = 7 . 4 Btu/ft2 h °F
T. . ,.ff (1050 — 388)-(406 — 388)
Log-mean temperature difference =
Ln[(1050 — 388)/(406 — 388)] = 178°F
TOC o "1-5" h z 39 6 x 106 2
Surface area required = —:————— = 30,063 ft
H 178 x 7 . 4
30 063
Number of rows deep required = ——— 7——— = 20
F H 24 x 11 x 5 . 7
Gas pressure drop = 1. 7 x 2 = 3. 4 in. Wc
How does a finned surface compare with a bare tube bundle for the same duty? A:
Let us try to design a bare tube boiler for the same duty as above. Use the same tube size and spacing, tubes per row, and length. Use 2 x 1.773 in. bare tubes.
Using the procedure described in Q8.14, we can show that U = 13.05 Btu/ft2h °F and that 124 rows are required for the same duty. The results are shown in Table 8.13.
It may be seen that the finned tube bundle is much more compact and has fewer rows and also a lower gas pressure drop. It also weighs less and should cost less. Therefore, in clean gas applications such as gas turbine exhaust or fume incineration plants, extended surfaces may be used for evaporators. In dirty gas applications such as municipal waste incineration or with flue gases containing ash or solid particles, bare tubes are preferred. Finned tubes may also be used in packaged boiler evaporators.
However, the heat flux inside the finned tubes is much larger, which is a concern in high gas temperature situations. The tube wall temperature is also higher. Hence when the gas temperature is high, say 1400-1700° F, we use a few
|
Table 8.13 Comparison of Bare Tube and Finned Tube Boilers
|
|
Tubes/row = 24; effective length = 11 ft; 4 in. square spacing. Gas analysis (vol%) CO2 = 3 H2 = 7, N2 = 75, O2 = 15. Blowdown = 5%. |
Bare tubes followed by tubes with, say, 2 fins/in. fin density and then go back to four or more fins per inch. This ensures that the gas stream is cooled before entering tube bundles with a high fin density and that the tubes are operating at reasonable temperatures, which should also lower the fin tip temperatures.
8.22 Q:
Which is the preferred arrangement for finned tubes, in-line or staggered?
Both in-line and staggered arrangements have been used with extended surfaces. The advantages of the staggered arrangement are higher overall heat transfer coefficients and smaller surface area. Cost could be marginally lower depending on the configuration. Gas pressure drop could be higher or lower depending on the gas mass velocity used. If cleaning lanes are required for soot blowing, an inline arrangement is preferred.
Both solid and serrated fins are used in the industry. Generally, solid fins are used in applications where the deposition of solids is likely.
The following example illustrates the effect of arrangement on boiler performance.
150,0 lb/h of turbine exhaust gases at 1000°F enter an evaporator of a waste heat boiler generating steam at 235psig. Determine the performance using solid and serrated fins and in-line versus staggered arrangements. Tube size is
2 x 1.77 in.
Solution. Using the ESCOA correlations and the methodology discussed above for evaporator performance, the results shown in Table 8.14 Were arrived at.
How does the tube-side heat transfer coefficient or fouling factor affect the selection of fin configuration such as fin density, height, and thickness?
TAble 8.14 Comparison Between Staggered and In-Line Designs for Nearly Same Duty and Pressure Dropa
|
Serrated fins |
Solid fins |
|
In-line Staggered |
In-line Staggered |
|
Fin config. |
5 x 0.75 |
X 0.05×0.157 |
2 x 0.75 |
X 0.05 x 0 |
|
Tubes/row |
18 |
20 |
18 |
20 |
|
No. of fins deep |
20 |
16 |
20 |
16 |
|
Length |
10 |
10 |
10 |
11 |
|
U0 |
7.18 |
8.36 |
9.75 |
10.02 |
|
APg |
3.19 |
3.62 |
1.72 |
1.42 |
|
Q |
23.24 |
23.31 |
21.68 |
21.71 |
|
Surface |
20,524 |
18,244 |
9802 |
9584 |
|
A Duty, MM Btu/h; APg, in. WC; surface, ft2; temperature, °F; Uo, Btu/ft2 h °F. |
Fin density, height, and thickness affect the overall heat transfer coefficient as can be seen in Fig. 8.7. However, the tube-side coefficient also has an important bearing on the selection of fin configuration.
A simple calculation can be done to show the effect of the tube-side coefficient on Uo. It was mentioned earlier that the higher the tube-side coefficient, the higher the ratio of external to internal surface area can be. In other words, it makes no sense to use the same fin configuration, say 5 fins/in. fin density, for a superheater as for an evaporator.
Rewriting Eq. (3) based on tube-side area and neglecting other resistances,
L_i A/A
U k, h0z
Using the data from Fig. 8.7, U, values have been computed for different fin densities and for different k, values for the configuration indicated in Table 8.15. The results are shown in Table 8.15. Also shown are the ratio of U, values
Between the 5 and 2 fins/in. designs as well as their surface area.
The following conclusions can be drawn [10].
1. As the tube-side coefficient decreases, the ratio of U, values (between 5 and 2 fins/in.) decreases. With k, = 20, the U, ratio is only 1.11. With
An k, of 2000, the U, ratio is 1.74. What this means is that as k,
Decreases, the benefit of increasing the external surface becomes less attractive. With 2.325 times the surface area we have only 1.11-fold improvement in U,. With a higher k, of 2000, the increase is better,
1.74.
|
H |
20 |
100 |
1000 |
|
N, fins/in. |
2 5 |
2 5 |
2 5 |
|
G, lb/ft2 h |
5591 6366 |
5591 6366 |
5591 6366 |
|
At/A, Zh0 a |
0.01546 0.00867 |
0.01546 0.00867 |
0.01546 0.00867 |
|
Uo |
2.73 1.31 |
7.03 4.12 |
11.21 8.38 |
|
U, |
15.28 17.00 |
39.28 53.55 |
62.66 109 |
|
Ratio U, |
1.11 |
1.363 |
1.74 |
|
Ratio DPg |
1.6 |
1.3 |
1.02 |
|
Calculations based on 2.0 x 0.105 tubes, 29 tubes/row, 6ft long, 0.05 in. thick serrated fins; tubes on 4.0in. square pitch; fin height = 0.75in.; gas flow = 150,000pph; gas inlet temp = 1000° F. A Surface area A, of 2 fins/in. tube = 2.59ft2/ft, and for 5 fins/in., A, = 6.02ft2/ft. |
2. A simple estimation of tube wall temperature can tell us that the higher the fin density, the higher the tube wall temperature will be. For the case of ht = 100, with n = 2, Ut = 39.28, gas temperature = 900°F, and fluid temperature of 600°F,
Heat flux qt = (900 — 600) x 39.28 = 11,784 Btu/ft2 h
The temperature drop across the tube-side film (hi =100) =
11, 784/100= 118°F. The wall temperature = 600 + 118 = 718°F.
With n = 5, U = 53.55, q = 53.55 x 300= 16,065Btu/ft2h. Tube wall temperature = 600 + 16,065/100 = 761°F. Note that we are comparing for the same height. The increase in wall temperature is 43 °F.
3. The ratio of the gas pressure drop between the 5 and 2 fins/in. designs (after adjusting for the effect of U values and differences in surface area for the same energy transfer) increases as the tube-side coefficient reduces. It is 1.6 for ht = 20 and 1.02 for ht = 2000. That is, when ht is smaller, it is prudent to use a smaller fin surface.
The effects of inside and outside fouling factors ffi and ffo are shown in Tables
8.16 and 8.17. The following observations can be made.
1. With a smaller fin density, the effect of ffi is less. With 0.01 fouling
And 2 fins/in., Uo = 6.89 compared with 10.54 with 0.001 fouling. The ratio is 0.65. With 5 fins/in., the corresponding values are 4.01 and
|
Fins/in., n |
2 |
2 |
5 |
5 |
|
Uo, clean |
11.21 |
11.21 |
8.38 |
8.38 |
|
Ff/ |
0.001 |
0.01 |
0.001 |
0.01 |
|
Uo, dirty |
10.54 |
6.89 |
7.56 |
4.01 |
|
Uo as % |
100 |
65 |
100 |
53 |
|
A Tube-side coefficient = 2000. |
7.46, the ratio being 0.53. That means that with increased tube-side fouling it makes sense to use a lower fin density or smaller ratio of external to internal surface area. The same conclusion was reached with a smaller tube-side coefficient.
2. The effect of ffo is less significant, because it is not enhanced by the Ratio of external to internal surface area. A review of Eq. (1) tells us that the tube-side heat transfer coefficient or fouling factor is increased by the ratio of the external to internal surface area, and hence its effect is easily magnified.
Compare the effect of tube-side fouling on bare, low, and high finned tubes.
Three boiler evaporators were designed using bare tubes, 2 fins/in. and 5 fins/in., to cool 150,000 lb/h of clean flue gases from 1000°F to 520°F. The effect of fouling factors of 0.001 and 0.01 on duty, tube wall temperatures, and steam production are shown in Table 8.18. The following points may be observed [11].
1. With bare tubes, the higher tube-side fouling results in the lowest reduction in duty, from 19.65 to 18.65 MM Btu/h, with the exit gas
|
Table 8.17 Effect of ffo, Outside Fouling Factor3
|
|
A Tube-side coefficient = 2000. |
|
Case |
1 |
2 |
3 |
4 |
5 |
6 |
|
1. Gas temp in, °F |
1000 |
1000 |
1000 |
1000 |
1000 |
1000 |
|
2. Exit temp, °F |
520 |
545 |
520 |
604 |
520 |
646 |
|
3. Duty, MM Btu/h |
19.65 |
18.65 |
19.65 |
16.30 |
19.65 |
14.60 |
|
4. Steam flow, lb/h |
19,390 |
18,400 |
19,390 |
16,110 |
19,390 |
14,400 |
|
5. ff,, ft2 h °F/Btu |
0.001 |
0.01 |
0.001 |
0.01 |
0.001 |
0.01 |
|
6. Heat flux, Btu/ft2 h |
9314 |
8162 |
35,360 |
23,080 |
55,790 |
30,260 |
|
7. Wall temp, °F |
437 |
516 |
490 |
680 |
530 |
760 |
|
8. Fin temp, °F |
— |
— |
730 |
840 |
725 |
861 |
|
9. At/A, |
1.13 |
1.13 |
5.6 |
5.6 |
12.3 |
12.3 |
|
10. Fins |
Bare |
Bare |
(2 x 0.75 |
(5 x 0.75 |
||
|
X 0.05 x |
0.157) |
X 0.05 x |
0.157) |
|||
|
11. Tubes per row |
20 |
20 |
20 |
20 |
20 |
20 |
|
12. No. deep |
60 |
60 |
16 |
16 |
10 |
10 |
|
8 |
8 |
8 |
8 |
8 |
8 |
|
|
14. Surface area, ft2 |
5024 |
5024 |
6642 |
6642 |
9122 |
9122 |
|
15. Gas Dp, in. WC |
3.0 |
3.1 |
1.80 |
1.90 |
2.0 |
2.1 |
Temperature going up to 545°F from 520°F—see columns 1 and 2. With 2 fins/in., the exit gas temperature increases from 520°F to 604°F, with the duty reducing to 16.3 from 19.65 MM Btu/h. The steam generation is about 3200 lb/h lower. With 5 fins/in., the reduction in duty and steam generation are the greatest.
2. The heat flux increases with fin density. Therefore, with high temperature units one has to be concerned with DNB conditions; however, heat flux decreases because of fouling.
3. The tube wall temperature increases significantly with fin density. The same fouling factor results in a much higher tube wall temperature for finned tubes than for bare tubes. The tube wall temperature increases from 530°F to 760°F with 5 fins/in., and from 437°F to 516°F for bare tubes. The effect of fouling is more pronounced in tubes of high fin density, which means that high fin density tubes have to be kept cleaner than bare tubes. Demineralized water and good water treatment are recommended in such situations.
How is the weight of solid and serrated fins determined?
A: The weight of fins is given by the formulas
Wf = 10 . 68 x Fbn x (do + h) x (h + 0 . 03) for solid fins Wf = 10 . 68 x Fbndo x (h + 0 .12) for serrated fins
Where
Wf = the fin weight, lb/ft (The segment width does not affect the weight.) b = fin thickness, in. n = fin density, fins/in. h = fin height, in. do = tube outer diameter, in.
Factor F corrects for material of fins and is given in Table 8.19 [9].
The weight oF thE tubes has to be added to the fin weight to give the total weight of the finned tube. Tube weight per unit length is given by
Wt = 10 . 68 x F x dm x tm (68)
Where
Dm = mean diameter of tube, in. tm = average wall thickness, in.
Determine the weight of solid carbon steel fins on a 2 in. OD tube if the fin density is 5 fins/in., height = 0.75 in., and thickness = 0.05 in. Average tube wall thickness is 0.120 in.
|
Table 8.19 Table of F Factors
|
So/wtion. F from Table 8.19 = 1. Using Eq. (67a), we have Wf = 10.68 x 1 x 0.05 x 5 x (2 + 0 .75) x (0.75 + 0.03) = 5 .725 lb/ft The tube weight has to be added to this. The tube weight is given by Wt = 10. 68 x 1.94 x 0.12 = 2.49 lb/ft Hence the total weight of the finned tube = 2.49 + 5.725 = 8.215 lb/ft.
What is the effect of fin thickness and conductivity on boiler performance and tube and fin tip temperatures?
Table 8.20 gives the performance of a boiler evaporator using different fins.
2 x 0.120 carbon steel tubes; 26 tubes/row, 14 deep, 20 ft long 4 x 0.75 x 0.05 thick solid fins; surface area = 35,831 ft2
4 x 0.75 x 0.102 thick solid fins; surface area = 36,426 ft2 In-line arrangement, 4 in. square pitch.
Gas flow = 430,000 lb/h at 1400°F in; vol%, CO2 = 8.2, H2O = 20.9, N2 = 67.51, O2 = 3.1 Steam pressure = 635 psig
Fouling factors = 0.001 ft2h °F/Btu on both gas and steam.
It can be seen that
1. Due to the slightly larger surface area and higher heat transfer coefficient, more duty is transferred with higher fin thickness.
|
Table 8.20 Fin Configuration and Performance
|
2. The overall heat transfer coefficient is increased owing to higher fin effectiveness for the same fin conductivity and greater fin thickness.
3. Lower fin conductivity reduces the fin effectiveness and the overall heat transfer coefficient U, and hence less duty is transferred.
Is surface area an important criterion for evaluating different boiler designs?
The answer is yes if the person evaluating the designs is knowledgeable in heat transfer-related aspects and no if the person simply compares different designs looking only for surface area information. We have seen this in the case of fire tube boilers (Q8.11), where, due to variations in tube size and gas velocity, different designs with over 40-50% difference in surface areas were obtained for the same duty. In the case of water tube boilers also, due to variations in tube size, pitch, and gas velocity, one can have different surface areas for the same duty; hence one has to be careful in evaluating boilers based only on surface areas.
In the case of finned tube boilers, in addition to tube size, pitch, and arrangement (staggered or in-line), one has to review the fin configuration—the height, thickness, and fin density. The higher the fin density or ratio of external to internal surface area, the lower the overall heat transfer coefficient will be even though the surface area can be 100-200% greater. It is also possible to transfer more duty with less surface area by proper selection of fin geometry.
A superheater is to be designed for the conditions shown in Table 8.21. Study the different designs possible with varying fin configurations.
Solution. Using the methods discussed above, various designs were arrived at, with the results shown in Table 8.22 [10]. Several interesting observations can be made. In cases 1 and 2, the same energy of 19.8 MMBtu/h is transferred; however, the surface area of case 2 is much higher because of the high fin density, which decreases U, the overall heat transfer coefficient. Also, the tube wall and fin tip temperatures are higher because of the large ratio of external to internal surface area.
Gas flow = 240,000 Ib/h Gas inlet temperature = 1300°F Gas analysis (vol%)
CO2 = 7 H2O = 12 N2 = 75
O2 = 6
Comparing cases 3 and 4, we see that case 3 transfers more energy with less surface area because of better fin selection. Thus it is not a good idea to select or evaluate designs based on surface area alone, because this can be misleading. In addition, excessive fin surface can lead to higher tube wall and fin tip temperatures, Forcing one to use better materials and increasing the cost. Some purchasing managers believe incorrectly that if they can get more surface area for the same price, they are getting a good deal. Nothing could be further from the truth.
When extended surfaces are used, the choice of fin density is generally arrived at based on optimization studies as illustrated below. Varying the fin density affects
|
Table 8.22 Effect of Fin Geometry on Superheater Performance
|
The gas pressure drop, surface area, and weight of the boiler, not to mention the tube wall and fin tip temperatures. An incineration plant evaporator is to be designed to cool 550,000 lb/h of clean flues gases from 1000°F to about 460°F. Steam pressure is 250 psig sat. Feedwater enters the evaporator at 230°F Flue gas analysis (vol%) is CO2 = 7, H2O = 12, N2 = 75 O2 = 6. Fouling factors are 0.001 ft2 h °F/Btu on both the gas and steam sides. Study the effect of fin configuration on the design.
The calculation procedure for finned tubes is detailed in Q8.19a-Q8.19c. Only the results from using a computer program will be discussed here. Using serrated fins of density 2, 4, and 6 fins/in., 0.75 in. high, 0.05 in. thick with 30 tubes/row,
4 in. square pitch configuration, the lengths were varied to obtain different gas mass velocities. The number of rows deep was adjusted to obtain an exit gas temperature of about 460°F or a duty of about 82MMBtu/h. Figure 8.8 shows the results from the study.
As the gas mass velocity increases we see that the gas pressure drop increases, whereas the surface area decreases for both 2 and 6 fins/in. designs, which should be obvious. The surface area required for the 6 fins/in. design is much larger than with 2 fins/in. As discussed in Q8.27a, the heat transfer coefficient with higher fin density or large external fin surface area is lower. The weight of the tube bundle is also higher with higher fin density.
|
|
Gas mass velocity .1000 lb/ft h Figure 8.8 Effect of fin geometry on HRSG surface area and gas pressure drop.
Table 8.23 summarizes the designs for the 2 and 6 fins/in. cases for the same duty and gas pressure drop of 4in. WC. It is seen that the surface area is much larger with the 6 fins/in. design. The tube wall temperature is also higher due to the higher heat flux, and the weight is slightly more. However, the fabrication cost may be less due to the smaller number of rows deep. Depending on the design, the drum length could also be smaller due to this. One may evaluate these factors and select the optimum design.
As discussed earlier, surface areas from different designs should be interpreted carefully One show/d not select a design based on surface area considerations. With higher fin density, the heat transfer coefficient will be lower and vice versa. Simply looking at a spreadsheet that shows surface areas of tubes of different suppliers and deciding that the design with more surface area is better is technically incorrect. As can be seen below, the higher surface area option has higher tube wall temperature and heat flux inside the tubes. If one wants to compare alternative designs, one should look at UA, the product of overall heat transfer coefficient U and surface area A and not the surface area alone. The equation for energy transfer is Q = UAAT. Q and AT being the same, UA should be constant for the various options. Unless one knows how to calculate the heat transfer coefficients, comparison of surface areas alone should not be attempted, because it can be misleading. Factors such as tube size, spacing, geometry, and fin configuration affect U. The discussion also applies to fire tube boilers, where tube sizes and gas velocities can impact surface areas.
|
Table 8.23 Design of a Boiler with 2 and 6 Fins/in.
|
How are tubular air heaters designed?
Let Wg, and Wa be the gas and air quantities. Normally, flue gas flows inside the tubes while air flows across the tubes in crossflow fashion, as shown in Fig. 8.9. Carbon steel tubes of 1j-3.0in. OD are generally used. Thickness ranges from 0.06 to 0.09 in. because high pressures are not involved. The tubes are arranged in in-line fashion and are connected to the tube sheets at the ends. More than one block may be used in series; in this case, air flows across the tube bundles with a few turns. Hence, while calculating log-mean temperature difference, we must consider correction factors FT.
Flue gas velocity is in the range of 40-70 fps, and air-side mass velocities range from 4000 to 8000 lb/ft2 h. Nw and Nd, the numbers of tubes wide and deep, can be decided on the basis of duct dimensions leading to the air heater. In the case of a separate heater, we have the choice of Nw or Nd. In a boiler, for example, duct dimensions at the economizer section fix dimensions of the air heater also, because the air heater is located below the economizer.
To size the air heater, first determine the total number of tubes Nt [1]:
0 TOC o "1-5" h z. 05Wg, x
N = dvf (69)
ST/d and SL/d range from 1.25 to 2.0. For the gas-side heat transfer coefficient h,, Eq. (12) is used:
H,- = 2 . 44 x w0, 8 ‘ d,1 8
Values of C are evaluated at average flue gas temperature.
The air-side heat transfer coefficient ho is given by Eq. (19) (variation in ho between staggered and in-line arrangements is small in the range of Reynolds number and pitches one comes across),
Ho = 0 . 9 x G06 dF4
The value ho is calculated at air film temperature.
Because the temperature drops across the gas and air films are nearly the same, unlike in an evaporator or superheater, film temperature is approximated as
Tf = (3tg + ta)/4 (70)
|
FIgure 8.9 Tubular air heater. |
Where t and ta refer to the average of gas and air temperatures. Calculate U using
11 TOC o "1-5" h z x d 1
U = h d + ~r (71)
U hidi ho
Metal resistance is neglected. Air-and gas-side pressure drops can be computed
By Eqs. (26) and (28) of Chapter 7, after surfacing is done:
^ o L “t — 5di
APg = 93 x 10-6 x fw2 1
Pgd<5
APair = 9.3 x 10-10 x fG2 —
Pair
It is also good to check for partial load performance to see if dew point corrosion problems are likely. Methods like air bypass or steam-air heating must Be considered. Vibration of tube bundles must also be checked.
C and F are given in Table 8.24 for easy reference.
A quantity of 500,000 lb/h of flue gas from a boiler is cooled from 700°F;
400,0 lb/h of air at 80°F is heated to 400°F. Design a suitable tubular air heater. Carbon steel tubes of 2 in. OD and 0.087 in. thickness are available.
Solution. Assume that duct dimensions are not a limitation. Hence, the bundle arrangement is quite flexible. Choose ST/d = 1.5 and SL/d = 1.25 in. inline; use a maximum flue gas velocity of 50 ft/s.
From an energy balance, assuming negligible losses and for a specific heat of 0.25 for gas and 0.24 for the air side,
Q = 500,000 x 0.25 x (700 — t)
= 400,000 x 0.24 x (400 — 80)
= 30.7 x 106 Btu/h
|
Table 8.24 C and F Factors for Calculating h, and ho of Tubular Air
|
Hence, the gas temperature leaving the air heater is 454°F. The average flue gas temperature is (700 + 454)/2 = 577°F. Let the molecular weight of the flue gas be 30. Then
TOC o "1-5" h z 30 492
Pg =——- x————— = 0.0396 lb/cu ft
359 460 + 577 ‘
From Eq. (69),
= 0.025 x 500,000 =3800
* 1. 8262 x 0.0396 x 50
ST = 3. 0 in., Sl = 2 . 5 in.
Let Nw = 60. Hence, the width of the air heater is
3 0
60 ^ — = 15 ft 12
Nd = 63 because Nt = Nw x Nd, so Depth =63 x 2 . 5/12 = 13. 2 ft At 577°F, from Table 8.24 We have C = 0.178:
„ /500,000°• 8 0 .178
H, = 2 .44 x ———————- x
3780 7 "(1.826)1 8
= 7 .2 Btu/ft2 h °F
To estimate ho, G is required. This requires an idea of L. We must assume a value for the length and check later to see if it is sufficient. Hence, it is a trial-and- error approach. Try L = 15 ft:
St d 1 o
FGA = x NwL = — x 60 x 15 = 75 ft2
12 w 12
G = 400,000/75 = 5333 lb/ft2 h Average gas and air temperatures are
Tg = 577°F, ta = 240°F
T 3 x 577 + 240 = 492°f
|
4 |
(/
Ho = 0.9 x 53330 6 x 0.105/20,4 = 12.3 Btu/ft2h°F
1 1 2.0 1
= — +
U 7.2 1.826 12.3
= 0.152 + 0.081 = 0.233
U = 4.3 Btu/ft2 h °F
We must calculate FT, the correction factor for AT, for the case of one fluid mixed and the other unmixed. From Fig. 8.10 (single-pass crossflow),
„ 700 — 454 „
R = 1ЦЦ-8Ц — = 0.77
400 — 80
P =————— = 0.516
700 — 80
FT = 0.9
Therefore,
AT = 0.9 x(454 — 80)-(70°- 400) = 302°F ln(374/300)
A = ^ = 30.7 X 106 = 23,641ft*
U x AT 4.3 x 302
= — xT — x 3780 L
12
L 11 . 95 ft
Hence, the assumed L is not correct. Try L = 11.0 ft.
FGA = 15 x 75 = 55 ft2
G = 7272 lb/ft2 h
|
|
|
Cornet Ion (actor Correction (actor Cormltcn loctor Corrtction (actor |
|
Figure 8.10 Crossflow correction factors (From Refs. 1 and 2). |
Taking ratios,
—= 1 x Z0 + = 0.152 + 0.067
U 7.2 x 1.826 14.8
= 0.219
U = 4.56 Btu/ft2 h °F
A = 307 x = 22,293 ft2, L = 11.25 ft
4:56 x 302
The calculated and assumed lengths are close to each other, and the design may be frozen. Check the metal temperature at the exit portion. Because the gas — side resistance and air film resistances are 0.152 and 0.067, the metal temperature at the exit of the air heater can be calculated as follows. ThE drop across the gas film will be
0152(454 — 80) = 260°F 0.152 + 0.067
Metal temperature will be 454 — 260 = 194°F.
If the flue gas contains sulfur, dew point corrosion may occur at the exit. The air-side heat transfer coefficient is high, so the drop across its film is low compared to the gas-side film drop. If we increase the flue gas heat transfer coefficient, the drop across its film will be low and the metal temperature will be higher.
How is the off-design performance evaluated?
The air heater described in Q8.28 works at partial loads. Wg =
300,0 lb/h, and flue gas enters the air heater at 620°F. Wa = 250,000 lb/h,
And the air temperature is 80°F. Check the exit gas temperatures of gas and air.
Assume the gas leaves the air heater at 400°F. Then Q = 300,000 x 0.25 x (620 — 400)
= 250,000 x 0.24(t — 80) = 16.5 x 106
Air temperature leaving = 355°F
To calculate h, and ho, see Table 8.24. At an average flue gas temperature
Of (620 + 400)/2 = 510°F, C = 0 .175 . And at a film temperature of
[3 x 510 + (355 + 80)/2]/4 = 437°F, F = 0 .104.
„ /300,000^° . 8 0 .175
H,- = 2 .44 x I———— I x————— t-t
‘ V 3825 / (1.826)1 8
= 4 . 75 Btu/ft2 h °F
G = ^ = 3333 lb/ft2 h
(3333)0,6 2
Ho = 0 • 9 x v 20 4 x 0.104 = 9.22 Btu/ft2 h °F
— =———- 2———- b^— = 0 • 238
U 1.826 x 4.73 9.22
U = 4 . 22 Btu/ft2 h °F From Fig. 8.10,
355 — 80 P = 620-80 = 051 620 — 400 = 355 — 80 = •
FT = 0 . 9
(400 — 80) — (620 — 355)
AT = 0 • 9 x ‘^’ = 262°F
Transferred Q = 4.2 x 262 x 23,640 = 26 x 106 Btu/h, and assumed
Q = 16.5 x 106 Btu/h. They don’t tally.
Since the air heater can transfer more energy, assume a higher air temperature, 390°F, at the exit:
Q = 250,000 x 0.24(390 — 80) = 18 .6 x 106 = 300,000 x 0.25 x (620 — t)
Then gas temperature leaving = 372°F.
Assume U remains the same at 4.2 Btu/ft2 h °F. Then
R = 0 . 8, P = 0.574, FT = 0 . 82
AT = 213°F
Transferred Q = 4.2 x 23,640 x 213 = 21.1 x 106 Btu/h
Again, they don’t tally. Next, try Q = 20 x 106Btu/h.
Air temperature leaving = 410° F Gas temperature leaving = 353°F FT = 0.75, AT = 0.75 x 242 = 182°F
Transferred Q = 4.2 x 23,640 x 182 = 18 x 106 Btu/h
Again, try an exit air temperature at 400°F. Then
Q = 250,000 x 0.24 x (400 — 80)
= 19.2 x 106 Btu/h
19.2 x 106
Exit gas temperature = 620 —
300,0 x 0.25 = 364°F
320
R = 0.8, P = 540 = 0.593, FT = 0.77
284 220
AT = 0.77 x —————— = 193°F
Ln(284/220)
Transferred Q = 4.2 x 193 x 23,640 = 19.16 x 106 Btu/h Q = 19.2 x 106 Btu/h
The gas leaves at 364°F against 454°F at full load.
Metal temperature can be computed as before. At lower loads, metal temperature is lower, and the air heater should be given some protection. This protection may take two forms: Bypass part of the air or use steam to heat the air entering the heater to 100-120°F. Either of these will increase the average metal temperature of the air heater. In the first case, the air-side heat transfer coefficient will fall. Because U decreases, the gas temperature leaving the air heater will increase and less Q will be transferred. Hence, metal temperature will increase. In the second case, air temperature entering increases, so protection of the metal is ensured. Again, the gas temperature differential at the exit will be higher, causing a higher exit gas temperature.
Solve the problem using the NTU method.
Solution. Often the NTU method is convenient when trial-and-error calculations of the type shown above are involved.
NTU = UL = 42 x 23,640 = 1.65 Cmin 250,000 x 0.24
|
= 0.80 |
Cmixed 250,000 x 0.24
C_d 300,000 x 0.25
E = effectiveness C
= 1 — exp{-cms- [1 _ exp(—NTU x C)]}
Cmin (‘2)
= 1 — exp{—1.25[1 — exp(—1.65 x 0.8)]}
= 0.59
Effectiveness = 0.59 =———- —————-
620 — 80
Air temperature rise = 319° F
Air temperature leaving = 319 + 80 = 399°F
This compares well with the answer of 400°F. When U does not change much, this method is very handy.
Predict the exit gas and water temperatures and the energy transferred in an economizer under the following conditions:
Tg1 =gas temperature in = 1000° F tw1 = water temperature in = 250°F A = surface area = 6000 ft2 Wg = gas flow = 75,000 lb/h Ww = water flow = 67,000 lb/h U = overall heat transfer coefficient = 8 Btu/ft2 h °F Cpg = gas specific heat = 0.265 Btu/lb °F Cpw = water specific heat = 1 Btu/lb °F
Figure 8.11 Shows the arrangement of an economizer. A trial-and-error method is usually adopted to solve for the duty of any heat transfer equipment if the surface area is known. This procedure is detailed in Q8.29. Alternatively, the number of transfer units (NTU) method predicts the exit temperatures and duty. For more on
|
|
Q = eCmin(tg1 — tw1) (73)
Where e depends on the type of flow, whether counterflow, parallel flow, or crossflow. In economizers, usually a counterflow arrangement is adopted. e for this is given by
1 — exp [-NTU x (1 — C)]
1 — C exp[-NTU x (1 — C)] ( )
Where
XrrTT UA J ^ (WCP)min
NTU = “ and C = (WC)
^min Vr’ v’^p)max
(WCp)min = 75,000 x 0.265 = 19,875 (WCp)max = 67,000 x 1 = 67,000
C = 19875 = 0.3
67,000
6000
NTU = 8 x————— = 2 . 42
19,875
Substituting into Eq. (74) yields
E = 1 — exp(-2 M x 0- 7) = 0 ,86
1 — 0 . 3 x exp(-2 . 42 x 0 . 7)
From Eq. (73),
Q = 0.86 x 19,875 x (1000 — 250)
= 12 . 8 x 106 Btu/h Let us calculate the exit water and gas temperatures.
Q = WwCpw(tw2 — tw1) = WgCpg(tg1 — tg2)
Hence,
|
= 441°F |
106
Tw2 = 250 + 12. 8 x
67,0 x 1 106
|
Tg2 = 1000 — 12. 8 x — g2 75,000 x 0.265 |
355°F
The NTU method can be used to evaluate the performance of other types of heat transfer equipment, Table 8.25 gives the effectiveness factor e.
Table 8.25 Effectiveness Factors
|
Effectiveness |
Exchanger type
|
2 |
|
C |
|
1 |
|
= |
|
1 — S1 |
|
X NTU0 • 78)- 1]} |
|
NTU + |
|
1 — exp(-NTU x C) Crossflow, stream Cmin unmixed e = C{1 — exp[-C[1 — exp(-NTU)]]} 1 — exp{-C[1 — exp(-NTU x C)]} |
|
Crossflow, stream Cmax unmixed e |
|
Parallel flow, single-pass e -Counterflow, single-pass e — Shell-and-tube (one shell pass; e1 2, 4, 6, etc., tube passes) |
|
Shell-and-tube (n shell passes; 2n, 4n, 6n, etc., tube passes) Crossflow, both streams unmixed Crossflow, both streams mixed |
|
N |
|
1 — exp[-NTU x (1 + C)] 1+C 1 — exp[-NTU x (1 — C)] 1 — C exp[-NTU x (1 — C)] 1 + exp[-NTU x (1 + C2)1/2] |
|
1 — exp[-NTU x (1 + C2)1/2] 1 X (1 + C2)1/2 ‘ 1 — s1Cn |
|
1 — exp{C x NTU0 • 22[exp(-C -1]} NTU |
|
1 — exp(-NTU) NTU x C |
|
1 — e1 C’ 1 — S1 |
|
1 + C + — |
|
1 |
 |
How is the natural or free convection heat transfer coefficient in air determined? A:
The situations of interest to steam plant engineers would be those involving heat transfer between pipes or tubes and air as when an insulated pipe runs across a room or outside it and heat transfer can take place with the atmosphere. Simplified forms of these equations are the following [12].
1. 
Horizontal pipes in air:
(75a)
Where
AT = temperature difference between the hot surface and cold fluid, °F do = tube outside diameter, in.
2. Long vertical pipes:
|
‘AT ’25 |
(75b)
3. Vertical plates less than 2 ft high:
(75c)
|
|
|
|
|
|
|
|
|
|
|
|
|
Determine the heat transfer coefficient between a horizontal bare pipe of diameter 4.5 in. at 500°F and atmospheric air at 80°F.
Solution.
How is the natural or free convection heat transfer coefficient between tube bundles and liquids determined?
One has to determine the free convection heat transfer coefficient when tube bundles such as desuperheater coils or drum preheat coils are immersed in boiler water in order to arrive at the overall heat transfer coefficient and then the surface area. Drum coil desuperheaters are used instead of spray desuperheaters when solids are not permitted to be injected into steam. The heat exchanger is used to cool superheated steam (Fig. 8.12), which flows inside the tubes while the cooler water is outside the tubes in the drum. Drum heating coils are used to keep boiler water hot for quick restart or to prevent freezing.
In this heat exchanger, steam condenses inside tubes while the cooler water is outside the tubes. The natural convection coefficient between the coil and drum water has to be determined to arrive at the overall heat transfer coefficient and then the size or surface area.
The equation that relates hc with other parameters is [2]
|
Figure 8.12 Exchanger inside boiler drum. |
|
|
Where
Do = tube outer diameter, in. k = fluid thermal conductivity, Btu/fth °F C = fluid specific heat, Btu/lb °F p = volumetric expansion coefficient, °R_ 1 AT = temperature difference between tubes and liquid, °F m = viscosity of fluid, lb/ft h p = fluid density, lb/ft3
Fluid properties at saturation conditions are given in Table 8.26.
1 in. pipes are used to maintain boiler water at 100°F in a tank using steam at 212°F, which is condensed inside the tubes. Assume that the pipes are at 200°F, and estimate the free convection heat transfer coefficient between pipes and water.
So/wft’on. From Table 8.26, at a mean temperature of 150°F, k = 0 . 381, m = 1. 04, p = 0.0002, pf = 61. 2
Cp = 1. 0, AT = 100, do = 1. 32
|
|
|
61.22 x 1.0 x 0.0002 x 100 1.04 x 1. 32 |
|
= 188 Btu/ft2 h °F |
8.33
Estimate the surface area of the heat exchanger required to maintain water in a boiler at 100°F using steam at 212°F as in the example of Q8.32. Assume that the heat loss to the cold ambient from the boiler is 0.5MMBtu/h. Steam is condensed inside the tubes. 1 in. schedule 40 pipes are used.
|
F °P J B F |
M (lb/ft h) |
V k (ft2/h) (Btu/h ft °F) |
(ft“/h) |
B (° R-1) |
N |
|||
|
32 |
1.009 |
62.42 |
4.33 |
0.0694 |
0.327 |
0.0052 |
0 CO X 0 |
3 13.37 |
|
40 |
1.005 |
62.42 |
3.75 |
0.0601 |
0.332 |
0.0053 |
0.045 |
11.36 |
|
50 |
1.002 |
62.38 |
3.17 |
0.0508 |
0.338 |
0.0054 |
0.070 |
9.41 |
|
60 |
1.000 |
62.34 |
2.71 |
0.0435 |
0.344 |
0.0055 |
0.10 |
7.88 |
|
70 |
0.998 |
62.27 |
2.37 |
0.0381 |
0.349 |
0.0056 |
0.13 |
6.78 |
|
80 |
0.998 |
62.17 |
2.08 |
0.0334 |
0.355 |
0.0057 |
0.15 |
5.85 |
|
90 |
0.997 |
62.11 |
1.85 |
0.0298 |
0.360 |
0.0058 |
0.18 |
5.13 |
|
100 |
0.997 |
61.99 |
1.65 |
0.0266 |
0.364 |
0.0059 |
0.20 |
4.52 |
|
110 |
0.997 |
61.84 |
1.49 |
0.0241 |
0.368 |
0.0060 |
0.22 |
4.04 |
|
120 |
0.997 |
61.73 |
1.36 |
0.0220 |
0.372 |
0.0060 |
0.24 |
3.65 |
|
130 |
0.998 |
61.54 |
1.24 |
0.0202 |
0.375 |
0.0061 |
0.27 |
3.30 |
|
140 |
0.998 |
61.39 |
1.14 |
0.0186 |
0.378 |
0.0062 |
0.29 |
3.01 |
|
150 |
0.999 |
61.20 |
1.04 |
0.0170 |
0.381 |
0.0063 |
0.31 |
2.72 |
|
160 |
1.000 |
61.01 |
0.97 |
0.0159 |
0.384 |
0.0063 |
0.33 |
2.53 |
|
170 |
1.001 |
60.79 |
0.90 |
0.0148 |
0.386 |
0.0064 |
0.35 |
2.33 |
|
180 |
1.002 |
60.57 |
0.84 |
0.0139 |
0.389 |
0.0064 |
0.37 |
2.16 |
|
190 |
1.003 |
60.35 |
0.79 |
0.0131 |
0.390 |
0.0065 |
0.39 |
2.03 |
|
200 |
1.004 |
60.13 |
0.74 |
0.0123 |
0.392 |
0.0065 |
0.41 |
1.90 |
|
210 |
1.005 |
59.88 |
0.69 |
0.0115 |
0.393 |
0.0065 |
0.43 |
1.76 |
|
220 |
1.007 |
59.63 |
0.65 |
0.0109 |
0.395 |
0.0066 |
0.45 |
1.66 |
|
230 |
1.009 |
59.38 |
0.62 |
0.0104 |
0.395 |
0.0066 |
0.47 |
1.58 |
|
240 |
1.011 |
59.10 |
0.59 |
0.0100 |
0.396 |
0.0066 |
0.48 |
1.51 |
|
250 |
1.013 |
58.82 |
0.56 |
0.0095 |
0.396 |
0.0066 |
0.50 |
1.43 |
|
260 |
1.015 |
58.51 |
0.53 |
0.0091 |
0.396 |
0.0067 |
0.51 |
1.36 |
|
270 |
1.017 |
58.24 |
0.50 |
0.0086 |
0.396 |
0.0067 |
0.53 |
1.28 |
|
280 |
1.020 |
57.94 |
0.48 |
0.0083 |
0.396 |
0.0067 |
0.55 |
1.24 |
|
290 |
1.023 |
57.64 |
0.46 |
0.0080 |
0.396 |
0.0067 |
0.56 |
1.19 |
|
300 |
1.026 |
57.31 |
0.45 |
0.0079 |
0.395 |
0.0067 |
0.58 |
1.17 |
|
350 |
1.044 |
55.59 |
0.38 |
0.0068 |
0.391 |
0.0067 |
0.62 |
1.01 |
|
400 |
1.067 |
53.65 |
0.33 |
0.0062 |
0.384 |
0.0068 |
0.72 |
0.91 |
|
450 |
1.095 |
51.55 |
0.29 |
0.0056 |
0.373 |
0.0066 |
0.93 |
0.85 |
|
500 |
1.130 |
49.02 |
0.26 |
0.0053 |
0.356 |
0.0064 |
1.18 |
0.83 |
|
550 |
1.200 |
45.92 |
0.23 |
0.0050 |
0.330 |
0.0060 |
1.63 |
0.84 |
|
600 |
1.362 |
42.37 |
0.21 |
0.0050 |
0.298 |
0.0052 |
— |
0.96 |
The overall heat transfer coefficient can be estimated from
TT = ~T + 7 + Rm + ffi + ffo
Uo hn hi
Where Rm = metal resistance, and ff, and ffo are inside and outside fouling factors; see Eq. (3).
Ho, the free convection heat transfer coefficient between the tubes and boiler water, obtained from Q8.32,= 188Btu/ft2h°F. Assume h, = 1500, ff, = ffo =
0. 001, and
D„ d„
Metal resistance = —— ln — = 0.0005 24K d,-
Then
TT = d* + + 0.0025 = 0.00849
Or
Uo = 177 Btu/ft 2 h °F
AT = log-mean temperature difference = 212 — 100 = 112°F
Then,
Q 500,000 2
Surface area A = ——— = ———- —— = 38 ft
Uo AT 11^ x 112
Can we determine gas or steam temperature profiles in a heat recovery steam generator (HRSG) without actually designing it?
Yes. One can simulate the design as well as the off-design performance of an HRSG without designing it in terms of tube size, surface area, etc. The methodology has several applications. Consultants and plant engineers can determine for a given set of gas inlet conditions for an HRSG how much steam can be generated and what the gas/steam temperature profile will look like, and hence write better specifications for the HRSG or select auxiliaries based on this simulation without going to a boiler firm for this information. Thus several options can be ruled out or ruled in depending on the HRSG performance. The methodology has applications in complex, multipressure cogeneration or combined cycle plant evaluation with gas turbines. More information on HRSG simulation can be found in Chapters 1 and 3 and Refs. 11, 12.
140,0 lb/h of turbine exhaust gases at 980°F enter an HRSG generating saturated steam at 200psig. Determine the steam generation and temperature profiles if feedwater temperature is 230°F and blowdown = 5%. Assume that average gas specific heat is 0.27 at the evaporator and 0.253 at the economizer.
Two important terms that determine the design should be defined here (see Fig. 8.13). Pinch ^oi’nt is the difference between the gas temperature leaving the evaporator and saturation temperature. Approach ^o/nt is the difference between the saturation temperature and the water temperature entering the evaporator. More information on how to select these important values and how they are influenced by gas inlet conditions is discussed in examples below.
For unfired gas turbine HRSGs, pinch and approach points lie in the range of 15-30°F. The higher these values, the smaller will be the boiler size and cost, and vice versa.
Let us choose a pinch point of 20°F and an approach point of 15°F. Saturation temperature = 388°F. Figure 8.14 shows the temperature profile. The gas temperature leaving the evaporator = 388 + 20 = 408°F, and water temperature entering it = 388 — 15 = 373°F.
Evaporator duty = 140,000 x 0.99 x 0.27 x (980 — 408) = 21. 4 MMBtu/h
(0.99 is the heat loss factor with a 1% loss.)
Enthalpy absorbed by steam in evaporator
= (1199.3 — 345) + 0.05 x (362.2 — 345)
= 855 .2 Btu/lb
(1199.3, 345, and 362.2 are the enthalpies of saturated steam, water entering the evaporator, and saturated water, respectively. 0.05 is the blowdown factor for 5% blowdown.)
|
T01
Twl Figure 8.13 Pinch and approach points. |
|
900 »Laon Flow ■ 10.610 lb/l-i 943
240 Figure 8.14 Temperature profile in an HRSG. |
21.4 x 106
Steam generated = —-—-— = 25,000 lb/h
855.2
Economizer duty = 25,000 x 1.05 x (345 — 198.5)
= 3.84 MM Btu/h
^ + + , 3,840,000
Gas temperature drop =————————
F F 140,000 x 0.253 x 0.99
= 109°F
Hence gas temperature leaving economizer = 408 — 109 = 299°F. Thus the thermal design of the HRSG is simulated.
Simulate the performance of the HRSG designed in Q8.34 when a gas flow of
165,0 lb/h enters the HRSG at 880°F. The HRSG will operate at 150psig. Feedwater temperature remains at 230°F.
Gas turbine exhaust flow and temperature change with ambient conditions and load. As a result the HRSG has to operate at different gas parameters, and hence simulation is necessary to determine how the HRSG behaves under different gas and steam parameters.
The evaporator performance can be determined by using Eq. (37). Based on design conditions, compute K.
|
980 — 388′ |
|
In |
|
408 — 388 K = 387 . 6 |
|
= K x (140,000)-0 4 = 3. 388 |
 |
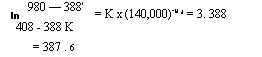Under the new conditions, 880 — 366
|
In |
= 387 . 6 x (165,000)-04 = 3.1724
Tg2 — 366
Hence tg2 = 388°F.
Evaporator duty = 165,000 x 0.99 x 0.27 x (880 — 388)
= 21. 70 MMBtu/h
In order to estimate the steam flow, the feedwater temperature leaving the economizer must be known. This is arrived at through a series of iterations. Try tw2 = 360°F. Then
21 70 106
Steam flow
(1195 . 7 — 332) + 0 .05 x (338 . 5 — 332)
= 25,110 lb/h
Economizer assumed duty Qa = 25,110 x 1. 05
X (332 — 198 . 5)
= 3. 52 MMBtu/h
Compute the term (US)design = Q/AT for the economizer based on design conditions.
Q = 3. 84 x 106
^ (299 — 230) —(408 — 373) ^
AT =—————— ^69/35)—————- = 50 F
Hence (US)design = 3,840,000/50 = 76,800. Correct this for off-design conditions.
(USV = <us. W x (ggfiпefF
/165,000
= 76,800 x ——— ^—- = 85,200
1 140,000 ‘
The economizer transferred duty is then (US)perf x AT. Based on 360°F water leaving the economizer, Qa = 3.52 MBtu/h and the exit gas temperature is
Tg2 =_____ 3,520,000________ = 85°F
G2 165,000 x 0.99 x 0.253
Hence tg2 = 388 — 85 = 303°F, and
(303 — 230) — (388 — 360) _ 4y°F ln(73/28)
Transferred duty Qt = 85,200 x 47 = 4.00 MM Btu/h
Because the assumed and transferred duty do not match, another iteration is required. We can show that at duty of 3.55 MM Btu/h the, assumed and transferred duty match. Water temperature leaving the economizer = 366°F (saturation); exit gas temperature = 301°F. Steam generation = 25,310lb/h.
Because the calculations are quite involved, I have developed a software program called HRSGS that can simulate the design and off-design performance of complex, multipressure fired and unfired HRSGs. More information can be had by writing to V Ganapathy, P. O. Box 673, Abilene, TX 79604.
In the above case, how much fuel is required and at what firing temperature if
35,0 lb/h steam at 200psig is to be generated? Gas flow is 140,000 lb/h at 980°F as in Q8.35a.
A simple solution is given here, though the HRSG simulation would provide more accurate evaluation and temperature profiles. We make use of the concept that the fuel efficiency is 100% and all of that goes to generating the additional steam as discussed earlier.
Energy absorbed by steam = 35,000 x (1199.3 — 198.5)
= 35.1 MM Btu/h
Additional energy to be provided by the burner = 35.1 — 25.24 = 9.86 MM Btu/h (the HRSG absorbs 25.24 as shown in Q8.34).
The oxygen consumed in the process of combustion (see Q6.27) is
9.86 x 106/(140,000 x 58.4) = 1.2%
9.86 x 106 = 140,000 x 0.3 x (T — 980)
Or
T = 1215°F
Thus, by using a few simple concepts, preliminary information about the HRSG
May be obtained. However, a complete temperature profile analysis requires a
Computer program such as the HRSG simulation software.
8.36 Q:
Can we assume that a particular exit gas temperature can be obtained in gas turbine HRSGs without doing a temperature profile analysis?
No. It is not good practice to assume the HRSG exit gas temperature and compute the duty or steam generation as some consultants and engineers do. The problem is that, depending on the steam pressure and temperature, the exit gas temperature will vary significantly. Often, consultants and plant engineers assume that any stack gas temperature can be achieved. For example, I have seen catalogs published by reputable gas turbine firms suggesting that 300°F stack gas temperature can be obtained irrespective of the steam pressure or parameters. Now this may be possible at low pressures but not at all steam conditions. In order to arrive at the correct temperature profile, several heat balance calculations have to be performed, as explained below.
It will be shown that one cannot arbitrarily fix the stack gas temperature or the pinch point.
Looking at the superheater and evaporator of Fig. 8.13,
TOC o "1-5" h z Wg x Cpg x (Tg1 — Tg3) = Ws x (hso — hw2) (78)
Looking at the entire HRSG,
Wg x Cpg x (Tg — Tg4) = Ws x (hs0 — hwl) (79)
Blowdown was neglected in the above equations for simplicity. Dividing Eq. (78) by Eq. (79) and neglecting variations in Cpg, we have
Tg1 — Tg3 = hs0 — hw2 = X (80)
Tg1 — Tg4 hs0 — hw1
Factor X depends only on steam parameters and on the approach point used. Tg3 depends on the pinch point selected. Hence if Tg1 is known, Tg4 can be calculated.
It can be concluded from the above analysis that one cannot assume that any HRSG exit gas temperature can be obtained. To illustrate, Table 8.27 shows several operating steam conditions and X values and exit gas temperatures. As the steam pressure or steam temperature increases, so does the exit gas temperature, with the result that less energy is transferred to steam. This also tells us why we need to go in for multiple-pressure-level HRSGs when the main steam pressure is high. Note that even with infinite surface areas we cannot achieve low temperatures, because this is a thermodynamic limitation.
Determine the HRSG exit gas temperature when the gas inlet temperature is 900°F and the steam pressure is 100psig sat.
So/wt/on. X = 0.904. Saturation temperature = 338°F. Hence with a 20°F pinch point, Tg3 = 358°F, and tw2 = 323°F with a 15°F approach point,
900 — Tg4
——— g4 = 0.904, or Tg4 = 300°F
900 — 358 g4
What is Tg4 when steam pressure is 600psig and temperature is 750°F?
|
TABLE 8.27 HRSG Exit Gas Temperaturesa
|
|
ABased on 15°F approach point, 20°F pinch point, 900°F gas inlet temperature, and no blowdown. Feedwater temperature is 230°F. Similar data can be generated for other conditions. |
Solution. X = 0.7728. Saturation temperature = 492°F; tw2 = 477°F;
Tg3 = 512°F.
900 — 512
900—= 0.7728, or Tg4 = 398°F
So a 300°F stack temperature is not thermodynamically feasible. Let us see what happens if we try to achieve that.
Can you obtain a 300°F stack gas temperature with 900°F inlet gas temperature and at 600psig, 750°F, and 15°F approach temperature?
Solution. X = 0.7728. Let us see, using Eq. (80), what Tg3 results in a Tg4 of 300°F, because that is the only unknown.
(900 — Tg3)/(900 — 300) = 0.7728, or Tg3 = 436°F
Which is not thermodynamically feasible because the saturation temperature at 615psig is 492°F! This is the reason one has to be careful in specifying HRSG exit gas temperatures or computing steam generation based on a particular exit gas temperature.
What should be done to obtain a stack gas temperature of 300°F in the situation described in Example 3?
Solution. One of the options is to increase the gas inlet temperature to the HRSG by supplementary firing. If Tg1 is increased, then it is possible to get a lower Tg4. Say Tg1 = 1600°F. Then
1600 — Tg3
1600—31 = 0J728, or Tg3 = 595°F
This is a feasible temperature because the pinch point is now (595 — 492) = 103°F. This brings us to another important rule: Pinch point and exit gas temperature cannot be arbitrarily selected in the fired mode. It is preferable to analyze the temperature profiles in the unfired mode and evaluate the off-design performance using available simulation methods discussed earlier.
If gas inlet temperature in Example 1 is 800°F instead of 900°F, what happens to the exit gas temperature at 100psig sat?
So/wft’on.
800 — 358 800 — Tg4
Or Tg4 = 312°F versus the 300°F when the inlet gas temperature was 900°F. We note that the exit gas temperature increases when the gas inlet temperature decreases, and vice versa. This is another important basic fact.
How can HRSG simulation be used to optimize gas and steam temperature profiles?
HRSG simulation is a method of arriving at the design or off-design performance of HRSGs without physically designing them as shown in Q8.34. By using different pinch and approach points and different configurations, particularly in multipressure HRSGs, one can maximize heat recovery. We will illustrate this with an example [12].
A gas turbine exhausts 300,000 lb/h of gas at 900°F. It is desired to generate about 20,500 lb/h of superheated steam at 600psig and 650°F and as much as 200psig saturated steam using feedwater at 230°F. Using the method discussed in Q8.34, we can arrive at the gas/steam temperature profiles and steam flows. Figure 8.15 Shows results obtained with HRSGS software. In option 1, we have the high pressure (HP) section consisting of the superheater, evaporator, and economizer followed by the low pressure (LP) section consisting of the LP evaporator and economizer. By using a pinch point of 190°F and approach point of 15°F, we generate 20,438 lb/h of high pressure steam at 650°F. Then, using a pinch point of 20°F and approach point of 12°F, we make 18,670 lb/h low pressure steam. The stack gas temperature is 370°F. In option 2, we have the HP section consisting of the superheater and evaporator and the LP section consisting of only the evaporator. A common economizer feeds both the HP and LP sections with feedwater at 375°F. Because of the larger heat sink available beyond the LP evaporator, the stack gas temperature decreases to 321 °F. The HP steam generation is adjusted using the pinch point to make 20,488 lb/h while the LP steam is allowed to float. With a pinch point of 20°F, we see that we can make
|
Figure 8.15 Optimizing temperature profiles. |
22,400 lb/h in comparison with the 18,673 lb/h earlier. The ASME system efficiency is much higher now. Thus by manipulating the HRSG configuration, one can maximize the heat recovery.
How is the HRSG efficiency determined according to ASME Power Test Code 4.4?
The efficiency E is given by
Energy given to steam/water/fluids
E = —
Gas flow x inlet enthalpy + fuel input on LHV basis
To evaluate the efficiency, the enthalpy of the turbine exhaust gas should be known. The Appendix gives the enthalpy based on a particular gas analysis. Fuel input on LHV basis should also be known if auxiliary firing is used.
In Q8.37 the efficiency in the design case is
(21. 4 + 3. 84) x 106
E = (————- )—— = 0 . 715, or 71. 5%
140,0 x 242
If steam or water injection is resorted to, then the gas analysis will change, and the enthalpy has to be computed based on the actual analysis.
The HRSG system efficiency in gas turbine plants will improve with the addition of auxiliary fuel, which increases the gas temperature to the HRSG and hence increases its steam generation. There are two reasons for this.
1. Addition of auxiliary fuel reduces the effective excess air in the exhaust gases, because no air is added, only fuel. Hence the exhaust gas loss in relation to steam production is reduced.
2. With increased steam generation, usually the HRSG exhaust gas temperature decreases. This is due to the increased flow of water in the economizer, which offers a larger heat sink, which in turn pulls down the gas temperature further. In gas turbine units, the gas flow does not vary much with steam output as in conventional steam generators, which accounts for the larger temperature drop.
More information on HRSG temperature profiles can be found in Chapters
1 and 2.
Table 8.28 shows the performance of an HRSG under various operating conditions. Case 1 is the unfired case; cases 2 and 3 have different firing conditions. It can be seen that the system efficiency is higher when more fuel is fired, for reasons explained above.
|
TABLE 8.28 Data for Supplementary-Fired HRSG
|
In some cogeneration plants with gas turbines, a forced draft fan is used to send atmospheric air to the HRSG into which fuel is fired to generate steam when the gas turbine is not in operation. What should the criteria be for the fan size?
The air flow should be large enough to have turbulent flow regimes in the HRSG and at the same time be small enough to minimize the loss due to exiting gases. If the air flow is high, the firing temperature will be low, but the system efficiency will be lower and the fuel input will be higher. This is illustrated for a simple case of two fans generating 250,000 and 210,000 lb/h of air flow in the HRSG. The HRSGS program was used in the simulation. See Table 8.29.
How is the performance of an HRSG determined in fresh air fired mode?
In this example, a multiple pressure HRSG with a common economizer is simulated in the design unfired mode and we are predicting its performance in the fired mode with fresh air firing using the HRSGS program.
|
TABLE 8.29 Fresh Air Firing Performance
|
|
Supfttrt svapl supbtrt evap2 6con3 &vap4 Figure 8.16a Unfired multipressure HRSG temperature profile. |
HRSG PERFORMANCE — Off-Design case tЯTЯtl Ц
|
Evap |
Sh evap sh svap eco
Project — 3preshrsg Units* BRITISH Case — fresh air Remarks-
Amb temp — F= 90 heat l0SS‘%= 1 gas temp to HRSG F~ 90 gas flow — Lb/h= 975000 % voI C02 =, H20 = 1, N2 =78 02-21. 302-. ASME eff-% =04.53 tot duty-MM Btu/h=279,4
|
|
Duty pres MMB/h psia 323 36 0 1667 615 133.57 655.8 7.45 215. 00.22 227.5 2905 700 12.47 25. |
|
Surf Bum Sh Evap Sh Evap Eco Evap |
|
Gas temp wat/stm 90 1306 0 0 1308 124S 496 639 124B 754 337 496 754 726 392 528 726 414 337 392 414 299 220 337 299 249 120 239 Staek gas flow =S900&3 %C02=2.71 H20=G 29 N2=75 92 02=15 07 S02= Fuel oas. vol % Rnethane= 97 swiane= 2 propane= 1 LHV — Blufcu ft = 942 LHV — Slu/lb =51430 вug air — l_Wh= Ы |
 |
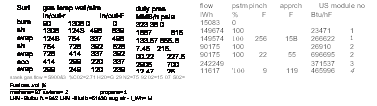‘S2.B
‘414
337
SuphUl evapl suphtr2 evap2 econ3
Figure 8.16b Fresh air fired temperature profile.
Few complex iterations. Figure 8.16a Shows the design mode results from the HRSGS program.
In the off-design or fired mode, fresh air is used instead of turbine exhaust. The air flow used is close to the design exhaust gas flow. We input the ambient air flow and the desired HP steam flow, and the program asks for fuel analysis and automatically arrives at the firing temperature. The off-design performance is shown in Fig. 8.16b.
The efficiency according to ASME Power Test Code 4.4, US values of each surface in both the design and off-design modes may also be seen, as well as the exhaust gas analysis after combustion.
This is yet another example of how simulation may be used to perform various studies without a physical design of an HRSG. Consultants and planners of cogeneration or combined cycle projects should find this a valuable tool.
8.40 Q:
How do we evaluate alternative HRSG designs if the operating costs are different? A:
Let us consider the design of two HRSGs, one with low pinch and approach points (and hence more surface area and gas pressure drop), called design A, and another with higher pinch and approach points, called design B, which costs less. These HRSGs operate in both unfired and fired modes for 50% of the time. In the fired mode, both HRSGs generate 70,000 lb/h of steam; in the unfired mode, design A naturally generates more steam. Table 8.30 shows the performance of the HRSGs in unfired and fired modes.
Let fuel cost $3/MMBtu (LHV). Cost of steam = $3.5/1000lb and electricity = 6 cents/kWh. Assume that an additional 4in. WC of gas pressure drop is equivalent to a 1% decrease in gas turbine power output, which is a nominal 8000 kW. The HRSG operates in unfired and fired modes for 4000 h/y each.
Design A has the following edge over design B in operating costs.
Due to higher steam generation in unfired mode:
(50,000 — 47,230) x 3 x 4000 = $33,240
Due to lower fuel consumption:
(22.55 — 19.23) x 3.5 x 4000 = $46,480
|
Gas temp to HRSG |
980 |
1208 |
980 |
1248 |
|
Gas temp to economizer, °F |
437 |
441 |
466 |
483 |
|
Exit gas temperature, °F |
314 |
298 |
353 |
343 |
|
Gas pressure drop, in. WC |
4. |
0 4.3 |
2. |
75 3 |
|
Steam flow, lb/h |
50,000 |
70,000 |
47,230 |
70,000 |
|
Water temp to economizer, °F |
398 |
373 |
396 |
370 |
|
Burner duty, Mm Btu/h |
0 |
19.23 |
0 |
22 |
|
Evaporator surface area ft2 |
39,809 |
27,866 |
||
|
Economizer surface area, ft2 |
24,383 |
13,933 |
||
|
Pinch point, °F |
16 |
20 |
45 |
62 |
|
23 |
48 |
25 |
51 |
|
Gas flow = 287,000 lb/h; Gas analysis (vol%) CO2 = 3, H2O = 7, N2 = 75, O2 = 15. Steam pressure = 300psig sat; gas turbine power = 8000 kW. |
Due to higher gas pressure drop of 1.3 in. WC:
8000
1.3 x 8000 x 0.07 x——— = $14,560
100 x 4
Thus the net benefit of using design A over B is $(33,240 + 46,480 — 14,560) = $65,160 per year.
If the additional cost of design A over B due to its size is, say, $50,000, the payback of using design A is less than 1 year. However, if the HRSG operates for less than, say, 3000h/year, the payback will be longer and has to be reviewed.
What is steaming, and why is it likely in gas turbine HRSGs and not in conventional fossil fuel fired boilers?
When the economizer in a boiler or HRSG starts generating steam, particularly with downward flow of water, problems can arise in the form of water hammer, vibration, etc. With upward water flow design, a certain amount of steaming, 35%, can be tolerated because the bubbles have a natural tendency to go upward along with the water. However, steaming should generally be avoided.
|
Table 8.31 Typical Exhaust Gas Flow, Temperature Characteristics of a Gas Turbine
|
|
Fuel: natural gas; elevation: sea level; relative humidity 60%; inlet loss 4in. H2O; exhaust loss 15 in. H2O; speed: 3600 rpm; output terminal: generator. |
To understand why the economizer is likely to steam, we should first look at the characteristics of a gas turbine as a function of ambient temperature and load (see Tables 8.31 and 1.4).
In single-shaft machines, which are widely used, as the ambient temperature or load decreases, the exhaust gas temperature decreases. The variation in mass flow is marginal compared to fossil fuel fired boilers, while the steam or water flow drops off significantly. (The effect of mass flow increase in most cases does not offset the effect of lower exhaust gas temperature.) The energy- transferring ability of the economizer, which is governed by the gas-side heat transfer coefficient, does not change much with gas turbine load or ambient temperature; hence nearly the same duty is transferred with a smaller water flow through the economizer, which results in a water exit temperature approaching saturation temperature as seen in Q8.35. Hence we should design the economizer such that it does not steam in the lowest unfired ambient case, which will ensure that steaming does not occur at other ambient conditions. A few other steps may also be taken, such as designing the economizer [8] with a horizontal gas flow with horizontal tubes (Fig. 8.17). This ensures that the last few rows of the economizer, which are likely to steam, have a vertical flow of steam-water mixture.
In conventional fossil fuel fired boilers the gas flow decreases in proportion to the water flow, and the energy-transferring ability of the economizer is also lower at lower loads. Therefore steaming is not a concern in these boilers; usually the approach point increases at lower loads in fired boilers, whereas it is a concern in HRSGs.
The other measures that may be considered to minimize steaming in an economizer are
|
FIgure 8.17 Horizontal gas flow economizer. |
Increase the water flow through the economizer during these conditions by increasing the blowdown flow. This solution works only if small amounts of steam are formed and the period of operation in this mode is small. Blowdown results in a waste of energy.
Increasing the inlet gas temperature either by supplementary firing or by increasing the turbine load helps to generate more steam and thus more water flow through the economizer, which will prevent steaming. As we saw in Chapter 1, the economizer steams at low loads of the turbine.
Exhaust gases can be bypassed around the HRSG during such steaming conditions. This minimizes the amount of energy transferred at the economizer as well as the evaporator. Gas can also be bypassed around the economizer, mitigating the steaming concerns.
Water can also be bypassed around the economizer during steaming conditions, but this is not a good solution. When the gas turbine load picks up, it will be difficult to put the water back into the economizer while the tubes are hot. The cold water inside hot tubes can flash and cause vibration and thermal stresses and can even damage the economizer tub.
Why are water tube boilers generally preferred to fire tube boilers for gas turbine exhaust applications?
Fire tube boilers require a lot of surface area to reduce the temperature of gas leaving the evaporator to within 15-25°F of saturation temperature (pinch point). They have lower heat transfer coefficients than those of bare tube water tube boilers (see Q8.10), which do not compare well with finned tube boilers. Water tube boilers can use extended surfaces to reduce the pinch point to 15-25 °F in the unfired mode and hence be compact. The tubes will be very long if fire tube boilers are used; hence the gas pressure drop will be higher. (A fire tube boiler can be made into a two-pass boiler to reduce the length; however, this will increase the shell diameter and the labor cost, because twice the number of tubes will have to be welded to the tube sheets.) The fire tube boiler will have to be even larger if the same gas pressure drop is to be maintained. Table 8.32 compares the performance of water tube and fire tube boilers for the same duty and pressure drop.
It can be seen from the table footnotes that the water tube boiler is very compact. If the gas flow is very small, say less than 50,000 lb/h, then a fire tube boiler may be considered.
|
Table 8.32 Water Tube vs. Fire Tube Boiler for Gas Turbine Exhaust
AWater tube boiler: 2 x 0.105 in. tubes, 20 wide, 18 deep, 6 ft long, with 5 serrated fins/in., 0.75in. high, 0.05in. thick. BFire tube boiler: 1400 1.5 x 0.105 in. tubes, 21 ft long. |
Does the addition of 10% surface area to a boiler increase its duty by 10%?
No. The additional surface area increases the duty only slightly. The increased temperature drop across the boiler and the temperature rise of water or steam (if single-phase) due to the higher duty results in a lower log-mean temperature difference. This results in lower transferred duty, even assuming that the overall heat transfer coefficient U remains unchanged. If the larger surface area results in lower gas velocities, the increase in duty will be marginal as U is further reduced.
As an example, consider the performance of a fire tube boiler with 10% and 20% increase in surface area as shown in Table 8.33. As can be seen, a 10% increase in surface area increases the duty by only 3%, and a 20% increase in surface area increases the duty by only 6%. Similar trends may be shown for water tube boilers, superheaters, economizers, etc.
How do we estimate the time required to heat a boiler?
A boiler can take a long time to heat up, depending on the initial temperature of the system, mass of steel, and amount of water stored. The following procedure gives a quick estimate of the time required to warm up a boiler. The methodology is applicable to either fire tube or water tube boilers.
|
Table 8.33 Boiler Performance with Increased Surface Areaa
|
|
AGas flow = 70,000lb/h; inlet gas temperature = 1600°F. Gas analysis (vol%): CO2 = 7, H2O = 12, N2 = 75, O2 = 6; steam pressure = 125psig saturated. Tubes: 2 x 0.120 carbon steel. |
Gas at a temperature of Tgj enters the unit, which is initially at a temperature of t1 (both the water and the boiler tubes). The following energy balance equation can then be written neglecting heat losses:
Dt
|
(81) |
Mc — = WgCpg x (Tgl — Tg2) = UADT
Where
Mc = water equivalent of the boiler
= mass of steel x specific heat of steel + mass of water x specific heat of water (Weight of the boiler tubes, drum, casing, etc., is included in the steel weight.) dt/dz = rate of change of temperature, °F/h Wg = gas flow, lb/h Cpg = gas specific heat, Btu/lb °F 1; Tg2 = entering and exit boiler gas temperature, °F U = overall heat transfer coefficient, Btu/ft2h °F A = surface area, ft2 DT = log-mean temperature difference, °F
_ (Tg1 — t) ~ (Tg2 — t)
Ln[(Tgj — t)/(Tg2 — t)]
T = temperature of the water/steam in boiler, °F From Eq. (81) we have
UA
|
(82) |
|
Ln |
|
C R g Pg |
Tgi — t Tg2 — t
Or
TGi — t Tgi — t
|
(83) |
T — t 4- G1_______ — t -L. G1
TG2 _ t ^ eUA=WgCpg _ t ^ K
Substituting Eq. (83) into Eq. (81), we get
|
K — 1 K |
McDZ=WgCpg (Tgi—t)
Or
|
K |
|
VgCpg K — 1 G p^————— dz |
|
Mc |
 |
|
|
|
|
|
|
|
To estimate the time to heat up the boiler from an initial temperature t1 to t2, we have to integrate dt between the limits t1 and t2.
= WgCpg x(K ~ 1)z (85}
-12 Mc K y 5
The above equation can be used to estimate the time required to heat the boiler from a temperature of tj to t2, using flue gases entering at TgX. However, in order to generate steam, we must first bring the boiler to the boiling point at atmospheric pressure and slowly raise the steam pressure through manipulation of vent valves, drains, etc; the first term of Eq. (81) would involve the term for steam generation and flow in addition to metal heating.
A water tube waste heat boiler of weight 50,000 lb and containing 30,000 lb of water is initially at a temperature of 100°F. 130,000 lb of flue gases at 1400°F enter the unit. Assume the following:
Gas specific heat = 0.3 Btu/lb °F
Steel specific heat = 0.12 Btu/lb °F
Surface area of boiler = 21,000 ft2
Overall heat transfer coefficient = 8 Btu/ft2h °F
Estimate the time required to bring the boiler to 212°F.
Solution.
U 8 x 21,000
= 4.3
VgCpg 130,000 x 0.3
K = e4’3 = 74
Mc = 50,000 x 0.12 + 30,000 x 1 = 36,000
TOC o "1-5" h z, 1400 — 100 _ 130,000 x 0.3 73
Ln———— = 0.09 =—————— x —z
1400 — 212 36,000 74
or z = 0.084 h = 5.1 min.
One could develop a computer program to solve Eq. (81) to include steam generation and pressure-raising terms. In real-life boiler operation, the procedure is corrected by factors based on operating data of similar units.
It can also be noted that, in general, fire tube boilers with the same capacity as water tube boilers would have a larger water equivalent and hence the start-up time for fire tube boilers would be longer.
Assuming that the superheater in Q8.19c is dry, how long does it take to heat the metal from 80°F to 900°F? Assume that the gas-side heat transfer coefficient is 12Btu/ft2h °F. Gas flow and temperature are the same as before. The weight of the superheater is 5700 lb. 150,000 lb/h of exhaust gases enter the superheater at 1030°F.
A:
|
GCp (K — 1)z |
|
Tg1 — t 1 |
|
Tg1 — t 2 |
|
Mc x K |
|
Let us use Eq. (85), t1 W |
|
Ln |
 |
|||||||
|
|||||||
|
|||||||
|
|||||||
|
|||||||
Mc = 5700 x 0.12 = 684
, 1030 — 80 150,000 x 0.286 x 0.76z „
Ln—————- =——- —————————— = 27z = 1.99
|
Or |
1030 — 900 1.76 x 684
Z = 0.0737 h = 4.5 min
This is an estimate only but gives an idea of how fast the metal gets heated up. This is important in gas turbine plants without a gas bypass system. A large quantity of exhaust gases can increase the metal temperatures quickly. Hence if frequent start-ups and shutdowns are planned, a stress analysis is required to ensure that critical components are not subjected to undue stresses due to quick changes in tube wall or header temperatures.
By the same token, the superheater tubes cool fast when the exhaust gas is shut off compared to, say, evaporator tubes, which are still hot due to the inventory of hot saturated liquid. This can lead to condensation of steam when the HRSG is restarted, leading to blockage of flow inside the superheater tubes unless adequate drains are provided.
8.44c
Q:
A large mass of metal and water inventory in a boiler results in a longer start-up period, but the residual energy in the metal also helps to respond to load changes faster when the heat input to the boiler is shut off. Drum level fluctuations also are
Smoothed out by a large water inventory. In order to understand the dynamics, let us look at an evaporator in a waste heat boiler with the following data:
Gas flow = 350,000 lb/h Gas inlet temp = 1000°F Gas exit temp = 510°F Steam pressure = 600 psig sat Feedwater temp = 222°F
Tubes: 2 x 0.105, 30 tubes/row, 20 deep, 12 ft long with 4.5 x 0.75 x
0. 05 in. serrated fins Steam drum = 54 in., mud drum = 36 in; both are 13 ft long. Boiler generates 45,000 lb/h of steam.
Weight of steel including drums = 75,000 lb Weight of water in evaporator = 18,000 lb Volume of steam space = 115 ft3 Feedwater temperature = 220°F
Energy transferred by gas to evaporator = 45.9MMBtu/h
What happens to the steam pressure and steam generation when the heat input and the feedwater supply are turned off?
The basic equation for energy transfer to an evaporator is
Q = Wshfg + (hi — hf)Wf + [wmCp — + Wwdpj dp (86a)
Where
Wm = mass of metal, lb Ws = steam generated, lb/h Wf = feedwater flow, lb/h
Ww = amount of water inventory in boiler system including drums, tubes, pipes, lb
Dh/dp = change of enthalpy to change in pressure, Btu/lb psi dT/dp = change of saturation temperature to change in pressure, °F/psi Q = energy transferred to evaporator, Btu/h dp/dz = rate of pressure change, psi/h
Now assuming that the volume of space between the drum level and the valve = V ft3, we can write the following expression for change in pressure using the perfect gas law:
PV = C = pV/m
|
Where |
C = a constant
M = mass of steam, lb, in volume V
Or
PV Cm
-=c or p=—
F =PpV (W, — W,) (86b)
Where
P = pressure, psia Ws, Wi = steam generated and steam withdrawn, lb/h
For steam at 600-630 psia, we have from the steam tables that the saturation temperature = 486°F and 492°F, respectively.
Enthalpy of water = 471.6 and 477.9 Btu/lb Average latent heat hg = 730 Btu/lb Specific volume = 0.75 ft3/lb
Hence
Dh 477.9 — 471.6
■ = 0.21 Btu/lb psi
Dp 30
DT 492 — 486
= 0.2°F/psi
Dp 30
When Q = 0 and Wf = 0, we have from Eq. (86) that
Ws x 730 + (75,000 x 0.12 x 0.2 + 18,000 x 0.21)dp = 0
Dz
Dp 615 x 0.75 .
Dp =—— 115— (Ws — W) = 4 x (Ws — W)
Or, combining this with the previous equation,
Ws x 730 + (5580) x 4 x (Ws — W,) = 0 or Ws = 43,570 lb/h Using Eq. (87),
Dp = 4 x (43,570 — 45,000) = —5720 psi/h or — 1.59 psi/s dz
The pressure decay will be about 1.59 psi/s if this situation continues without correcting feedback such as matching heat input and feedwater flow.
These calculations, though simplistic, give an idea of what happens when, for example, the turbine exhaust gas is switched off. In fresh air fired HRSGs, there is a small time delay, on the order of a minute, before the fresh air fired
burner can come on and fire to full capacity. The steam pressure decay during this period can be evaluated by this procedure.
Q:
Let us assume that the boiler is operating at 45,000 lb/h and suddenly the demand goes to 50,000 lb/h.
Case 1: What happens to the steam pressure if we maintain the same heat
Input to the evaporator and the feedwater supply?
Case 2: What happens if the feedwater is cut off but heat input remains
The same?
A:
Case 1: Q = 45.0 x 106 Btu/h; Wf = 45,000 lb/h; Wl = 50,000 lb/h. First
Let us com-pute the steam generation. Using Eq. (86a), h1 = 471.6 Btu/lb and hf = 189.5 Btu/lb From Eq. (86a),
45,0 x (471.6 — 189.6) + Ws x 730 + 5580 dp = Q
Dz
Also, dp/dz = 4(Ws — 50,000),
Simplifying,
12.69 x 106 + Ws x 730 + 5580 x 4(Ws — 50,000) = 45.9 x 106 Ws = 49,857 lb/h
Thus,
Dp = 4 x (49,857 — 50,000) = -572 psi/h = -0.159 psi/s dz
Case 2: Wf = 0 and Q = 45.9 MM Btu/h. Using the above equations,
Ws x 730 + 5580 x 4(Ws — 50,000) = 45.9 x 106, or Ws = 50,405 lb/h
^ = 1620 psi/h = 0.45 psi/s dz
The pressure actually increases, because the cooling effect of the feedwater is not sensed.
In practice, controls respond fast and restore the balance among heat input, feedwater flow, and steam generation to match the demand. If we cannot adjust the heat input, as in unfired waste heat boilers, the pressure will slide as shown if we withdraw more steam than can be supplied by the boiler.
Q:
Discuss the parameters influencing the test results of an HRSG during performance testing.
A:
The main variables affecting the performance of an HRSG are the gas flow, inlet gas temperature, gas analysis, and steam parameters. Assuming that an HRSG has been designed for a given set of gas conditions, in reality several of the parameters could be different at the time of testing. In the case of a gas turbine HRSG in particular, ambient temperature also influences the exhaust gas conditions. The HRSG could, as a result, be receiving a different gas flow at a different temperature, in which case the steam production would be different from that predicted.
Even if the ambient temperature and the gas turbine load were to remain the same, it is difficult to ensure that the HRSG would receive the design gas flow at the design temperature. This is due to instrument errors. Typically, in large ducts, the gas measurement could be off by 3-5% and the gas temperatures could differ by 10-20°F according to ASME Power Test Code 4.4. As a result it is possible that the HRSG would receive 5% less flow at 10°F lower gas temperature than design conditions, even though the instruments recorded design conditions. As a result, the HRSG steam generation and steam temperature would be less than predicted through no fault of the HRSG design. Figure 8.18 Shows the performance of an HRSG designed for 500,000 lb/h gas flow at 900°F; steam generation is 57,000 lb/h at 650psig and 750°F. The graph shows how the same HRSG behaves when the mass flow changes from 485,000 to 515,000 lb/h while the exhaust temperature varies from 880°F to 902°F. The steam temperature falls to 741°F with 880°F gas temperature, whereas it is 758°F at 920°F. The steam flow increases from 52,900 to 60,900 lb/h as the gas mass flow increases. Thus the figure shows the map of performance of the HRSG for possible instrumental error variations only. Hence HRSG designers and plant users should mutually agree upon possible variations in gas parameters and their influence on HRSG performance before conducting such tests.
8.45b
Q:
Based on operating data, can we determine whether an HRSG is operating well?
FIgure 8.18 HRSG performance as a function of gas flow and temperature.
It is possible to evaluate the operating data for possible deviations from predicted or guaranteed data as shown below. An HRSG supplier has guaranteed certain data for his HRSG in his proposal, which are shown alongside the measured data in Table 8.34. How are these data to be reconciled?
Note that the actual gas flow is difficult to measure and is not shown. However, using an energy balance, one can obtain the gas flow based on energy
|
Table 8.34 Proposed and Actual HRSG Performance
|
Absorbed by steam and the difference between gas temperatures at the inlet and exit. Note that the operating steam pressure is lower than that called for in the design.
From the energy balance, we have Wg x (h, — ho) x 0.99 = Ws Ah
Where h,, ho refer to the enthalpy of gas at the inlet and exit of the HRSG corresponding to the gas temperatures measured. The steam flow, Ws, and the enthalpy absorbed by steam, Ah, are known from steam tables. Hence Wg, the gas flow, can be calculated. It can be shown to be 501,300 lb/h.
Now using the HRSGS program, one can simulate the design mode using the proposal data as shown in Fig. 8.19a. Then, using the calculated gas flow and the inlet temperature, run the HRSGS program in the off-design mode at the lower steam pressure. The results are shown in Fig. 8.19b. It may be seen that 69,520 lb/h of steam should have been generated at 690°F and the exit gas temperature should be 364°F, whereas we measured only 68,700 lb/h and exit gas at 380°F. Hence more analysis is required, but there is a prima facie concern with the HRSG performance.
Estimate the boiling heat transfer coefficient inside tubes for water and the tube wall temperature rise for a given heat flux and steam pressure.
Subcooled boiling heat transfer coefficient inside tubes for water can be estimated by the following equations.
According to Collier [13],
AT = 0.072e-P/1260 q0 5 (87a)
According to Jens and Lottes [13],
AT = 1.9e-P/900 q0 25 (87b)
Where
AT = difference between saturation temperature and tube wall temperature, °F
P = steam pressure, psia q = heat flux inside tubes, Btu/ft2 h
|
|
|
|
|
230 |
Suphtrt wкpl oeoni
Figure 8.19a Simulation of HRSG design data.
|
Suphtrl Evapl Figure 8.19b Simulation of HRSG operating data. |
The heat transfer coefficient is then given by h, = q/AT
What is the boiling heat transfer coefficient inside the tubes, and what is the tube wall temperature if the heat flux inside boiler tubes is 60,000 Btu/ft2 h and steam pressure = 1200 psia?
Solution. Using Collier’s equation,
AT = 0.072 x e-1200/1260 x 60,000°’5 = 6.8°F h, = 60,000/6.8 = 8817 Btu/ft2 h°F
Using Jens and Lottes’s equation,
AT = 1.9 x e-120^900 x 60,000°’25 = 7.8°F h, = 60,000/7.8 = 7650 Btu/ft2 h°F
The above expressions assume that the tube surface where boiling occurs is smooth and clean.
8.47a
Q:
What is the relationship among critical heat flux, steam pressure, quality, and flow in water tube boilers?
A:
Several variables influence the critical heat flux or the departure from nucleate boiling (DNB) condition. These are
Steam pressure
Mass velocity of mixing inside the tubes Steam quality
Tube roughness and cleanliness Tube size and orientation
Correlations such as the Macbeth correlation are available in the literature [13].
The Macbeth correlation is
Qc = 0.00633 x 106 x h/gd-°’1(Gi/106)0 51 x (1 — x) (88a)
Where
Hjg = latent heat of steam, Btu/lb G, = mass velocity inside tubes, lb/ft2 h x = steam quality, expressed as a fraction d, = tube inner diameter, in.
Estimate the critical heat flux under the following conditions:
Steam pressure = 1000 psia Tube inner diameter = 1.5 in.
Mass velocity = 600,000 lb/ft2 h Steam quality = 0.20
Qc = 0.00633 x 106 x 650 x 1.50-01 x 0.60’51 x (1 — 0.2) = 2.43 x 106 Btu/ft2 h
In real-life boilers, the allowable heat flux to avoid DNB is much lower, say 2030% lower, than the values obtained by laboratory tests under controlled conditions due to factors such as roughness of tubes, water quality, and safety considerations. Boiler suppliers have their own data and design boilers accordingly.
8.47b
Q:
How is the critical heat flux qc determined in pool boiling situations as in fire tube boilers?
A:
Several correlations are available in the literature, but only two will be cited. Motsinki suggests the simple equation [13]
(88b)
Where Ps, Pc are the steam pressure and critical pressure, both in psia.
|
|
Where
A = surface tension p = density hg = latent heat
G, g0 = acceleration due to gravity and conversion factor g in force units all in metric units.
Determine the critical heat flux for steam at 400psia under pool boiling conditions.
Solution. The following data can be obtained from steam tables: Saturation temperature at 400psia = 445°F Density of liquid = 51 lb/cu ft (827 kg/m3)
Density of vapor = 0.86lb/cu ft (13.8 kg/m3)
Latent heat of vaporization = 780 Btu/lb (433 kcal/kg)
From Table 8.26 at a saturation temperature of 445°F, surface tension is
0. 0021 lbf/ft (0.31 kgf/m).
G = 9.8 x 36002 m/h2 g0 = 9.8 x 36002 kgm/Kgf h2
Substituting into (88b):
/400 / 400
Qr = 803 x 3208 x ——— x 1—————
Hc V320V V 3208/
= 1.102 MM Btu/ft2 h
Using Eq. (88c),
Qc = 13.8 x 433 x 0.13 x (0.0031 x 813 x 9.82 36004 ’25 Z 827 4 0 5
(13.8)/ V827 + 13.8,
= 2.95 x 106 kcal/m2 = 1.083 MM Btu/ft2 h
Again, As before, factors such as surface roughness, water quality, scale formation, and bundle configuration play a role, and for conservative estimates, boiler designers use a value that is 20-30% of these values.
8.47c
Q:
Estimate the critical heat flux for a tube bundle of a fire tube boiler with the following data:
Tube OD = 2 in.
Number of tubes = 590 Length = 29.5 ft
Tube spacing = 2.75 in., triangular Surface area = 9113 ft2 Tube bundle diameter 78 in.
The heat flux for a tube bundle is obtained by correcting the heat flux for pool boiling obtained from Q8.47b.
First compute a factor C = DbL/A
Where
Db = bundle diameter, ft L = length of tubes, ft A = surface area of bundle, ft2 C = 78 x 29.5 = 0.021 12 x 9113
The correction factor F is obtained from the correlation
Log F = 0.8452 + 0.994 log C
For C = 0.021, logF = -0.8224, or F = 0.15.
Hence,
Corrected heat flux = 1.083 x 106 x 0.15 = 162,500 Btu/ft2 h Typically a value such as 70-80% of this is used for tube bundles.
Discuss the simplified approach to designing fire tube boilers.
Engineers often must estimate the size of heat transfer equipment such as heat exchangers, gas coolers, boilers, and economizers for preliminary costing and to check space requirements. With the approach presented here, one can quickly determine one or more configurations to accomplish a certain amount of heat transfer. One can also size equipment so as to limit the pressure drop without performing lengthy calculations. Life-cycle costing can then be applied to select the optimum design.
Two situations will be discussed [8].
1. The tube-side heat transfer coefficient governs the overall heat transfer. Examples: Fire tube boilers; gas coolers; heat exchangers in which a medium such as air or flue gas flows on the tube side and a fluid with a high heat transfer coefficient flows on the outside. Phase changes can also occur on the outside of the tubes.
2. The shell side governs. Examples: Water tube boilers, steam-air exchangers, and gas-liquid heat transfer equipment. See Q8.49.
In a fire tube boiler, gas flows inside the tubes and a steam-water mixture flows on the outside. The gas heat transfer coefficient is small, about 10-20 Btu/ft2 h °F, compared to the outside coefficient of 2000-3000 Btu/ft2 h °F. The metal resistance is also small; hence the gas-side coefficient governs the overall coefficient and the size of the equipment.
The energy transferred is given by
TOC o "1-5" h z Q = UA AT = WC x (T — T2) (89)
The overall heat transfer coefficient is obtained from Eq. (4),
1 do 1 d do do
— =——————— 1 ln—+ ff — — + ff
U hdi h0 24Km di i di 0
Because the inside coefficient governs U, we can rewrite Eq. (4) as follows (neglecting lower order resistances, such as ho, metal resistance, and fouling factors, which contribute to about 5% of U):
U = 0.95hid (90)
i do
The value of the tube-side coefficient is obtained from the familiar Dittus — Boelter equation, Eq. (8),
Nu = 0.023 Re0 8 Pr0 4
Where
Nu = h^, Re =15.2 f
12k
The fluid transport properties are evaluated at the bulk temperature.
Substituting Eqs. (8)-(11) into Eq. (90) and simplifying, we have the following expression [Eq. (12)]:
H, — = 2.44w°’8F1/d,1’8
Where
TOC o "1-5" h z F = (Cp/m)0’4^’6 (91)
Combining Eqs. (89)-(91) we have, after substituting A = 3.14diLN/12 and for flow per tube w = Wj/N,
‘ = 0.606 x -^DT (92)
AT — W08 d,08
This simple equation relates several important variables. Given Q, AT, W,, and F1, one can try combinations of L, d,, and N to arrive at a suitable configuration. Also, for given thermal data, LN0’2/d0’8 is constant in Eq. (92).
F1 is shown in Table 8.35 For flue gas and air. For other gases, F1 can be computed from Eq. (91).
When a phase change occurs, as in a boiler, AT is written as
TOC o "1-5" h z AT = (T1 ~ ts) ~ (T2 ~ ts) (93)
M(T — ts) — (T2 — ts)] 1 ;
Combining Eqs. (92) and (93) and simplifying, we arrive at the expression
T _ t — L
Ln——— — = 0.606 x —1 x N0’2 x —02 08 (94)
T2 — ts q W02d,08 v ;
Factor — 1/Cp is also given in Table 8.35.
Equation (94) relates the major geometric parameters to thermal performance. Using this method, one need not evaluate heat transfer coefficients.
|
TAble 8.35 Flue Gasa |
Factors Fi/Cp, Fz/Cp, Fz, |
And F3 for |
Air and |
|
|
Temp (°F) |
F1/Cp |
F2 |
F2 = Cp |
F3 |
|
Air |
||||
|
100 |
0.6660 |
0.0897 |
0.3730 |
0.5920 |
|
200 |
0.6870 |
0.0952 |
0.3945 |
0.6146 |
|
300 |
0.7068 |
0.i006 |
0.4140 |
0.6350 |
|
400 |
0.7225 |
0.i056 |
0.4308 |
0.6528 |
|
600 |
0.7446 |
0.1150 |
0.4591 |
0.6810 |
|
1000 |
0.7680 |
0.i220 |
0.4890 |
0.6930 |
|
1200 |
0.7760 |
0.1318 |
0.5030 |
0.7030 |
|
0.1353 |
0.7150 |
|||
|
Flue gasa |
||||
|
200 |
0.6590 |
0.0954 |
0.3698 |
0.5851 |
|
300 |
0.6780 |
0.1015 |
0.3890 |
0.6059 |
|
400 |
0.6920 |
0.1071 |
0.4041 |
0.6208 |
|
600 |
0.7i40 |
0.1170 |
0.4300 |
0.6457 |
|
800 |
0.7300 |
0.1264 |
0.4498 |
0.6632 |
|
1000 |
0.7390 |
0.1340 |
0.4636 |
0.6735 |
|
1200 |
0.7480 |
0.1413 |
0.4773 |
0.6849 |
|
AFlue gas is assumed to have 12% water vapor by volume. |
Now consider gas pressure drop. The equation that relates the geometry to tube — side pressure drop in in. H2O is
2
TOC o "1-5" h z _5 . / V
APi = 9.3 x 10-5 f x I N- (L + 5di) x d5
2 » (95)
= 9.3 x 10-5 x (W) K2V
Where
K2 = f (L + 5di)/df (96)
Combining Eqs. (94)-(96) and eliminating N,
T _ t — v01
Ln——— s = 0.24 x — x K1 —0T (97)
T2 — ts Cp 1 AP®1 v ;
Where
K1 =(L + 5di)°’1Lf°’1/d,1’3 (98)
|
di (in.)
|
|
Table 8.37 Values of K2 as a Function of Tube Diameter and Length Di (in.)
|
K and K2 appear in Tables 8.36 and 8.37 respectively, as a function of tube ID and length. In the turbulent range, the friction factor for cold-drawn tubes is a function of inner diameter.
Using Eq. (97), one can quickly figure the tube diameter and length that limit tube pressure drop to a desired value. Any two of the three variables N, L, and d, determine thermal performance as well as gas pressure drop. Let us discuss the conventional design procedure:
1. Assume w, calculate N.
2. Calculate U, using Eqs. (4) and (90).
3. Calculate L after obtaining A from Eq. (89).
4. Calculate AP, from Eq. (95).
If the geometry or pressure drop obtained is unsuitable, repeat steps 1-4. This procedure is lengthy.
Some examples will illustrate the simplified approach. The preceding equations are valid for single-pass design. However, with minor changes one can derive the relationships for multipass units (e. g., use length = L/2 for two — pass units).
A fire tube waste heat boiler will cool 66,000 lb/h of flue gas from 1160°F to 440°F. Saturation temperature is 350°F. Molecular weight is 28.5, and gas pressure is atmospheric. If L is to be limited to 20 ft due to layout, determine N and AP, for two tube sizes: (1) 2x 1.77 in. (2 in. OD, 1.77 in. ID) and (2) 1.75 x 1.521 in.
Solution. Use Eq. (92) to find N. Use 2 in. tubes. -1/Cp from Table 8.35 is 0.73 for flue gas at the average gas temperature of 0.5 x (1160 + 440) = 800°F.
|
|
20
2.197 = 0.606 x 0.73 xN0 2 x
(66,0) 0’2 x (1.77)0’8
= 0.6089N0’2, N =611
Compute AP, using Eq. (95). From Table 8.37, K2 is 0.035. Compute the gas specific volume.
Density (p) = 28.5 x
V = 32.25 ft3/lb
Substituting into Eq. (95), we have
5 /66,0002
AP, = 9.3 x 10-5 x ( 611 j x 0.035 x 32.25
= 1.23 in. H2O
Repeat the exercise with 1.75 in. tubes; length remains at 20 ft. From Eq. (92) we note that for the same thermal performance and gas flow, N^L/d08 =
a constant. The above concept comes in handy when one wants to quickly figure the effect of geometry on performance. Hence,
02 20 „ 2 20
6110 x———- 08 = N x—————— 0-8
(1. 77)0 . 8 (1. 521)0 ‘ 8
N = 333
With smaller tubes, one needs fewer tubes for the same duty. This is due to a higher heat transfer coefficient; however, the gas pressure drop would be higher. From Table 8.37, K2 =0.076 for 1.521 in. tubes. From Eq. (95),
5 /66,0002
AP, = 9 . 3 x 10 x I ————- x 0.076 x 32.25
333
= 8 . 95 in. H2O
Size the heat exchanger for 2.0 in. tubes with a pressure drop of 3.0 in. H2O. For the same thermal performance, determine the geometry.
So/wft’on. The conventional approach would take several trials to arrive at the right combination. However, with Eq. (97), one can determine the geometry rather easily:
1160 — 350 F, Ky 1
In—————- = 2.197 = 0.24 x — x -^-r-
440 — 350 Cp AP,0 1
FroM Table 8.35, F1/Cp = 0.73; AP, = 3, v= 32.25. Then
1160 — 350 , i
Ln 440 — 350 = 2.197 = 0.24K1 x (32.25)°
X I? = 0.222K1
K1 = 9 . 89
From Table 8.36, we can obtain several combinations of tube diameter and length that have the same K1 value and would yield the same thermal performance and pressure drop. For the 1.77 in. ID tube, L is 21.75 ft. Use Eq. (92) to calculate the number of tubes.
N0 2
2 .197 = 0.606 x 0. 73 x 21.75 x
(66,0) ° . 2 x (1. 77)0. 8 N = 402
Thus, several alternative tube geometries can be arrived at for the same performance, using the preceding approach. One saves a lot of time by not calculating heat transfer coefficients and gas properties.
Such techniques determine the optimum design, given several alternatives. Here, the major operating cost is from moving the gas through the system, and the installed cost is that of the equipment and auxiliaries such as the fan. The lifecycle cost is the sum of the capitalized cost of operation and the installed cost:
LCC = CCo + Ic The capitalized cost of operation is
1 — YT
Cco = Ca Y
1 — Y
Where Y = (1 + e)/(1 + i).
The annual cost of operating the fan is estimated as
Ca = 0.001 x PHCe
|
DPi PZ |
Where the fan power consumption in kW is
P= 1.9 x 10~6 x Wf x
The above procedure is used to evaluate LCC. The alternative with the lowest LCC is usually chosen if the geometry is acceptable. (Ce is cost of electricity.) and H is the number of hours of operation per year.
Discuss the simplified approach to designing water tube boilers.
Whenever gas flows outside a tube bundle—as in water tube boilers, economizers, and heat exchangers with high heat transfer coefficients on the tube side— the overall coefficient is governed by the gas-side resistance. Assuming that the other resistances contribute about 5% to the total, and neglecting the effect of nonluminous transfer coefficients, one may write the expression for U as
U = 0.95ho (99a)
Where the outside coefficient, ho, is obtained from
Nu = 0.35 Re06 Pr0 3 (99b)
XT hOdO r, Gd T>
Nu = -^7-, Re = ^j— , Pr =
12k 12 m k
|
G = 12 |
O
NwL(Sr — d0)
Equation (99) is valid for both in-line (square or rectangular pitch) and staggered (triangular pitch) arrangements. For bare tubes, the difference in h0 between inline and staggered arrangements at Reynolds numbers and pitches found in practice is 3-5%. For finned tubes, the variation is significant.
Substituting Eqs. (17)-(21 ) into Eq. (99a) and (99b) and simplifying,
TOC o "1-5" h z h0 = 0 . 945 G0. 6F2/d00 ‘ 4 (100)
U = 0 . 9G0 ‘6F2/d°’4 (101)
Where
F = k0 7(cp/m)0 3 (102)
F2 is given in Table 8.35. Gas transport properties are computed at the film temperature.
A = pd-NwNdL/12
Combining the above with Eq. (89) and simplifying gives
G/AT = UA = p0 . 9G0 . 6F2d0NwNdL/12d — A
= 0.235 FG0 . 6NwNdLd — .6
|
Q № -4l° -4n Q =1. °36F2W° •6 N L Nd° 6 AT 2 o (ST=do — I)06 |
Substituting for G from Eq. (21),
-Q = 1 .°36F2W°• 6 ^-6 (1°3)
The above equation relates thermal performance to geometry. When there is a phase change, as in a boiler, further simplification leads to
*■ Ј-=2 ^1x (104)
If the tube diameter and pitch are known, one can estimate Nd or G for a desired
Thermal performance.
Let us now account for gas pressure drop. The equation that relates the gas
Pressure drop to G is Eq. (28) of Chapter 7:
APo = 9 . 3 x 10-10 x G2f — o P
For in-line arrangements, the friction factor is obtained from Eq. (29) of Chapter 7:
-0.15
F = Re
Where
0.08SL/dO
X = 0.044+ —
(ST/do — 1)°-43+1’13do/SL Another form of Eq. (28) of Chapter 7 is
|
VNj^V^x |
A1.85
|
(105) |
APo = 1.34 x 10“
N1-85L1’85do°’15(ST — do)1
Substituting for f in Eq. (28) of Chapter 7 and combining with Eq. (104) we can relate DPo to performance in a single equation:
DPo = 4.78 x 10-1° x G2 25 (ST — do)
~ ~ X
T1 —
|
X ln |
(106)
DO 75 F3P
Where
|
0 15 |
|
(107) |
F3 = (F2/C>
F3 is given in Table 8.35. With Eq. (107), one can easily calculate the geometry for a given tube bank so as to limit the pressure drop to a desired value. An example will illustrate the versatility of the technique.
In a water tube boiler, 66,000 lb/h of flue gas is cooled from 1160°F to 440°F. Saturation temperature is 350°F. Tube outside diameter is 2 in., and an in-line arrangement is used with ST = SL = 4 in. Determine a suitable configuration to limit the gas pressure to 3 in. H2O.
Let us use Eq. (106). Film temperature is 0.5 x (800 + 350) = 575°F. Interpolating from Table 8.35 at 475°F, F3 = 0 . 643. Gas density at 800°F is 0.031 lb/ft3 from Example 1. 3
DPo = 4 . 78 x 10-1° x G2 25 (4 — 2)
, T1160 — 3501 x ln
440 — 350 (0.044 + 0.08 x 2)
X 20•75 x 0 . 643 x 0 .031 = 128 x 10-10 x G2 25 = 3
Hence, G = 5200lb/ft2 h. From Eq. (21) one can choose different combinations of Nw and L:
NwL = 66,000 x 12/(2 x 5200) = 76
If Nw = 8, then L = 9.5 ft.
Calculate Nd from Eq. (104):
|
In |
|
= 2 .197 |
116° — 350
44° — 350
Cp G0-4(Srd0 -1)d0 4
2 .197 = 2.82 x 0.426Nd/(5200a4 x 1 x 20 4) or Nd = 74 Thus, the entire geometry has been arrived at.
How is the bundle diameter of heat exchangers or fire tube boilers determined? A:
Tubes of heat exchangers and fire tube boilers are typically arranged in square or triangular pitch (Fig. 8.20). The ratio of tube pitch to diameter could range from 1.25 to 2 depending on the tube size and the manufacturer’s past practice.
Looking at the triangular pitch arrangement, we see that haf of a tube area is located within the triangle, whose area is given by
Area of triangle = 0.5 x 0.866p2 = 0 .433_p2
If there are N tubes in the bundle, then
Total area occupied = 0.866Np2
If the bundle diameter is D, then 3 .14 x D2/4 = area of bundle = 0.866Np2, or
D = 1. 05^№ 5 (108)
Similarly, for the square pitch, the area occupied by one tube = ^2. Hence bundle area = 3.14 x D2/4 = N^2, or
D = 1.128^№ • 5 (109)
In practice, a small clearance is added to the above number for manufacturing purposes.
|
FIgure 8.20 Square (top) and triangular (bottom) pitch for boiler/exchanger tubes. |
If 500 tubes of 2 in. diameter are located in a fire tube boiler shell at a triangular pitch of 3 in., the bundle diameter would be
D = 1.05 x 3 x 500° • 5 = 70 . 5 in.
If the pitch were square, the bundle diameter would be
D = 1.128 x 3 x 500° . 5 = 75 .7 in.
Sometimes tubes have to be located within a given sector of a circle. In such cases, it is helpful to know the area of a sector of a circle gIven its height and diameter. Table 8.38 gives the factor C, which when multiplied by D2 gives the sector area.
Find the area of a sector of height 10 in. and diameter 24 in.
Solution. For h/D = 10/24 = 0.4167, C from Table 8.38 = 0.309. Hence, Area = C x D2 = 0. 309 x 24 x 24 = 178 in. 2
8.51
Q:
How is the thickness of insulation for a flat or curved surface determined? Determine the thickness of insulation to limit the casing surface temperature of a pipe operating from 800°F to 200°F, when
Ambient temperature ta = 80°F
Thermal conductivity of insulation Km at average temperature of 500°F = 0.35 Btu in./ft2 h °F Pipe outer diameter d = 12 in.
Wind velocity V = 264 ft/min (3 mph)
Emissivity of casing = 0.15 (oxidized)
|
H/D |
C |
H/D |
C |
H/D |
C |
H/D |
C |
H/D |
C |
|
0.050 |
0.01468 |
0.100 |
0.04087 |
0.150 |
0.07387 |
0.200 |
0.11182 |
||
|
0.001 |
0.00004 |
0.051 |
0.01512 |
0.101 |
0.04148 |
0.151 |
0.07459 |
0.201 |
0.11262 |
|
0.002 |
0.00012 |
0.052 |
0.01556 |
0.102 |
0.04208 |
0.152 |
0.07531 |
0.202 |
0.11343 |
|
0.003 |
0.00022 |
0.053 |
0.01601 |
0.103 |
0.04269 |
0.153 |
0.07603 |
0.203 |
0.11423 |
|
0.004 |
0.00034 |
0.054 |
0.01646 |
0.104 |
0.04330 |
0.154 |
0.07675 |
0.204 |
0.11504 |
|
0.005 |
0.00047 |
0.055 |
0.01691 |
0.105 |
0.04391 |
0.155 |
0.07747 |
0.205 |
0.11584 |
|
0.006 |
0.00062 |
0.056 |
0.01737 |
0.106 |
0.04452 |
0.156 |
0.07819 |
0.206 |
0.11665 |
|
0.007 |
0.00078 |
0.057 |
0.01783 |
0.107 |
0.04514 |
0.157 |
0.07892 |
0.207 |
0.11746 |
|
0.008 |
0.00095 |
0.058 |
0.01830 |
0.108 |
0.04578 |
0.158 |
0.07965 |
0.208 |
0.11827 |
|
0.009 |
0.00113 |
0.059 |
0.01877 |
0.109 |
0.04638 |
0.159 |
0.08038 |
0.209 |
0.11908 |
|
0.010 |
0.00133 |
0.060 |
0.01924 |
0.110 |
0.04701 |
0.160 |
0.08111 |
0.210 |
0.11990 |
|
0.011 |
0.00153 |
0.061 |
0.01972 |
0.111 |
0.04763 |
0.161 |
0.08185 |
0.211 |
0.12071 |
|
0.012 |
0.00175 |
0.062 |
0.02020 |
0.112 |
0.04826 |
0.162 |
0.08258 |
0.212 |
0.12153 |
|
0.013 |
0.00197 |
0.063 |
0.02068 |
0.113 |
0.04889 |
0.163 |
0.08332 |
0.213 |
0.12235 |
|
0.014 |
0.00220 |
0.064 |
0.02117 |
0.114 |
0.04953 |
0.164 |
0.08406 |
0.214 |
0.12317 |
|
0.015 |
0.00244 |
0.065 |
0.02166 |
0.115 |
0.05016 |
0.165 |
0.08480 |
0.215 |
0.02399 |
|
0.016 |
0.00268 |
0.066 |
0.02215 |
0.116 |
0.05080 |
0.166 |
0.08554 |
0.216 |
0.12481 |
|
0.017 |
0.00294 |
0.067 |
0.02265 |
0.117 |
0.05145 |
0.167 |
0.08629 |
0.217 |
0.12563 |
|
0.018 |
0.00320 |
0.068 |
0.02315 |
0.118 |
0.05209 |
0.168 |
0.08704 |
0.218 |
0.12646 |
|
0.019 |
0.00347 |
0.069 |
0.02366 |
0.119 |
0.05274 |
0.169 |
0.08779 |
0.219 |
0.12729 |
|
0.020 |
0.00375 |
0.070 |
0.02417 |
0.120 |
0.05338 |
0.170 |
0.08854 |
0.220 |
0.12811 |
|
0.021 |
0.00403 |
0.071 |
0.02468 |
0.121 |
0.05404 |
0.171 |
0.08929 |
0.221 |
0.12894 |
|
0.022 |
0.00432 |
0.072 |
0.02520 |
0.122 |
0.05469 |
0.172 |
0.09004 |
0.222 |
0.12977 |
|
0.023 |
0.00462 |
0.073 |
0.02571 |
0.123 |
0.05535 |
0.173 |
0.09080 |
0.223 |
0.13060 |
|
0.024 |
0.00492 |
0.074 |
0.02624 |
0.124 |
0.05600 |
0.174 |
0.09155 |
0.224 |
0.13144 (continued ) |
H/D C h/D C h/D
|
0.025 |
0.00523 |
0 |
|
0.026 |
0.00555 |
0 |
|
0.027 |
0.00587 |
0 |
|
0.028 |
0.00619 |
0 |
|
0.029 |
0.00653 |
0 |
|
0.030 |
0.00687 |
0 |
|
0.031 |
0.00721 |
0 |
|
0.032 |
0.00756 |
0 |
|
0.033 |
0.00791 |
0 |
|
0.034 |
0.00827 |
0 |
|
0.035 |
0.00864 |
0 |
|
0.036 |
0.00901 |
0 |
|
0.037 |
0.00938 |
0 |
|
0.038 |
0.00976 |
0 |
|
0.039 |
0.01015 |
0 |
|
0.040 |
0.01054 |
0 |
|
0.041 |
0.01093 |
0 |
|
0.042 |
0.01133 |
0 |
|
0.043 |
0.01173 |
0 |
|
0.044 |
0.01214 |
0 |
|
0.045 |
0.01255 |
0 |
|
0.046 |
0.01297 |
0 |
|
0.047 |
0.01339 |
0 |
|
0.048 |
0.01382 |
0 |
|
0.049 |
0.01425 |
0 |
|
0.250 |
0.15355 |
0 |
|
.075 |
0.02676 |
0.125 |
|
.076 |
0.02729 |
0.126 |
|
.077 |
0.02782 |
0.127 |
|
.078 |
0.02836 |
0.128 |
|
.079 |
0.02889 |
0.129 |
|
.080 |
0.02943 |
0.130 |
|
.081 |
0.02998 |
0.131 |
|
.082 |
0.03053 |
0.132 |
|
.083 |
0.03108 |
0.133 |
|
.084 |
0.03163 |
0.134 |
|
.085 |
0.03219 |
0.135 |
|
.086 |
0.03275 |
0.136 |
|
.087 |
0.03331 |
0.137 |
|
.088 |
0.03387 |
0.138 |
|
.089 |
0.03444 |
0.139 |
|
.090 |
0.03501 |
0.140 |
|
.091 |
0.03559 |
0.141 |
|
.092 |
0.03616 |
0.142 |
|
.093 |
0.03674 |
0.143 |
|
.094 |
0.03732 |
0.144 |
|
.095 |
0.03791 |
0.145 |
|
.096 |
0.03850 |
0.146 |
|
.097 |
0.03909 |
0.147 |
|
.098 |
0.03968 |
0.148 |
|
.099 |
0.04028 |
0.149 |
|
.300 |
0.19817 |
0.350 |
|
С h/D С h/D С
|
|
0.251 |
0.15441 |
0 |
|
0.252 |
0.15528 |
0 |
|
0.253 |
0.15615 |
0 |
|
0.254 |
0.15702 |
0 |
|
0.255 |
0.15789 |
0 |
|
0.256 |
0.15876 |
0 |
|
0.257 |
0.15964 |
0 |
|
0.258 |
0.16501 |
0 |
|
0.259 |
0.16139 |
0 |
|
0.260 |
0.16226 |
0 |
|
0.261 |
0.16314 |
0 |
|
0.262 |
0.16402 |
0 |
|
0.263 |
0.16490 |
0 |
|
0.264 |
0.16578 |
0 |
|
0.265 |
0.16666 |
0 |
|
0.266 |
0.16755 |
0 |
|
0.267 |
0.16843 |
0 |
|
0.268 |
0.16932 |
0 |
|
0.269 |
0.17020 |
0 |
|
0.270 |
0.17109 |
0 |
|
0.271 |
0.17198 |
0 |
|
0.272 |
0.17287 |
0 |
|
0.273 |
0.17376 |
0 |
|
0.274 |
0.17465 |
0 |
|
0.275 |
0.17554 |
0 |
|
0.276 |
0.17644 |
0 |
|
0.277 |
0.17733 |
0 |
|
0.278 |
0.17823 |
0 |
|
301 |
0.19908 |
0.351 |
|
302 |
0.20000 |
0.352 |
|
303 |
0.20092 |
0.353 |
|
304 |
0.20184 |
0.354 |
|
305 |
0.20276 |
0.355 |
|
306 |
0.20368 |
0.356 |
|
307 |
0.20460 |
0.357 |
|
308 |
0.20553 |
0.358 |
|
309 |
0.20645 |
0.359 |
|
310 |
0.20738 |
0.360 |
|
311 |
0.20830 |
0.361 |
|
312 |
0.20923 |
0.362 |
|
313 |
0.21015 |
0.363 |
|
314 |
0.21108 |
0.364 |
|
315 |
0.21201 |
0.365 |
|
316 |
0.21294 |
0.366 |
|
317 |
0.21387 |
0.367 |
|
318 |
0.21480 |
0.368 |
|
319 |
0.21573 |
0.369 |
|
320 |
0.21667 |
0.370 |
|
321 |
0.21760 |
0.371 |
|
322 |
0.21853 |
0.372 |
|
323 |
0.21947 |
0.373 |
|
324 |
0.22040 |
0.374 |
|
325 |
0.22134 |
0.375 |
|
326 |
0.22228 |
0.376 |
|
327 |
0.22322 |
0.377 |
|
328 |
0.22415 |
0.378 |
|
0.24593 |
0.401 |
0.29435 |
0.451 |
0.34378 |
|
0.24689 |
0.402 |
0.29533 |
0.452 |
0.34477 |
|
0.24784 |
0.403 |
0.29631 |
0.453 |
0.34577 |
|
0.24880 |
0.404 |
0.29729 |
0.454 |
0.34676 |
|
0.24976 |
0.405 |
0.29827 |
0.455 |
0.34776 |
|
0.25071 |
0.406 |
0.29926 |
0.456 |
0.34876 |
|
0.25167 |
0.407 |
0.30024 |
0.457 |
0.34975 |
|
0.25263 |
0.408 |
0.30122 |
0.458 |
0.35075 |
|
0.25359 |
0.409 |
0.30220 |
0.459 |
0.35175 |
|
0.25455 |
0.410 |
0.30319 |
0.460 |
0.35274 |
|
0.25551 |
0.411 |
0.30417 |
0.461 |
0.35374 |
|
0.25647 |
0.412 |
0.30516 |
0.462 |
0.35474 |
|
0.25743 |
0.413 |
0.30614 |
0.463 |
0.35573 |
|
0.25839 |
0.414 |
0.30712 |
0.464 |
0.35673 |
|
0.25936 |
0.415 |
0.30811 |
0.465 |
0.35773 |
|
0.26032 |
0.416 |
0.30910 |
0.466 |
0.35873 |
|
0.26128 |
0.417 |
0.31008 |
0.467 |
0.35972 |
|
0.26225 |
0.418 |
0.31107 |
0.468 |
0.36072 |
|
0.26321 |
0.419 |
0.31205 |
0.469 |
0.36172 |
|
0.26418 |
0.420 |
0.31304 |
0.470 |
0.36272 |
|
0.26514 |
0.421 |
0.31403 |
0.471 |
0.36372 |
|
0.26611 |
0.422 |
0.31502 |
0.472 |
0.36471 |
|
0.26708 |
0.423 |
0.31600 |
0.473 |
0.36571 |
|
0.26805 |
0.424 |
0.31699 |
0.474 |
0.36671 |
|
0.26901 |
0.425 |
0.31798 |
0.475 |
0.36771 |
|
0.26998 |
0.426 |
0.31897 |
0.476 |
0.36871 |
|
0.27095 |
0.427 |
0.31996 |
0.477 |
0.36971 |
|
0.27192 |
0.428 |
0.32095 |
0.478 |
0.37071 (continued) |
|
H/D |
C |
H/D |
C |
H/D |
C |
H/D |
C |
H/D |
C |
|
0.279 |
0.17912 |
0.329 |
0.22509 |
0.379 |
0.27289 |
0.429 |
0.32194 |
0.479 |
0.37171 |
|
0.280 |
0.18002 |
0.330 |
0.22603 |
0.380 |
0.27386 |
0.430 |
0.32293 |
0.480 |
0.37270 |
|
0.281 |
0.18092 |
0.331 |
0.22697 |
0.381 |
0.27483 |
0.431 |
0.32392 |
0.481 |
0.37370 |
|
0.282 |
0.18182 |
0.332 |
0.22792 |
0.382 |
0.27580 |
0.432 |
0.32491 |
0.482 |
0.37470 |
|
0.283 |
0.18272 |
0.333 |
0.22886 |
0.383 |
0.27678 |
0.433 |
0.32590 |
0.483 |
0.37570 |
|
0.284 |
0.18362 |
0.334 |
0.22980 |
0.384 |
0.27775 |
0.434 |
0.32689 |
0.484 |
0.37670 |
|
0.285 |
0.18452 |
0.335 |
0.23074 |
0.385 |
0.27872 |
0.435 |
0.32788 |
0.485 |
0.37770 |
|
0.286 |
0.18542 |
0.336 |
0.23169 |
0.386 |
0.27969 |
0.436 |
0.32887 |
0.486 |
0.37870 |
|
0.287 |
0.18633 |
0.337 |
0.23263 |
0.387 |
0.28067 |
0.437 |
0.32987 |
0.487 |
0.37970 |
|
0.288 |
0.18723 |
0.338 |
0.23358 |
0.388 |
0.28164 |
0.438 |
0.33086 |
0.488 |
0.38070 |
|
0.289 |
0.18814 |
0.339 |
0.23453 |
0.389 |
0.28262 |
0.439 |
0.33185 |
0.489 |
0.38170 |
|
0.290 |
0.18905 |
0.340 |
0.23547 |
0.390 |
0.28359 |
0.440 |
0.33284 |
0.490 |
0.38270 |
|
0.291 |
0.18996 |
0.341 |
0.23642 |
0.391 |
0.28457 |
0.441 |
0.33384 |
0.491 |
0.38370 |
|
0.292 |
0.19086 |
0.342 |
0.23737 |
0.392 |
0.28554 |
0.442 |
0.33483 |
0.492 |
0.38470 |
|
0.293 |
0.19177 |
0.343 |
0.23832 |
0.393 |
0.28652 |
0.443 |
0.33582 |
0.493 |
0.38570 |
|
0.294 |
0.19268 |
0.344 |
0.23927 |
0.394 |
0.28750 |
0.444 |
0.33682 |
0.494 |
0.38670 |
|
0.295 |
0.19360 |
0.345 |
0.24022 |
0.395 |
0.28848 |
0.445 |
0.33781 |
0.495 |
0.38770 |
|
0.296 |
0.19451 |
0.346 |
0.24117 |
0.396 |
0.28945 |
0.446 |
0.33880 |
0.496 |
0.38870 |
|
0.297 |
0.19542 |
0.347 |
0.24212 |
0.397 |
0.29043 |
0.447 |
0.33980 |
0.497 |
0.38970 |
|
0.298 |
0.19634 |
0.348 |
0.24307 |
0.398 |
0.29141 |
0.448 |
0.34079 |
0.498 |
0.39070 |
|
0.299 |
0.19725 |
0.349 |
0.24403 |
0.399 |
0.29239 |
0.449 |
0.34179 |
0.499 0.500 |
0.38170 0.39270 |
The heat loss q from the surface is given by [7]
|
Ta + 459.6 100 + 68.9 68.9 J |
|
Q = 0.174s |
|
1/2 |
|
125 (v + 0.296 (ts — ta)125 x |
|
Ts + 459.6 100 |
 |
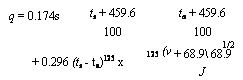E may be taken as 0.9 for oxidized steel, 0.05 for polished aluminum, and 0.15 for oxidized aluminum. Also,
|
= 0.74 in. |
|
Le = 0.35 x ■ |
|
285 We can solve for L given Le and d by using Eq. (112) and trial and error, or we can use Table 8.39. It can be shown that L = 0.75 in. The next standard thickness available will be chosen. A trial-and-error method as discussed next will be needed to solve for the surface temperature ts. (Note that L is the actual thickness of insulation.) |
|
D + 2L, d + 2L Le = —-— ln |
|
(112) |
|
2 d Substituting ts = 200, ta = 80, V = 264, and e = 0.15 into Eq. (110), we have q = 0.173 x 0.15 x (6.64 — 5.44) + 0.296 X (660 — 540)125 x = 285 Btu/ft2 h From Eq. (111), 800 — 200 |
|
0.5 |
|
1.25 /264 + 69 |
|
69 |
|
Km(t — ts) |
|
Km(t — ts) ‘ Le |
|
Q = |
|
[(d + 2L)/2] x ln[(d + 2L)/d] |
 |
|
|
|
|
|
|
 |
|
 |
|
|
|
Tube diam. d (in.) |
Thickness of insulation L (in.; |
1 |
||||||
|
0.5 |
1 |
1.5 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
|
|
1 |
0.69 |
1.65 |
2.77 |
4.0 |
6.80 |
9.90 |
13.2 |
16.7 |
|
2 |
0.61 |
1.39 |
2.29 |
3.30 |
5.50 |
8.05 |
10.75 |
13.62 |
|
3 |
0.57 |
1.28 |
2.08 |
2.97 |
4.94 |
7.15 |
9.53 |
12.07 |
|
4 |
0.56 |
1.22 |
1.96 |
2.77 |
4.55 |
6.60 |
8.76 |
11.10 |
|
5 |
0.55 |
1.18 |
1.88 |
2.65 |
4.34 |
6.21 |
8.24 |
10.40 |
|
6 |
0.54 |
1.15 |
1.82 |
2.55 |
4.16 |
5.93 |
7.85 |
9.80 |
|
8 |
0.53 |
1.12 |
1.75 |
2.43 |
3.92 |
5.55 |
7.50 |
9.15 |
|
10 |
0.52 |
1.09 |
1.70 |
2.35 |
3.76 |
5.29 |
6.93 |
8.57 |
|
12 |
0.52 |
1.08 |
1.67 |
2.30 |
3.65 |
5.11 |
6.65 |
8.31 |
|
16 |
0.52 |
1.06 |
1.63 |
2.23 |
3.50 |
4.86 |
6.31 |
7.83 |
|
20 |
0.51 |
1.05 |
1.61 |
2.19 |
3.41 |
4.70 |
6.10 |
7.52 |
|
ALe = d ln d ~d2L■ For example, for d = 3 and L = 1.5, Le = 2.08. |
Calculate the equivalent thickness Le. From Eq. (112),
12 + 2 14
Le = —2— Y2 = 108 m-
Assume that for the first trial ts = 150°F. Let Km at a mean temperature of (800 + 150)/2 = 475°F be 0.34 Btuin./ft2h °F. From Eq. (110),
Q = 0.173 x 0.15 x (6.14 — 5.44) + 0.296 x(610 — 540)125 X = 145 Btu/ft2 h
From Eq. (111),
800 — 150 2
Q = 0. 34 x ———— = 205 Btu/ft h 1 08
Because these two values of q do not agree, we must go for another trial. Try ts = 170°F. Then, from Eq. (110),
Q = 200 Btu/ft2 h
And from Eq. (111), q = 198 Btu/ft2 h
These two are quite close. Hence the final surface temperature is 170°F, and the heat loss is about 200 Btu/ft2 h.
8.53 Q:
A horizontal flat surface is at 10°F. The ambient dry bulb temperature is 80°F, and the relative humidity is 80%. Determine the thickness of fibrous insulation that will prevent condensation of water vapor on the surface. Use Km = 0.28Btu/fth°F. The wind velocity is zero. Use a surface emissivity of 0.9 for the casing.
The surface temperature must be above the dew point of water to prevent condensation of water vapor. Q5.10 shows how the dew point can be calculated. The saturated vapor pressure at 80°F, from the steam tables in the Appendix, is 0.51 psia. At 80% relative humidity, the vapor pressure will be 0.8 x 0.51 = 0.408 psia. From the steam tables, this corresponds to a saturation temperature of 73°F, which is also the dew point. Hence we must design the insulation so the casing temperature is above 73°F.
From Eq. (110),
Q = 0 .173 x 0 . 9 x (5 . 44 — 5 . 334)
+ 0.296 x (80 — 73)1 25 = 10 .1 Btu/ft2 h
Also, from Eq. (111),
K 0 28
Q = (d — ts)xKmm = (73 — 10)x —
(In this case of a flat surface, Le = L.)
Note that the heat flow is from the atmosphere to the surface. td and ts are the dew point and surface temperature, °F. Solving for L, we get L = 1.75 in.
Hence, by using the next standard insulation thickness available, we can
Ensure that the casing is above the dew point. To obtain the exact casing
Temperature with the standard thickness of insulation, a trial-and-error procedure as discussed in Q8.52 may be used. But this is not really necessary, because we have provided a safe design thickness.
A 11 in. schedule 40 pipe 1000 ft long carries hot water at 300°F. What is the heat loss from its surface if it is not insulated (case 1) or if it has 1 in., 2 in., and 3 in. thick insulation (case 2)?
The thermal conductivity of insulation may be assumed to be 0.25 Btuin./ft2 h°F. The ambient temperature is 80°F, and the wind velocity is zero.
Case 1. Equation (110) can be used to determine the heat loss. For the bare pipe surface, assume that e is 0.90. Then
Q = 0.173 x 0.9 x (7.64 — 5.44)
+ 0.296 x (300 — 80)1,25 = 638 Btu/ft2 h
Case 2. Determination of the surface temperature given the insulation thickness involves a trial-and-error procedure as discussed in Q8.52 and will be done in detail for the 1 in. case.
Various surface temperatures are assumed, and q is computed from Eqs.
(110) and (111). Let us use a e value of 0.15. The following table gives the results
Of the calculations.
|
Ts |
Q from Eq. (110) |
Q from Eq. (111) |
|
110 |
26 |
34 |
|
120 |
37 |
32 |
|
140 |
61 |
28 |
We can draw a graph of ts versus q with these values and obtain the correct ts. However, we see from the table, by interpolation, that at ts = 115°F, q, from both equations, is about 33 Btu/ft2 h.
3.9
Total heat loss = 3.14 x — x 1000 x 33 12
= 33,675 Btu/h
Similarly, we may solve for q when the thicknesses are 2 and 3 in. It can be shown that at L = 2 in., q = 15 Btu/ft2 h, and at L = 3 in., q = 9 Btu/ft2 h. Also, when L = 2in., ts = 98°F and total heat loss = 23,157 Btu/h. When L = 3in., ts = 92°F and total loss = 18,604 Btu/h. s
Estimate the drop in water temperature of 1 in. thick insulation used in Q8.54a. The water flow is 7500 lb/h.
The total heat loss has been shown to be 33,675 Btu/h. This is lost by the water and can be written as 7500 AT, where AT is the drop in temperature, assuming that the specific heat is 1. Hence
33,675
AT = ——- = 4.5°F
7500
By equating the heat loss from insulation to the heat lost by the fluid, be it air, oil, steam, or water, one can compute the drop in temperature in the pipe or duct. This calculation is particularly important when oil lines are involved, because viscosity is affected, leading to pumping and atomization problems.
8.55
In Q8.54 determine the optimum thickness of insulation with the following data.
Cost of energy = $3/MM Btu
Cost of operation = $8000/year
Interest and escalation rates = 12% and 7%
Life of the plant = 15 years
Total cost of 1 in. thick insulation, including labor and material, = $5200; for 2in. insulation, $7100; and for 3in. insulation, $10,500
Let us calculate the capitalization factor F from Q5.22.
F = 107 x 1 -(1.°7/1.12)15 = 10.5
1.12 1 — 1.07/1.12
Let us calculate the annual heat loss.
For L = 1 in.,
8000
Ca = 33,675 x 3 x =
8000
Ca = 23,157 x 3 x -0^- = $555 For L = 3in.,
8000
Ca = 18,604 x 3 x = $446
Calculate capitalized cost CaF.
For L = 1 in.,
CaF = 808 x 10.5 = $8484
For L = 2in.,
CaF = 555 x 10 . 5 = $5827
For L = 3in.,
CaF = 446 x 10.5 = $4683
Calculate total capitalized cost or life-cycle cost (LCC):
For L = 1 in.,
LCC = 8484 + 5200 = $13,684
For L = 2 in., LCC = $12,927; and for L = 3in., LCC = $15,183.
Hence we see that the optimum thickness is about 2 in. With higher thicknesses, the capital cost becomes more than the benefits from savings in heat loss. A trade-off would be to go for 2 in. thick insulation.
Several factors enter into calculations of this type. If the period of operation were less, probably a lesser thickness would be adequate. If the cost of energy were more, we might have to go for a greater thickness. Thus each case must be evaluated before we decide on the optimum thickness. This example gives only a methodology, and the evaluation can be as detailed as desired by the plant engineering personnel.
If there were no insulation, the annual heat loss would be
1.9 8000
3 .14 x — x 1000 x 638 x 3 x —- = $7600 12 106
Hence simple payback with even 1 in. thick insulation is 5200/ (7600 — 808) = 0.76 year, or 9 months.
What is a hot casing? What are its uses?
Whenever hot gases are contained in an internally refractory-lined (or insulated) duct, the casing temperature can fall below the dew point of acid gases, which can seep through the refractory cracks and cause acid condensation, which is a potential problem. To avoid this, some engineers prefer a ‘‘hot casing’’ design, which ensures that the casing or the vessel or duct containing the gases is maintained at a high enough temperature to minimize or prevent acid condensation. At the same time, the casing is also externally insulated to minimize the heat losses to the ambient (see Fig. 8.21). A ‘‘hot casing’’ is a combination of internal plus external insulation used to maintain the casing at a high enough temperature to avoid acid condensation while ensuring that the heat losses to the atmosphere are low.
Consider the use of a combination of two refractories inside the boiler casing: 4in. of KS4 and 2 in. of CBM. The hot gases are at 1000°F. Ambient temperature = 60°F, and wind velocity is 100ft/min. Casing emissivity is 0.9. To keep the boiler casing hot, an external 0.5 in. of mineral fiber is added. Determine the boiler casing temperature, the outer casing temperature, and the heat loss.
One can perform the calculations discussed earlier to arrive at the temperatures and heat loss. For the sake of illustrating the point, a computer printout of the result is shown in Fig. 8.22. It can be seen that the boiler casing is at 392°F, and the outermost casing is at 142°F. The heat loss is 180 Btu/ft2h. The boiler casing is hot enough to avoid acid condensation, while the heat losses are kept low.
|
|
|
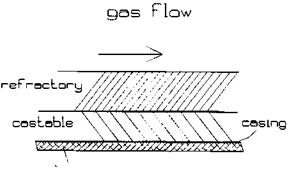
Project: HOT CASING
|
COND1 TEMP2 COND2 |
THICK-IN TEMP-F TКMP1
|
0.00 0.^5 0.72 6. 20 |
Casing
Deltbd/nif ft ib
Cbm
KsM
0.00 142.27 0.00
0.50 392.02 200.00
2.00 800.12 200.00
4.00 1001.42 800.00
0. 00 0.00 0.32 400.00
0.57 600.00
6.02 1600.00
HEAT LOSS — BTU/ft2h — 179 5997 Number of layers of insulation — 3 AMB TEMP« 70 WIND VEL-fpm — 100 EMISS — .9 MAX LOSS-BTU/FT2H» 9330.736
Figure 8.22 Printout on casing temperatures.
What happens if ducts or stacks handling flue gases are not insulated? What would the gas or stack wall temperature be?
This question faces engineers involved in engineering of boiler plants. If ducts and stacks are not insulated, the heat loss from the casing can be substantial. Also, the stack wall temperature can drop low enough to cause acid dew point corrosion.
|
Q = 0.174s x |
|
The temperature drop across the gas film is given by |
Let the flue gas flow be W lb/h at a temperature of tg1 at the inlet to the duct or stack (Fig. 8.23). The heat loss from the casing wall is given by Eq. (110),
|
|
Hc = convective heat transfer coefficient Btu/ft2 h °F do, d,- = outer and inner diameter of the stack, in.
W 0,8C
Hc = 2:44 x d1-8
Where, from Eq. (12),
|
|
The duct wall temperature drop is given by Eq. (111), which can be rearranged to give
|
|
Where tw1, two are the inner and outer wall temperatures, °F.
The total heat loss from the duct or stack is Q = 3. 14do x H/12 where H is the height, ft. The exit gas temperature is then
|
|
T-Tg.2-Twi.3-Two.4-Tc.5-To
Figure 8.23 Stack wall temperature.
The above equations have to be solved iteratively. A trial value for tg2 is assumed, and the gas properties are computed at the average gas temperature. The casing temperature is also obtained through an iterative process. The total heat loss is computed and tg2 is again evaluated. If the assumed and calculated tg2 values agree, then iteration stops. A computer program can be developed to obtain accurate results, particularly if the stack is tall and calculations are better done in several segments.
110,0 lb/h of flue gases at 410°F enter a 48 in. ID stack that is 50 ft long and 1 in. thick. If the ambient temperature is 70° F and wind velocity is 125 ft/min, determine the casing temperature, total heat loss, and exit gas temperature.
Flue gas properties can be assumed to be as follows at 400°F (or computed from methods discussed in Q8.12 if analysis is known): Cp = 0.265, m = 0.058 lb/fth, k = 0.0211 Btu/fth °F. Let the gas temperature drop in the stack = 20°F; hence the exit gas temperature = 390°F.
The gas-side heat transfer coefficient is
|
0.4 0.058) |
0
2.44 x (110,000)°’8 x (———- ) x (0.0211)0’6 = 4.5 Btu/ft2 h °F
Let the casing temperature tc (= two without insulation) be 250°F. q = 0.174 x 0.9 x [(7.1)4 — (5.3)4]
+ 0.296 x (710 — 530)1’25 x ^125 + 69^
69
= 601 Btu/ft2 h
Gas temperature drop across gas film = 601/4.5 = 134°F.
Temperature drop across the stack wall =
601 x 50 x ^50/18) = 2°F 24 x 25
Hence stack wall outer temperature = 400 — 134 — 2 = 264°F.
It can be shown that at a casing or wall temperature of 256°F, the heat loss through gas film matches the loss through the stack wall. The heat loss = 629 Btu/ft2 h, and total heat loss = 411,400 Btu/h.
411,400
Gas temperature drop =———————— = 14°F
F F 110,000 x 0.265
The average gas temperature = 410 — 14 = 396°F, which is close to the 400°F assumed. With a computer program, one can fine-tune the calculations to include fouling factors.
What are the effects of wind velocity and casing emissivity on heat loss and casing temperature?
Using the method described earlier, the casing temperature and heat loss were determined for the case of an insulated surface at 600°F using 3 in. of mineral fiber insulation. (Aluminum casing has an emissivity of about 0.15, and oxidized steel, 0.9.) The results are shown in Table 8.40.
How does one check heat transfer equipment for possible noise and vibration problems?
A detailed procedure is outlined in Refs. 1 and 8. Here only a brief reference to the methodology will be made.
Whenever a fluid flows across a tube bundle such as boiler tubes in an economizer, air heater, or superheater (see Fig. 8.24), vortices are formed and shed in the wake beyond the tubes. This shedding on alternate sides of the tubes causes a harmonically varying force on the tube perpendicular to the normal flow of the fluid. It is a self-excited vibration. If the frequency of the von Karman vortices, as they are called, coincides with the natural frequency of vibration of the tubes, resonance occurs and the tubes vibrate, leading to leakage and damage
|
Table 8.40 Results of Insulation Performance
|
|
FIgure 8.24 Crossflow of gas over tube bundles. (a) Water tube boiler design; (b) air heater; (c) superheater. |
At supports. Vortex shedding is more prevalent in the range of Reynolds numbers from 300 to 2 x 105. This is the range in which many boilers, economizers, and superheaters operate. Another mechanism associated with vortex shedding is acoustic oscillation, which is normal to both fluid flow and tube length. This is observed only with gases and vapors. These oscillations coupled with vortex shedding lead to resonance and excessive noise. Standing waves are formed inside the duct.
Hence in order to analyze tube bundle vibration and noise, three frequencies must be computed: natural frequency of vibration of tubes, vortex shedding frequency, and acoustic frequency. When these are apart by at least 20%, vibration and noise may be absent. Q8.59b-Q8.59e show how these values are computed and evaluated.
8.59b Q:
How is the natural frequency of vibration of a tube bundle determined?
The natural frequency of transverse vibrations of a uniform beam supported at each end is given by
(114a)
Where
C = a factor determined by end conditions E = Young’s modulus of elasticity
I = moment of inertia = p(dO" — df)/64 Me =mass per unit length of tube, lb/ft (including ash deposits, if any, on the tube)
L = tube length, ft
Simplifying (114a), we have for steel tubes
(114b)
Where do and d, are in inches.
Table 8.41 gives C for various end conditions.
|
Mode |
Of vibration |
||
|
End support conditions |
1 |
2 |
3 |
|
Both ends clamped |
22.37 |
61.67 |
120.9 |
|
One clamped, one hinged |
15.42 |
49.97 |
104.2 |
|
Both hinged |
9.87 |
39.48 |
88.8 |
8.59c Q:
How is the acoustic frequency computed?
A:
F is given by Vs/1, where Vs = velocity of sound at the gas temperature in the duct or shell, ft/s. It is given by the expression Vs = (g0vRT)0’5. For flue gases and air, sonic velocity is obtained by substituting 32 for g0, 1.4 for v, and 1546/MW for R, where the molecular weight for flue gases is nearly 29. Hence,
Vs = 49 x T0 5 (115)
Wavelength l = 2W/n, where W is the duct width, ft, and n is the mode of vibration.
How is the vortex shedding frequency f determined?
F is obtained from the Strouhal number S:
S =fed0/12V (116)
Where
D0 = tube outer diameter, in.
V = gas velocity, ft/s
S is available in the form of charts for various tube pitches; it typically ranges from 0.2 to 0.3 (see Fig. 8.25) [1].
Q8.59e shows how a tube bundle is analyzed for noise and vibration.
|
|
|
S TROU HAL NUMBER (S) ( IN-LINE ) |
|
Figure 8.25a Strouhal number for in-line bank of tubes. |
|
FIgure 8.25b Strouhal number for staggered bank of tubes. |
A tubular air heater 11.7 ft wide, 12.5 ft deep, and 13.5 ft high is used in a boiler. Carbon steel tubes of 2 in. OD and 0.08 in. thickness are used in in-line fashion with a transverse pitch of 3.5 in. and longitudinal pitch of 3.0 in. The heater is 40 tubes wide (3.5 in. pitch) and 60 tubes deep (2.5 in. pitch). Air flow across the
|
|
Tubes is 300,000 lb/h at an average temperature of 219°F. The tubes are fixed at both ends in tube sheets. Check whether bundle vibrations are likely. Tube mass per unit length = 1.67 lb/ft.
First compute fj;fe, andf,. L = 13.5 ft, do =2in., d, =1.84in., Me = 1.67lb/ft, and, from Table 8.41, C = 22.37.
Using Eq. (114b), we have
Fn = 90^ XP4 — 1 -84^4)0-5 = 18.2 Hz
(13.5)2 (1.67)
This is in mode 1. In mode 2, C = 61.67; hence is 50.2 Hz. (The first two modes are important.)
Let us compute f,. S from Fig. 8.25 For ST/do = 3.5/2=1.75 and a longitudinal pitch of 3.0/2 = 1.5 is 0.33.
From Eq. (1) of Chapter 5, p = 40/(219 + 460) = 0.059 lb/cuft.
Free gas area = 40 x (3.5 — 2) x 13.5/12 = 67.5 lb/ft2 h
(13.5 is the tube length, and 40 tubes wide is used with a pitch of 3.5 in.) Hence air velocity across tubes is
V =_____ ~_________ = 21 ft/s
67.5 x 3600 x 0.059 1
Hence
, 12SV 0.33 x 21
Fe = —-— =12 x——————- = 41.6 Hz
D0 2
Let us compute fa. T = (219 + 460) = 679°R. Hence Vs = 49 x 6790 5 = 1277 ft/s. Width W = 11.7 ft, and 1 = 2x 11.7 = 23.4 ft. For mode 1 or n = 1,
Fa1 = 1277/23.4 = 54.5 Hz
For n = 2,
Fa2 = 54.5 x 2 = 109 Hz
The results for modes 1 and 2 are summarized in Table 8.42. It can be seen that without baffles the frequencies fa and fe are within 20% of each other. Hence noise problems are likely to arise. If a baffle or plate is used to divide the duct width into two regions, the acoustic frequency is doubled as the wavelength or width is halved. This is a practical solution to acoustic vibration problems.
|
|
||||
|
|
|
|||
|
|
|||||
|
What are the other checks for ensuring that tube bundle vibrations are minimized? The vortex shedding frequencies often coincide with acoustic frequency, and often no standing waves develop and the transverse gas column does not vibrate. Resonance is more the exception than the rule. Chen proposed a damping criterion C based on tube geometry as follows [1]:
Where St and Sl are the transverse and longitudinal spacing and d is the tube diameter. The method of calculating the Strouhal number S is given in Q8.59d. For an in-line bank of tubes without fins, Chen stated that C must exceed 600 before a standing wave develops. A large variation in C exists in practice. According to one study, in spiral finned economizers C reached 15,000 before a sonic vibration developed. If C is less than 2000, then vibrations due to vortex shedding may not occur. Vibration analysis is not an exact science, and a lot of it is based on experience operating units of similar design. In some cases the calculations showed that the vortex shedding and acoustic frequencies were matching but no damaging vibrations occurred.
ASME Sec. 3 Appendix N 1330, 1995 on flow-induced vibration suggests that if the reduced damping factor C exceeds 64 where
|
(118) |
C = 4pmX/pd2
Then vortex shedding is unlikely to cause damage. This is due to the large mass of the system compared to the low energy in the gas stream. In Eq. (118),
M = mass per unit length of tube, lb/ft
X = damping factor (typically 0.001 for systems with no intermediate support and 0.01 for systems with intermediate supports) p = gas density, lb/ft3 d = tube OD, in.
Table 8.43 shows the results of calculations for a waste heat boiler that has both bare and finned tubes. The high gas temperature region at the entrance section has bare tubes, and the cooler section has finned tubes.
Coincidence of vortex shedding frequency with the natural frequency in the fourth mode is not a concern. Due to the low amplitudes at lower modes, tube damage is unlikely. Also, owing to the high value of C, which exceeds 64, vortex shedding is unlikely to cause tube damage.
The need for intermediate tube supports is governed by fluid elastic instability considerations. ASME Sec. 3 gives an idea of the stability of tube bundles. If the nondimensional flow velocity as a function of mass damping factor is above the curve shown in Fig. 8.26, then intermediate supports are required; without them fretting and wear of tubes due to vibration is possible. Basically this criterion tells us that if we have a tall tube bundle without intermediate supports, it can oscillate due to the gas flow; intermediate supports help to increase the natural frequency of the tubes and thus reduce the nondimensional flow velocity, making the bundle design more stable. Using the criterion showed that intermediate supports are required even for short boilers (under 12 ft high). However, based on my experience designing several hundred water tube waste heat boilers that are now in operation, the boilers operated well without intermediate supports, indicating once again the generality of these types of analysis. One has to consider operational experience of a similar unit along with these calculation procedures before modifying any boiler design.
|
Table 8.43 Damping Factors for Evaporator Tubes
|
|
5 — 0 —————— T—————— 1—————— T—————— T——- ~—1—————————————————————————————————— 1 1 1 1 1 10 20 30 40 50 60 70 80 90 100 Mass damping |
Figure 8.26 Damping factor versus nondimensional flow velocity.
In a boiler with mass per unit length m = 3.132 lb/ft, damping factor X = 0.001, gas velocity = 87 ft/s, and gas density p = 0.0188 lb/ft3, d = 2 in.
Mass damping factor = 2pmX = 2p x 3.132 x 0.001 x 144/(0.0188 x 22)
D2p
= 37.7
Nondimensional velocity = 12U/fd, where f = natural frequency of vibration, Hz; U = gas velocity, ft/s; and d = tube outer diameter, in.
Based on previous calculations, f = 20.6 Hz. Hence
Flow velocity = 87 x 12/(20.6 x 2) = 25.5
It can be seen from Fig. 8.26 that this is a borderline case and that an intermediate support would have further increased the natural frequency and made the flow velocity fall within the stable region. In practice, for tall tube bundles, intermediate supports at 11-15 ft intervals are used.
How are the gas properties Cp, m, and k estimated for a gaseous mixture? Determine Cp, m, and k for a gas mixture having the following analysis at 1650°F and 14.7psia.
|
Gas |
Vol% |
Cp |
M |
K |
MW |
|
N2 |
80 |
0.286 |
0.108 |
0.030 |
28 |
|
O2 |
12 |
0.270 |
0.125 |
0.043 |
32 |
|
SO2 |
8 |
0.210 |
0.105 |
0.040 |
64 |
Mixture properties are needed to evaluate heat transfer coefficients. For flue gas obtained from the combustion of fossil fuels, in the absence of flue gas analysis, one can use the data on air.
For a gaseous mixture at atmospheric pressure, the following relations apply. For high gas pressures, readers are referred to Ref. 1.
Mm = (nSa)
Km = Ј yk (119b)
W MW,- T CDi MW x yt
C — =PM Wx y? (119c)
Where
MW = molecular weight
Y = volume fraction of any constituent
Subscript m stands for mixture.
Substituting into Eqs. (119), we have
0.286 x 0.8 x 28 + 0.27 x 0.12 x 32 + 0.21 x 0.08 x 64 pm = 0.8 x 28 + 0.12 x 32 + 0.08 x 64
= 0.272 Btu/lb °F
0.03 x 281/^ x 0.80 + 0.043 x 321/3 x 0.12 + 0.04 x 641/3 x 0.08
Km =
281/3 x 0.80 + 321/3 x 0.12 + 641/3 x 0.08 = 0.032 Btu/ft °F
|
Mm |
0.108 x ffi x 0.8 + 0.125 x V32 x 0.12 + 0.105 x V64 x 0.08 ffi x 0.8 + ffi x 0.12 + p64 x 0.105 = 0.109 lb/ft h
How do gas analysis and pressure affect heat transfer performance?
The presence of gases such as hydrogen and water vapor increases the heat transfer coefficient significantly, which can affect the heat flux and the boiler size. Also, if the gas is at high pressure, say 100 psi or more, the mass velocity inside the tubes (fire tube boilers) or outside the boiler tubes (water tube boilers) can be much higher because of the higher density, which also contributes to the higher heat transfer coefficients. Table 8.44 compares two gas streams, reformed gases from a hydrogen plant and flue gases from combustion of natural gas.
How does gas pressure affect the heat transfer coefficient?
|
Table 8.44 Effect of Gas Analysis on Heat Transfer
|
|
AC = (Cp/m)0-4k°- 6; F = C°- 33 k0 ■ 67/m0 ■ 27. |
The effect of gas pressure on factors C and F for some common gases is shown in Figs. 8.27 AnD 8.28. It can be seen that the pressure effect becomes smaller at high gas temperatures, while at low temperatures there is a significant difference. Also, the pressure effect is small and can be ignored up to a gas pressure of 200 psia.
8.63 Q:
How do we convert gas analysis in percent by weight to percent by volume?
A gas contains 3% CO2, 6% H2O, 74% N2, and 17% O2 by weight. Determine the gas analysis in volume percent.
So/wft’on. Moles of a gas are obtained by dividing the weight by the molecular weight; moles of CO2 = 3/44 = 0.06818.
The volume of each gas, then, is the mole fraction x 100. Percent volume of
O2 = (0.5312/3.57563) x 100 = 14.86, and so on. One can work in reverse and convert from volume (or mole) basis to weight basis.
|
Gas |
W% |
MW |
Moles |
Vol% |
|
CO2 |
3 |
44 |
0.06818 |
1.91 |
|
H2O |
6 |
18 |
0.3333 |
9.32 |
|
N2 |
74 |
28 |
2.6429 |
73.91 |
|
O2 |
17 |
32 |
0.5312 |
14.86 |
|
Total |
3.57563 |
100 |
What is the effect of gas pressure and gas analysis on design of a fire tube waste heat boiler? Compare the following two cases. In case 1, reformed gas in a
|
FIgure 8.27 Effect of gas pressure on heat transfer—flow inside tubes. (From Ref. 1.) |
|
Figure 8.28 Effect of gas pressure on heat transfer—flow outside tubes. (From Ref. 1.) |
Hydrogen plant is cooled in a waste heat boiler, whereas in case 2, flue gas in an incineration plant is cooled. Maximum allowable heat flux is 100,000 Btu/ft2h.
Case 1. Reformed gas. Flow = 100,000 lb/h; gas pressure = 300 psig; gas analysis (vol%):
CO2 = 5, H2O = 30, N2 = 0.1, H2 = 52, CH4 = 2.9, CO = 10.
Case 2. Flue gas. Flow = 100,000 lb/h; gas pressure = atmospheric; gas analysis (vol%):
CO2 = 7, H2O = 12, N2 = 75, O2 = 6.
Steam is generated at 500 psig using 230°F feedwater. Blowdown = 2%. Use fouling factors of 0.001 on both gas and steam sides. Tubes are 1.5 in. OD and
1.14 in. ID. Material is T11 for reformed gas boiler and carbon steel for flue gas boiler. Saturation temperature is 470°F.
Calculations were done using the procedure discussed in Q8.10. The results are presented in Table 8.45. The following points may be noted:
The boiler is much smaller when the gas pressure is higher because of the high gas density.
The heat transfer coefficient is much higher for the reformed gas owing to the presence of hydrogen and water vapor. The heat flux is also very high compared to that in the flue gas boiler.
|
Table 8.45 Effect of Gas Analysis and Pressure on Design of Fire Tube Boiler
|
|
Waste gasa |
Temp (°C) |
Pressure (psig) |
Vol% component |
||||||||||||
|
N2 |
NO |
H2O |
O2 |
SO2 |
SO3 |
CO2 |
CO |
CH4 |
H2S |
H2 |
NH3 |
HCL |
|||
|
1 |
300-1000 |
1 |
80 |
10 |
10 |
||||||||||
|
2 |
250-500 |
1 |
81 |
11 |
1 |
7 |
|||||||||
|
3 |
250-850 |
3-10 |
66 |
9 |
19 |
6 |
|||||||||
|
4 |
200-1100 |
1 |
70 |
18 |
3 |
9 |
|||||||||
|
5 |
300-1100 |
30-50 |
0.5 |
37 |
6 |
8 |
5.5 |
43 |
|||||||
|
6 |
200-500 |
200-450 |
20 |
60 |
20 |
||||||||||
|
7 |
100-600 |
1 |
75 |
7 |
15 |
3 |
|||||||||
|
8 |
175-1000 |
1 |
72 |
10 |
6 |
12 |
Trace |
||||||||
|
9 |
250-1350 |
1 |
76 |
8 |
4 |
7 |
5 |
||||||||
|
10 |
150-1000 |
1 |
73 |
20 |
2 |
5 |
|||||||||
|
11 |
300-1450 |
1.5 |
55 |
23 |
6 |
6 |
3 |
3 |
4 |
|
A1, Raw sulfur gases; 2, SO3 gases after converter; 3, nitrous gases; 4, reformer flue gases; 5, reformed gas; 6, synthesis gas; 7, gas turbine exhaust; 8, MSW incinerator exhaust; 9, chlorinated plastics incineration; 10, fume or VOC incinerator exhaust; 11, sulfur condenser effluent. |
The tube wall temperature is also higher with reformed gas. Hence steam- side fouling should be low in these boilers.
It is obvious that gas analysis and pressure play a significant role in the design of boilers. Table 8.46 gives the analysis and gas pressure for typical waste gas streams.
|
A Af ; At; Ai; Ao Aw B B C CP C1-C6 D D, dt e E F Ff F G H Hc Hi, ho Hlf HN Ah Km K1, K2 |
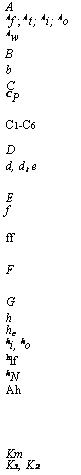Surface area, ft2
Fin, total, inside, and obstruction surface areas, ft2/ft Area of tube wall, ft2/ft Factor used in Grimson’s correlation Fin thickness, in.
Factor used to estimate heat transfer coefficient
Specific heat, Btu/lb °F; subscripts g, w, m stand for gas, water,
And mixture
Factors used in heat transfer and pressure drop calculations for finned tubes Exchanger diameter, in.
Tube outer and inner diameter, in.
Escalation factor used in life-cycle costing calculations; base of natural logarithm Efficiency of HRSG or fins
Frequency, Hz or cps; subscripts a, e, n stand for acoustic, vortex shedding, and natural
Fouling factor, ft2h °F/Btu; subscripts i and o stand for inside and outside
Factor used in the estimation of outside heat transfer coefficient and in the estimation of capitalized costs Gas mass velocity, lb/ft2 h Fin height, in.
Convective heat transfer coefficient, Btu/ft2h °F
Heat transfer coefficients inside and outside tubes, Btu/ft2h °F
Heat loss factor, fraction
Nonluminous heat transfer coefficient, Btu/ft2h °F Change in enthalpy, Btu/lb Interest rate
Thermal conductivity, Btu/fth °F or Btu in./ft2h °F; subscript m stands for mixture
Metal thermal conductivity, Btu/fth °F Constants
L Length, ft; thickness of insulation, in.; or beam length
Le Equivalent thickness of insulation, in.
M Factor used in Eq. (47, 51)
Mc Water equivalent, Btu/°F
Me Weight of tube, lb/ft
MW Molecular weight
N Number of fins per inch
N Constant used in Grimson’s correlation; also number of tubes
Nu Nusselt number
NTU Number of transfer units
P Term used in temperature cross-correction
Pw, Pc Partial pressure of water vapor and carbon dioxide
Pr Prandtl number
Q Energy transferred, Btu/h; heat flux, Btu/ft2 h
Q Heat flux, heat loss, Btu/ft2 h
Qc Critical heat flux, Btu/ft2 h
R Thermal resistance, ft2h °F/Btu; subscripts z, o, and t stand for
Inside, outside, and total Re Reynolds number
Rm Metal thermal resistance, ft2 h °F/Btu
S Fin clearance, in.; Strouhal number; surface area, ft2
ST, SL Transverse and longitudinal pitch, in.
T Fluid temperature, °F; subscripts a, s, b stand for ambient,
Surface, fin base tf Fin tip temperature, °F
Tm Metal temperature, °F
Tsat Saturation temperature, °F
T Absolute temperature, K or °R; subscripts g and w stand for gas
And wall
AT Log-mean temperature difference, °F
U Overall heat transfer coefficient, Btu/ft2 h °F
V Fluid velocity, ft/s or ft/min
Vs Sonic velocity, ft/s
W Fluid flow, lb/h; subscripts g, s, w stand for gas, steam, and
Water
W Flow per tube, lb/h
X Steam quality, fraction
Y Volume fraction of gas
E Effectiveness factor
Ec, ew, eg Emissivity of CO2, water, gas emissivity
As Emissivity correction term
Z Fin effectiveness
M Viscosity, lb/ft h; subscript m stands for mixture
P gas density, lb/cu ft
L wavelength, ft
V ratio of specific heats
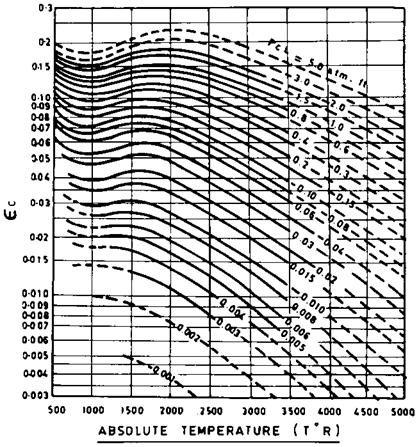
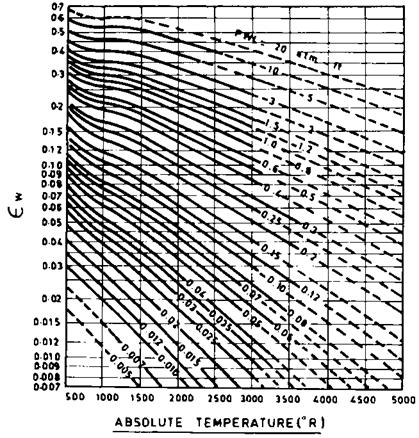
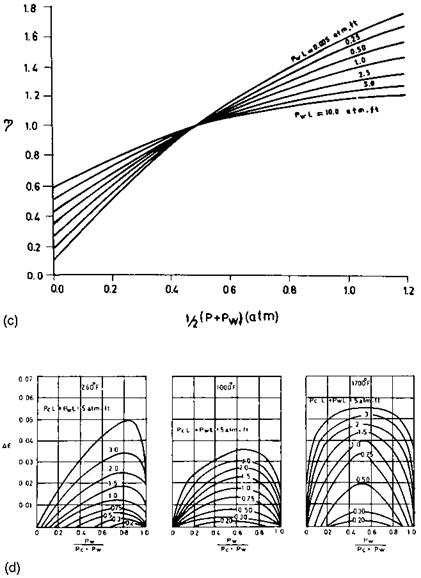
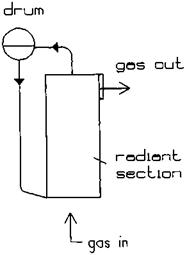
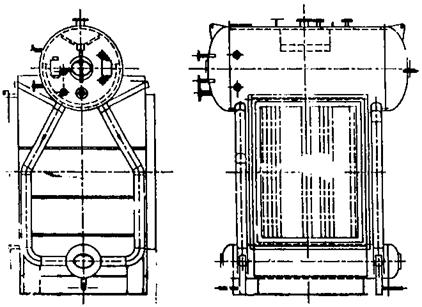
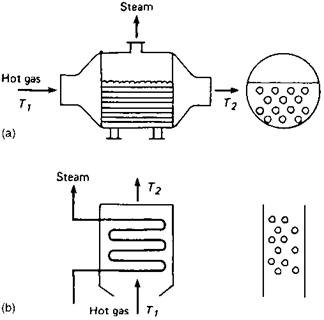
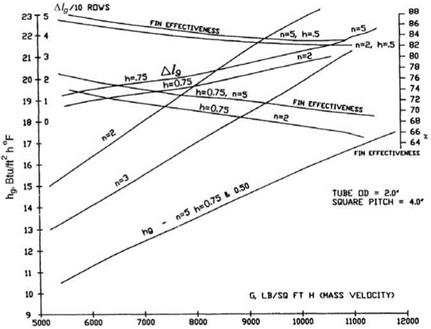
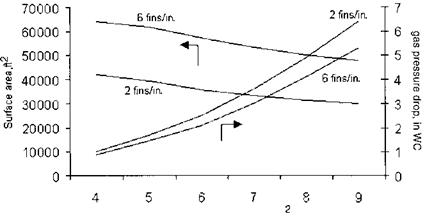
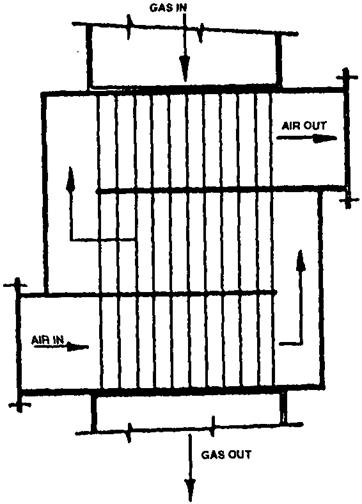
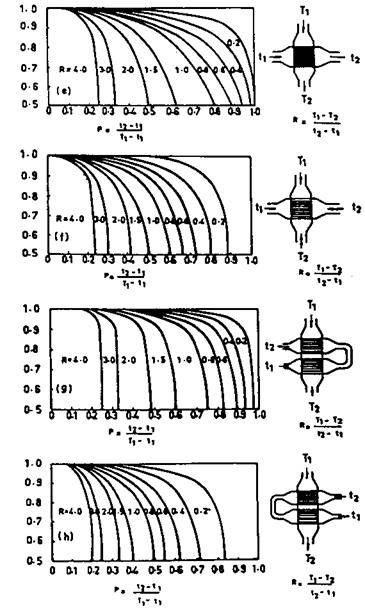
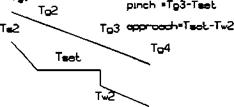
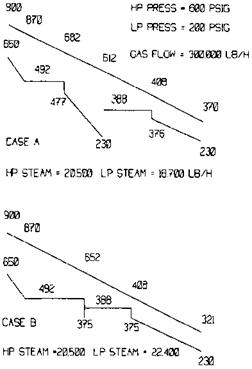
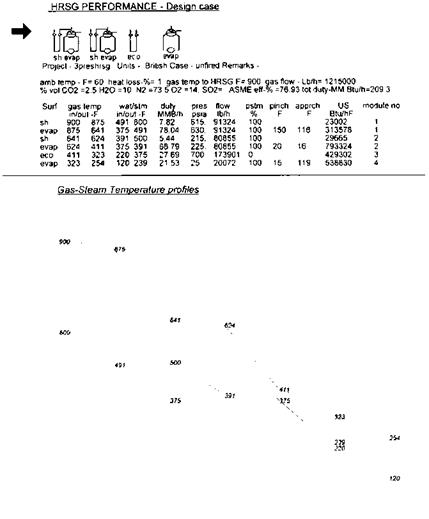
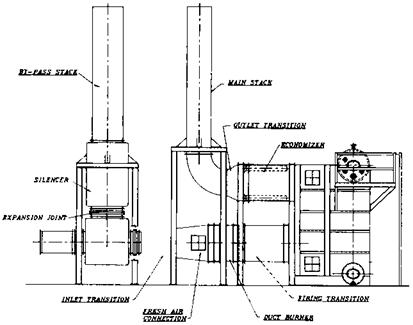
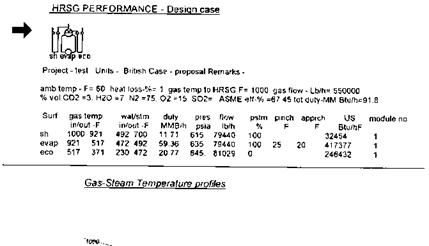
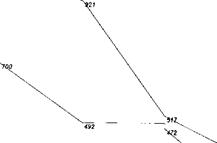
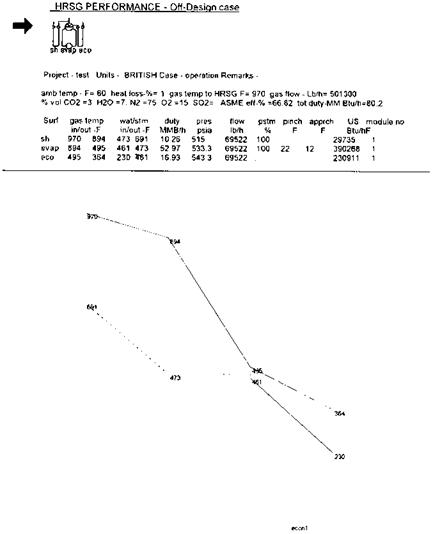
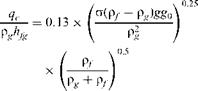
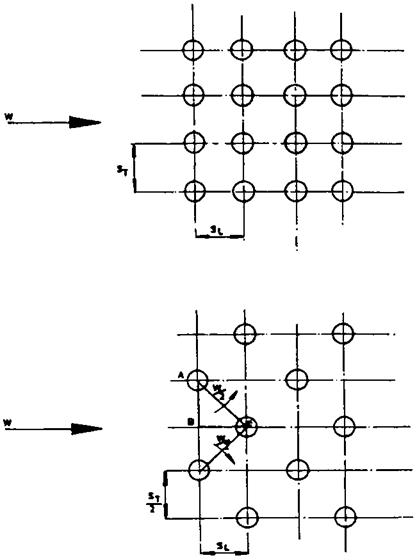
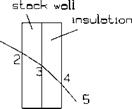
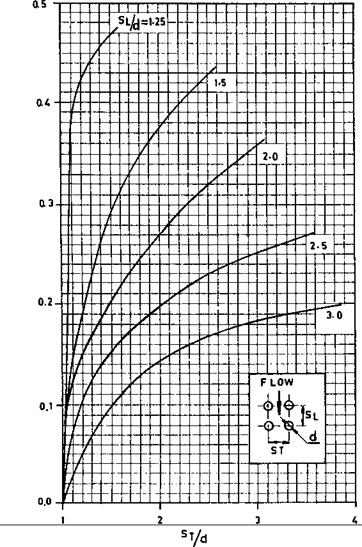
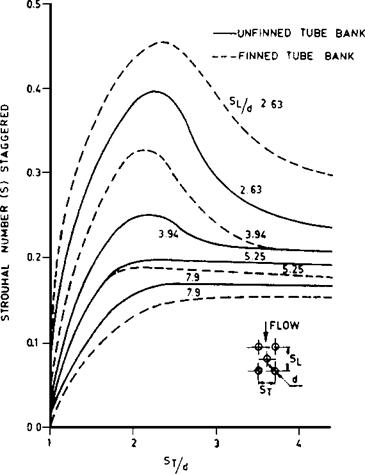
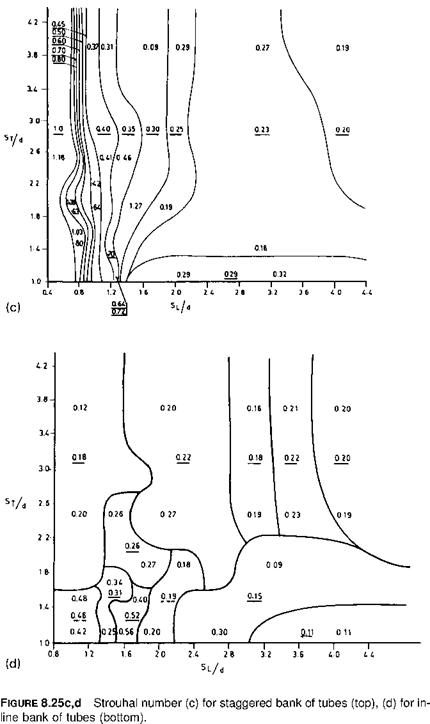
Опубликовано в рубрике 
