13 августа, 2013 
admin Heat transfer deals with the transmission of thermal energy from higher — to lower level by any one or a combination of the three classical modes, namely, conduction, convection, and radiation. The fundamentals of these heat transfer processes are individually simple, but the applications are complex because of the simultaneous occurrence of several modes of heat transfer, irregular shapes involved, dynamic conditions, and so on. That is why heat transfer is a not-so-exact science, as the variables are many and the situations dynamic. Also, a very large body of data on fundamental properties of materials is required.
1. Conduction is the transfer of heat from one part of a body to the other or from one body to another in physical contact. It is the flow of energy that occurs in a substance without appreciable movement of molecules due to lattice vibrations and flow of free electrons. Heat flow from flue gases to water/steam across the metal wall in a boiler, loss of furnace heat to the surrounding atmosphere through insulation, and heat loss from hot steam/water pipes through insulation are all examples of conduction.
2. Convection is the flow of energy from the surface to the surrounding fluid due to conduction and mixing of fluid molecules. It is the transfer of heat
A. From one point to another within a fluid due to its movement or
B. From one fluid to another by mixing of fluids or
C. Between a solid and a fluid through a relative motion between them
Heat flow from flue gases to tube banks and heat loss from the lagging of boiler or pipe are examples of convection.
Convection can take place in
A. A single phase as in forced or free convection.
I. Forced convection. An external force moves the fluid over the surface. The velocities and the resultant heat transfer rates are naturally higher.
Ii. Free convection. Only a natural force is at work, such as gravity or buoyancy. The velocities and the heat transfer rates are lower.
B. Two phases as in boiling or condensation
I. Boiling. When a liquid absorbs heat from a surface, which is at a temperature higher than the saturation temperature, there is a change of phase as the liquid turns into vapor; this is called boiling. ii. Condensation. When a vapor gives out heat in contact with a surface, which is at a temperature lower than the saturation temperature, there is a change of phase as the vapor turns into liquid; this is called condensation.
3. Radiation is the transfer of heat by electromagnetic waves from the surface without the need of any medium. Heat flow in a boiler furnace is almost entirely by radiation.
The general equation for heat flow is
|
(2.1) |
Q = UAAt
Or
AAt
R
Where
|
Q U A At R |
Rate of heat flow in Watts or kilocalories per hour (Btu/h)
Overall heat transfer coefficient in Watts per square meter degree Celsius or
Kilocalories per square meter hour degree Celsius (Btu/ft2 h °F)
Surface area in square meters (ft2)
Temperature difference causing flow in degree Celsius (°F)
1/U, the overall combined resistance
The presence of a temperature gradient is essential for conduction to take place. The heat flow and the temperature gradient are related as defined in Fourier’s law, which states that the rate of flow of heat flux by conduction in any direction is directly proportional to the temperature gradient present in that direction.
Q tj -12
TOC o "1-5" h z —oc—1——————- 2
A = (2.2)
where k is the constant of proportionality called thermal conductivity.
Thermal conductivity can be defined as the rate of flow of heat flux caused by unit temperature difference. It follows that the heat flow by conduction is governed by the equation
KA(tj -12)
Q = —- (2.3)
Where
K = thermal conductivity in Watts per meter degree Celsius or kilocalories per square meter per degree Celsius per centimeter (Btu/ft2 h °F/in. or Btu/ft2 h °F/ft)
L = thickness of plate in centimeters (ft or in.)
A = area in square meters (ft2)
(tj — t2) = temperature gradient in degree Celsius (°F)
Certain interesting aspects of thermal conductivity are as follows:
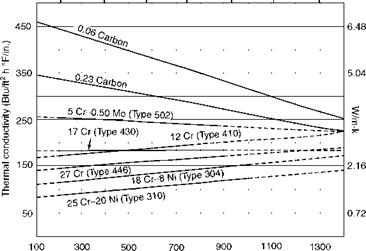
• Metals are good conductors, and refractory and insulating materials are bad conductors (with low conductivity). k for pure metals is the highest and decreases with the rise in impurities. The range of k is given in Tables 2.2 and 2.3.
• With increase in temperature the thermal conductivity of
— Most pure metals decreases with the exception of aluminum and uranium
— Alloys may increase or decrease
— Insulating materials generally increases
— Most liquids reduces, with the exception of water due to the decrease in density
— Gases increases
• Heat transfer by conduction in fluids is small in comparison with convection and obeys the same laws as solids.
|
TABLE 2.2 TABLE 2.3 K Values of Common Materials at Room Temperature Range of k Values for Materials
|
|
Temperature (°C) 0 200 400 600 800 1000 1200 1400 1600
Gas temperature (°F) FIGURE 2.8 Thermal conductivity (k) of air and flue gas at various temperatures. |
• The variation in thermal conductivity with temperature is almost linear for most materials as given by the equation (Figures 2.8 and 2.9)
K = k0(1 + pt) (2.4)
Where k0 is the thermal conductivity at 0°C and p is the temperature coefficient of
Thermal conductivity. p is +ve for nonmetals and insulating materials (with the exception of magnesite) and — ve for metals (with the exception of aluminum and certain nonferrous materials).
• k for water changes by just over 50% from 0°C to critical point.
• k for gases increases with increasing temperature.
• Good conductors of heat are also good conductors of electricity. The ratio of thermal and electrical conductivities is the same for all metals at the same
|
Temperature (°C) 100 200 300 400 500 600 700
Temperature (°F) FIGURE 2.9 Thermal conductivity (k) of select boiler metals at high temperatures. |
|
_k_ CtT |
Temperature, and the ratio is directly proportional to the absolute temperature of the metal.
Constant
Heat transfer by convection between a fluid and a solid is governed by
|
(2.5) |
Q = UcA(t1 — t2)
Where Uc is the convection film conductance in Watts per square meter degree Celsius or kilocalories per square meter hour degree Celsius (Btu/ft2 h °F).
Free or natural convection is the heat transfer that occurs due to the movement of fluid particles caused by density changes associated with temperature differential in a fluid. Heat transfer by free convection, for example, on the outside of a clad surface, where the surface temperature difference sets up a thermal current, is calculated by Equation 2.5 with free-convection film conductance taken as
|
(2.6) |
Ufc = C(tj — t2)1/3
Where C is the coefficient depending on shape and position and (t1 — t2) is the temperature difference between the surface and fluid (air). Here the flow velocities and coefficients are much lower in comparison with the forced convection.
The coefficient of heat transfer in forced convection depends on a number of variables, namely viscosity (p), density (p), thermal conductivity (k), specific heat (Cp), and velocity (v).
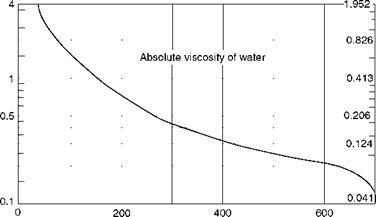
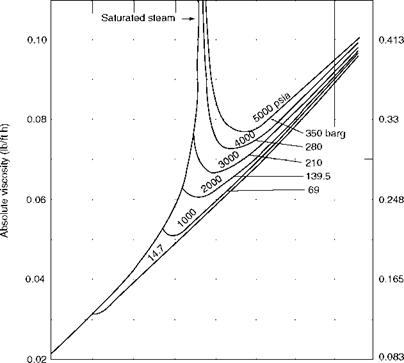
Viscosity (p) (absolute or dynamic) is the property of the fluid that determines its resistance to shearing stresses. It is a measure of the internal fluid friction that causes resistance to flow. Viscosity can also be defined as the shear stress to produce unit rate of shear strain. The unit of viscosity is Newton seconds per square meter (N s/m2) or kilograms force seconds per square meter (kgf s/m2) or pounds force seconds per square feet (1b fs/f 2). In CGS units the measure is dyne seconds per square centimeter or poise. The viscosity of water at 20°C is 1 cP. Figures 2.11 and 2.12 depict the absolute viscosity of water and steam, respectively.
Kinematic viscosity (v) is the ratio between the absolute or dynamic viscosity and the density of fluid, that is, v = |/p. The unit is the square centimeter per second (cm2/s) (Stoke) or square meter per second (m2/s) or square feet per second (ft2/s).
1 cSt = 1/100 St = 100 mm2/s
Heat transfer data and fluid flow phenomena are correlated with the help of dimension — less numbers and the coefficient of heat transfer is deduced. The important dimensionless numbers are
1. Reynolds number (Re) indicates the type of flow—viscous or turbulent. Osborne Reynolds demonstrated, with a simple experiment of passing a mixture of water and dye of the same specific gravity through a horizontal glass tube, that three regimes of flow exist—laminar, turbulent, and transition flows, depending on the predominance of viscous or inertial forces. Figure 2.10 depicts the flow of dye in all the three regimes.
A. Reynolds number represents the ratio of inertial to viscous forces.
B. Inertial forces are roughly proportional to the square of velocity, and viscous forces to the first power. Loss of pressure head is approximately proportional to v2 in turbulent flow and v in laminar flow.
|
Straight
|
|
Transition flow
Turbulent flow |
FIGURE 2.10
Types of flow.
C. At low velocities (Re < 2000) the viscous forces dominate, resulting in a viscous or laminar flow, whereas at high velocities (Re > 4000) inertial forces dominate resulting in a turbulent flow.
|
(2.7) |
|
Re |
GD _ pvD |j |j
Where
G = mass velocity in kilograms per square meter hour D = pipe diameter in meters
H = absolute fluid viscosity in kilograms per meter hour p = density in kilograms per cubic meter v = velocity in meters per second
Equation (2.7) can also be rewritten as
|
Pv |jv/D |
|
(2.8) |
Internal force
Or
Viscous force
Figures 2.11 and 2.12 depict the absolute viscosity of water and steam, respectively.
2. Prandtl number (Pr) is primarily a measure of ease of heat transmission through the fluid. It is also a ratio of momentum diffusivity to thermal diffusivity.
C
|
(2.9) |
|
Pr |
Cp k
A. It represents temperature gradient similarity.
B. It can be rearranged as
|
(2.10) |
|j/p _ kinematic viscosity k/ pCp thermal diffusivity
|
|
|
93 |
|
Temperature (°C) 204 |
|
316 |
|
> W |
|
O ■O |
|
Temperature (°F) |
FIGURE 2.11
Absolute viscosity of water.
|
Temperature (°C) 204 427 650 870
400 800 1200 1600 Temperature (°F) FIGURE 2.12 Absolute viscosity of steam. (From Babcock and Wilcox Company, U. S.A. With permission.) |
C. It can be considered as specific heat Cp divided by k/|a, the ratio of thermal conductivity to viscosity. A high conductivity or low viscosity helps to stimulate heat flow.
3. Nusselt number (Nu) is basically a ratio of heat transfer by convection to heat transfer by conduction.
Nu = UcD (2.11)
K
It is also the ratio of the size factor to the thickness of the boundary layer k/Uc.
4. Stanton number (St) is the ratio of heat absorbed to that available for absorption.
St=CUg (212)
The ratios are related as Nu = St Re Pr.
5. Grashoff number (Gr) is the ratio of the product of the inertia force and the buoyancy force to the square of viscous forces. Gr has a role in free convection, similar to that of Re in forced convection. Free convection increases with increase in Gr.
In the absence of a uniform free stream temperature, there is a need to use a mean temperature that can be either of the following:
1. Mean film temperature (Tmf) as used for fluid flow over flat surfaces, that is, the arithmetic mean of the surface temperature of the plate (Ts) and the undisturbed film temperature (Tf) of the fluid flowing across it
T = Ts + Tf f 2
2. Bulk mean temperature as used for fluid flow inside pipes or ducts, that is, the arithmetic mean of the bulk inlet and bulk outlet temperatures
(Tb. + Tb )
V D, n bont ‘
T — v bin________ bout ‘
Tmb
2
For both horizontal and vertical tubes, the convection conductance for laminar flow Ucl in kilocalories per square meter per hour per degree Celsius (British thermal units per square feet per hour per degree Fahrenheit) is given by the empirical formula derived by McAdams
UC = X (Z)“ ( ^ D )’,J (2,3)
Where |js is the viscosity at the surface temperature and L is the heated length of straight tube.
For both heating and cooling of fluids inside clean conduits, Ucl (the convection conductance in turbulent longitudinal flow) is developed from the following equations:
Nu = 0.023Re08Pr04 (2.14)
Ud = Uci FppFt (2.15)
Where
U’cl = basic convection conductance in longitudinal flow 0.023G0.8/D;02 Fpp = physical properties factor Cp04k04/|a04 at film temperature
Ft = temperature factor (Tfilm/Tbulk)0-8, where Tf is (average surface temperature +
Average bulk temperature)/2
Turbulent Flow Outside Tubes (Cross Flow)
This is developed from the following equation:
Nu = 0.287Re061 Pr033Fa (2.16)
UCc = U’ccFppFaFd
Where
U’cc = basic convection conductance in cross flow 0.287 G061/Dl039 Fpp = physical properties factor (Cp033k067)/^028 at film temperature
Fa = tube arrangement factor depending on Re and tube spacing Fd = depth factor
Turbulent Flow Outside Tubes (Longitudinal Flow)
This is derived from flow inside the tubes, with the tube of inner diameter Di substituted by the equivalent diameter De, which is
4(L^2 — 0.785Do2)/nDo
Where Lj and L2 are tube pitches and Do = the tube OD.
Figure 2.13 illustrates the flow of gases outside and inside the tube bundle in cross and longitudinal manners.
Every surface emits electromagnetic waves in all directions. Radiation is the heat transfer in which energy flows in the form of electromagnetic waves. The principles of radiation are as follows:
• Heat incident on a surface is absorbed, transmitted, or reflected, and the respective fractions are known as absorptivity, transmissivity, and reflectivity. The sum of the three is always unity.
• Bodies that are good absorbers are equally good emitters of radiation.
• A blackbody absorbs the entire radiation incident on it and does not reflect or transmit any part of it. No actual bodies are completely black.
• A white body fully reflects, whereas a transparent body fully transmits the entire incident radiation. An opaque surface does not transmit any radiation.
• When a surface is in thermal equilibrium with its surroundings, the emissivity of the surface equals its absorptivity. This is known as Kirchoff’s law.
• Emissive power is the radiant flux from the surface at a particular temperature.
• The radiation emitted by a blackbody is proportional to the fourth power of its absolute temperature and surface area. This is known as the Stefan-Boltzmann law.
|
(2.17) |
Q = ctsST4
Where
Ct = Stefan-Boltzmann constant e = emissivity
|
FIGURE 2.13 Cross and longitudinal flows outside tubes and longitudinal flows through tubes. |
S = area
T = absolute temperature
• e is the ratio of heat emitted by a body to the heat emitted by a blackbody at the same temperature.
• The radiation from a blackbody extends over a whole range of wavelengths but remains concentrated over a narrow range.
• A number of commercial surfaces have emissivities of 0.8-0.95 and behave like blackbodies.
When two blackbodies at temperatures T and T2 (where T > T2) exchange heat, the heat flow from body 1 to body 2 is
Q12 = Fl2°S1(T14 — T24)
Where F12 is the angle factor depending on the geometry. Emissivity factor and angle factors are further suitably added in this equation. Heat transfer in furnaces is substantially by radiation. With most fuels, the radiation is luminous. Only a few gases like the blast furnace gas (BFG) exhibit nonluminous radiation.
Gases like CO, CO2, SO2, and water vapor absorb and emit radiation at certain wave lengths outside the visible range. Nonluminous radiation is rarely encountered in a furnace, whereas it is always present in the intertube heat transfer in SH, RH, and convection banks at temperatures higher than ~400°C.
In practice, heat transmission involves the combination of any two or all three heat transfer mechanisms. The individual conductances (Us) are combined into a single conductance similar to the electrical circuitry. Resistance R = 1/U and the resistances are added when in series to arrive at the overall resistance.
A clean tube wall separated by two fluids on either side is an example. The overall resistance
R = Rj + R2 + R3
Where 1, 2, and 3 represent the outside film, tube metal, and inside film resistances, respectively.
111 1 1 d=
U Uco 2k do log (do/d,) Uc. do
111
— = — + — (2.18)
U Uc Uc.
Co ci
Ignoring the metal resistance that is very small in comparison to the film resistances
Uc
U = Uc X — ci
Uc + Uc
A tube bank receiving heat from gas by convection and nonluminous radiation is an example. The overall resistance
R = (————— 1———— V + Rtw + Rcs (2.19)
((1/Rrg) + (1/Rcg))
Where
Rrg = gas film resistance to radiant heat flow
Rcg = gas film resistance to the convection heat flow
Rtw = resistance of tube wall to conduction heat flow
Rcs = resistance of the cold fluid film to convection heat or ignoring the tube metal resistance
111 ‘ (2.20)
U (Urg + Ucg) Ucs
This is the method to calculate the heat transfer coefficients for most boiler, SH, RH, ECON, and AH surfaces. Since accuracy is important, the tube wall resistance should also be included. The standard heat flow Equation 2.1 is applied, with At changed to Atm
Q = UAAtm
Where Atm is the log mean temperature difference (LMTD) causing the flow
= (At! — At2) (2.21)
M loge (Ati/At2)
Where At1 and At2 are the initial and final temperature differences. A graphic solution is presented in Figure 2.14.
The log mean temperature difference is the hypothetical temperature difference which, when maintained constant along the HX results in the same rate of heat flow as that obtained through the actual heat exchange.
The effectiveness of HX is the ratio of actual heat flow from the exchanger to the maximum possible heat that can be achieved if one of the fluids can be made to undergo the maximum possible change in temperature.
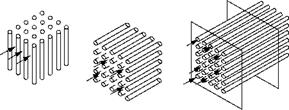
Inadequate HS with the subsequent temperature drop and low convective heat transfer is caused by use of extended or finned surfaces. Fin tubes employed in ECONs and heat recovery steam generators (HRSGs) are examples. Some common shapes are shown in Figure 2.15, but several configurations are possible. For proper fin design the knowledge of temperature distribution along the fin is necessary.
Fin effectiveness or efficiency is the ratio of the amount of actual heat transferred to the maximum possible heat transfer if the entire fin area is at the base temperature.
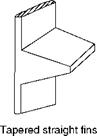
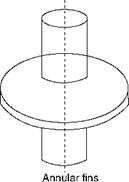
Straight or rectangular fins are the most popular as they are both easy and economical to manufacture, are light in weight, and offer minimum resistance to flow. Economizers for coal firing applications employ straight fins along tube axes. Tapered fins are of great practical importance as they give the maximum heat flow per unit weight. Annular fins
|
Kl |
|
20 |
|
100 = |
100 = |
100| |
|
90 1 |
90 |
90 |
|
80 1 |
80 |
80 |
|
70 ! |
70 |
70 |
|
601 |
60 |
60 |
|
50 |
50 |
50 |
|
40-= |
40 |
40 |
|
-= |
-= |
-j |
|
30-E |
|
30 |
20-
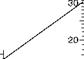
The nomogram is used for determining the mean logarithmic temperature difference:
Atgr — At
M
H(At — Ay
For a parallel or counterflow heat exchanger, Atgr and AtM indicate temperature differences
In the flowing media at either end of the heat exchanger.
Related values of Atgr, AtM, and Atm are joined on the nomogram by a straight line, as the following example illustrates:
With Atgr = 31°C on the right-hand scale and Atw = 7°C on the left-hand scale, the value
Atm = 16°C on the centre scale.
The nomogram is equally applicable to multiples of the values shown on the scales and may thus be used for (e. g.) °F.
|
|
||
|
|||
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
|
FIGURE 2.14
Graphical solution for LMTD.
|
|
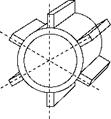Spines
|
|
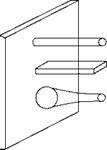Pin fins
FIGURE 2.15
Common fins.
Are used extensively in the HRSGs. Studs are employed very commonly in many areas of boilers, notably for holding the refractory and simultaneously transferring heat.
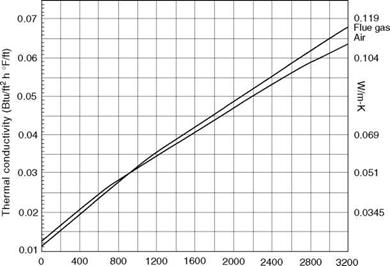
Опубликовано в рубрике 
