В соответствии с общей постановкой задачи, изложенной в предыдущем параграфе, представим фронт пламени в потоке однородной газовой смеси в виде поверхности сильного разрыва. На такой
|
|
Поверхности косого теплового скачка [Л. 28] происходят в результате сгорания свежей смеси мгновенное тепловыделение и нагрев продуктов сгорания до максимальной температуры. На ней претерпевают разрыв скорость потока, давление, температура и др. Схема такого фронта пламени представлена на рис. 7-1. В общем случае угол между вектором скорости набегающего потока и нормалью к поверхности разрыва (угол падения) может принимать любое значение в пределах от О до я/2. Значение О отвечает наиболее интенсивному тепловому скачку, расположенному под прямым углом к потоку свежей смеси (прямой скачок). Значение я/2 соответствует вырождению скачка в тангенциальный разрыв, т. е. отсутствию горения.
Заметим, что в этих двух крайних случаях (аг = 0, аг = я/2), и только в них, линии тока не будут преломляться на фронте и поток не будет отклоняться от прежнего направления. Во всех остальных {промежуточных) случаях вектор скорости за фронтом
повернется относительно прежнего направления на некоторый угол отклонения
З = «1 — «2.
Где а2 — значение угла между вектором и2 и нормалью к фронту — угла преломления. Для теплового скачка всегда а2 < сц. Иначе говоря, отклонившийся после фронта пламени поток газа сближается с нормалью к фронту в противоположность тому, что происходит при адиабатическом скачке.
При плавном изменении значения угла падения ах от 0 до я/2 и неизменном значении тепловыделения вместе с углом а1 будут меняться расчетные значения всех кинематических и динамических характеристик — угла преломления а2, угла отклонения б, отношения значений скорости и давления до и после фронта и др. Все они, за исключением одного только угла отклонения б, будут меняться монотонно. И только значение б, равное нулю при а1 — О и at = я/2, пройдет при некотором промежуточном между 0 и я/2 значении угла падения at = сх1# через максимум б = б^.
Поскольку опыт свидетельствует об однозначности эффекта, так как при заданном значении теплотворности смеси, а также всех величин до фронта угол а, г всегда принимает одно и то же значение, можно предположить, что это значение аг = аы. Иначе говоря, кажется правдоподобным, что реализуется именно то единственное значение угла отклонения б*, которому соответствует только одно значение угла аг = aljf. Это предположение положено в основу приведенного ниже расчета. Физическое толкование его будет дано ниже.
|
(7-1) |
Рассмотрим сперва количественную сторону вопроса. Запишем в качестве исходных уравнений условия сохранения массы, импульса (в проекции на нормаль и касательную к фронту пламени) и энергии при пересечении газом поверхности разрыва. Для простоты газ будем считать идеальным (Р = рRT) и пренебрежем изменением состава и теплоемкости при горении. Обозначим индексом 1 значения переменных до фронта и индексом 2 — за фронтом, а также индексами nut — соответственно нормальный и касательный к фронту компоненты скорости. Уравнения сохранения при этом имеют вид:
Plunl = р2«я2>
Р1 + Рі"л1 = Р2 + Р2"2„2 • ип = И/2 = и,
|
|
2ср Ср
В этих равенствах ипі — щ cos 2ах (для і = 1,2); Q — тепловыделение на единицу смеси.
В качестве безразмерной характеристики тепловыделения введем отношение величины Q к полной энтальпии газа до фронта,
Рассчитанной по нормальному к фронту компоненту скорости: Q Q
<7 =
, т, Unl ctJi+і———————- 1-М,[18] COS2 а,
СРТ 1 + р 1 2 1 1
„2
Где у = cp/cv] М = ы/а — число Maxa; а = V^RT — местная скорость звука.
Для М? < 1 (и тем более для М2 cos2а х 1, так как в опыте значение угла сравнительно близко к я/2) можно приближенно принять:
(7-2)
СрТі 7
Поскольку отношение давлений при М? 1 близко к единице, в том же приближении будет
TOC o "1-3" h z if«L = iL = J»_. 1 + (7.3)
«пі Рг Ті Рг Тх 4 V ‘
Из закона «преломления» (см. рис. 7-1) следует, что
"2 _ Sill ах Мл2 _ tg аі _ і і _ in а
И ‘ и І 1 Т
"і sm ог2 иш tg aj
|
1 + |
В общем случае при произвольном расположении теплового скачка отношение u<Juy, а также другие характеристики разрывного течения будут функциями двух параметров — угла падения аг и относительной теплотворности смеси q. Например, отношение продольных компонентов скорости (в направлении вектора скорости потока свежей смеси) будет равно
И*2 _ "*2
"*1 "1 1 + tg2 ах
Относительное изменение давления выразится в виде
Pl"P2 = q COS2 а ИЛИ р1~ р* « т М2 q cos2 at
Запишем также выражения для угла отклонения
Tg8 = tgK — а,) = (7-5)
1 + Я + tg® «і
И для относительной скорости распространения фронта WT = ип
—2- = cosa1.
В случае, когда а = аы и б «= б^ при максимальном преломлении линии тока, расчетные соотношения упрощаются. Угол
падения определяется при этом равенством
Tg«i* = Vі + <?•
А максимальный угол отклонения
Tg§* =
2 + Я ‘
|
(7-6) |
Так что значения этих углов связаны между собой простым равенством
= 2ч* ~
На рис. 7-2 для нескольких значений q показаны кривые зависимости 6 = 6 (а1, &) и прямая, проходящая через максимумы значений угла отклонения. Этому
Случаю (максимум преломления) отвечают простые формулы:
Для изменения модуля скорости
-^1=1/Т+7; (7-7)
Для изменения продольной составляющей скорости
!**.) — 2-i-i-l; (7-8) )t 2 + q v ‘
Для изменения плотности тока I Р2«2 1
(7-9)
РіИі К УУ+я
Для изменения давления Pi — Рг
(7-10)
Z/2
Для зависимости скорости распространения фронта от теплотворности горючей смеси
|
(7-11) |
УЛ 1 Ul К V* + q’
Наиболее примечательно то, что при аг = аи отношение (pjU^Pi"?), = 1> т — е — значение плотности потока импульса (по модулю вектора скорости) не меняется в скачке.
Конечно, полученные в расчете закономерности (в частности, рост угла аы и снижение скорости распространения разрыва WT при увеличении теплотворности q) отвечают принятой предельной схеме явления — бесконечно большой скорости реакции и отсутствию отвода тепла к свежей смеси.
Заметим, что для горения смеси углеводородов с воздухом (при Т да 300° К) значение q ^ 6. Для q = 6 имеем
|
"2 |
|
2,65, |
|
1,75, |
67 — 48°,
Pi — р2 р, и
В этом случае, как видно из приведенных значений, фронт пламени в расчетных условиях максимального отклонения (для зна-
|
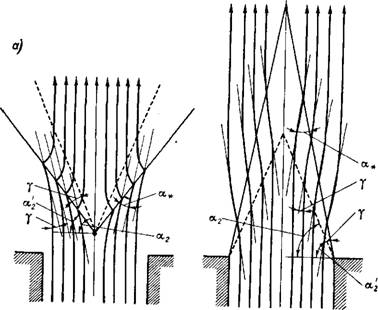
Рис. 7-3. Схема фронта пламени при горении однородной смеси: а — за стабилизатором; б — на бунзеновской горелке. |
Чения <7 = 6) располагается сравнительно круто. Обращает на себя внимание заметный рост продольной скорости их2 сравнительно со значением ult а также то, что перепад давления на фронте соизмерим со скоростным давлением набегающего потока.
|
0,75. |
Для сравнения с опытом приведем схему гомогенного факела с прямым и обращенным фронтами пламени (рис. 7-3). Опыт примерно соответствует значению q = 6. Расчетное значение = 67° заключено между значениями аг = 60° и а2 да 83° соответственно для прямого и обращенного факелов. С качественной стороны это расхождение можно объяснить искривлением линий тока в связи с разогревом свежей смеси при подходе к фронту. Как видно из
фотографий на рис. 7-4, для прямого конуса пламени следует ожидать значения aj а для обращенного а1 а1:}., поскольку расчетное значение а1# относится к невозмущенному потоку свежей смеси Таким образом, характер отклонения от расчета согласуется с опытом.
На рис 7-3 представлена фі пгография обращенного факела, в который вводились для наблюдения за изменением скорости на фронте
|
|
|
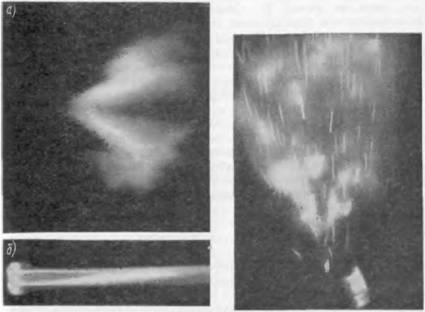
Рис. 7-4. Флтої рафии факела при горении однородной смеси: а — за стабилизатором; б — на бунзенов — ской горелке. |
|
Рнс 7-5. Фотография треков частиц кварца, проходящих через фронт пламени. |
Кварцевые пылинки, оаавлявшие характерные треки, видные на Лотоїрафии. Как следует из снимка и приведенного расчета, значение скорости после фронта пламени заметно Св полтора два раза) больше, чем до него. Это также качественно сходится с расчетом.



 13 августа, 2012
13 августа, 2012  admin
admin 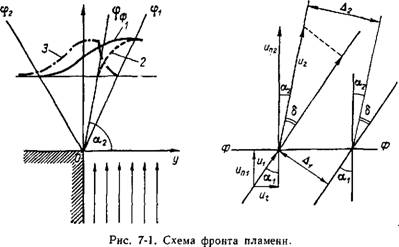
 Опубликовано в рубрике
Опубликовано в рубрике