Как и в других случаях [Л. 21 ], исследование уравнений теплового режима приводит к возможности существования двух типов процесса—гиетерезиеного (с воспламенением и потуханием) и плавного— бескризисного. Последний, однако, близок к кинетическому горению в объеме факела. Поэтому обсуждение его в рамках квазигетерогенной схемы нецелесообразно.
Рассмотрим более подробно критические, условия воспламенения и потухания. Эти условия определяются касанием кривых фх (6) и ф2 (9) в диаграмме ф 6, т. е. следующей системой уравнений:
Используя (6-21) и — (6-22), выведем соотношение для определения критической полноты сгорания. Дифференцируя выражение (6-21) по б при постоянных параметрах р и т, получаем
Так как і/ ехр f—)=-1—^ [см. выражение (6-21)1,
Д — к v
Соотношению (6-4) можно придать вид
= (6-26)
Из выражения (6-22) с учетом равенства (1 + ($)/& == = ^ (6)/(0 — 6 J находим
4T(») = -Ь (FJ) М в — в^’
Приравняем теперь (Є) = г|)2 (9) и t|>J (6) = ^ (9). Решая эти уравнения относительно г|), получаем выражение, связывающее критическую полноту сгорания с критической температурой:
292
На диаграмме г|?9 (см. рис. 6-2) нанесены также предельные кривые, проходящие через максимальные значения критической полноты сгорания г|>кр макс и через точки, в которых совпадают критические условия воспламенения и потухания г|)в п.
Из равенства dtyKp/$ = 0 вытекает, что
6 29
4—9 Следовательно,
Ф ———————
Ткр. макс
(2 — 0)2
Уравнение кривой, проходящей через точки, в которых совпадают критические условия воспламенения и потухания, определим из условия с/2^! (6)/с/62 = 0 в виде:
Ф =-Lh — 2 46 ~6′ ] = . (6-27)
Тв-п 2 [ (2__________ 0)2 J 2 р’макс V"*"/
Приведем также выражение, связывающее между собой параметры тд к и 6кр. Это позволит проанализировать влияние скорости газового потока, а также константы скорости реакции на значения критической температуры воспламенения и потухания. Приравняв выражения (6-21) и (6-26), получим
|
ФкР=1 — .f„ яТ • (б-2в) |
Предельное значение ткр, соответствующее совпадению воспламенения и потухания, из уравнений (6-21) и (6-27)-запишем в виде
Х = (2-8)>2(49-8*) уГТ / М _ в-п (2 — 9)2— 2 (40 — 92) у в^ ґ [ в J
Так как при прочих равных условиях т к =
= const k, соотноше-
Ния (6-28) и (6-29) могут быть использованы для расчета влияния скорости газового потока и константы скорости реакции в отдельности.
Из рис. 6-8 и 6-9 видно, что изменение скорости газового потока и константы скорости реакции практически не влияет на величину температуры воспламенения. Температура потухания существенно зависит от т „
Д. к
(т. е. от значений U
> во
И k0). При этом увеличение скорости потока U^ ведет к росту температуры потухания 6П, а увеличение константы ke — к снижению значения 6П. Физически это означает, что при горении высокоактивных топлив (большие значения k0) область устойчивого горения значительно расширена. Увеличение же скорости газового потока ведет к сокращению области устойчивого горения, так как срыв процесса происходит в области более высоких температур.
Запишем также зависимость, связывающую критическую температуру с параметрами и 0. Используя (6-26) и (6-22), для
Сравнительно низких температур б 1 получаем
|
/F |
|
I+4l±i |
_4|3 + 21±*)2д(1+1±Л)
(6-30)
Знак минус перед радикалом в этом выражении соответствует воспламенению, знак плюс — потуханию.
Для высококалорийных смесей при ft со выражение (6-30) приобретает более простой вид:
1 ± 1Л _ бв„
‘ Єкр~————— Г—— •
Исходя из этой приближенной формулы, оценим относительный разогрев системы, отвечающий воспламенению. Разложим подкоренное выражение в ряд. Ограничиваясь первыми членами разложения, получаем
0В«0„.+-1-0І или 6°-9" = Ае.
2 — в. — 2 —
Заметим, что аналогичный расчет в пренебрежении изменением плотности дает относительный разогрев при воспламенении 8В » т. е. тот же порядок величины, что и при учете изменения плотности. С качественной стороны полученные результаты аналогичны соотношениям общей теории теплового режима горения. Это относится и к учету теплоотдачи от фронта пламени излучением. Опуская детали расчета, укажем, что дополнение граничного условия (6-3) еще одним членом — потерей тепла излучением — приводит к новым (теплообменным) условиям воспламенения и потухания. Физически это означает, что срыв горения возможен как при очень малых значениях скорости потока (большие тд к), когда роль теплоотдачи велика, так и при интенсификации процесса по скорости, когда процесс при условиях, близких к адиабатным, переходит из диффузионной области в кинетическую. Подробнее об этом изложено в работе [Л. 21 ].
Все приведенные выше соотношения относились к простому случаю реакции первого порядка. С практической стороны больший интерес представляет газовая реакция второго порядка. Соответствующие преобразования уравнений в этом случае весьма громоздки и могут быть, видимо, оправданы только при конкретных вычислениях. С качественной стороны результаты для реакций первого и второго порядков совпадают, с количественной стороны они отличаются сравнительно мало. Поэтому расчет для реакции первого порядка может служить первым приближением и для более общего случая. Физическое объяснение этой близости. связано
с определяющей ролью нелинейной экспоненциальной температурной зависимости константы скорости реакции.
Для подтверждения приведем краткое сопоставление некоторых формул и результатов расчета для случаев п = 1 и п = 2 без учета изменения плотности.
Выражение для скорости реакции входит в одно только уравнение материального баланса, составленное для поверхности фронта пламени. Поэтому задача сводится к исследованию этого уравнения.
|
RT |
Для реакции второго порядка уравнение (6-19) принимает вид
2D lerf(^)]/ (с — сЛ = V, ехР 1 — erf Орф /57) U ФЧ
Или после преобразований
Ехр
|
+ 1= 0. |
|
1 + |
|
/ |
Из решения этого уравнения получаем
|
Ехр |
|
1 + |
|
-1, (6-31) |
|
1 + |
1
Ехр
Фі =
Д к
Причем выражение для тд к имеет вид
|
Д. к |
. (1 — и (тфУ<)}2}ас«.+Л1+etr (ТФУ’,)].
|
Рис. 6-10. Зависимость ^ (0) для первого (1) и второго (2) порядков реакций. |
[erf {Чуїт)ї ku„kQ.2
На рис. 6-10 для значения тд к= 8 нанесены две кривые, рассчитанные для реакций первого и второго порядков. Из графика видно, что кривые тепловыделения для реакций первого и второго порядков как с учетом изменения плотности, так и при р = = const аналогичны и сравнительно близки друг к другу. При — прочих равных условиях кривые (6) для реакций второго порядка располагаются несколько ниже соответствующих кривых для реакций иервого порядка. Так как выражение ф2 (Щ не зависит от порядка реакции, а стационарные значения температуры и полноты сгорания определяются равенством ifj — ф2, очевидно, что при одинаковых начальных условиях температура (полнота сгорания) для
реакций первого "порядка будет незначительно выше, чем для реакций второго порядка. Этот результат относится и к расчету критических состояний.
Подведем краткие итоги. Сочетание предположения о протекании реакций горения с конечной скоростью на фронте пламени с уравнениями переноса без источников, как и в схеме с бесконечной скоростью реакций, привело к замкнутой краевой задаче. Из ее решения находятся местоположение фронта пламени, значения температуры и полноты сгорания на нем, а также профили скорости, ри2, температуры и концентраций во всей области смешения. По поводу профилей следует указать, что практический смысл имеют два решения — в области высокой, близкой к единице, полноты сгорания и в области практического отсутствия горения. Для первого из них хорошим приближением служит расчет профилей в предположении бесконечной скорости реакций, для второго — расчет смешения газов при отсутствии горения. Таким образом, основной смысл учета конечной скорости реакций состоит в установлении области существования стабильного режима горения диффузионного факела и условий его срыва.



 13 августа, 2012
13 августа, 2012  admin
admin 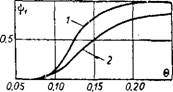
 Опубликовано в рубрике
Опубликовано в рубрике