Для расчета турбулентного диффузионного факела могут в принципе применяться любые расчетные методы, развитые в теории турбулентных струй [Л. 1; 22]. Все они основаны на так называемых полуэмпирических теориях турбулентности [Л. 94 и др. ]. Поэтому от аналитически замкнутого расчета ламинарных струй и факела (см. § 1-2) их отличает необходимость введения некоторой эмпирической информации, заимствованной из эксперимента. В простейших случаях автомодельных течений речь идет об одной — двух опытных константах, в сложных случаях объем сведений, необходимых для создания замкнутой системы расчета и возможности сопоставления с опытом, неизбежно возрастает.
Для автомодельных струйных течений несжимаемой жидкости с примерно равным успехом используются расчеты по теории свободного асимптотического пограничного слоя или слоя конечной толщины, а также методы расчета, основанные на интегральных соотношениях. Широко распространен расчет струй и факела, развитый Г. Н. Абрамовичем [Л. 1 ], на основе априорно принятого профиля скорости и др. Большинство из этих методов расчета неприменимы прямо к неавтомодельным течениям. Достаточной ясности нет также и в вопросе об обобщении известных формул Л. Прандтля для турбулентного трения (теория пути смешения) на движение сжимаемого газа.
Для расчета газового факела большое значение имеет возможность учета непрерывной деформации профилей скорости, температуры и концентрации, а также переменного поля плотности. Этому требованию в известной мере удовлетворяет расчет газовых струй и факела по методу эквивалентной задачи теории теплопроводности. Поскольку в дальнейшем изложении преимущественно используется этот метод, целесообразно кратко напомнить его особенности. Читатель, знакомый с ним, может пропустить последующее изложение, взяв из данного параграфа только справочные сведения (обозначения, применение таблиц и т. п.).
Метод эквивалентной задачи представляет собой, по-видимому, наиболее четкую и наименее обременительную в отношении физических и математических допущений форму использования для расчетных целей давно обратившей на себя внимание схожести кривых распределения скорости (импульса) в поле течения турбулентных струй и температуры в задачах нестационарной теплопроводности. Сравним, например, распространение круглой струи с охлаждением нагретого относительно остального тела цилиндрического слоя. Пусть в обоих случаях начальное распределение будет однородным и граничные условия будут подобными. По длине струи будет происходить постепенное выравнивание импульса, профиль его, постепенно деформируясь, будет все более размываться, т. е. охватывать все более широкую область при непрерывно падающем уровне на оси. На некотором удалении от устья поперечные распределения будут хорошо аппроксимироваться формулой вида и ~ ехр (— у^/а^2). Аналогичное будет наблюдаться и при охлаждении цилиндрического слоя, причем роль координаты к перейдет ко времени (поперечные координаты будут качественно тождественны). Через некоторое время, как показывает аналитическое решение, температурные кривые будут подчиняться той же формуле Т ~ ехр (— #2/а2*)> где а2, как и ранее ах,— постоянная.
Из этой, на первый взгляд, внешней аналогии между процессами рассеяния импульса в турбулентных струях и теплопроводности (или диффузии) следует в принципе возможность, при соответствующих условиях, совмещения относительных кривых распределения, т. е. в конечном счете использования результатов решения одной задачи (теплопроводности) для расчета закономерностей, присущих другой (распространению турбулентных струй). Основным здесь является то, что решение этих разных в сущности физических задач (относящихся, однако, к одному типу процесса — выравниванию начальной неравномерности путем переноса тех или иных субстанций) сопряжено с преодолением качественно различных математических трудностей. В то время как задача о струе относится к числу нелинейных (к тому же выражения для турбулентного трения в уравнениях свободного пограничного слоя в общем случае неизвестны), задача об охлаждении линейна и методы ее решения хорошо разработаны.
Отвлекаясь от различных попыток использования указанного сходства задач и сведения более сложной задачи к более простой, покажем, как реализуется это сходство в методе эквивалентной задачи.
Предположим, что для задач теории турбулентных струй и факела в принципе можно указать такие формулы преобразования независимых переменных, т. е. координат, которые позволили бы описать рассеяние импульса (также избыточной энтальпии и др.) в эффективном пространстве |—г) простейшим уравнением типа теплопроводности и его решениями. Эти преобразования | =’ § (дс, у) и г) = г) (х, у) в каждом конкретном случае имеют определенный вид, который должен быть установлен из опыта.
Прежде чем проиллюстрировать эти соображения примером расчета струи (и факела — в § 3-3), введем одно важное ограничение.
Для многих задач — и только к таким будет применяться метод эквивалентной задачи в этой книге,— как показывает опыт, с практической точностью достаточно применения простейшего вида преобразования координат, а именно — замены § = £ (дс) и г) и у. Иначе говоря, условной деформации («растяжению» и «сжатию» ) для многих задач следует подвергать только продольную координату, оставляя поперечную инвариантной. В этом случае из опыта берется только уравнение связи | (х), зачастую в виде = «= Сх3, и оно представляет собой ту эмпирическую информацию, которая упоминалась в начале параграфа.
Таким образом, говоря далее о методе эквивалентной задачи, будем иметь в виду всегда только этот простейший и экспериментально проверенный частный случай (т) и у). Конечно, он далеко не универсален и неприменим, в частности, к течениям типа полуограниченных струй или рассмотренным в четвертой главе кольцевым струям и факелу. Следует также заметить, что метод ограничен также в отношении формы начального профиля скорости, температуры и концентрации требованием сравнительной гладкости начального распределения и его однотипности (т. е. возможности отнесения к затопленной струе или к спутным течениям, но не к обоим сразу). Содержание этого замечания станет яснее из последующего изложения (см. главу четвертую).
Допустим, что путем простого, заимствованного из опыта преобразования | = § (дс) и г) и у исходная система уравнений (переноса импульса, тепла и вещества в турбулентном свободном пограничном слое сжимаемого газа) заменяется системой линейных однородных уравнений типа уравнения теплопроводности в его канонической форме.
Эти уравнения вида
DF{ _ 1 d I k dFt ~ Ук ду [У ду
Относятся к трем величинам (переносимым субстанциям) — плотности потока избыточного импульса Fu — ри (и — и^), избыточной энтальпии F = = р иср (Т — TJ) и вещества Fg — р и (с — сте), входящим в условия сохранения. В соответствии с этим эффективные координаты (х) имеют в общем случае разные значения: и — для переноса импульса, тепла и вещества. Практически из опыта по изменению рыДы по оси струи заимствуется только зависимость |и = §„(*)• Две другие приведенные координаты |q и как показывает опыт, в подавляющем большинстве случаев струйных течений можно принять равными |u = const и = gg. Значение постоянной а, равной отношению а = J%,q, сравнительно мало меняется (а « 0,7 0,85). Ориентировочно для струй можно принять а « 0,75.
Для упрощения обозначений в дальнейшем везде индекс и отброшен, т. е. обозначено F = Fu, % = а также | = а|? =
Уравнения (1-26) подлежат интегрированию взамен системы уравнений свободного турбулентного пограничного слоя сжимаемого газа, которые могут быть сведены к виду (1-26) при соответствующем выборе выражений для турбулентных напряжения трения и потоков тепла и вещества [JL 22].
Заметим, что уравнения (1-26), в частности первое Из них —динамическое, не содержат поперечного компонента скорости v. Для его приближенного определения следует использовать, как и обычно, уравнение неразрывности
Д, в (1-26)
P„ = __L. Af^V
Uk дх дх
Преимущество метода эквивалентной задачи состоит, во-первых, в применимости его не только к автомодельным (при одной эмпирической константе С в формуле j/Ј~ = Сх), но и к неавтомодельным струйным течениям и, во — вторых, в применимости его к течениям сжимаемого газа, т. е. к тем практически важным случаям, когда выражения для тт, qT, gT неизвестны. Эти обстоятельства делают метод удобным для приближенного расчета факела. Вместе с тем использование его для расчета факела имеет свою спе^ цифику.
Как указывалось, зависимости (х) при расчете газовых струй заимствуются раздельно из опыта путем сравнения теоретических и эксперимен
тальных кривых изменения ри (и — uj) и ри (Т— TJ) по оси струи.[6] Такое сравнение дает две формулы связи приведенных координат с реальными:
І = I (ж) и q = і, (х).
В факеле измеряются величины рн2 и температура. По ним рассчитывается и сопоставляется с решением одиа только зависимость — изменение ри (и — «„) по оси. Это дает одну координату £ = їи(х). Вторую координату (£? = £й или константу а в выражении £ я ot, q) следовало бы определить из сопоставления эксперимента (температурное поле факела) с расчетом для разных значений о. Однако такой путь сравнительно несложен только для автомодельных решений. Расчет иеавтомодельных течений в полном объеме (при а ф 1) весьма сложен. Поэтому в качестве известного приближения может служить расчет, выполненный для случая а — 1.
По-видимому, метод может успешно применяться и к трехмерным течениям (струя и факел, истекающие из прямоугольного насадка) и для ориентировочного расчета течений при наличии градяента давления — закрытых факелов и слабозакручениых струй (при этом Fu = риг + р). Последнее требует, однако, специального исследования.
Для струйных течений эффективность сведения уравнений свободного турбулентного пограничного слоя сжимаемого газа к уравнениям типа теплопроводности подтверждена сравнительно обширным экспериментальным материалом [Л. 7; 8; 22; 23; 63].
С математической стороны линеаризация уравнений существенно упрощает решение задачи и позволяет во многих случаях довести расчет до конечного вида. Действительно, методы интегрирования однородного уравнения теплопроводности подробно разработаны в математической физике [Л. 85]. При этом решение осесимметричиых задач теории теплопроводности для безграничных областей выражается обычно в виде так называемых Р-функций:
Уо
Р (Є, „> = J — ехр (- jjj.) j ехр (- У0 (Ж) р,1.27а)
О
Где р — переменный радиус в плоскости £ = 0 и J о — функция Бесселя первого рода нулевого порядка.
В предельных случаях Р-функция сводится к виду
И
Р(£, у) = -1-ехр(—при 5 > 1.
2Е 45/
Аналогично этому решение плоских задач для безграничной области выражается через интегралы Гаусса:
Ф (6, у) = erf_ erf, — (1-276)
2КЄ 2 У {
|
При є « 1 |
2 z
Где erf (?) = —— Г ехр (— t2) dt — интеграл Гаусса. , У’к о
Функции Р (I, у) и erf (2), так же как и бесселевы функции, затабули — рованы [Л. 102; 11], что существенно упрощает решение. Для удобства расчета таблицы этих функций в необходимом интервале значений аргументов приведены в приложении.[7]
При подобных граничных условиях решения осесимметричной и плоской задач теории теплопроводности [уравнения (1-26) для безграничных областей ] могут быть представлены единообразно в виде частных интегралов — функций Р у) или Ф у) соответственно. Удобно поэтому ввести единое для них обозначение — функцию L (g, у), сократив тем самым изложение общей для обеих задач части решения.
Покажем это на примере решения задачи о распространении турбулентной неизотермической газовой струи в спутном однородном потоке. Как будет видно из дальнейшего, решения аналогичных задач теории факела во многом схожи с приводимым примером, который может поэтому служить своего рода кратким введением к более сложным задачам.
Схема течения и основные обозначения указаны на рис. 1-8. Предполагается, что струя газа (со скоростью но, температурой То и плотностью ро) истекает из круглого или плоского сопла размером уо (t/o — радиус или полуширина выходного сечения сопла) в неограниченный однородный спутный поток, движущийся параллельно струе (со скоростью н^, температурой Т^ и плотностью газа р^).
Решение методом эквивалентной задачя теории теплопроводности сводится к интегрированию уравнений (1-26) для переноса импульса и тепла, т. е. для функций
|
Рис. 1-8. Схема газовой струи в |
|
Распространения спутном потоке. |
|
Р«Мг-г-) WPo(To-T~)’ |
. . , . . …, Т
|
Fq = |
Fu ———————- — и
Ри (н —
При следующих граничных условиях (в координатах £ = У = У/Уо)’
|
F„=l, Fq= Fu = 0, = 0 = 0 |
|
При 0 < у < 1, При 1 < у < оо При у = 0, при у = оо. |
|
При fy > 0 |
|
DFu _ dFq |
|
(1-28) |
|
При & > 0 |
|
Fu = |
|
F<i = 0 |
Решение уравнений (1-26) можно представить в виде
Fu = Аи + BUL (£„, у), Fq = А„ + BqL (f?, у),
Где L і/) = Я. (І, і/) — для осесимметричиой (k = 1) и Z, у) = Ф у) — для плоской (ft = 0) задачи.
Из граничных условий (1-28) следует Л; = 0, В,- = 1, так что решение для обеих задач записывается так:
Ft = Hb. y) (1-29)
Или в расшифрованном виде
Ро"о("о-°») Ро"осРо(Го-Г») И /
Где обозначено | = Јu =
Таким образом, распределение величин риАи и рисрАТ в пространстве £, у найдено. Для расчета первичных характеристик течения — скорости, температуры и плотности — приходится пренебречь различием между осред — ненным в смысле Рейнольдса значением произведения двух (или более) величин н произведением их средних (в том_же смысле) значений. Иначе говоря, следует положить, например, ри — р-н; ри2 = р-и2 и т. д.
В этом предположении [8] уравнения (1-30) позволяют выполнить несложный алгебраический пересчет и найти в конечном итоге распределение всех переменных в пространстве, занятом струей. Не приводя деталей, укажем на ход расчета, а затем приведем конечные выражения.
Введем обозначения m = и^/ид и ш = р„/р0 = TQ/Tж. Примем для простоты ср « const. С учетом этого уравнения (1-30) перепишем в виде
JfL/JL-^O-^ME. у), (р")о V"»
Р" -»JL = (i_e)i(_i_t!,
(р")о "»
Эти выражения (с учетом равенства р/ро = TulT) представляют собой два уравнения с двумя неизвестными u/ua и ри/(ри)о. Решая их совместно, приходим к квадратному уравнению относительно величины «/«о:
|
, 1 , / є « + —— Ч — |
|
— + —— — mL (— , у |
|
И "о |
L (5, у) = 0.
Решение этого уравнения дает распределение скорости течения и, следовательно, всех остальных переменных во всем поле струи. Конечные выражения для краткости сведем в таблицы: табл. 1-1 относится к частному случаю затопленной струи (и= 0, m = 0); табл. 1-2 — к общему случаю спутной струи.
Таблица 1-1
Выражение
|
Г |
|
*■> У) |
|
V |
|
1 + |
|
= /і(І ± /а) |
2ш lL ‘ У
[•»Л(-1 +/»)J~ ‘ L — І-, у
Таблица 1-2
Выражение
|
2 2а |
|
=/ |
|
Н-‘): |
|
1 — ш 2ш |
•(Л ±/«)-/.. = . г/|
Ll-~, у)[<о (/3 ± /4) —Л]
В формулах табл. 1-1 и 1-2 выражения вспомогательных функций Д—/4 видны из первых формул; знак плюс перед корнем (или функцией /4) отвечает значению a) > 1 и знак минус — значению w < 1. Напомним, что для осесимметричной задачи L у) н Р (£, у) и для оси струи (при у = 0)
|
—і |
/>(6, 0) = 1-е*р (1-31)
Аналогично этому для плоской струи
|
1 |
|
(1-32) |
|
2V( |
L (5, 0) е Ф (Є, 0) = 2 erf
Выражения, сведенные в табл. 1-1 и 1-2, определяют распределение всех переменных в приведенном пространстве. Установив из опыта связь координат £ = £ (х), а также a = g/Ј?, нетрудно перейти к распределению переменных в пространстве х, у. Тем самым расчет доводится до конца (подробнее см. [Л. 22]). Полученные формулы будут использованы в примере расчета в § 3-3.



 13 августа, 2012
13 августа, 2012  admin
admin 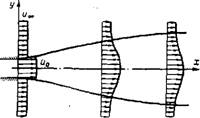
 Опубликовано в рубрике
Опубликовано в рубрике