Принято различать две формы прямоструйного факела — затопленный факел и спутный. В первом случае речь идет об истечении, струи топлива в пространство, заполненное неподвижным окислителем (например, воздухом), во втором — об истечении струи топлива в движущийся параллельно спутный поток окислителя. Второй случай, очевидно, является общим и содержит в себе в качестве
Частного, при равенстве нулю скорости спутного потока, задачу о затопленном факеле. Поэтому для общности, говоря о диффузионном факеле, будем иметь в виду спутный факел, схематически представляя его следующим образом.
Допустим, что струя горючего газа (топлива) вытекает из круглой или плоской горелки в спутный поток окислителя. Распределения скорости в выходном сечении сопла и спутаем потоке, так же как начальное (при х = 0) распределение температуры и концентрации топлива и окислителя, будем считать заданными. Для простоты примем их, как показано на рис.-2-1, равномерными.
При истечении газа из профилированного сопла строго по направлению оси х, при параллельности спутного потока и струи давление во всем пространстве, занятом факелом, можно считать постоянным. Если вблизи устья горелки установлено стабилизирующее устройство (например, тонкий кольцевой стабилизатор, размерами которого и влиянием на течение можно пренебречь), то в турбулентном пограничном слое — области смешения, образованной параллельными потоками топлива и окислителя,— установится устойчивый стационарный фронт пламени. Фронт этот начнется вблизи кромок сопла (точнее — у стабилизатора). Вначале он несколько расширится, а затем на сравнительно большом расстоянии (порядка десятков и более калибров) сузится и, наконец, сомкнётся на оси факела.
|
Рис. 2-1. Схема диффузионного факела конечного размера. |
В предположении о бесконечно большой скорости химической реакции горения, общем для этой части книги, фронт пламени можно представить в виде поверхности, в основной своей части близкой к цилиндрической, разграничивающей факел на две области. Одна из них — внутренняя зона I (см. рис. 2-1) — заполнена топливом и продуктами сгорания, вторая — внешняя зона II — окислителем и продуктами сгорания. К поверхности фронта изнутри диф
фундирует топливо, извне — окислитель. От фронта пламени в обе стороны — во внутреннюю и наружную зоны факела — диффундируют продукты сгорания. На самом фронте концентрация каждого из реагентов равна нулю, а концентрация продуктов сгорания максимальна. При этом притекающие к фронту и сгорающие на нем диффузионные потоки реагирующих газов — топлива и окислителя — находятся в стехиометрическом соотношении.
С качественной стороны распределение температуры (максимум на фронте) и концентраций реагентов вблизи фронта пламени, а также распределение скорости в турбулентном факеле аналогичны распределению этих величин при ламинарном диффузионном горении (см. § 1-2). Поэтому рассмотренная картина диффузионного факела относится как к турбулентному, так и к ламинарному факелу конечного размера (спутному в общем случае или затопленному — в частном).
Строгий количественный расчет диффузионного факела конечного размера крайне сложен. Однако именно эта (неавтомодельная) задача представляет наибольший практический интерес; ей же свойственны наибольшие трудности вычислительного характера.
Математическая постановка рассматриваемой задачи в общем случае сводится к следующему. Совместному интегрированию подлежит система нелинейных дифференциальных уравнений в частных производных для стационарного осесимметричного (k = 1) или плоского (k = 0) турбулентного или ламинарного пограничного слоя сжимаемого газа.
Для турбулентного слоя выражения т = хт, q = qr и g = gT (для турбулентных касательного напряжения трения и потоков тепла и вещества), стоящие справа в написанных ниже уравнениях переноса, должны быть раскрыты с помощью одной из полуэмпирических моделей. Как правило, все они включают в себя производные (скорости, температуры и др.) по координате у, так что уравнения будут второго порядка по у и. первого — по х. Для ла-
Т ду q дТ g
Минарного слоя, когда —=>—. — =—^— и = v Р ду ?сР ду Р
Дс
= — D—- — по законам Ньютона, Фурье и Фика, этот порядок ду
Дифференциальных уравнений очевиден.
К системе уравнений, о которых идет речь, относятся следующие:
|
|
|
У-тУ{укх)> |
|
|
|
:= 0, рГ = const, Ду |
|
,ж дТ, _ _L А (у*?) = J_ Д (у*?) Ду у" ду |
Объединяя первое из этих уравнений со вторым (уравнением неразрывности), его часто переписывают в виде
Д? и (u Uqq) dy"pv (и — и^) _ д (укт)
Дх Ук ‘ ду ~~ ук ‘ ду
Для спутного течения (и^ — скорость в невозмущенном спутном потоке) или при их = О
|
Dykpuv Ду |
|
1 д (<Л) |
|
Зри2 дх |
|
+ Л— У |
|
Ду |
Аналогично этому уравнениям энергии и диффузии придают вид уравнения сохранения:
1 D(yk 9vcp^j) _ J_
Ду
1 д (ук pvb. cs)
+
Ду г
Отсчитывая температуру и концентрацию от некоторого постоянного значения (например, на фронте пламени или в невозмущенном спутном потоке).
Возвращаясь к системе уравнений (2-1), замечаем, что третье уравнение в ней (уравнение состояния идеального газа) написано в простейшем для расчета предположении, что молекулярные веса газов (топлива, окислителя и продуктов сгорания) близки между собой, так что влияние их на плотность смеси газов не учитывается.
Индекс / в уравнении энергии может иметь два значения: I и // — соответственно двум зонам факела —внутренней и внешней. Наконец, индекс s в уравнении диффузии, как и ранее, может иметь три значения: s = а, б, в — соответственно топливу, окислителю и продуктам сгорания (принципиально в каждой из зон / и //; в действительности в зоне I будет s = а, в, а в зоне II, в свою очередь, S = б, в).
|
Д (рисрАТ,) дх Д(р иДс5) дх |
|
Ш |
|
+ ЛГ У |
|
У |
Выпишем теперь граничные условия для системы уравнений (2-1):
О < У < Уо, и=и0, Т — Т0, са = сао, св = О, у0<У< + со> и = иоо, 7 = Г.,
Б О, +0О ‘ 8 ‘
А) 0<У<Уф~в зоне I
Ди __ дТ ___ дса
Ду ду ду т = Тф, са = 0, св = Сдф при у = I/ф;
Б) — в зоне II
Т = Тф, сб = 0, се = свф при у = уф, и = и«. Т = Т„, св = се>„;
|
При х = О |
|
О при у = О, |
|
(2-2) |
|
При *> О |
В) се = 0 при У — оо.
Кроме того, на поверхности фронта пламени, т. е. при і/ф = = у (л:ф), соблюдается сформулированное ранее стехиометриче — ское условие для притекающих к фронту потоков реагентов:
|
|
Поскольку уравнения пограничного слоя относятся к параболическим дифференциальным уравнениям (в которых пространственная координата х играет роль как бы «времени» в уравнении типа теплопроводности), задача в целом в связи с условием на фронте относится к классу краевых задач с «движущейся границей» Уі> = У (хф)• Классический пример задач такого рода — известная задача Стефана о движении фронта плавления и т. п. [Л. 85].
|
F = |
В расчете диффузионного факела уравнение границы і/ф (дгф), как правило, заранее неизвестно и должно быть найдено в ходе решения с помощью соотношения (1-7) или из другого дополнительного условия. Это обстоятельство порождает дополнительную нелинейность задачи, связанную с наличием «движущейся границы». В таком виде решение может быть в принципе получено численно на ЭВМ для конкретных значений параметров. Для турбулентного факела (как и при расчете турбулентных газовых струй) задача усложняется необходимостью ■ задания неизвестных в общем виде выражений для величин хт, qT и gT. В этом случае целесообразно выполнить расчет по методу эквивалентной задачи теории теплопроводности (см. § 1-4), при котором уравнения (2-1) заменяются линейными:
|
|
В уравнениях (2-3) черта сверху означает переход к безразмерным (относительным) величинам. Индекс і при координате h и функции Ft соответствует и, q и g, причем, как отмечалось в § 1-4, У ІиИ Fи индекс и в дальнейшем будет отброшен (£ F = Fu). Безразмерные величины Ft примем в виде: для всей области течения
Ри (ц — ы^)
Роио("о-ц~) ‘
Для внутренней / (для топлива) и внешней II (для продуктов сгорания) зон факела
|
Р »ср(Т~Т~) ■ |
|
И F |
|
Р„«ЛФ(гФ-Г-) ‘ |
|
«II |
Р = Риср (Т — 7ф) И Ч! Ft«h-o (то — Тф)
|
Р исв РфИфСцф |
PUCq
Р __ рта &а роиосао ‘
Кроме того, обозначим: g. =|;/iи у = і/Л/0 — безразмерные координаты, если у0 — характерный размер (радиус или полуширина) выходного сечения сопла горелки. Разумеется, что выбор масштабов для безразмерных функций Ft и начала отсчета для них произволен; принятый выше удобен тем, что сокращает преобразования в ходе решения. Для упрощения записи в дальнейшем черта над безразмерными величинами, а также индексы q и g у F,, Fga и т. д. будут отброшены. Это не может привести к недоразумениям, поскольку эти величины относятся в расчете к разным зонам факела. Последнее видно из граничных условий к системе (2-3), записанных в виде:
О <У<У0, F, = l, Fa = l,
Уо<У<+°°’ 0. Fu = 0, Fe = о.
А) 0 у < уф — в зоне / dF_ = .dFi _ д£а_ ду ду ду Fi = ]> ^ =0 при у= уф
Б) Уф < У < оо — в зоне /I ^П = l> F,= l При У = Уф> F — 0, Fп — 0, Fe — 0 при у — со.
Кроме того, для границы, которая разделяет зоны и на которой Уф = Уф(Хф), сохраняется условие (1-7), необходимое для отыскания уравнения фронта пламени.
В таком виде краевая задача распадается на две. Независимо от других уравнений интегрируется уравнение для функции F, определяющее непрерывное во всей области течения (для самой функции и ее производных по координатам) распределение избыточной плотности потока импульса риЛи. Это отделение динамической задачи весьма важно, так как делает возможным самостоятельное сопоставление решения с экспериментальным полем ри2 и определение (по падению ри2 на оси факела) связи приведенной координаты £ = £ (*) с реальной координатой х.
|
При Е = О |
|
О при у — О, |
|
(2-4) |
|
При I > О |
В отличие от этого, уравнения переноса энергии и вещества должны интегрироваться для определения функций Fq и Fg раздельно по зонам факела. Хотя сами функции (или, более точно, отвечающие им физические переменные: температура и др.) непрерывны, производные их терпят разрыв на фронте. В зоне I при выбранной схеме решения должны интегрироваться уравнения для функций Fl и Fa, в зоне II — для Z7,, и Fe. Этого достаточно для определения концентраций всех газов (а, б и в) во всем поле, поскольку в зоне /, очевидно, с6 = 0, а в зоне II, соответственно, С„ = 0.
Несмотря на линеаризацию уравнений при переходе от системы (2-1) к системе (2-3), задача остается все же нелинейной из-за наличия в ней «движущейся границы» — поверхности фронта пламени. Дополнительная трудность связана еще и с тем, что условие (1-7) формулируется не относительно одной из функций Fq или Fg, а относительно концентрации cs. Это приводит к взаимосвязи всех трех уравнений для функций Ft. Результаты совместного решения их следует использовать для перехода от распределения сложных величин ри (и — «J, ри (Т — и т. д. к распределению первичных — температуры, скорости и концентрации. И лишь после этого можно удовлетворить условию (1-7) и тем самым отыскать местоположение фронта пламени и замкнуть задачу в целом.
Аналитическое решение такой задачи не содержит принципиальных трудностей в том случае, когда приведенные координаты^ совпадают, значение и переход к физической плоскости те
Чения для всех функций F{ одинаков. При этом фронт пламени, на котором Т = Тф = const и саф = сйф = 0, будет не только изотермической поверхностью, но и, с учетом равенства рТ = const, поверхностью постоянного значения скорости, плотности тока, динамического давления и вообще любой функции Ft. То же самое относится к каждой «изоповерхности» в эффективном (g, у) или реальном (х, у) пространстве. В физическом плане это сводит задачу к идеализированной, отвечающей расчету при равенстве единице своего рода турбулентного числа Прандтля. Как будет показано ниже, решение такой задачи отражает все важнейшие свойства реального факела. Это обстоятельство определяет целесообразность использования такого приближенного (в физическом отношении) решения задачи о факеле конечного размера. При этом, естественно, игнорируется хорошо известное из экспериментальных данных по турбулентным газовым струям [Л. 22] и несомненно присущее факелу различие в интенсивности переноса импульса и тепла (неравенство а < 1, если £ = o%q).
Как будет показано в следующей главе при сопоставлении результатов расчета с экспериментом, решение в предположении а ж 1 правильно отражает главные закономерности диффузионного факела и может служить основой для приближенного количественного расчета. Правда, во всех обработанных опытах (см. § 3-1) заметно систематическое отклонение опытных данных от расчетных (для случая а = 1), которое является следствием того, что и в факеле при а < 1 перенос тепла происходит несколько быстрее переноса количества движения, профили температуры в поперечных сечениях факела, как и струй, несколько шире профилей скорости, расчетная длина факела (при а=1) меньше экспериментальной. Остается открытой поэтому возможность в последующем численного решения краевой задачи во всей ее сложности, т. е. с учетом различия приведенных координат^.
Общий метод решения таких задач теории теплопроводности изложен в руководствах по математической физике [Л. 85].
Получение его связано с большим объемом вычислений с помощью ЭВМ, в частности, из-за неизбежности применения в ходе решения последовательных приближений при отыскании координат фронта. Такой расчет, проведенный для конкретных значений параметров, хотя и потребовал бы для обобщения и сопоставления с опытом значительной вариации расчетных условий, позволил бы в принципе выявить из эксперимента [9] наиболее отвечающее ему значение а. Выполнение такого рода численных расчетов, вероятно, окажется целесообразным при дальнейшем накоплении и уточнении экспериментальных данных.
В последующем ограничимся изложением приближенного решения задачи для случая £=£?=£в, т. е. <т=1. Результаты этого решения (см. § 2-3) будут позднее (в § 3-1 и 3-2) сопоставлены с экспериментом.
Целесообразно, однако, предварительно привести решение более простой (автомодельной) задачи о плоском турбулентном фронте пламени, расположенном в зоне смешения двух плоскопараллельных спутных потоков. Для этой задачи, аналогичной рассмотренной в § 1-2 для ламинарного диффузионного факела, закон «движущейся границы» определяется сразу из соображений размерности:
Уф — (при J/ffc = Сх, очевидно, уф — хф, поверхность фронта дает В пересечении С ПЛОСКОСТЬЮ Х — у прямую уІХф = const). В этом случае линии постоянных значений функций Ft, температуры, скорости и концентрации совпадают с приведенными координатами
^ = у / y^r. — const. Поэтому решение автомодельной задачи (см. § 2-2) доводится до конца при произвольном значении а. Результаты решения позволяют оценить влияние выбора значения о на местоположение фронта пламени и структуру факела.



 13 августа, 2012
13 августа, 2012  admin
admin 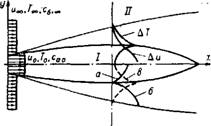
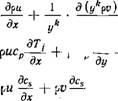
 Опубликовано в рубрике
Опубликовано в рубрике