В качестве вводной теоретической задачи рассмотрим ламинарное горение предварительно не перемешанных газов в свободном пограничном слое, образованном при смешении двух плоскопараллельных потоков топлива и окислителя [Л. 43].
Как и в других случаях, результаты исследования ламинарного факела, опирающиеся на физически строгие уравнения, свободные от введения эмпирических данных, служат качественной моделью расчета турбулентного диффузионного факела. Более того, физи
ческая схема явления, общая постановка задачи, граничные условия, метод решения — все это в известных пределах одинаково для ламинарного и турбулентного факела. Поэтому для рассматриваемой ниже задачи выпишем подробно систему необходимых уравнений, граничных условий и все основные преобразования. Наряду с этим оговорим принятые допущения с тем, чтобы в дальнейшем, как правило, не повторять этого.
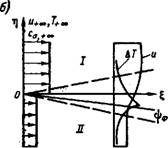
Схема течения показана на рис. 1-2. Примем, что по обе стороны полубесконечной пластины движутся без трения однородные потоки реагирующих газов, приводящие в соприкосновение в точке О (начало координат на рис. 1-2, а). Начиная от этой точки
Образуется область смешения — свободный пограничный слой, «)
Рис. 1-2, Схема плоскопараллельного пограничного слоя при горении неперемешанных газов: а — плоскость физических координат х, у; б — плоскость переменных 5, ї)-
Внутри которого располагается диффузионный фронт пламени. Стабильность его обеспечивается поджиганием по линии х — О, у = 0. Скорости химических реакций горения будем считать бесконечно большими и в соответствии с этим зону горения — поверхностью фронта пламени. Тем самым принимаем, что во всем объеме, занятом факелом, реакции горения отсутствуют. Реагирующие газы поступают с обеих сторон к фронту и мгновенно сгорают на нем.
В задачу расчета входит определение местоположения фронта пламени и распределения температуры, скорости течения и концентраций топлива и окислителя, а также продуктов сгорания в любом поперечном сечении факела. Примем также, что течение происходит в поле постоянного давления. Поэтому плотность’ газа будем считать величиной, обратно пропорциональной температуре (рТ = const), не учитывая различия молекулярных весов газов (реагентов и продуктов сгорания). Кроме того, температурную зависимость коэффициентов вязкости, теплопроводности и диффузии примем линейной ([і — X ~ pD — Т), а числа Прандтля и Шмидта — постоянными (Pr = via = const, Sc = v/D = const).
Пренебрежем также изменением молекулярного веса газов и теплоемкости при реакции. Такое допущение приближенно отвечает горению в присутствии достаточно большого количества инертного газа (азот в воздухе и др.). В принятой схеме пространство, занятое факелом, условно разбивается на две зоны, разделенные- фронтом пламени — поверхностью слабого разрыва для температуры и концентрации. На этой поверхности производные температуры и концентрации по координатам терпят разрыв, тогда как сами переменные непрерывны.
В одной из зон (/), расположенных по обе стороны фронта, находятся газы — топливо и продукты сгорания, во второй (//) — окислитель и продукты сгорания. На схеме факела (рис. 1-2) зона I расположена выше фронта пламени, а зона II — ниже.
Систему уравнений стационарного ламинарного пограничного слоя сжимаемого газа запишем в следующем виде: уравнение движения ди
. ди д І ди л i
|
Р" * |
Уравнение неразрывности
^ + ^=0, (1-2) дх ду
Где и и v — компоненты вектора скорости.
Эти два уравнения являются общими для всей области течения, поскольку на фронте пламени отсутствуют источники или стоки импульса и массы. Уравнение энергии
ДТ. дТ д /, дТ ,, „,
РЫСр — + РУСр-==-(Х-), (1-3)
Где ср — теплоемкость. В этом уравнении опущены члены, учитывающие лучистый теплообмен, диффузионную теплопроводность и теплоту трения.
Уравнение диффузии для s-ro компонента смеси (s = а, б, в, причем эти индексы здесь и в дальнейшем относятся соответственно к топливу, окислителю и продуктам сгорания)
В этом уравнении не учтена термодиффузия. Уравнение состояния идеального газа (для случая р = const и ~ йб ~ Iі.)
РТ = const. (1-5)
Уравнения, учитывающие зависимость коэффициентов переноса от температуры:
Уравнения энергии и диффузий — следует интегрировать раздельно для каждой из двух зон І ичМ. і расположенных по разные стороны фронта пламени. В одной из них, как отмечалось, происходит встречная диффузия топлива:« йрбдуктов сгорания, во второй — окислителя и продуктов сгорания.
Граничные условия, при которых следует интегрировать систему уравнений (1-1) — (1-6), имеют вид: для левой полуплоскости (х <; 0)
Ы=ы+00, Т = т+са = са>+„ при#>0, ,
" = "_оо. T = при г/<0;
Для правой полуплоскости (х > 0)
" = "+-. T = T+mt са = са+„ при у = + со,
|
Са б = 0 при у = Уф (х). |
И = , Т = , сб = сб при у = — оо;
На фронте пламени Т = 7
Индекс «ф» указывает, что значение данной величины относится к фронту пламени.
Эта система вместе с граничными условиями может быть проинтегрирована, т. е. может быть найдено распределение профилей скорости, температуры и концентрации во всем поле факела. При этом, однако, в полученные выражения будут входить в качестве неизвестных координаты фронта пламени г/ф и хф, связанные между собой уравнением фронта г/ф = у (лгф).
Для того чтобы довести задачу до конца, т. е. определить местоположение фронта пламени, запишем дополнительное условие, связывающее диффузионные потоки топлива и окислителя на фронте пламени:
= S, ;(1-7)
Где О — стехиометрический коэффициент (отношение масс компонентов при реакции); д/дп — производные по нормали к поверхности фронта пламени. Прямое решение задачи требует совместного интегрирования всех уравнений, .Эффективным приемов решения является переход к переменным, допускающим отделение динамической задачи от тепловой и диффузионной. С этой целью введем преобразование А. А. Дородницына -.[Л. 38] для случая р = const в виде
У
Г= [3]7J =f f
‘ av » б
Выпишем формулы замены переменных:
JL = 3
Дх
Д _ & д дт д
Д
Р— •
Ду ду д£ ду дт ду
|
2v |
|
І=х, у} = Jpdt/, о |
|
А, Дх |
|
Pv + и |
Для сокращения записи введем безразмерные переменные и; параметры:
2 и
И =
, — +
™ Т — Т.
AT.=—————— і
1.11 у ____ у
" + 00 +
С =
Ф
|
M |
|
— ди, — ди и — + дЦ дт{ |
И, L
Ї-f/ Re
І-
(L — произвольный масштаб длины). Поскольку в условия задачи! величина размерности длины не входит (задача автомодельна),, масштаб L в последующем сокращается.
В новых переменных система уравнений (1-1) — (1-4) может быть записана так:
|
Д дг) _ д дг] д Дх д£ дх дгі д; дх ду ‘ |
Д*й o>f ‘
|
Дм |
|
— J_ Д’АГ ~ Рг _L. ^ Sc ‘ d^ ‘ |
|
— дТ И —— Ае И -=- |
|
Л, |
|
(1-8Х |
|
01, |
+ о
Эта система по форме совпадает с системой уравнений ламинарного пограничного слоя несжимаемой жидкости. Граничные условия! в новых переменных имеют вид: для левой полуплоскости (С 0)
И = j-p—, v = 0, Дf, = 0, са = 1 при ~t > 0, ы = 2/" , у = 0, Д7 =0, с, = 1 при у < 0;
I 4- m
Для правой полуплоскости (| > 0)
И = —~—, ДГ, = 0, са = 1 при у] = — Ксо,
1 + «
|
U = |
— 2/л
, &тґ1= 0, 1 .при У) — оо;
1 + m
На фронте пламени
Л^ьп = !> = ° ПРИ 4 = V
Поскольку задача в плоскости переменных г), 1 автомодельна, т. е. допускает переход от уравнений в частных производных к обыкновенным дифференциальным уравнениям, осуществим так называемое преобразование автомодельности. Для этого введем новые переменные:
Ы = F (ф), AT = е (ф), с = «(ф), ф =
(у — константа автомодельности, F’, 9, я — универсальные функции координаты г|з). Из формул замены переменных:
= і.- і і. JL — it JL— FT_Ё_ dl ~ дї ‘ df ~ t Г ‘ ді/ ‘ ОІ^ ~~ dV d|< ~~ ді/ ‘
J^ /г-т 5 <3rja дт)
Найдем
И =
О
ДМ ф Rw/,4 5с ф
От) от]
^-w,». «-Р.-»,
(штрих — дифференцирование по ф).
|
(1-9) |
После подстановки этих выражений в систему уравнений (1-8) приходим к следующим уравнениям:
/■’"(ф)^+1- (ф) F (ф) = О, в"(ф)’Г[+,-тРгв'(ф)^(ф) = 0, * (Ф)?т+1 — Т Sc % (у) F (ф) = 0.
Для независимости полученных уравнений от переменной | положим у = — V2. Тогда ф = ц/ и система (1-9) примет вид
Є"(Ф) + ©’ (Ф) Сф) = 0.
Граничные условия (при £ > 0), при которых следует интегрировать эти уравнения, следующие: 2
В(ф), = 0, «(<[>)„ = 1 при ф = + со, 0(Ф)ц=О, я(Ф)в = 1 при ф = —со,
1 + т
В <Ф)«. и = Ь «(Ф)». в = 0 ПРИ
Решение первого уравнения системы (1-10) выполним, следуя методу итерации, примененному Гертлером [Л. 110] при решении задачи о смешении плоскопараллельных потоков несжимаемой жидкости. Для этого представим искомую функцию F (ф) в виде ряда
|
(1-12) |
^(ф) = 2(т_1)Х(<|>) 0-11)
Л-0
И первый член разложения г0 (ф) примем равным г|з. Используя разложение (1-11), т. е. подставляя в уравнения (1-10) функцию F (ф) и ее производные и приравнивая коэффициенты при одинаковых степенях разности т—1, получаем систему уравнений для определения функций Fn (г|з):
Fl (ф) + 2tyFi (ф) = 0,
F; (ф) ч — 2ф^ (ф) = — 2Л (ф) F (ф),
С граничными условиями
|
F (- °°) = |
Л (+<*>) =
1 + т 1 +т
|
(1-10) |
|
F0» = F(<|») = |
|
1 + т 2т |
F‘n(± оо) = 0 (п> 2).
|
(1-13) |
|
17 |
Ограничимся первым приближением, так как последующие, как известно из решения аналогичных задач, вносят незначительные уточнения. Интегрируя первое уравнение, получаем
F (ф) = Сг | erf (2) dz + С2ф + С8, о
2 Заказ № 2565
Erf(z) =-^L f«r’sd/.
У71 о
Постоянные интегрирования найдем из граничных условий: Сг — — , С2 = 1, С3 = 0.
1 + т
В окончательном виде
F‘ (ф) = И = — і— [(1 + m) + (1 — /п) erf (ф)]. (1-14)
1 + т
Полученное решение совпадает с выражением для скорости в задаче о смешении потоков газа [Л. 22]:
" = JL [(1 + m)+ (!-«) erf (ф)].
"+» 2
Для определения профилей температуры и концентрации проинтегрируем второе и третье уравнения системы (1-10):
Є(ф )=C’l][F(z)]Prdz + C’2, — (1-15)
О
И(ф)=с;|[/ (z)]scdz+c"2. (Мб)
О
Значения постоянных интегрирования определяются из граничных условий и соответственно равны:
Для зоны I (топливо — продукты сгорания)
Сі = — —1= .————— ^—— —— , С2 =
•Vb 1 —erf (фф/Рг) ‘ І-erf (ффТ^Р7)
CI = — —у= •— т~~—. С2= 1;
V Sc l_erf (фф У Sc),
Для зоны II (окислитель — продукты сгорания) с" — 1 1 Ґ — 1
Lq — —= .———————- , 1>2—
V Pr 1 + erf (фф ~V~Pr) ‘ 1 + erf (фф У^Рг)
1 1
С2 = 1.
Vsc і+егі{фф Vst)
В результате получим следующие выражения для функций 9 (-ф), я (ф), описывающих распределение температуры и концентрации в факеле:
ДЛЯ ЗОНЫ / (арф < < + оо)
В, — Т~Т+~ = , (1-17)
Гф 1 — erf (фф Ург )
___ = і————— (Ы8)
L-erf^/sc) для ЗОНЫ U (— со < 1)3 <
В„ = Т~Т— L + Erf^V^) ^ (Ь19)
1 l + erf (фф/рг) ‘
J+EltoS-, (1.20)
Ч— l+erf (фф/Sc)
Используя выражения (1-18) и (1-20) и соотношение (1-7),[4]Получаем выражение, определяющее координату фронта пламени г|)ф,
Erf (фф У’Ц = щ. 0-21)
Где
Са, +оо Da
Р = 2
—> De
Для проведения численных расчетов и анализа влияния отдельных параметров процесса на профили скорости, температуры и концентрации необходимо преобразовіать полученное решение в плоскость физических переменных х, у. Связь между безразмерными переменными ф = — q/Y |j и <р = у/У"х определяется из соотношения
Ф
<р
Р(ф)
Так как профили плотности по обе стороны фронта пламени описываются различными выражениями, то в зависимости от значения т|)ф (т. е. от того, будет ли т|)ф > 0 или т|)ф < 0) выражения, связывающие координаты if и ср, будут различными. Запишем их раздельно для двух случаев местоположения фронта пламени относительно линии if = 0.
В том случае, когда фронт пламени находится в области отрицательных значений обобщенной координаты if, формулы перехода имеют вид: для зоны /
Ф
Ф, = при фф<(ф)< 4 ОО; (1-22)
J MW
Для зоны II
І*
![]()
Гіф
Фф =
. р, (‘« о
В случае, когда фронт располагается в области положительных значений координаты ijj, эти формулы принимают вид: для зоны /
Я>і — Фф +■ пГ ПРИ Фф ^ Ф < + °°> О"24)
|
Фф |
Где
Гіф
РТТсР)
О
Для зоны II
Q>n=»f=JL при — оо<ф<ф. . (1-25)
" J РпОИ ^.^ ф
В этих выражениях р, (if), р,, (if) — профили плотности, которые определяются соотношениями (1-17) и (1-19) и уравнением состояния. Исполыуя выражения для р, (if) и рм (if), приводим соотношения (1-22) — (1-25) к виду, удобному для расчета:
|
— 1 |
|
Ф, = ф + ■ |
|
I —erf (фф Vpt) + |
|
Vk Pr |
{[і — [ф erf (ф j/~Pr) 4-
{Exp (— Ф2 Pr) — 1}
При Фф < Ф < 4- со;
Фи = Фф + (Ф — *ф)
І + erf (фф/Рг) 4 [ф erf (ф ]/Рг) — Фф erf (фф урт) +
+ тЬг{ехр F Pr) ~ ехР (- ^фРг) I ]}}
При — 00 < ф < фф,
|
= Фф" |
|
(В, == |
|
ФФ>0 |
Где
U), — 1
{{і’ф + [і’фЄгГ(ффі/РІ:) +
1 —erf (ффУТ^)
Юп =
+ оо
Ф| =ФФ+.(Ф-Фф)+-
—— , ——— ({(Ф ———-
I-erf (фф У Рг ) фегГ (ф /Р^)-1-фЄгГ(фф/Р?) +
+ уЬг {ЄХР ‘2 РГ) ~ ЄХР **
При Фф < ф < 4- оо;
Ф„ = Ф +———- "’І"’ ~{{ф + [фerf (ф +
14 erf (фф j/pr)
|
Фф<0 |
При — оо < ф < фф,
Где
Фф = Фф + —— {{ф»+ [^erf (фф +
|
У пРг |
|
|
1 + erf (фф V Рг )
{ехр Pr)_|j
Проиллюстрируем полученные решения. Распределение безразмерной скорости и температуры в затопленном ламинарном факеле
(случай т = 0, т. е. = 0) показано на рис. 1-3. Из графика видно, что увеличение температуры горения (т. е. теплотворности газа) приводит к заметной перестройке профилей температуры и скорости. Это связано в первую очередь с изменением местоположения фронта пламени, который с ростом температуры горения смещается к внешней границе пограничного слоя. Последнее, разумеется, вполне естественно, так как при более — д -4 q і, /у высоких значениях температуры
Происходит более интенсивное расширение газов, вызывающее сме — Рис. 1-3. Распределение скорости щение зоны горения во внешнюю и избыточной температуры в ла — область. Аналогичная картина
S|?L°oHHo7Top4eZ Р 4Ро! ™еет МЄС™ И "РИ Г°РеНИИ ТуРбу*
Т = 0). лентного факела.
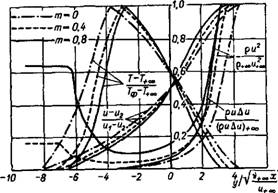
На рис. 1-4 приведены результаты расчета распределения безразмерных значений скорости, температуры, плотности потока импульса ри2, величины ри (и — f и ) в спутном ламинарном факеле. Из графика видно, что изменение параметра т = ы_оо/и+оо вызывает заметную деформацию профилей скорости и температуры. Увеличение параметра т приводит к смещению фронта пламени по направлению к потоку, движущемуся с большей скоростью. Заслуживает внимания своеобразный характер изменения динамического давления в поперечном сечении спутного факела.
Как видно из рис. 1-4, наличие источника тепла (фронта пламени) в зоне смешения приводит к образованию провала в профилях ри2. Профиль избыточной величины ри (и — u_J) остаётся при этом монотонным. Профили температуры в соответствии с принятой схемой расчета имеют острый максимум на фронте пламени. Это является результатом предположения о бесконечно большой скорости реакции. Существенно, что численные расчеты профиля, температуры вблизи максимального значения, выполненные с учетом
конечной скорости реакции, приводят из-за резкой температурной зависимости скорости реакции к практически такому же результату. В качестве подтверждения сошлемся на результаты выполненного на ЭВМ расчета горения однородной смеси в пограничном слое IJI. 82].
|
Рис. 1-4. Распределение плотности потока импульса, избыточной температуры и скорости при ламинарном горении неперемешанных газов (Р = 4,0). |



 13 августа, 2012
13 августа, 2012  admin
admin 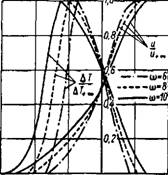
 Опубликовано в рубрике
Опубликовано в рубрике