Выполним теперь аналогичный предыдущему расчет для турбулентного высокоскоростного диффузионного факела. Для решения воспользуемся расчетом по методу подобия ры2.
|
|
Исходная система уравнений турбулентного пограничного слоя сжимаемого газа может быть записана в виде [Л. 22]
(8-13)
Эта система отличается от системы (6-1) тем, что в уравнении энергии стоит разность энтальпий торможения:
Граничные условия для рассматриваемой задачи записываются в следующем виде: ■
|
(8-14) |
|
А |
|
(8-15) |
|
»*=» + -• Са = Са. +оо ПРИ У = + ** = »J. Са = 0 ПРИ У = Уф’ |
Для динамической задачи
U = U+m при у = + СО,
|
|
Для области топлива и продуктов сгорания
Для области окислителя и продуктов сгорания
1сб = сб-оо приг/ = —оо,
— А (8-16)
1 = 1ф’ сб =0 ПРИ У = Уф — j
Для автомодельного решения примем (при ср = const):
VY" Уй:
Где ср = ср — f <р0, ср = у/ах, ф0 = const, а также
К = k„U, х, а — knU, х, D = kU, х.
Т и + оо ‘ т д +оо ‘ т Д
В результате приходим к той же, что и в § 6-1, системе обыкновенных дифференциальных уравнений (6-5).
Поскольку уравнения и граничные условия для функций F, бил имеют тот же вид, что и в задаче для М 1, тождественными будут также и решения для соответствующих величин. Отличие, как уже отмечалось, состоит в том, что в приведенные выше уравнения и решения везде входит энтальпия заторможенного газа І* — срТ* вместо і = срТ в случае М 1 •
Для расчета профилей скорости, термодинамической температуры, температуры торможения и концентраций необходимо знать местоположение фронта пламени и закон изменения плотности в поперечных сечениях пограничного слоя. Этот закон может быть определен из выражения для распределения температуры торможения путем алгебраических преобразований. Покажем это на примере для области топлива, для которой
|
V- |
|
■Т. |
|
(Ф) |
Ф. _ і / р+
|
Или Где |
Та~тФаФ____ — в. <7гл 1 / 1+1
Т, а, — Т. а.
+ оо +оо ф ф
,^1+iziM?, М? = М2+„[/(ф)]2. (8-18)
С учетом уравнения состояния придадим выражению (8-17) вид
—Ft = о,
|
+ |
А I а
Откуда следует
©і (Ф)
_______________________
Аналогичным путем получим выражение для Т^рф/р для области окислителя:
|
1 |
|
4 |
|
УіІ |
|
РФ Р |
|
|(ф) |
|
+ |
|
+ |
— а, о),. ■
Перейдем теперь к определению местоположения фронта пламени. Для этого, используя обычное для диффузионного факела условие (6-4), получаем в окончательном виде равенство
|
2ш, |
|
Яф 1 + erf (<Рф V®т) |
|
(v°n + |
[1 _ erf (фф У"ат
— 1
•ехр [_ф2ф(1_ат)]=2>±^
1 + erf (ч=ф) L ‘"J сб,-°
|
____ аф |
Которое при М да 0 (когда а = 1) принимает более простой вид:
|
У"! ("II +1) |
|
— і/ 1-Е |
|
А, + |
|
Р =2 |
|
2(о, |
|
1 + 1 |
Erf (ффУЧ)
Из этого соотношения видно, что увеличение степени перегрева (т. е. повышение теплотворности топлива) приводит к смещению фронта пламени к внешней границе пограничного слоя. Аналогичный результат был получен ранее при решении задачи о горении в ламинарном пограничном слое. Качественное соответствие результатов расчета турбулентного факела, основанного на использовании расчетной схемы подобия ры2, с решением физически строгих уравнений ламинарного движения подтверждает целесообразность применения этой схемы к расчету турбулентного факела.
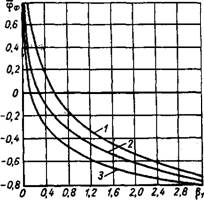
Обратимся теперь к анализу влияния числа М+оо на аэродинамику диффузионного факела. На рис. 8-5 показаны зависимости Фф = / (pi), рассчитанные для различных значений числа М+оо. Из этого графика видно, что характер зависимости координаты
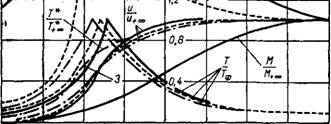
Фронта горения от стехиометрического комплекса (3 при различных значениях М+во остается одинаковым. Однако с увеличением скорости набегающего потока (при прочих равных условиях) фронт пламени смещается к внешней границе пограничного слоя. На рис. 8-6 приведены расчетные профили термодинамической температуры, температуры торможения, скорости и числа М в пограничном слое при наличии фронта пламени. Из графика видно, что изменение М при-
Рис. 8-5. Зависимость фф = / (Pi) в турбулентном пограничном слое
|
|
1 — при М+ос = 0; 2 — при М+00 = 5; 3 — при М+00 = 10 (6^ = <а2 = 10).
Водит к заметной перестройке температурных и скоростных полей. Однако даже значительное изменение числа М не вызывает существенной деформации поля скорости. Качественное тол-
|
|
|
-1,2 -0,8 -0,4 0 OA 0,8 1,2 Рис. 8-6. Распределение скорости, числа М, термодинамической температуры и температуры торможения в турбулентном пограничном слое. / —при М+00 = 0; 2 — при М+00 = 5; 3 — при M+ot) = 10 (<о = — <0j = 10, = 2,2). |
Кование этих кривых остается тем же и для ламинарного факела. Сохраняется в принципе и возможность обобщения расчета на случай истечения газа с недорасширением.



 13 августа, 2012
13 августа, 2012  admin
admin 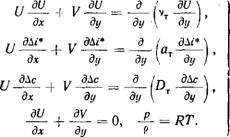
 Опубликовано в рубрике
Опубликовано в рубрике