Как отмечалось, прямым путем расчета факела, как и других случаев горения в потоке газа, было бы интегрирование основных уравнений, содержащих распределенные в объеме источники. Этот путь в виде аналитического решения задачи и даже численного расчета на ЭВМ весьма затруднителен из-за нелинейности основной системы дифференциальных уравнений (движения, энергии и диффузии) и наличия существенно нелинейных источников тепла и вещества. Более того, отсутствие в настоящее время достаточных сведений о закономерностях турбулентного переноса и кинетики реакций в пламенах (не говоря уже об общей незамкнутости системы уравнений Рейнольдса для сжимаемого газа) существенно снижает эффективность численных расчетов. Наряду с этим со значительными трудностями сопряжено и прямое экспериментальное исследование процесса горения в потоке газа и, в частности, исследование турбулентного газового факела.
В этих условиях роль эффективного вспомогательного средства исследования могло бы сыграть электромоделирование [Л. 311, проведенное с сохранением основного в физической обстановке явления — аэродинамической структуры турбулентного потока и, в частности, влияния ее на макрокинетику процесса. Сущность моделирования сводится к имитации тепловыделения за счет горения с помощью джоулева тепла, выделяющегося при прохождении через разогретый газ электрического тока.
Математическим основанием для такой аналогии является общность температурной зависимости скорости реакций (закон Аррени- уса), с одной стороны, и электропроводности низкотемпературной плазмы, с другой. Для обоих явлений эту закономерность принято выражать в виде экспоненциальной зависимости от температуры:
А = ехр(-А.) и І_вехр
Где в дополнение к принятым ранее обозначениям введены новые: А1 и А 2 — соответственно величины, пропорциональные энергии активации для химической реакции и ионизации.
Существенно, что речь идет не только об одинаковом характере • зависимости — резком возрастании величин k и а с повышением температуры, но и о близости значений и Л2 по порядку величины. Некоторые типичные значения А1 и Л2 (для р — 1 атм) указаны в табл. 10-1.
Таблица 10-1
|
Вид плазмы |
Ионизирующая присадка(калий или цезий), % |
Л3, эв |
Ли эв, для углеводородных топлив |
|
Воздух Продукты сгорания » » Аргон |
0-1 (К) 0,02—0,04 (К) 0,02 (Zs) |
2,24—расчет [Л. 107] 2,24—опыт [Л. 112] 1,94—расчет ]Л. 115] 1,63—расчет [Л. 115] |
1,6—2,4 |
Аналогичный характер ряда эффектов (гистерезис и др.) при горении и при прохождении электрического тока через полупроводник, основанных на единой по виду температурной зависимости скорости реакции и сопротивления, отмечался ранее [Л. 29]. В рассматриваемой задаче, однако, речь идет о, вероятно, значительно более эффективном и, что особенно важно, близком к натурным условиям методе моделирования.
При обсуждении принципиальной возможности моделирования ограничимся следующими допущениями. Будем считать электрические токи, проходящие через низкотемпературную плазму, достаточно малыми, так что воздействие их на течение сведется к одному только тепловыделению. Этому случаю отвечает отсутствие магнитного поля, как приложенного, так и индуцированного, вследствие малости магнитного числа Рейнольдса (ReM < 1). При соблюдении этого условия система дифференциальных уравнений движения и энергии для потока реагирующей газовой смеси и потока низкотемпературной плазмы, по которой протекает ток, при определенных условиях будет аналогичной. Действительно,
Уравнения движения и неразрывности для вязкого сжимаемого газа в обоих случаях будут полностью совпадать. В уравнение энергии взамен удельного тепловыделения за счет химической реакции войдет джоулево тепло. Тождественным будет также уравнение состояния (идеального газа).
Для уравнения диффузии, входящего в систему уравнений, описывающих процесс горения, на плазменной модели не будет аналога. Для сохранения общности процессов и возможности приближенного моделирования следует обеспечить такой характер зависимости локального тока от сопротивления, который имитировал бы в конечном счете эффект выгорания горючей смеси. Иначе говоря, следует обеспечить температурную зависимость джоу — лева тепла, выделяющегося в плазме, аналогичную зависимости скорости тепловыделения при реакции от температуры. Для сильно экзотермических реакций эта зависимость (рис. 10-1) обладает следующими характерными свойствами: резким, практически экспоненциальным подъемом ) в области, близкой к воспламенению (интенсивным выгоранием — выделением тепла — вблизи максимальной температуры) и весьма крутым последующим спадом к нулю вследствие выгорания реагирующих компонентов. Поэтому простейшей качественно достоверной аппроксимацией этой зависи — Рис 1(И 3авнсимость мости на электрогазодинамической модели скорости реакции горе — будет введение ограничения тока и выклю — иия от температуры, чение его при достижении заданной максимальной величины.
Подобие граничных условий — необходимое условие моделирования — будет осуществляться автоматически путем выбора соответствующей геометрически подобной схемы модели, распределения горячих и холодных потоков и т. д.
Наиболее просто осуществить аналогию на плоском течении, пропуская электрический ток через поток плазмы (продуктов сгорания или, например, разогретого инертного газа с легко ионизируемыми добавками) нормально к плоскости вектора скорости. Для осесимметричного движения осуществление моделирования, хотя принципиально и не исключено, сопряжено с рядом трудностей и здесь не рассматривается.
|
|
Обратимся к некоторым примерам, иллюстрирующим предлагаемый метод моделирования. Ограничимся при этом вначале только принципиальными соображениями. В качестве первого простейшего примера рассмотрим задачу о воспламенении в турбулентном потоке однородной горючей смеси, движущейся вдоль пластины. Рассмотрим температурное поле до воспламенения (включительно),
Т. е. пренебрежем выгоранием смеси. В этом случае взамен третьего
Уравнения системы
|
+ рт |
|
Ри |
Ди
Ди __ дхт др и dpv ________ q
|
Дх |
|
(10-1) |
Ду ду дх ду
ДТ, дТ. п? UCp~lh [>VCp "ду’ CieXP
Где Сх = * яа ch (Г A JT2) для случая Г < Т (см. § 5-3), в общем случае х = k (T)/k (Г), будем иметь на модели (рис. 10-2)
При прохождении тока через плазму уравнение
ДТ. дТ Р ис,— + рср— =
• (10-2)
В уравнениях (10-1) и (10-2) тт и qT — соответственно касательное напряжение турбулентного трения И’ поток тепла, выражения Q X X ехр (—AJT) представляют собой соответственно тепловыделение за счет химической реакции и джоу — лево тепло, С2 = const (У2//2), V — приложенное извне постоянное напряжение, I — расстояние. между электродами на модели.
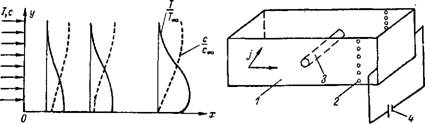
Характер температурного поля, отвечающего воспламенению, схематически показан на рис. 10-3 (аналогичные профили температуры, определенные численным расчетом, приведены в работе [Л. 83]).
|
Поненте в виде А 2 (Гм |
Для того чтобы в той же задаче учесть в первом приближении выгорание, для условий подобия полей температуры и концентраций следует, как указывалось выше, принять множитель при экс-
Т) •(Гмакс—максимальное значение
Температуры) или, что практически удобнее, А2 (/„аКс — /)> т — е. ввести на модели выключение тока при достижении максимального значения аналогично прекращению тепловыделения при достижении максимальной температуры Т = Гмакс.
|
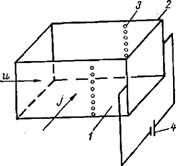
Рис. 10-2. Схема моделирования зажигания при продольном обтекании накаленной поверхности. 1 — пластина; 2 — электроды; 3 — измерительные электроды; 4 — источник питания. |
На рис. 10-4 показана схема моделирования стабилизации пламени в плоском гомогенном турбулентном факеле за плохо обте-1 каемым телом. Как и в предыдущем примере, здесь сохраняются? без изменения условия движения (осредненного и пульсационного): и «автоматически» воспроизводится уравнение энергии и его взаи-: мосвязь с движением. Соблюдаются, очевидно, и граничные уело-.
Вия для скорости и температуры. Рассмотренная аналогия относится к случаю, когда число Льюиса Le = a/D близко к единице, что достаточно точно выполняется в развитом турбулентном потоке.
Заметим также, что, используя плазму в качестве своеобразного термометра сопротивления, можно моделировать протекание процесса смешения в потоках сжимаемого газа. В этом случае, представляющем самостоятельный интерес, значение тока должно быть, очевидно, минимальным, обеспечивающим измерение, а выделяемое током тепло — пренебрежимо малым.
При практическом осуществлении электромоделирования процесса горения встретятся неизбежные трудности. В частности, по-
|
Рис. 10-4. Схема моделирования стабилизации пламени за плохо Обтекаемым телом. / — электроды; 2 — измерительные электроды; 3 — плохо обтекаемое тело; 4 — источник питания. |
|
Рис. 10-3. Распределение температуры и концентрации в пограничном слое при обтекании накаленной поверхности потоком реагирующего газа. |
Требуется, по-видимому, избавиться от искажений, связанных с при — электродным падением потенциала, и др. Предварительные данные показывают, что эти трудности могут быть преодолены. Наряду с этим желательна предварительная экспериментальная проверка основного в методе — возможности выявления в опытах влияния турбулентных пульсаций температуры на макроскопическую кинетику реакции. Этот вопрос может быть легче всего решен тем же методом электромоделирования при изучении влияния пульсаций на электропроводность низкотемпературной плазмы.



 13 августа, 2012
13 августа, 2012  admin
admin 
 Опубликовано в рубрике
Опубликовано в рубрике