Для выяснения основных закономерностей развития прямо — струйного затопленного диффузионного турбулентного факела и сопоставления результатов расчета с экспериментальными данными была исследована аэродинамическая структура газового факела [Л. 44]. Опыты проводились на трех различных установках, от­личающихся друг от друга размерами. Во всех случаях газ вытекал Из профилированного сопла с сильным поджатием. Это обеспечи­вало получение практически равномерного профиля ри2 и темпера­туры на выходе из горелки и постоянство давления во всем поле течения факела. В качестве топлива на установке № 1 применялась смесь бутана с пропаном, на установке № 2 — та же смесь, балла­стированная продуктами сгорания этого же газа в воздухе, на уста­новке № 3 — смесь паров бензина с продуктами сгорания, полу­ченными при предварительном сжигании бензина с воздухом. Ос­новные характеристики режима работы установок представлены в табл. 3-1.

В опытах проводились визуальное и фотографическое (включая стереофотосъемку) наблюдения внешнего вида факела и подробное измерение профилей температуры и динамического давления ри2 в сечениях факела, расположенных на различном расстоянии от

Среза сопла. Измерение ри2 осуществлялось с помощью трубок Пито, выполненных из кварца. Температура измерялась платино — платинородиевыми термопарами со спаем диаметром около 0,3 мм и проволокой диаметром 0,2 мм. В показания термопар вводилась поправка на излучение, величина этой поправки не превышала Е—7%. Каждый режИм повторялся несколько раз. Воспроизво­димость результатов была вполне удовлетворительной.

Приведем вначале некоторые данные визуальных наблюдений. На рис. 3-1 показана фотография факела, полученного на уста­новке № 2. Из фотографии видно, что турбулентный факел можно условно разделить на две характерные области, существенно раз­личные по внешнему виду и состоянию зоны горения. В первой из этих областей, расположенной вблизи сопла, диффузионный факел образует гладкую ламинарноподобную поверхность, весьма устойчивую к различного рода возмущениям. На некотором рас­стоянии от среза сопла (порядка 2—3 калибров) происходит за­метный распад этой поверхности. При этом размеры зоны, в ко­торой завершается переход к полностью турбулентному режиму, сравнительно малы и не превышают одного калибра. Основная часть факела, лежащая за зоной распада, имеет размытые контуры. Аналогичная картина горения диффузионного факела была ранее описана в ряде работ [Л. 91 и др.].

Наиболее подробно процесс распада присоплового пламени был рассмотрен Хоттелем и Гаусорном [Л. 33] при исследовании пере­хода ламинарного горения в турбулентное. Экспериментами этих авторов было показано, что при определенном значении числа Рейнольдса истекающей струи в вершине факела появляются пуль­сации, приводящие к разрушению ламинарного фронта. По мере увеличения значения числа Re тичка, в которой начинаются воз­мущения факела, перемещается по направлению к соплу, однако дальнейшее увеличение скорости истечения практически не ска­зывается на положении этой точки Интересно отметить, что пои больших значеннях числа Re длина ламинарной части факела практически не зависит от рода газа

Аналогичные результаты были получены в работе Ш. 96], в ко­торой приводятся фотографии этиленового факела и сравниваются с аналогичными фотографиями негорящнх струй этилена в воздухе.

Рис. 3-1. Фотография турбулентного диффузной ного факела.

Оказалось, что в негорящей струе наблюдается гладкий участок до заметной турбулизапии, происходящей на некотором расстоя­нии от сопла.

На рис. 3-2 приведены результаты этих экспериментов в виде зависимости hTldn = / (Ren), где hT — расстояние от устья сопла до начала видимой гурб>лизации струи, Re„ u0djv. Из графика видно, что в негорящем потоке место видимого распада струи при прочих равных условиях находится на более близком расстоянии от среза сопла, чем в факеле Последнее, по мнению авторов ра­боты [Л. 96], объясняется тем, что выделение тепта (точнее, повы­шение вязкости в связи с ростом температуры) оказывает стабили­зирующее действие на поток. По существу к аналогичным выводам прпходят и авторы работ [Л. 33, 92], также допускающие возмож­ность существования в турбулентном факеле начальной зоны ла­
минарного горения, даже в тех случаях, когда поток на выходе из соплі полностью турбули. їован. Это мнение встречается в ряде работ |«71. 14; 20 и др.], однако подробные данные о структуре присоплового участка струи и, особенно, факела в настоящее время отсутствуют.

Следует отметить некоторую противоречивость в толковании результатов упомянутых выше работ, допускающих и другую трактовку. Действительно, независимость длины участка пламени до возмущения (в области сравнительно больших значений числа Рейнольдса) от скорости истечения и от физических констант газа говорит скорее не о ламинарном, а о турбулентном режиме тече­ния (и горения) на этом участке. В связи с этим была предпринята попытка непосредственного иссле­дования структуры присоплового пламени. Для этой цели было про­ведено качественное изучение пуль­саций температуры в различных точках начального участка факела.

Пульсации температуры изме­рялись с помощью насадка элек — тротермоанемометра, снабженного платиновой нитью диаметром 20 мк. Насадок работал в режиме термо­метра сопротивления. Изменения напряжения на концах нити пода­вались на вход усилителя ЭТАМ-ЗА и затем регистрировались па экране катодного осциллографа. Опыты показали, что в начальном участке диффузионного факела суще­ствуют довольно значительные систематические пульсации темпе­ратуры. Все это свидетельствует о необходимости дальнейшего изучения режима течения в этой области.

На рис. 3-3 приведена серия стереоскопических фотографий, дающих некоторое представление о мгновенной структуре турбу­лентного факела. Для сравнения на рис. 3-4 показаны обычные фотографии такого же факела (установка № 1), снятые с различ­ными экспозициями. Из стереофотографий, рассматривая их через стереоскоп, можно видеть, что в исследованных условиях горение протекает на определенных поверхностях — фронтах пламени, сложным образом распределенных внутри зоны горения. Интересно отметить, что в некоторых случаях возникающие в факеле элемен­тарные фронты располагаются концентрически относительно друг друга. Эти наблюдения, как и результаты работы [Л. 74], говорят в пользу модели поверхностного механизма горения в турбулент­ном потоке.

Перейдем к рассмотрению опытных данных по распределению плотности потока импульса ры2 и температуры в поперечных

Сечениях диффузионного факела. На рис. 3-5 представлены опытные данные по распределению плотности потока импульса в поперечных сечениях основного и начального участков турбулент­ного факела, полученные на установке № 3. Как видно из графиков, в автомодельных участках турбулентного диффузионного факела, как и в струях, наблюдается универсальность профилей ры2.

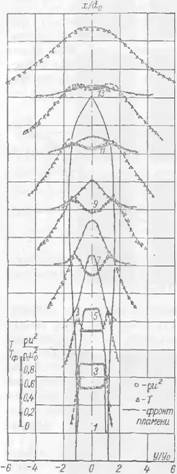
Общая аэродинамическая картина затопленного газового фа­кела показана на рис. 3-6. Этот график дает наглядное представ­ление о характере скоростных и температурных полей. Как видно из этих данных, на оси факела происходит монотонный рост темпе­ратуры от ее начального значения на выходе из сопла до некото­рого максимального значения,[13] соответствующего температуре го-

Щ

1,2

Рис. 3-5. Универсальные профили плотности потока импульса в поперечных сечениях турбулентного диффузионного факела (U — fpи2): а — начальный участок; б — основной участок.

Рения. За зоной горения происходит падение температуры вследст­вие смешения горячих продуктов сгорания с окружающим возду­хом. Как видно из рис. 3-6, по мере удаления от сопла происходит выравнивание температурного поля в поперечных сечениях факела. Однако, даже на значительных расстояниях от сопла, в пределах существования фронта пламени профили температуры имеют два отчетливо выраженных максимума, свидетельствующих о наличии сравнительно узкой зоны, в которой протекает интенсивная ре­акция. Ширина этой зоны, как видно из распределения темпера­туры, нарастает по мере удаления от устья факела.

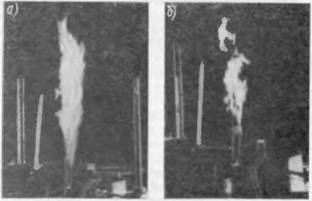
Существенный интерес представляет вопрос о влиянии началь­ной концентрации газа (и пропорциональной ей величины тепло­творности истекающей смеси) на структуру и размеры диффузион­ного факела. Некоторые данные, характеризующие это влияние, приведены на рис. 3-7 и 3-8. Из фотографий и графика видно, что увеличение концентрации топлива в исходной смеси приводит к
удлинению и расширению факела (см. рис 3-15) и к замедленному росгу температур..! п,) оси факела.

По данным ряда нссчедователен [Л. 20; 33; 41 и др I. длина турбулентного факела и его форма практически не зависят от на­чальной скорости истечения газа. В качестве примера можно ука­зать на приведенный выше рис. 1-5, заимствованный из работы [Л 33 ]. J» гверждения, содержащиеся в ра­ботах [Л. 58; 97], о зависимости длины турбулентного факела от ско ростн истечения, по-видимому, объ­ясняются недостатками эксперимен­та, в частности неточностью ви зуального определения длины фа кела Опыт показывает, что конец факела, достаточно четко определяе­мый по максимуму температуры на

Рис. 3-7. Фотографии турбулентного диффузионного факела: а—при сс0 = 0 055 кг/кг; б — пр». сао— 0,085кг/кг; в — при саи = 0 12 кг! кг.

Оси, не совпадает с концом светящейся зоны. Независимость длины факела от скорости вытекает из приведенного в § 2-3 расчета. Последний указывает на согласующуюся с опытом и соображе­ниями размерности пропорциональность длины факела диаметру

Сопла (lid = const), а также параметру т. е., в част­ности, начальной концен­трации топлива.

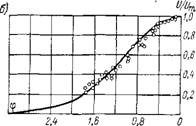
На рис. 3-9 приведены экспериментальные данные по изменению динамиче­ского давления ри2 на оси факела. Как видно из гра­фика, относительное изме­нение плотности потока импульса на оси факела не зависит от скорости исте­чения и начальной концен­трации газа и имеет такой же характер, как и в обыч­ных турбулентных струях при отсутствии горения. Это также является под­тверждением исходных по­ложений аэродинамической теории диффузионного тур­булентного факела и согла­суется качественно с ра­счетом.

Обратимся к количе­ственному сопоставлению результатов расчета и опыта.

На основе опытных дан­ных по изменению дина­мического давления вдоль оси факела, полученных на установке № 2, была опре­делена зависимость эффек­тивной координаты ]/ —

= f(x), показанная на рис. 3-10. Как видно из графика, в турбулентном диффузионном факеле эта зависимость имеет такой же характер, как и в газовой струе без горения [Л. 22]. При этом для затопленного факела в автомодельной об­ласти течения величина 1 Е является практически ли-

Нейной функцией продольной координаты х. Значение коэффи­циента пропорциональности С в формуле }/~ і = Сх по данным опытов на этой и других установках оказалось равным С 0,039-^- 0,043. В качестве среднего значения, как и для расчета струй, можно принять С яа 0,04.

По экспериментальной зависимости ]/"Г= /(х) сопоставлялись результаты расчета, выполненного по методу эквивалентной задачи теории теплопроводности для а = 1, с данными экспери­мента.

В качестве примера на рис. 3-11 показаны расчетные и опытные профили относительных значений ри2 в поперечных сечениях фа­кела. Наблюдается практи­чески во всех случаях хо­рошая сходимость расчет­ных и непосредственно из­меренных в эксперименте значений. Тем самым под­тверждается одно из основ­ных положений расчета — универсальность распреде­ления ри2 в факеле и струях.

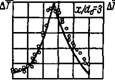
На рис. 3-12, 3-13 и 3-14 приведены данные по рас­пределению температуры. Здесь наряду с качествен­ным совпадением наблю­дается удовлетворительная сходимость количественных результатов во внутренней зоне и некоторое отклоне­ние расчета от опытных данных во внешней зоне факела. Заметно также, что по мере удаления от устья факела максимум темпера­туры становится более пологим, а зона максимальной темпера­туры расширяется. Этим и прежде всего тем, что в расчете не учтено различие в интенсивности переноса импульса и тепла (т. е. нера­венство ст < 1), следует объяснить наблюдаемые расхождения опытных и расчетных данных.

Расчетные очертания фронта пламени для трех различных зна­чений начальной концентрации топлива изображены на рис. 3-15. На графике также нанесены экспериментальные точки (по макси­муму температуры). Как видно из рисунка, совпадение расчета с опытом достаточно хорошее: расхождение в длине факела не пре­вышает 10—15%, т. е.. близко к пределам точности измерений.

Для сравнения на рис. 3-15 для одного из примеров (со0 = = 0,12 кг/кг) нанесена также линия фронта пламени, рассчитан­ная по холодному смешению (из условия ст = 1 при ос = 1) по фор-

Как видно из графика, результаты такого расчета резко отли­чаются от опытных. Поэтому предположение о совпадении фронта пламени со стехиометрической поверхностью (при смешении без горения), встречающееся в некоторых работах ІЛ. 93; 106], не­пригодно для количественного расчета.

Результаты сопоставления, как следует из приведенных дан­ных, свидетельствуют об эффективности приближенного метода расчета и, в частности, о том, что сделанные в расчете допущения не вносят существенных искажений. Такой расчет позволяет опреде-

Лить с точностью 10—15% длину факела, конфигурацию фронта пламени и, наконец, профили основных переменных. Тем самым подтверждается целесообразность использования расчетного ме­тода эквивалентной задачи (при ст = 1) для приближенного ин­женерного расчета факела.

При дальнейшем развитии расчета и эксперимента можно будет учесть действительное значение ст и прийти к лучшему согласию результатов расчета и опытов.